基于LFMCW 雷达测距的空中目标轨迹测量方法

牛龙飞

（1.国防大学联合勤务学院，北京 100858；2.解放军92493 部队，辽宁 葫芦岛 125001）

0 引言

在海军舰空导弹试验中，导弹的命中精度一直是试验考核的重点和难点，脱靶量则是考核舰空导弹命中精度的一项重要参数，矢量脱靶量不仅能够获取标量脱靶量，还能获得导弹与靶标遭遇过程的相对运动轨迹和相对速度矢量。对于装备试验鉴定来说，获得矢量脱靶量对舰空导弹试验考核来说更具意义。如果能够实现弹靶遭遇过程中导弹与靶标的实时定位，得到导弹与靶标的空中轨迹，导弹与靶标的矢量脱靶量自然能够通过计算获得，那么矢量脱靶量测量问题就可以转化为空中目标轨迹测量问题。当前，空中目标轨迹测量分为协同式和非协同式两种工作方式。协同式测量距离远、精度高，缺点是需要在导弹上加装合作装置；非协同式测量系统受导弹目标特性影响较大，测量距离和精度不如协同式测量系统。随着科技发展，协同式工作方式的合作装置体积越来越小，重量越来越轻，对被加装的导弹飞行影响很小。因此，采用该种工作方式测量空中目标轨迹的机会大大增加。

LFMCW 雷达以其具有的较高距离分辨力、无距离盲区、尺寸小、重量轻、功耗小、成本低等优点，而被广泛应用。本文基于以上考虑，提出利用LFMCW 雷达，采取协同式工作方式对导弹和靶标加装合作装置，通过多基站雷达测距实现空中目标轨迹测量，并对此种方法测量精度进行推导计算，利用仿真手段验证其用于空中目标轨迹测量的可行性。

1 LFMCW 雷达测距精度分析

根据靶场开展舰空导弹试验的实际测量需求，测量目标最大距离不小于60 km，综合考虑测量指标要求、海上复杂环境和工程设计可实现性，雷达采用X 波段，理由参见文献［7］。信号处理方法采用对称三角波LFMCW 双差拍-傅里叶变换处理方法。

1.1 双差拍-傅立叶变换处理方法原理

假设三角波线性调频连续波信号上、下调频时长均为T，那么信号的重复周期T=2 T。因三角波线性调频连续波信号的周期重复性和调频对称性，对应［-T，0］和［0，T］时间段的回波，都是分段信号。当进行混频处理时，与发射信号调频斜率相同的部分是传统差拍-傅立叶处理中的有效信号；与发射信号调频斜率相反的部分，对测距而言属于干扰信号。两次差拍处理中有效信号与干扰信号是相互转化的，且两者所占的比重取决于测量目标的延时参数τ，因其中至少有一次处理的有效信号能量可以达到或超过50%，所以可以采用发射信号与反发射信号分别与同一回波信号进行两次差拍- 傅立叶变换处理，通过比较两次差拍处理性能的优劣，并分析两次差拍信号的频谱，即可估计高速目标的距离与速度参数，这种处理方法称之为双差拍-傅里叶变换处理。

通过性能分析，在最差情况下，经过双差拍-傅立叶变换处理的性能要比相同参数条件下的传统差拍-傅立叶处理要低6 dB。因此，需要满足前者信噪比门限较后者高6 dB 的情况下，才能将对称三角LFMCW 信号的测距范围扩展到整个信号周期T=2 T。

不同延时区间运动目标两次差拍处理对应的谱峰频率以及相应的解耦合公式如表1 所列。

表1 不同延时区间运动目标两次差拍处理的谱峰频率及解耦合公式

1.2 测距误差分析

对采用对称三角波的LFMCW 体制雷达测距误差进行仿真分析，条件设置如下：雷达工作频率f=10 GHz，调频时长T=0.2 ms，调频带宽B=50 MHz，信号重复周期T=2 T。理想匹配滤波压缩倍数D=TB=10，对应滤波器的理论信噪比增益为40 dB。假设测量雷达输出信噪比要求为12 dB，采用传统差拍-傅立叶变换处理方法的滤波器输入信噪比需要达到-28 dB，采用双差拍-傅立叶处理情况下还需至少提高6 dB，这里设定输入端信噪比为-20 dB，满足可靠检测的信噪比要求。处理中采样频率选择为f=2 B。

图1 目标A 第1 次差拍处理结果

图2 目标A 第2 次差拍处理结果

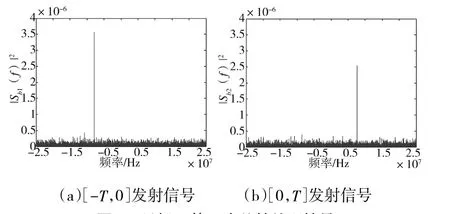
图3 目标B 第1 次差拍处理结果

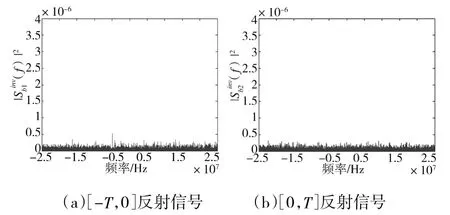
图4 目标B 第2 次差拍处理结果

对上述两个运动目标进行1 000 次蒙特卡罗仿真分析，得到距离和速度的估计精度如表2 所示。

由表2 可以看出，随着输入信噪比的提高，距离和速度估计精度都有显著提高，当输入信噪比为-10 dB 时，对50 km 外目标距离估计精度0.05 m，速度估计精度1 m/s，较高的距离和速度估计精度为下一步对高速目标进行定位奠定了良好基础。

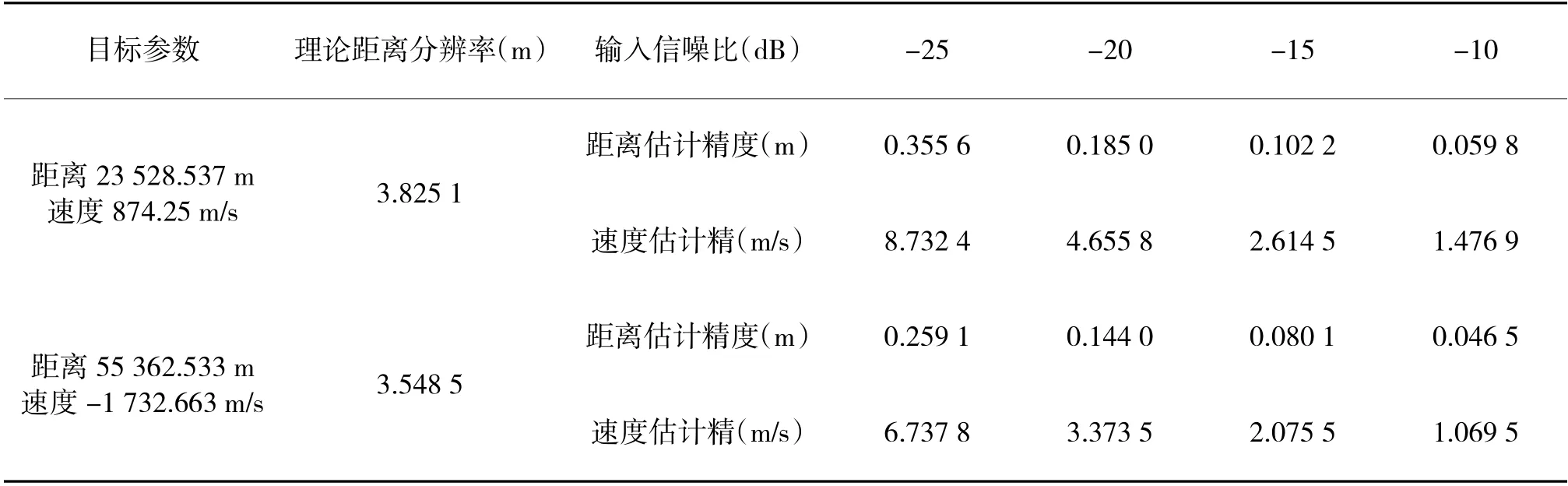
表2 不同输入信噪比下距离和速度估计精度

2 多站定位精度分析

2.1 数学模型

假如有n 个测量站分散部署在n 个位置，站址坐标是x=［xyz］，i=1，2，…，n。这些测量站只测量目标相对于站址的斜距r，这样就可以得出以站址为中心、半径为r的n 球面，这n 个球面的相交点就是目标的空间位置。

图5 给出目标位于T 的位置上，其位置矢量为x=［xyz］，而4 个测量站的站址分别为x=［xyz］，i=1，2，…，n。各测量站测得的目标距离r为：

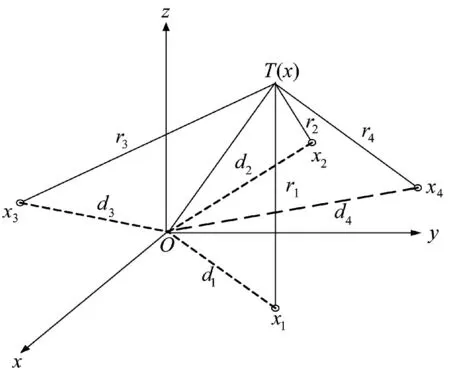
图5 斜距测量定位

x=［xyz］测量站站址是已知的，r是各测量站实际测得的目标斜距也为已知，可以列出求解目标位置矢量x 的矩阵表达式：

式中，x=［xyz］，v=［vvvvvv］。

而矩阵A 为：

2.2 多站定位误差

影响定位误差的因素主要包括3 个方面：一是与测量站数量和位置有关。由GPS 定位原理可知，要想实现空间目标定位，最少需要4 个测量站，且4个基站不能部署在同一个等高面的一条直线上。二是与测量站的时统精度有关。当前靶场时统精度可达微秒级，对定位误差影响较小，这里忽略暂不考虑。三是与测量站的测距误差有关。测量站的测距误差是影响最终定位精度的主要因素，每个测量站测距的误差可以通过对实验数据的统计处理而求得，在给定测距误差的条件下分析四站测斜距系统对目标的定位误差。已知测得的斜距是目标的位置矢量x 及站址x的函数：

对它求微分得：

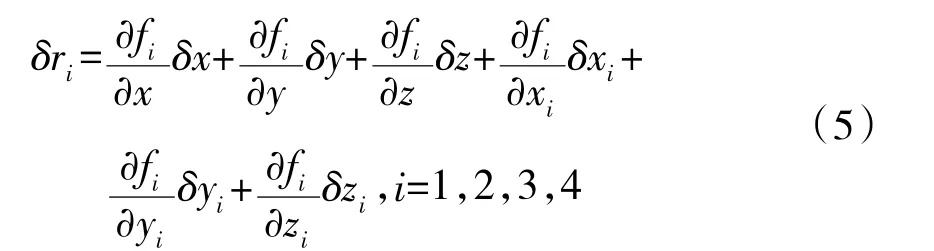
由此可见，斜距测量误差δr与目标位置误差δx=［δx δy δz］和站址误差δx=［δxδyδz］有关。由于各站的距离测量是独立的，每个站对应的测量误差之间也是互不相关的，设定距离测量误差经系统误差修正后是零均值的。由于站址坐标非常精确，误差极小，因此，在实际定位观测中站址误差可以忽略不计，所以可得出定位误差如式（6）。

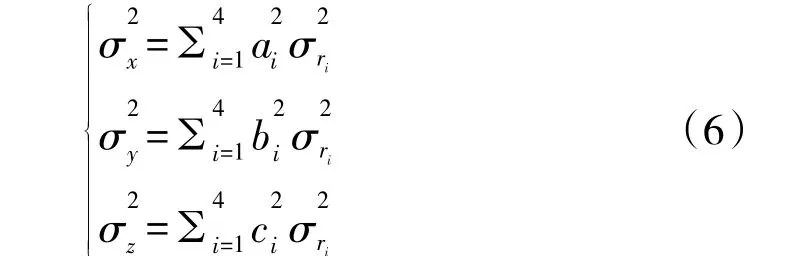
从定位误差方差公式可以看出，它与目标对应各站的方向余弦直接相关。也就是说，定位误差与目标的空间位置和测量站站址的相对几何关系有关［11-12］。

3 仿真算例

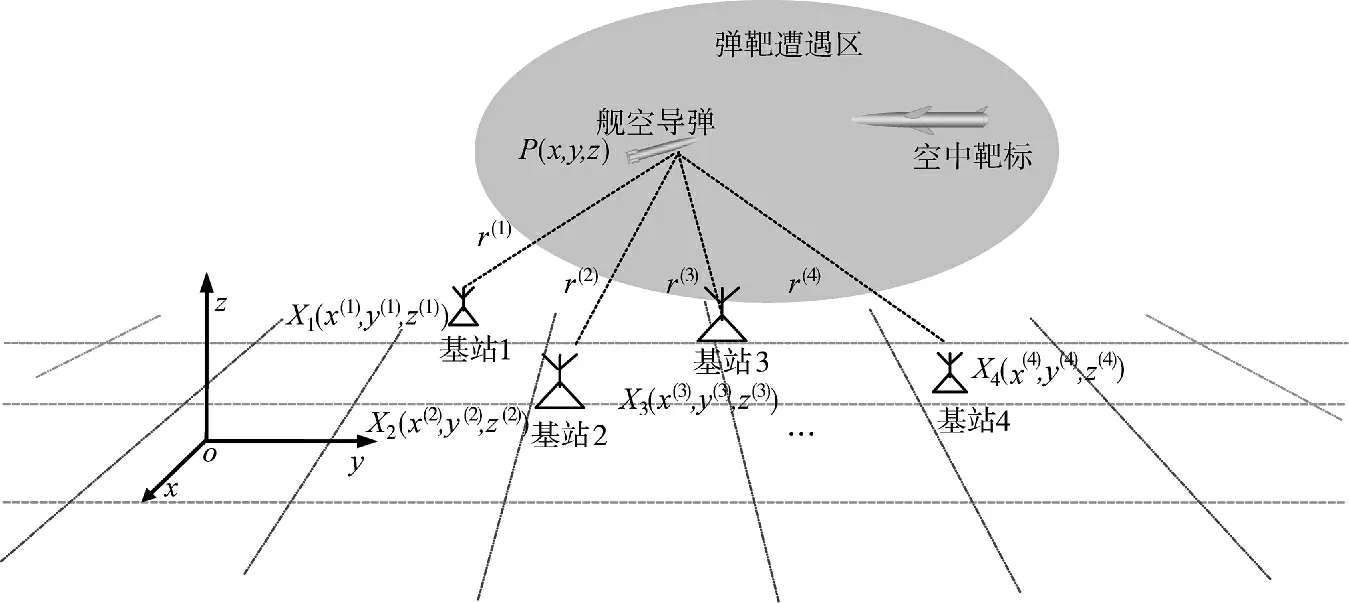
图6 观测站与目标之间的几何关系图

假设有4 座雷达测量站，在直角坐标系中，采用菱形站址布局，站址坐标分别为x=（0，5 000，50），x=（5 000，0，78），x=（5 000，10 000，500），x=（10 000，5 000，68），4 座雷达测量站对空中目标的距离测量值分别为r，r，r，r，利用LFMCW 雷达体制测距，仿真中设置不同的雷达测距误差。基于以上条件，用四基站定位系统对空中任意方位的飞行目标进行定位，根据结果分析误差和定位精度。在仿真过程中，基站x的高度坐标可调，针对中高和中低空目标，进行500 次计算统计得结果如表3，表4 所示。

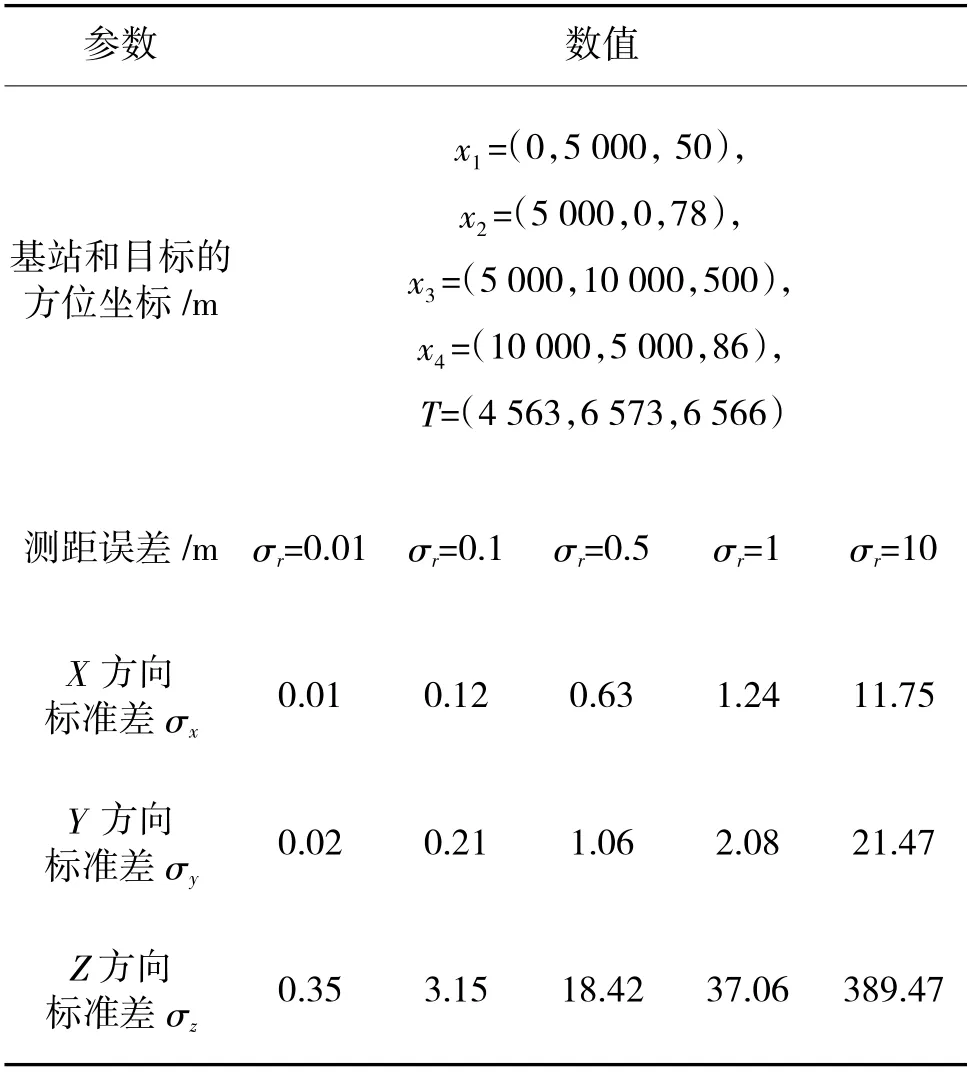
表3 中高空目标

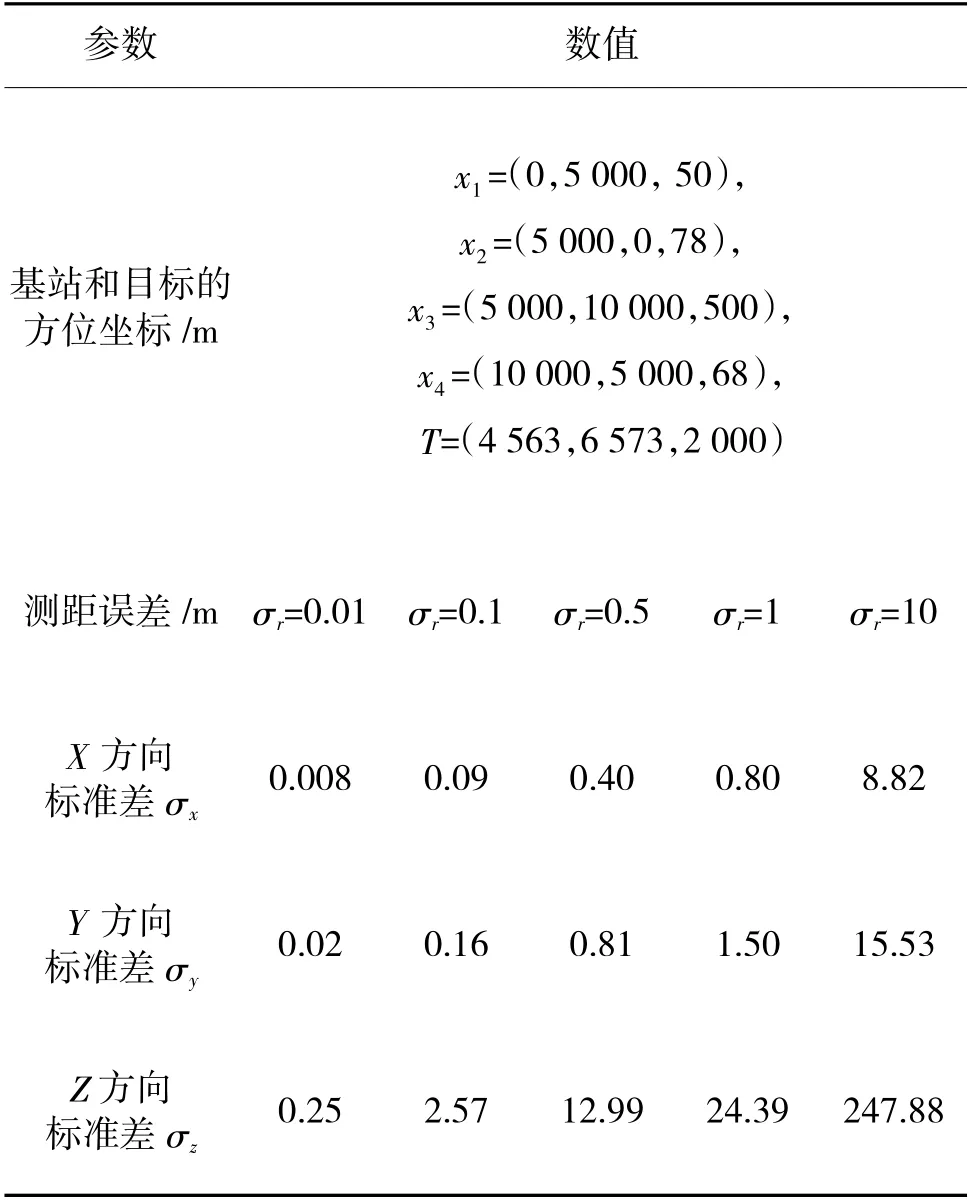
表4 中低空目标

给定4 座基站和空中目标的方位坐标，分析系统在不同测距误差条件下的定位精度（测距误差服从零均值高斯分布）。

上述仿真结果表明，当观测站位置固定时，无论哪个高度上的目标，其定位精度均与观测站测距误差相关，测距误差越小，最终定位精度也就越高。在雷达测距误差为0.01 m 时，目标在3 个方向上的定位误差均在分米级，但在Z 方向上定位误差明显偏大。

4 结论

通过上述分析，可以看出利用X 波段对称三角波LFMCW 雷达，在较高输入信噪比控制下，采取协作式工作方式进行测距，能够实现对空中高速目标实时定位，进而可以实现对弹靶遭遇轨迹的测量，其测量原理可行，具有工程应用价值和前景。但在实际应用中也还有需要深入研究的问题，如雷达系统设计、系统实际测距精度、布站位置对定位精度影响等，这些问题还需进一步深入研究并通过实验验证。