一种云计算环境下的改进任务调度算法*

张思豪，田建宇，刘银良，刘经天，刘卫新

（北方自动控制技术研究所，太原 030006）

0 引言

云计算已经成为当前大规模和复杂计算的最突出的架构。它只需最少的管理工作和信息交互，便能够完成对共享资源的按需网络访问，快速地提供和释放访问资源。随着数以百万计的用户向云系统提交计算任务，任务调度机制在其中的作用越发显著。

任务调度是指将一组任务分配给可用虚拟机的技术。任务调度机制的主要作用是在不影响服务质量的情况下提高资源利用率。任务调度算法分为两种：确定性算法和元启发式算法。

确定性调度算法包括先来先服务调度算法（first come first served，FCFS）、轮询算法（round robin，RR）、短进程优先算法（shortest job first，SJF）和慢速资源负载均衡算法（load balance over slow resources，LBSR）等传统调度算法。确定性算法是任务调度中常见的基本算法。

元启发算法包括爬山（hill climbing，HC）、模拟退火（simulated annealing，SA）、禁忌搜索（tabu search，TS）、蚁群优化（ant colony optimization，ACO）、布谷鸟搜索（cuck searc，CS）和粒子群优化（particle swarm optimizatio，PSO）等算法。这些算法的作用在于寻找一个近似解，当使用确定性算法无法获得精确的解决方案时，寻求近似解的方式将会大大提高工作效率。

粒子群优化算法是元启发算法中最常用的求解最优问题的算法之一。但是，使用该算法调度大量任务会降低系统性能。本文在粒子群算法的基础上，通过改进提出一种新的调度算法，在不影响系统性能的前提下对大量任务进行调度。它以均衡、动态的方式将提交的任务划分为多个批次。该算法主要考虑两个参数：任务的数量和每批任务的总长度。

1 云计算环境下的任务调度

任务调度是一个将传入任务分配给可用资源的进程。任务调度算法的主要目标是在不影响云的服务参数情况下最大化资源利用率。图1 显示了在云环境中完成基本调度的过程。由图可知，任务调度分为3 个阶段，第1 个流程是信息提供，任务调度程序将从任务管理器中搜集信息，计算任务属性，并在资源管理器中监视现有可用资源，以便为任务进行合理的资源分配；第2 个过程是选择过程，根据资源和任务的具体参数选择目标资源。这些参数包括任务规模、任务优先级、可靠性因子、基于作业的资源消耗成本和任务的动态时间长度，然后，任务调度程序将任务分配计划发送给资源管理器；第3 个过程是任务分配过程，该过程中任务管理器会将现有任务分配给适当的资源进行处理。

图1 云计算下的任务调度

在粒子群算法中，种群中的每个成员被称为粒子，种群称为群。一个随机初始化的种群中粒子向随机选择的方向移动，每个粒子通过搜索空间，记住自己与其他例子间的最好位置。最后，在搜索过程中，所有粒子都会逐渐趋向更好的位置，直到整个种群分布到一个最优位置。但是粒子群算法会导致算法速度和方向调节能力的降低，当粒子群算法的种群和搜索空间扩大时，寻找最优解的过程会变得更加困难。

在云环境下，基于粒子群的任务调度算法的最终目的在于最小化最大完工时间和提高任务调度服务质量水平。由于粒子群算法在数据较大的情况下性能较差，研究人员为此提出了许多改进算法，这些算法包括改进的粒子群算法和混合粒子群算法。混合粒子群算法能够在调度少量任务时降低最大完工时间和标准偏差，但在提高调度性能方面并没有太多优势。针对目前改进算法的局限性，本文提出了一种新的任务调度算法——改进粒子群优化算法（improved particle swarm optimization，IPSO）。

2 改进粒子群优化算法

改进粒子群优化算法的主要目标是将大量任务优化调度到云计算环境中的可用虚拟机，并在调度中使完工时间最小化，资源利用率最大化。下页表1 为数学分析所用到的符号说明。

表1 数学分析符号说明

VM 由L 个主机组成，每个主机上存在m 个可用虚拟机。使用VM表示第i 个资源；假设云系统已经接收到n 个任务，使用T表示第j 个任务，这些任务具有不同的大小，并且彼此独立。

调度器负责为提交的n 个任务找到m 个可用虚拟机VM 的最优分配方案。分配方案矩阵P 可表示为：

分配方案矩阵由表示第j 个任务T是否分配给虚拟机VM的二进制变量组成。它可以表述如下：

IPSO 的控制结构由分批收集任务、分批调度和最终分配计划再平衡3 个阶段组成。其流程结构如图2 所示，算法的主要阶段描述如下：

图2 改进任务调度算法流程结构

2.1 阶段1：分批收集任务

在这个阶段，任务到达就绪队列。当所有的待调度任务完成排队，就会计算任务属性。

为了最大限度地利用资源，使用了一个新的参数μ 作为资源利用状态的领先指标。它是表示可用资源平均值的利用率检查的主要参考，计算如下：

采用自适应拆分方法批量收集任务。IPSO 通过式（4）来累积任务长度之和BL：

当批量收集任务的长度超出资源使用状态时，停止批量收集任务。该算法将批处理长度设定为始终小于或等于平均可用资源，可以表示为：

2.2 阶段2：分批调度

在将任务分批收集后，调度程序尝试为每批任务寻找最优分配方案，此阶段将通过任务调度算法将每批次的任务分配到相应虚拟机。

首先，粒子群算法用创建的一组随机解来对粒子群进行初始化，然后通过群体内粒子的更新迭代来搜索最优解。因此，首先对迭代T 中的粒子位置矩阵和速度矩阵进行随机初始化；其次在每次迭代中，每个粒子需要两个最优值进行更新，即个人最优值和全局最优值。此外，该过程考虑了用于控制速度的惯性权重（ω）的值。它取决于预定义的惯量权值的最大可能值（ω）和预定义的最小可能值（ω）。

在找到个人最优值和全局最优值的最佳值后，粒子以式（8）和式（9）来更新其速度和位置。

对于每个粒子分配矩阵，VM执行分配的S 任务的完成时间可以表示为：

粒子的最优位置解由适应度函数来评估，适应度函数以目标完工时间为基础，估计调度之间的效率。为了满足所提算法的主要目标，找到PSO 的最优解，适应度函数表示为式（11），使用该公式计算每个VM 的完成时间，并返回最高完成时间作为每个PSO 粒子的适应度值：

PSO 将所有粒子的最优位置更新为：

粒子群算法将对种群内的每个粒子重复上述步骤，直到达到设置的最大迭代次数。最后，粒子群算法考虑到目前为止所找到的最优解为最终解。一旦PSO 终止，则建立当前批次的次最优分配方案。IPSO 将这个次优分配计划附加到最终分配计划中。IPSO 开始对前面的步骤进行新的迭代，以找到下一批产品适当的次最优分配计划。最后，将所有次优分配方案添加到最终分配方案中。

2.3 第3 阶段：重新平衡最终分配计划

在此阶段，改进算法将在所有资源上平衡负载。此阶段的再平衡过程基于将任务从负载最重、完成时间最长的虚拟机转移到负载最轻、完成时间最短的虚拟机。在此阶段开始时，可用资源列表中包含了所有可用的虚拟机。当列表变为空时，阶段结束。重新平衡过程可以总结如下：

1）计算所有利用虚拟机的完成时间。

2）将完成时间最长的虚拟机作为负载最大的虚拟机加入可用资源列表中。在最任务重的虚拟机中，第1 个任务被认为是当前任务。

3）将完成时间最短的虚拟机设置为负载最轻的虚拟机。并将负载最重的虚拟机中的当前任务移动到负载最轻的虚拟机中。

4）如果此动作产生的最大完工时间小于之前计算的最大完工时间，则接受更改，并更新两台机器的完工时间。如果此移动产生的最大时间间隔大于先前计算的最大时间间隔，则该动作将被拒绝

5）如果当前最重的资源中有其他任务，则将下一个任务设置为当前任务，执行步骤3）。否则，将当前最重的虚拟机从可用资源列表中移除。

6）如果可用资源列表中有任何可用资源，则转到步骤2）。

7）最后当可用资源列表为空时，均衡进程停止。

2.4 改进算法的时间复杂度

IPSO 算法的复杂性是基于其3 个主要阶段来衡量的。为了找到在m 个虚拟机上分批为k 个批次的n 个任务的分配计划，算法的复杂度计算如下所示：

阶段1：（分批收集任务阶段）此阶段应用于提交到系统的n 个任务。在这个阶段，任务调度器从任务管理器和资源管理器收集信息来创建合适的批次。提交的n 个任务根据两个阈值分成k 批任务。这个阶段的复杂度是O（n）。

阶段2：（分批调度阶段）IPSO 系统提供k 个批次，可以覆盖n 个提交的任务。利用粒子群优化算法对每批数据进行调度，得到其次优解。PSO 算法的复杂度为O（n）。PSO 将这一步重复k 次，因此，这一阶段的复杂度为k*O（n）。而k 被认为是一个最小的数字，可以忽略。因此，该阶段的复杂度为O（n）。

阶段3：（重新平衡最终分配计划阶段）在这个阶段，IPSO 试图在所有m 资源上平衡负载。这个阶段的再平衡过程是基于将任务从负载最重的虚拟机移动到负载最轻的虚拟机。平衡器的复杂度是m*O（n），而m＜＜n，所以m 可以忽略，因此，该阶段的复杂度为O（n）。

IPSO 算法总复杂度为O（n+n+n）=O（n+2n）≈O（n）。因此，IPSO 算法的复杂度为O（n）。

2.5 评价指标

IPSO 的评价指标由两个性能指标来衡量，不平衡程度（DI）和负载标准差（σ）。

不均衡DI 用来衡量各虚拟机之间的不平衡度。因此，在分配时考虑DI 可以避免不平衡的虚拟机工作负载。

标准差σ 表明从平均开始调度任务存在量的变化或弥散。

3 仿真实现及结果

为了评估IPSO 的效率，实验使用CloudSim 对不同的任务调度技术进行建模和仿真。在仿真结果的基础上，分析改进算法的性能。

3.1 模拟配置

CloudSim 是一种仿真工具，可用于评估所提改进算法与其他算法的性能，并在最大完工时间、标准偏差和不平衡程度方面与其他算法的结果进行比较，实验仿真环境如表2 所示。

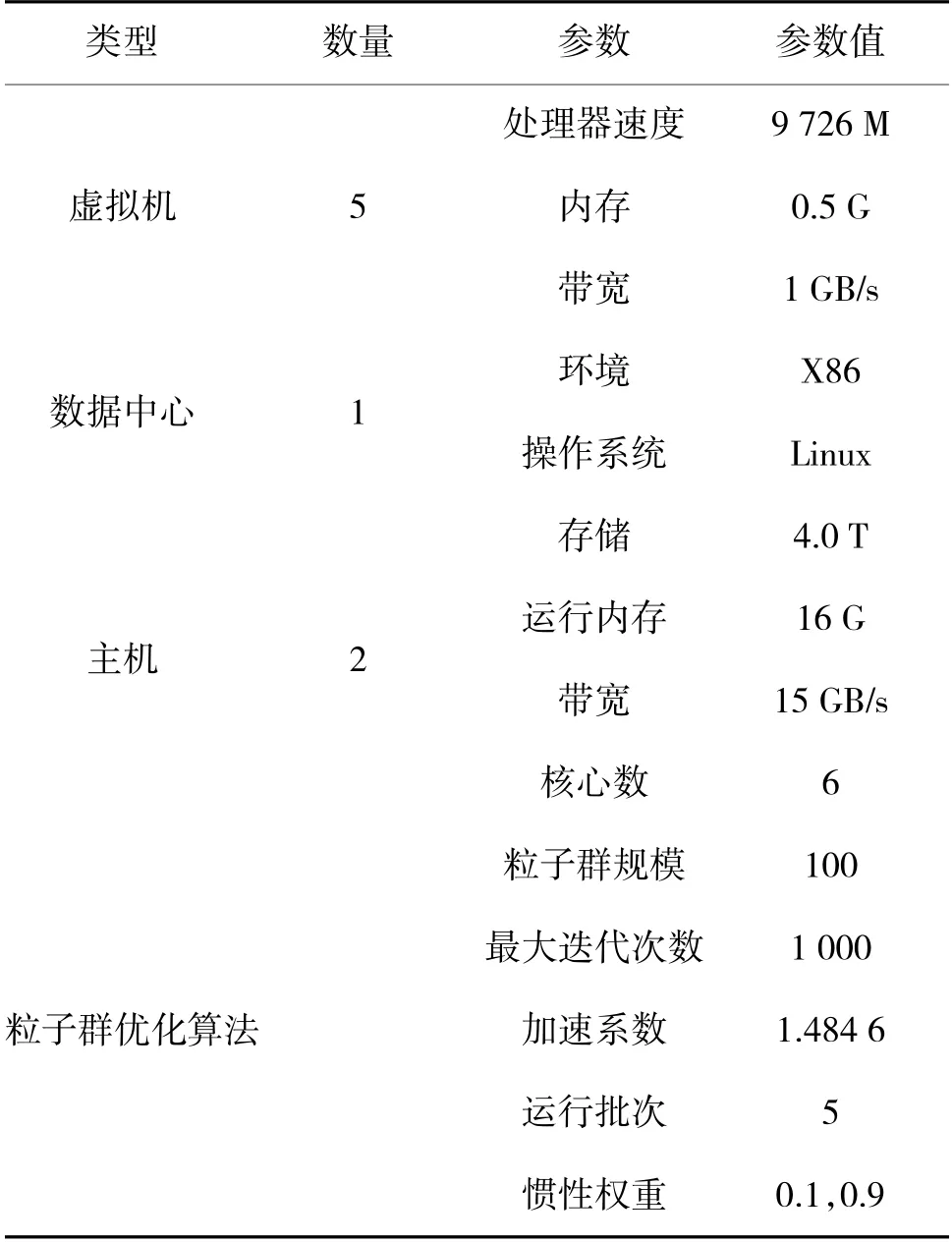
表2 实验仿真环境

3.2 仿真结果

为了评价该算法的性能，本文将改进算法与基于蚁群的任务调度算法（PSO），蚁群优化算法（ACO），蜂群算法（LBA_HB）和轮询算法（RR）4 种群算法进行了比较。

对于ACO 和LBA_HB，仿真参数是根据它们在评估中使用的实验设置来配置的。图3 显示了任务数量从3 000～10 000 变化时任务调度算法的最大时间。可以看出，与其他算法相比，IPSO 算法实现了这5 种算法中最小的完工时间。在3 000 个任务时，IPSO 的最大完工时间小于LBA_HB（25%）。当任务数量增加时，IPSO 算法的最大完工时间与其他4 种算法的最大完工时间之差也在增大。当任务数达到10 000 时，IPSO 的最大完工时间约为190 ms，而蚁群算法的完工时间约为600 ms。这间接地证明了所提算法对资源的有效利用。

图3 完成时间对比

图4 显示了被评估算法的标准差的变化。每个虚拟机完成时间的正常标准偏差是该虚拟机完成时间与所有虚拟机平均完成时间的变化。由图知，与其他4 种算法相比，所提出的IPSO 大大降低了标准差。

图4 负载标准差对比

IPSO 通过使用再平衡过程防止将请求分配给加载的虚拟机。因此，它在减少完成时间的同时有效地实现了负载均衡。在分配过程中，考虑虚拟机的不平衡程度将有助于避免虚拟机出现工作负载失衡的情况。图5 给出了RR、ACO、LBA_HB、PSO和IPSO 算法的不平衡程度。由图可知，所提出的IPSO 算法的不平衡程度最小，它可以防止失衡的工作负载情况。

图5 不平衡度对比

此外，在与其他元启发算法对比的基础上，对比文献［17-19］中所提3 种粒子群改进算法：基于吞噬双重判定的改进遗传算法任务调度（PGA_PSO）、自适应t 分布的改进粒子群任务调度算法（t-PSO）、基于混沌扰动的粒子群优化算法（NPSO）得到表3，当任务数量为7 000 时，IPSO 算法的最大完工时间相比PGA_PSO 降低了约21%，比t-PSO 降低了约33%，比NPSO 降低了约27%。当任务数量继续增加时，IPSO 算法的标准偏差显著降低。

表3 改进粒子群算法与粒子群算法的比较

4 结论

为了节约调度任务完成时间，提高集群资源利用率，实现高效的任务调度，本文提出了一种新的任务调度算法IPSO。该算法通过将大的任务列表分批处理成小的子列表，以减少每个虚拟机上的工作量。使用领先指标，在每次创建任务量时评估资源使用状态。在使用粒子群算法（PSO）为每个批次获得次最优解的基础上，改进算法（IPSO）在资源之间进行负载平衡。采用仿真建模的方式，本文将所提出的算法IPSO 与现有的ACO，LBA_HB 和PSO 任务调度算法进行了比较，实验结果表明，改进算法IPSO 能有效地缩短最大完工时间，同时还降低了标准偏差和不平衡程度。除此之外，本文提出的任务调度算法可以通过考虑其他目标函数，如成本消耗等条件，进一步得到扩展和优化。