基于BP 神经网络的火箭弹射击效率计算方法

陈俊霖，侯麒麟，宁文学，王佳丽，王 娟

（北方自动控制技术研究所，太原 030006）

0 引言

毁伤效能评估指在打击目标之前对打击效果的预测，根据武器毁伤能力（威力参数）、目标易损性以及弹药对目标的交会条件（包括精度）进行分析，进而获得武器对目标毁伤效果的预测与评判结论。毁伤效能评估综合了武器威力特征、投射精度、目标易损性等技术领域，其目的是支撑作战规划并优化火力打击参数，实现对目标的高效毁伤。

火箭弹射击效率是指在一定条件下完成射击任务的程度，其表征指标有多种，其中最重要、最常用的指标为毁伤性指标和弹药消耗量指标。毁伤性指标是指在一定射击条件下，发射一定数量的弹药对目标射击所取得的毁伤程度，通常用目标毁伤比的数学期望来表征。射击效率是毁伤效能评估的参考标准之一，在目标打击作战过程中，及时而又准确地完成射击效率的计算，对于毁伤效能评估和现代信息化战争的作战指挥具有重要的意义。目前，火箭弹射击效率是通过数值积分法的近似解求得到，本文给出的基于BP 神经网络的射击效率计算方法对给定的初始计算参数直接计算出射击效率，避免了数值积分法迭代过程中的误差积累，并通过仿真计算验证了算法的有效性。

1 火箭弹射击效率方程及计算方法

本模型主要描述远程制导杀伤爆破弹在给定用弹量条件下对集群中单目标毁伤比的数学期望的计算方法；反之，若给定毁伤程度，计算用弹量的数学期望则可用上述方法迭代计算求得。利用此模型来计算毁伤程度，需要建立在某种假设条件下，因此，首先给出模型假设。

1.1 模型假设

1）根据制导弹制导误差的特点，制导杀伤爆破弹的弹着点误差分布在方向和距离上表现为相互独立的二维正态分布，设其标准差为σ，则σ≈0.849 321 80CEP，其中，CEP 即圆概率偏差。

2）集群目标为连续均匀分布着单个目标的散漫目标，如均匀分布着坦克、火炮、人员等。

1.2 已知条件

1）弹丸效率：杀伤爆破弹对单目标的毁伤幅员v 与平均所需命中弹数ω，取决于弹丸的威力与目标性质。目标性质概略可分为“硬”目标（如坦克等）和“软”目标（如人员、车辆等），弹丸对于“硬”目标需要直接命中才能毁伤，其毁伤率服从指数毁伤率；而对于“软”目标，只需要在弹丸有效杀伤半径内即可毁伤，其毁伤率服从坐标毁伤率，为了便于统一算法，v 取值为：

3）瞄准点：设上述矩形集群目标M 位于XOZ平面的中心（0，0），沿X 方向有m 个瞄准点x（i=1，2，3，…，m）；Z 方向有n 个瞄准点z（j=1，2，3，...，n）。

1.3 毁伤程度计算

1.3.1 一发制导杀伤爆破弹对单目标的毁伤概率

1.3.3 毁伤程度计算

根据假设条件2）和已知条件5），向集群目标M 发射N 发杀伤爆破弹的毁伤程度可表达为：

将上述式（4）、式（5）代入式（6）得：

1.4 弹药消耗量计算

2 BP 神经网络计算射击效率可行性

火箭弹射击效率求解方程为含多重积分的积分方程，通过对求解方程的理论分析及计算验证可知，求解方程的初始计算参数与射击效率之间存在一一对应的关系，若将求解方程视为一非线性系统，则其建立了初始计算参数（输入）与射击效率（输出）之间的一一对应的非线性映射关系。

BP 神经网络是一种多层前馈网络，具有信号正向传递而误差反向传递的特征，由输入层、隐含层和输出层构成，其隐含层层数可按需调整。BP 神经网络最常见的用途是用于非线性映射的拟合，通常3 层网络就已具备不错的拟合能力，能够完成对绝大多数复杂函数映射关系的拟合。除此之外，BP 神经网络还拥有自学习和自适应能力，以及很好的泛化和容错能力。在训练过程中，BP 神经网络可以利用自主学习的能力，找到输入与输出数据间的联系，并把得到的学习结果保存到网络的权值中。而所谓的泛化能力，即训练所得结果不仅适用于样本数据，也适用于非样本数据，学习成果不局限于给出的既定环境中，同样适用于新环境；所谓的容错能力，即在训练过程中，局部神经元出现故障不会对整体训练效果造成很大的影响，能够确保系统的正常运行。

因此，利用BP 神经网络上述的特征和能力，为网络提供足够的训练样本并合理设计网络结构，可建立出满足精度要求的远程制导火箭弹射击效率快速计算的神经网络模型。

3 基于BP 神经网络的射击效率计算

3.1 计算变量的选择

一般来说，BP 神经网络输入变量具有以下特点：输入变量之间的关联性较小和对输出影响较大。在选取输入变量时，可从两方面进行分析，一是从初始计算条件变化对射击效率的影响程度进行分析；二是从求解方程变量之间的内在联系进行分析，两者最终都是要选出对射击效率影响较大的变量。而对于输出变量的选取，通常为要求解的目标值。因此，经过前述方法的分析，并统筹考虑所得结果，最终选择了毁伤幅员的正面与纵深、目标幅员的正面与纵深和毁伤程度作为输入变量，弹药消耗量作为输出变量。

3.2 样本数据和BP 神经网络结构设计

3.2.1 样本数据设计

一般来说，样本数据的设计跟求解方程和变量之间的映射关系的复杂度紧密相关，如何使得选择的样本具有代表性和均衡性是设计的重点。针对本文所研究的内容，采用如下样本设计方案：

1）本文射击效率计算模型，针对的目标主要为暴露步兵、装甲车辆和重型坦克3 类典型目标，三者的毁伤幅员的正面和纵深（单位：m）分别为［60，60］，［50，50］，［20，20］。

2）目标幅员的正面与纵深（单位：m）的区间均为［100，600］，取值间隔为50。

3）由于国内毁伤程度达到55%就表示目标已歼灭，因此毁伤程度的区间为［0.1，0.6］，取值间隔为0.05。

将以上几点进行组合，构成输入样本数据，通过火箭弹射击效率求解方程计算生成输出样本数据，选取部分数据作为测试样本数据，其他为训练样本数据。

一般来说，上述的样本数据在用于训练之前，会先进行归一化处理，通常归一化处理采用下列公式：

式中，x为样本数据的中间值；x为样本数据的最大值；x为样本数据的最小值；x 为样本数据。样本数据在进行上述处理后，最终的结果会落于区间［-1，1］。

3.2.2 BP 神经网络结构设计

在进行BP 神经网络结构设计时，通常输入和输出层能根据已知的计算公式或求解方程获得，因此，设计的关键在于隐含层和隐节点数的确定。

本文主要是实现对样本数据的拟合，根据之前的可行性分析，隐含层设置一层就足够。一般来说，当网络规模较小时，常常通过试凑法来确定隐含层中节点的个数，即在相同训练样本数据下，通过逐渐增加隐节点数，直到获得最小网络计算误差，此时隐含层对应的节点数即为最佳。在进行了大量仿真试验后，得到满足要求的隐节点数为60。因此，BP神经网络结构为3 层，其中输入节点为5，隐节点数为60，输出节点为1，即5-60-1。

3.3 BP 神经网络训练算法及激活函数

目前已经有许多成熟的训练算法，如动态自适应学习速率法、共轭梯度下降法、Levenberg-Marquardt 方法等。根据仿真试验的需要，本文的训练算法采用Levenberg-Marquardt 方法，该方法同时具有牛顿法和梯度下降法的优点，它适用的对象一般具有网络规模较小或样本数据较少的特点，且能获得不错的训练效果。

对于BP 神经网络来说，为隐含层和输出层选取合适的激活函数能在一定程度上提高BP 神经网络的预测精度。常用的3 种激活函数为：线性、S 型和双极S 型函数，一般来说，输出层常选用线性函数，隐含层常选用S 型或双极S 型函数。

除了训练算法和激活函数，BP 神经网络还需设定最大训练次数epoch、训练目标精度goal 和损失函数。根据本文BP 神经网络的网络规模和样本量，经过大量的仿真试验，设定epoch 为800，网络训练目标精度goal 为0，而损失函数一般为均方差MSE，公式如下：

3.4 遗传算法优化BP 神经网络

3.4.1 遗传算法优化BP 神经网络的要素

遗传算法通过优化网络的初始权值和阈值来优化BP 神经网络，从而提高网络预测精度并减小计算误差，优化过程中的基本要素可以概括为以下5 个部分。

1）种群初始化

遗传算法主要的控制参数为种群规模N、交叉概率P和变异概率P，根据BP 神经网络实际的训练需求合理设置，能在一定程度上提升遗传算法的性能；种群个体在综合考虑实际需求的前提下，采用实数编码，每个个体均包含网络中所有权值和阈值。

2）适应度函数

本文将网络的预测和期望输出之间的误差绝对值之和作为个体适应度值F，如下所示：

式中，k 为系数；n 为输出节点个数；o为第i 个节点的预测输出；y为第i 个节点的期望输出。

3）选择操作

进行选择操作的方法有很多，如重组选择、竞争选择、均分选择、比例选择等，本文利用适应度函数求取各种群个体的适应度值，并将适应度值所占比例作为选择标准，则每个个体i 的选择概率p为：

式中，k 为系数；N 为种群规模；F为个体i 的适应度值。

4）交叉操作

根据种群个体的编码方式，采用实数交叉法，第m 个个体a和第n 个个体a在第i 位进行交叉如下所示：

式中，k 为［0，1］间的随机数。

5）变异操作

选取第i 个个体的第j 个基因a进行变异，公式如下：

3.4.2 算法流程

图1 为整个优化过程的算法流程图。

图1 算法流程图

遗传算法优化BP 神经网络大致分为以下3 个阶段：

1）BP 神经网络结构确定

根据火箭弹射击效率求解方程和BP 神经网络的实际训练需求，合理地选择输入/输出参数，进而据此确定网络的结构，得到种群个体的长度。

2）遗传算法优化

通过种群初始化、个体适应度求取、选择、交叉和变异等操作来获得最佳适应度的种群个体，从而实现对BP 神经网络的权值和阈值的优化。

3）BP 神经网络结果预测

根据上述两个阶段，获得最佳种群个体，在训练网络时，用其初始化网络的权值和阈值，从而提高网络预测精度。

4 仿真计算与结果分析

根据本文的样本数据设计方案，最终得到样本数据3 993 组，随机选取3 500 组作为训练样本数据，余下的493 组作为测试样本数据，在此基础上进行BP 神经网络的训练和预测，最后得到仿真计算的结果，见表1。

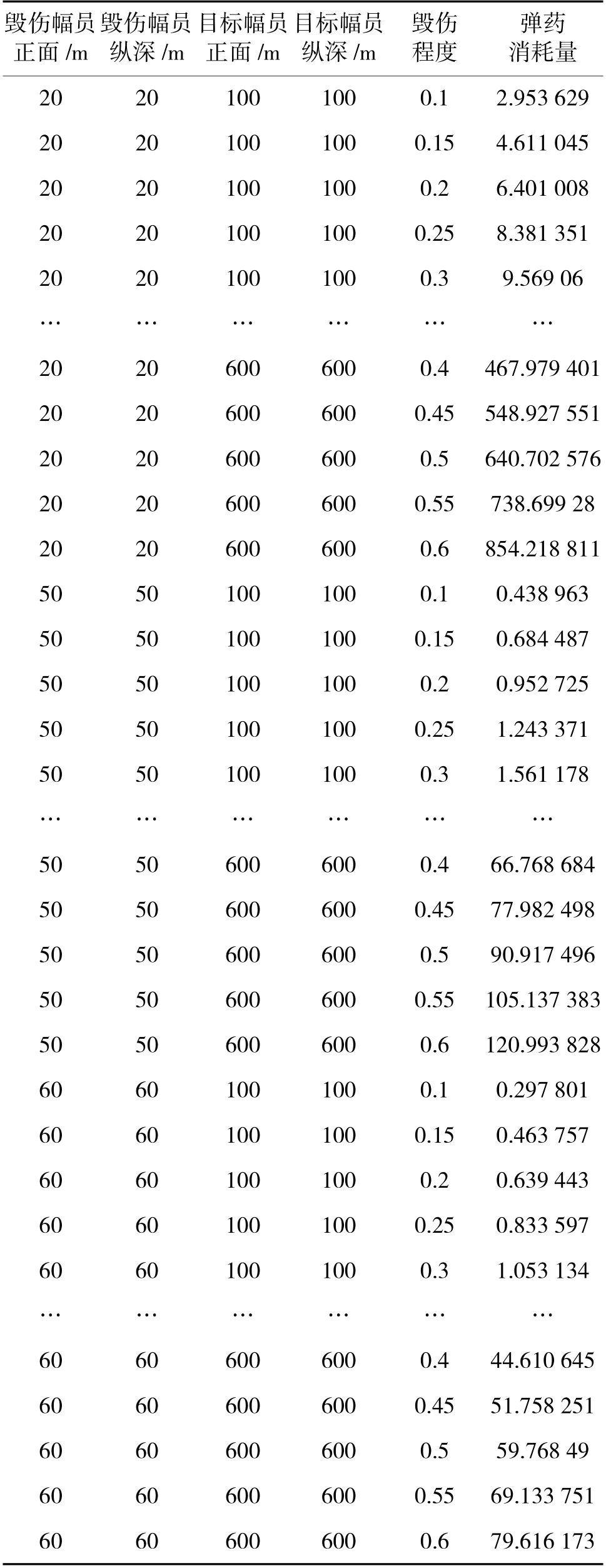
表1 样本数据设计方案所得数据部分展示（部分数据：30 组/总样本数据：3 993 组）

图2～图5 即为仿真计算的结果，其中，图2 为遗传算法优化过程中每代种群个体最佳适应度和进化代数之间的关系图；图3 为BP 神经网络预测测试样本数据时的误差示意图；图4 为BP 神经网络预测测试样本数据时的误差分布直方图；图5 为BP 神经网络训练过程中的性能示意图。

图2 每代种群个体适应度曲线图

图3 BP 神经网络预测测试样本的误差示意图

图4 BP 神经网络预测测试样本的误差分布直方图

图5 BP 神经网络训练的性能示意图

由图2 可知，随着进化代数的增加，每代种群个体的最佳适应度值逐渐降低，直到第50 代之后不再变化，由此获得遗传算法的最佳个体，并用其初始化网络的权值和阈值，从而达到优化BP 神经网络算法并提高网络预测精度的目的。由图3～图5 可知，BP神经网络在经过遗传算法优化之后，对测试样本数据的预测结果的计算误差约有86%落入区间（0，0.001），且计算误差均未超过10数量级。此外，在BP 神经网络的迭代过程中，第201 次迭代均方差达到1.763 5e-06 且此时泛用性最好。因此，本文的BP神经网络正确地找出了所研究方程内部蕴含的规律，并且最终得到的射击效率计算模型的预测和泛化能力也不错，向该模型输入初始计算参数后，可给出满足精度要求的计算结果。

表2 为BP 神经网络对测试样本数据的多次预测结果的误差取平均值后所得统计结果。由仿真计算结果可知：基于BP 神经网络的火箭弹射击效率计算方法的计算误差很小，与利用式（7）计算的结果相比较，计算精度相差不大，能够满足使用要求，且利用模型计算的平均用时不超过5 s。因此，所建立的计算模型有效。

表2 测试样本数据多次预测结果的误差取平均值

5 结论

本文基于BP 神经网络的远程制导火箭弹射击效率计算方法，对给定的初始计算参数可直接计算出射击效率。仿真计算结果表明，该方法计算精度较高，能够满足使用要求，由于火箭弹射击效率的求解过程不进行数值积分迭代计算，因此，极大地提高了射击效率的计算速度。本文算法可为打击目标前快速实现毁伤效能评估与预测提供技术支持。