吊篮流致振动数值模拟及试验验证

王尚武 余志伟 王留兵 李 燕 胡雪飞

（中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213）

吊篮是一类承力部件，所有载荷都是通过吊篮法兰传到反应堆压力容器支承台肩上。反应堆内冷却剂的流动会导致吊篮产生流致振动，长期受到这种振动的影响会造成吊篮结构出现疲劳损伤，进而降低其安全性。研究表明，影响吊篮流致振动的因素有多种，如吊篮自身的结构组成、随机流体激励等。因此常规的理论分析很难全面、直观地确定流致振动响应[1]。近年来，有技术人员尝试运用计算机应用软件构建吊篮模型，并在模型上展开仿真试验，根据试验结果展开分析，从而将获得的流致振动响应数据应用到原型堆。然后在原型结构上设定试验获得的激励荷载，观察原型堆的响应情况。这种方法能够较为简便、准确地获取吊篮的流致振动数值。但是由于试验条件限制，不能完全模拟反应堆实际结构和高温、高温、高辐照的环境，由此得到的分析结果也不会很准确。

针对上述问题，本文按流体-结构耦合分析的方法，针对基于ALE 描述的N-S 方程，采用CBS 算法进行离散，并采用参数化网格法对计算网格进行控制；固体结构采用Lagrange 描述进行有限元分析，构造Newton-Raphson 迭代格式。两者结合，进行流-固耦合分析，以此探索吊篮流致振动数值模拟方法。并以华龙一号反应堆堆内构件吊篮为例，计算它的流致振动响应，其结果对实堆流致振动试验测点的布置进行了指导，实测结果与模拟结果高度一致。

1 数值模拟方法

1.1 Navier-Stokes 方程的ALE 形式

考虑不可压缩的黏性流体，其在ALE 描述下的流体域控制方程的无量纲形式为：

1.2 CBS 算法

CBS 算法主要经过三个过程建立离散的求解方程[3]：

1.2.1 特征线法进行时间差分离散，得到式(2)的时间差分方程：

1.2.3 经典Galerkin 有限元法进行空间离散

采用Galerkin 有限元法离散方程式(4)、(8)和(9)。流场区域采用线性三角形单元，速度和压力采用相同的线性插值基函数Nk进行逼近。

由Galerkin 加权余量法，式(4)可得

1.3 参数化网格划分方法

根据ALE 描述，网格具有自由运动的特性。这一特性虽然客观上降低了大变形问题的计算难度，但是增加了计算量。本文采用参数化网格划分，在此基础上开展有限元分析。在文献[4]中，将有限元法应用到成形模拟中，并基于仿真分析结果验证了有限元法在具体应用中具备的优势和存在的缺陷。同时，该资料中还总结了参数化有限元分析的定义、步骤和技术要点，并且以流程图的方式，简明易懂地展示了参数化有限元分析的流程。

目前可用于构建吊篮有限元模型的工具有多种，比如CAD、UG 以及其它三维建模软件，都具有强大的参数化建模功能。这里以CAD 为例，实际数值模拟过程中，首先在CAD 软件中新建页面，然后导入吊篮的各项参数。对相关参数运用参数化方法处理后可以生成吊篮的三维模型；在CAD 自带的工具库中，挑选相应的网格单元类型，并选择与之对应的网格划分方法。在参数设计选项中输入网格单元的尺寸后，完成对吊篮模型的网格划分，从而得到吊篮的有限元模型。后期如果需要调整模型某个部位的形状、尺寸，只需要调用Updata 函数，就可以在继承当前模型参数的基础上，根据用户需求自动生成另一个新的吊篮模型。这样一来，不仅避免了重复进行网格划分，减轻了工作量，而且还能保证吊篮模型的几何拓扑关系不发生变化，有利于保证模型的精度，为下一步开展模型的仿真模拟提供了必要支持。

1.4 结构有限元分析

结构的有限元分析通常采用Lagrange 描述，其动力学方程为：

将式(15)和式(16)代入式(13)，即可求出t+Δt 时刻的位移、速度和加速度。在非线性的情况下，可构造Newton-Raphson 迭代格式，即：

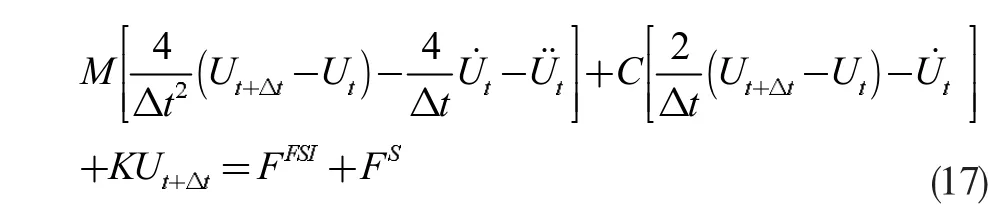
通过以下方法构建“流-固耦合机制”：假设在流体-固体分界面处，某一流体质点的速度与固体质点的速度相同，则固体质点受到来自于流体施加的耦合力。同时，对于此分界面上的流体侧，设定Dirichlet 边界条件；对于此分界面上的固体侧，设定Neumann 边界条件。

1.5 流固耦合迭代算法

在此，流固耦合迭代算法的主要步骤归纳为：

（1）确定某一时间节点（假设为n）的流体变量和结构变量；

（2）在tn和tn+1时刻之间进行FSI 循环；

（3）将所得数据带入方程（17）并计算结果，可以得到tn+1时刻的结构位移、速度和加速度；

（4）按照本文所述的参数化网格法，更新现有的网格；

（5）分别计算流体控制方程(4)，(8)和(9)，可以求出n 时的流体速度和压力；

（6）返回（2）直到时间结束。

2 华龙一号吊篮数值模拟分析

本文利用上述方法对华龙一号吊篮的流致振动问题开展数值模拟分析。为了进一步降低模型分析工作量，本次模拟实验中简化了吊篮结构[5]：用简支代替法兰下的支承筒，用压紧弹簧代替弹簧支承，并且为了保持结构稳定，弹簧支承的直径较大（如图1 所示）。另外，还考虑到热屏蔽板、堆芯支承柱等构件的承压能力较弱，因此数值模拟中只考虑构件自重对吊篮质量的影响。在构建吊篮有限元模型时，可以将热屏蔽板、下堆芯板组建等以等效质量点的形式，添加到吊篮筒体模型上。这样在进行数值模拟试验时，由于模型质心位置保持固定，因此不会影响数值模拟结果的精确性，同时还能简化分析内容，降低分析难度。将二次支承及流量分配结构以等效质量的形式附加到吊篮的堆芯支承板上；吊篮底部通常可以自由移动，这里将其当成自由边界。通过这些简化，建立了吊篮模型。

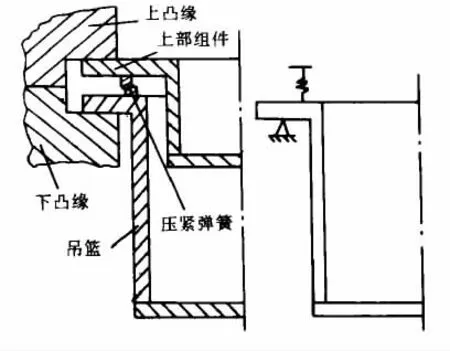
图1 模型边界条件的简化

使用ADINA 软件结合本文方法及简化的吊篮模型，对吊篮在动水中的振动特性进行数值模拟，计算结果见表1，1、2、3 阶振型图见图2、图3、图4。

表1 吊篮流致振动响应计算结果

图2 1 阶梁式振型图

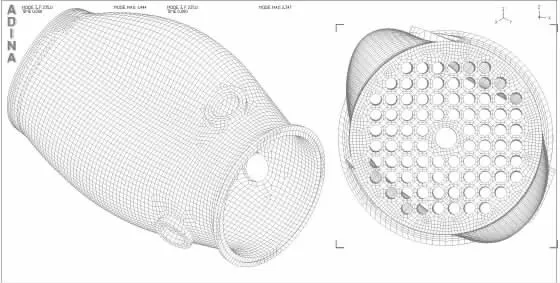
图3 2 阶壳式振型图

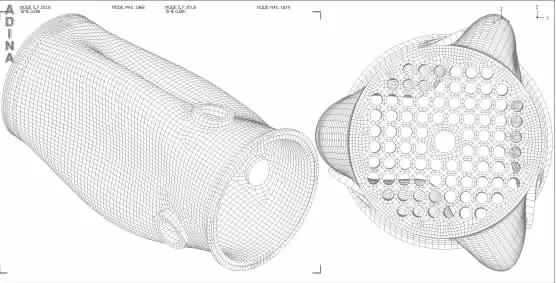
图4 3 阶壳式振型图

3 堆内构件流致振动试验验证

3.1 测点布置

吊篮流致振动数值模拟结果可用于指导实堆堆内构件流致振动试验测点的布置，通常布置在预计振动响应比较大的地方。根据表1 中的数值模拟结果，吊篮法兰根部应变最大。故在福清5 号机组核电厂堆内构件流致振动试验中，在吊篮法兰根部布置了4 个应变计。

3.2 吊篮流致振动试验结果

福清5 号机组核电厂堆内构件流致振动试验吊篮振动响应测量结果见表2。

表2 吊篮流致振动响应试验结果

由表1 和表2 可以看出，吊篮流致振动数值模拟结果和实堆试验结果基本吻合。

4 结论

本文采用基于ALE 描述的CBS 有限元法对堆内构件流致振动问题进行研究，采用参数化网格方法控制网格的运动与更新，建立流-固耦合分析的迭代算法。运用该迭代算法分析堆内构件的流致振动问题，以期得到更加真实、更加精确的流致振动响应。

本文采用该数值模拟方法对华龙一号反应堆堆内构件吊篮的流致振动进行了数值模拟，其结果对实堆的测点布置进行了指导，且福清5 号机组堆内构件流致振动试验结果和数值模拟结果基本吻合，说明本文所述的数值模拟方法具有可行性，可用于其它堆型吊篮或者其它结构的流致振动评价。