有限元分析的准确性验证及应用

欧阳洪 刘新彬 沈雷皓

（湖南工学院，湖南 衡阳 421002）

有限元分析的方法是工程师用来解决问题以及寻找答案的常用方法之一，具体应用涉及到力、冲击、噪音、振动、温度、摩擦、耐久性、刚度和重量等多个方面。用相对简单的问题代替复杂问题，就是有限元分析最基本的理念，替代之后再来求解。有限元法求解的对象是替代后较简单的问题，求解域随之也转换为许多小的子域，数量是有限的，但彼此联系，故称为有限元；然后针对每个单元都给定合理的近似解，再寻求整个域总的解，最后找到问题的最终解。基于有限元分析的基本理念就是问题替代，显然求出的解一定只是近似解，不可能是准确解，但精度还是相当高的。而且实际工程中多数问题确实很难以找到准确解，有限元分析又能够很好适应于各种复杂工况，因此有限元分析成为工程分析中十分常用且有效的一种手段。

有限元分析确实很奇特，用简单的模型就替代了纷繁复杂的现实世界模型，用一个简单软件就能算出理想结果。在有限元分析软件方面，Ansys 软件是通用及专用软件中使用最普遍的软件之一，其在数据共享、与其他建模软件对接（比如CAD）等方面都十分方便，是现代工业设计中工程师特别青睐的CAE 工具。

有限元分析已然发展为计算机辅助分析CAE 的核心。利用CAE 手段可以大大减少或直接避免物理测试过程，其通过计算来模拟出最恶劣工况以及载荷下零件或构件的工况，从而准确地计算出零件或构件产生的应变应力。在产品设计阶段能实现对其数字模型的各种性能指标进行分析评估，对设计上存在的各类问题都能够尽早发现，使产品设计开发周期大大缩短。

尤其是有限元分析及其优化技术，还能改善结构设计的参数使相应产品在满足强度以及刚度等方面性能的前提下，得到更合理的设计方案。不仅如此，在新产品开发包括老产品更新改造方面，基于有限元对应力分布等方面的分析，能够为方案的优化提供很大助力。

1 模型计算

本文设计了对一个对称简支板施加载荷的力学模型，模型具体参数如图1 所示。

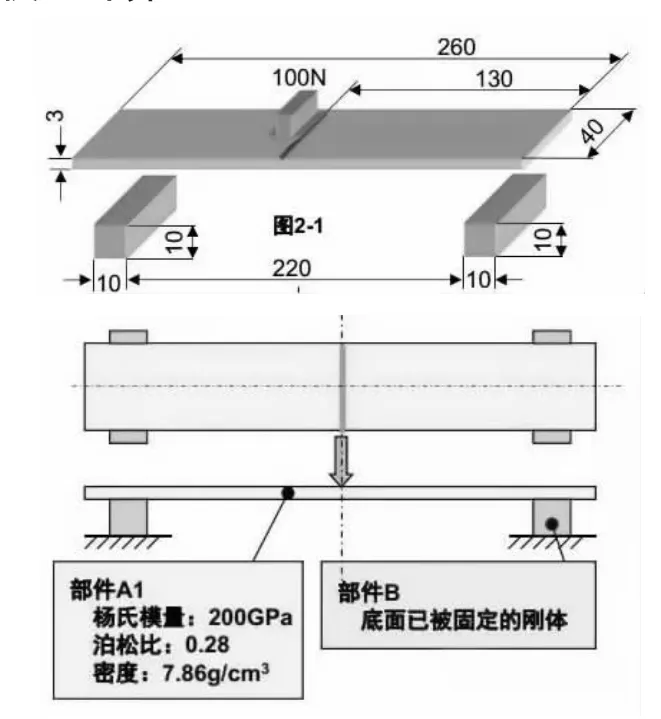
图1

这是一个十分简单而且常见的力学模型，运用材料力学的公式就可以进行相应的理论计算。

计算过程如下：

从结果可以看到，最大应力为91.667MPa，最大位移为1.232mm。

2 有限元分析

Solidworks 属于轻量级、快速的有限元软件。对于普通小模型问题来说，与其他有限元软件结果很近似，尤其是线性弹性问题、非线性弹性问题。

针对普遍的线性及耦合问题的分析求解，运用Ansys 会有不错的结果。当然在工程应用中，非线性问题更为普遍，往往都是将非线性问题进行线性化处理。伴随着科研水平的不断提高和研究不断深入，非线性问题也会成为工程人员、研究人员务必要突破的重大课题，制约设计精确性以及工程进一步深入研究的瓶颈同样也是非线性问题的求解。

鉴于Solidworks 和Ansys 两个软件在线性简单模型分析方面的优势，本文主要就这两种软件进行验证分析。此力学模型是一个十分典型的对称分析求解问题，Ansys 以及Solidwroks 两种软件处理对称模型的策略是类似的。运用有限元分析软件时一定要遵循最基本的分析流程，先对模型简单地进行预处理，由于此简支板模型是完全对称的，故只要将其划分成1/4 模型，再定义好分析类型并且添加材料的属性，密度7.86g/cm3，弹性模量200GPa，泊松比0.28，继续施加载荷以及约束，底部为完全固定的简支梁，即六个自由度都被完全约束，固定不动，模型以及边界条件的施加操作如图2 所示。

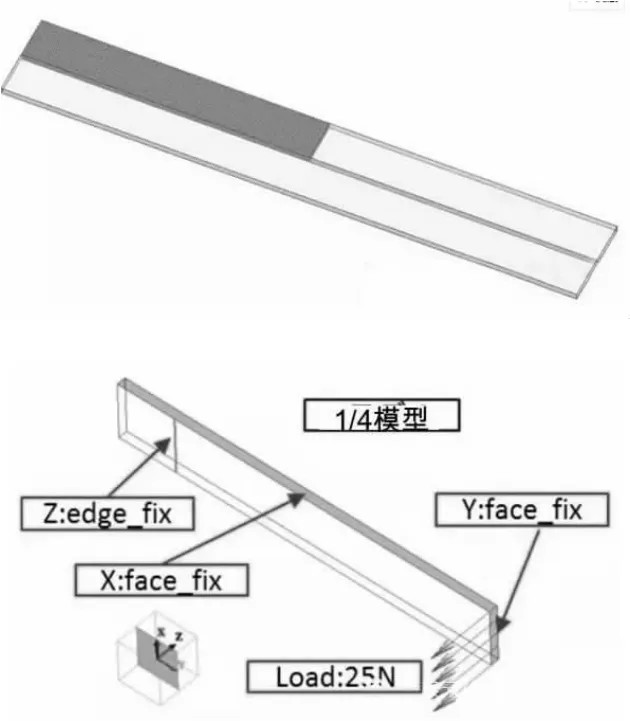
图2

接下来进行划分网格，网格划分常用到几何体是三角形以及四面体，用这些理想的相互联系的几何体去模拟真实几何模型，从而完成有限元网格的划分。并且在对称中心施加130N 的集中载荷，Solidworks 计算的结果如图3 所示。

图3

Solidworks Simulation 求出最大位移的结果为1.239mm，最大应力的结果为92.097MPa。

Ansys 建模分析，为求得精确地结果，本文选用Plane183 单元。具体操作顺序：首先点击“MainMenu”，其次点击“Preprocessor”，随后点击“Element Type”，然后点击“Add/Edit/Delete”，接着点击“Add”，最后点击“Solid”-plane 183。然后进行材料选择，首先点击“Isotropic”，然后将泊松比“PRXY”规定为0.28，弹性模量“EX”规定为2e11。计算的结果如图4 所示。

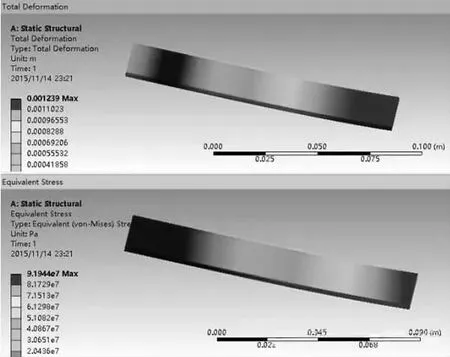
图4

运用Ansys 来进行有限元分析显然是一种更准确的分析手段，此方法能更好了解零件在施加载荷后的形变。简支板的应力云图显示其受力不均匀，中间受力最大。

Ansys 求出最大位移的结果为1.239mm，最大应力为91.944MPa。

综上，Ansys 以及Solidwroks 两个不同分析软件求出的最大位移结果都是1.239mm，与理论计算值1.232 基本一致；与最大应力的理论计算结果91.667MPa 相比，有限元求解值差异也不大。这些结果可以验证有限元分析的准确性还是挺高的，尤其是当有限元软件运用于静力学分析的工况。

3 有限元分析的应用

科技的不断发展和市场需求的不断变化，使得产品设计的周期变得更短，工程领域对新兴技术也有更迫切的需求，而有限元分析方法就是一种能满足需求的技术手段，不仅能是设计周期缩短，而且能使产品质量得到保证，从而提升产品的竞争力。同时，随着计算机领域相关技术的提升和发展，无论科研领域还是工程设计方面，有限元分析在都被应用的越来越广泛，成为了一种能够解决复杂工程问题的有效途径，例如在车辆、航天器的设计和制造方面就十分依赖限元分析。当然，有限元分析在涉及非线性问题以及流体力学等问题时，只有网格划分合理，求解结果才会比较理想。总而言之，一般情况下，好的网格划分是获得比较理想结果的前提基础。

下面以一块大尺寸板的静力分析为案例简述有限元分析的过程：一正方形大尺寸板60m×60m×1m，首先把固定约束施加在板的底端，然后在顶端的节点上施加压力，方向为Y 方向，大小1000N，分析其应力应变情况，具体操作流程如下：

打开Ansys 界面，赋值为结构分析，接着选定新建单元类型，然后把板单元类型定义好，最后把对话框关闭。

新建实例常量，具体操作首先点击“MainMenu”，其次点击“Preprocessor”，接着点击“Real Constants”，然后点击“Add/Edit/Delete”，最后点击“Add”。

接下来就是把单元类型定义好，具体就是选定1 号的shell63 单元，选定后单击“OK”键，此时会弹出新的对话框，在壳厚度栏输入1，单击“OK”键。

定义材料的属性，首先点击“Structural”，接着点击“Linear”，继续点击“Elastic”，最后点击“Isotropic”,把泊松比规定为0.3，弹性模量规定为3e11。

绘制矩形，依次点击“Preprocessor”→点击“Creat”→点击“Rectangle”→点击“By 2 Corners”，原点坐标WP Y=0，WP X=0，Width=60，Heigth=60，最后单击“OK”键确定。

划分网格，依次点击“Preprocessor”→点击“Size Cntrls”→点击“Size”，接着会看到No.of element divisions文本框，输入6，然后单击“OK”键即可。继续点击“Preprocessor”→“Mesh”→“Areas”→“Free”，在对话框单击“Pick All”，将板划分为36 个相等的正方形网格，如下图5 所示。

图5

施加约束及施加负载，首先点击“Solution”，接着点击“Apply”，继续点击“Displacement”，最后点击“On Nodes”，会看到对话框弹出，选择方式设置为Box 即可，接着在板下方捕捉节点，单击“OK”键，然后选择All DOF，在Displacement value 中，直接单击“OK”键即可。最后定义节点集中载荷力，首先点击“Solution”，接着点击点击“Apply”，继续点击“Force/Moment”，最后点击“On Nodes”，同样有对话框弹出，选择方式设置为Box，接着在板下方捕捉节点，单击“OK”键，把节点集中力的方向改为Fy，输入-1000，单击“OK”键确认。如图6 所示。

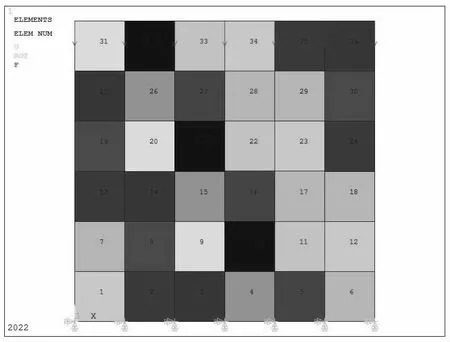
图6

静力分析，依次点击“Solution”→点击“Analysis Options”,在弹出的设置预存应力选项中，直接单击“OK”键，然后点击“Solution”→“Current LS”,单击“OK”键确认，分析结果如图7、8 所示。

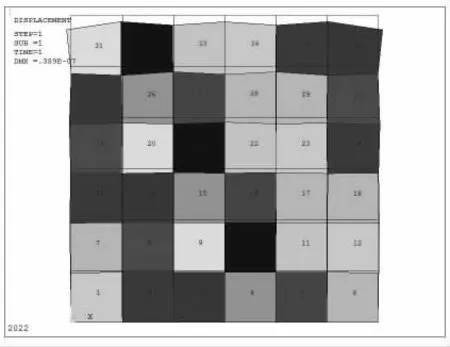
图7

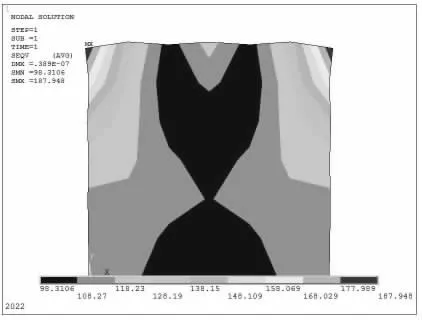
图8

4 结论

有限元分析十分方便快捷，分析结果也很明确，准确性也非常高。基于有限元分析软件可以直接和多种三维软件互通，以及有限元能够处理非线性问题这一优势，有限元分析已经在各行业得到广泛应用，促进了相应的生产力的提高，并且发展趋势是有限元在各行各业的设计中地位越来越高，为我们提高设计效率提供了很好的助力。