基于双重激励含电动汽车的虚拟电厂优化调度

张铁峰，姜喜燕，张灏璠

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

随着全球化石能源紧张及环境污染问题的凸显，推动节能减排受到了国内外的广泛关注。电力行业作为碳排放的主要行业之一，面临着节能减排的巨大压力［1］，因此积极推广使用低碳能源，是电网企业乃至电力系统应对“碳锁定”效应，实现向低碳化转型的重要手段［2］。电动汽车（electric vehicle，EV）因其良好的环保性，近年来发展迅猛［3］。且EV具备电动汽车—电网互动（vehicle to grid，V2G）的潜力［4］，预计2030 年，中国EV 数量将达到6 000 万辆［5］，高峰充电负荷将达479 GW［6］，接入电网时，EV的无序充电会导致“峰上加峰”，给电网运行带来巨大压力。所以将EV与分布式电源整合逐渐成为研究热点［7］。虚拟电厂（virtual power plant，VPP）具备整合分布式电源、电动汽车、储能装置的能力，VPP根据互补电源的特点，通过内部协调，平抑新能源发电的随机性、波动性，使VPP 作为一个特殊的电厂参与电网调度和市场竞争。

目前，在含电动汽车虚拟电厂的优化调度方面已有很多研究。文献［8］针对含有风力发电和EV的VPP参与到电力市场中包含的不确定性问题，提出了一种混合储能虚拟电厂参与电力市场的优化调度策略。文献［9］分析了计及EV、风电机组、光伏机组和需求响应的VPP同时参与双边合同市场、日前市场、实时市场和平衡市场的3阶段竞标模型。文献［10］综合考虑了储能电池、抽水蓄能装置、燃气机组、火电机组的运行特性以及分时电价的影响，提出了VPP双层优化调度模型，但是分时电价激励会引起新的峰谷差。由于电力市场中有多个参与者，因此博弈模型得到广泛地应用。文献［11］构建了VPP 和EV的主从博弈模型，VPP作为EV充电价格的制定者处于领导位置，EV作为响应者处于跟随位置。而碳排放的问题一直是电网研究的重点。文献［12］首次研究包括EV、燃气机组、风电、光伏的VPP参与碳交易的情形，建立了经济与环境调度模型。文献［13］建立了考虑碳排放需求响应的VPP 优化调度模型，研究了节能减排对VPP经济效益的影响。

综上，目前关于VPP 削峰填谷的研究大多集中在经济效益或碳排放问题，忽视了VPP 在优化调度过程中可能出现新的峰谷差问题，对此本文在考虑VPP、EV车主效益及碳排放的基础上，将VPP出现的新峰谷差问题考虑在内。利用主从博弈思想，提出基于分时电价和碳配额双重激励的含电动汽车的虚拟电厂优化调度模型。针对VPP内的等效负荷曲线设置峰平谷时段，并根据此时段制定分时电价和碳配额双重激励政策，引导EV 有序充放电。建立以VPP侧为主体，EV侧为从体的博弈模型，在保证VPP经济效益的同时，使EV的充电成本最小，同时避免新的峰谷差出现。

1 含EV的VPP调度分析

1.1 含EV的VPP调度模式的分析

对于包括新能源发电、化石型能源发电、EV 及负荷的VPP，其优化目标为在满足用户负荷需求的前提下，通过制定合理的峰平谷电价和碳配额激励政策，充分挖掘EV 的双向调节能力。调度架构如图1所示。

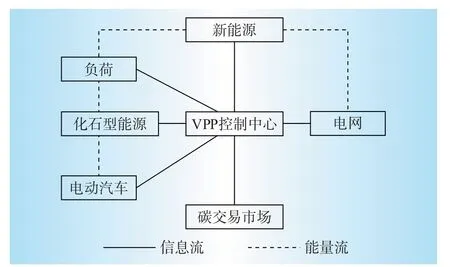
图1 VPP调度架构Fig.1 Dispatching framework of VPP

VPP根据负荷信息和新能源出力信息制定合理的分时电价和碳配额激励政策，引导EV 有序充放电，减少弃风弃光现象，平衡VPP内的峰谷差，未平衡部分由化石型能源和电网的购售电调节。此外，VPP 和EV 都可以在碳交易市场中购买或售出碳排放权来获得收益。

1.2 EV的行驶特性分析

有研究表明，燃油汽车每天大约有95%的时间处于空闲状态，假设EV 和燃油汽车的停驶概率一致，根据文献［14］中的停驶概率得到如图2 所示的EV的停驶概率分布图。

图2 EV停驶概率Fig.2 Stopping probability of EV

2 基于双重激励的含EV的VPP优化调度

2.1 双重激励政策

VPP 中负荷和新能源出力都具有随机性的特点，且两者的峰谷差不同步，VPP调度的压力主要来源于源荷平衡后的等效负荷曲线，所以引入等效负荷的概念［15］，表示为

本文假设VPP 内的化石型能源只有燃气机组，对含EV的VPP，EV的充放电行为具有随机性，若EV无序充放电，会造成“峰上加峰”，因此需制定合理的激励政策，引导EV充放电行为有序化，用EV分担燃气机组的压力，即当等效负荷不为0时，优先通过EV实现平衡，然后使用燃气机组实现平衡，最后通过向电网购售电实现平衡，此时的等效负荷表示为

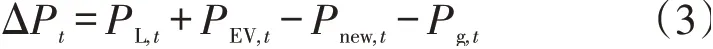
式中：Pg,t为燃气机组的出力值；PEV,t为所有参与调度EV的充放电功率，PEV,t ＞0 表示EV充电，PEV,t ＜0表示EV 放电，PEV,t的值取决于VPP 控制中心给予的激励政策，PEV,t反过来也影响着激励政策的制定。

VPP控制中心根据等效负荷ΔPt制定分时电价和碳配额的激励。

（2） ΔPt ＞σ，新能源出力不足，实施高电价，并将碳配额奖励给放电的EV，充电EV 无奖励。引导EV 放电补充新能源出力的不足，减少燃气机组出力，降低成本，直到| |

ΔPt≤σ无碳配额奖励。（3） ΔPt ＜-σ，新能源出力过剩，实施谷电价，并将碳配额奖励给充电的EV，放电EV 无奖励。引导EV 充电来消纳多余的新能源出力，减少弃风弃光的现象，提高新能源就地消纳能力，直到| |

ΔPt≤σ

无碳配额奖励。

2.2 碳配额机制

为实现减少碳排放的目标，各国目前都在积极开展碳排放权交易，这是利用市场手段实现温室气体减排的措施之一，政府在总量控制的前提下，将排放权以配额方式发放给各企业［16］。在国内，对发电企业一般采用2 种分配方法，即历史法和基准线法，因历史法所需数据较多，主流方法是基准线法，本文也采用基准线法。对于含风电和燃气机组的VPP，在时段t分配到的碳配额为

3 含EV的VPP优化调度模型

对于含EV 的VPP，EV 和VPP 分属于不同的利益主体，都追求各自利益最大化。本文针对等效负荷，提出基于分时电价和碳配额双重激励协同博弈的含EV 的VPP 优化调度模型，该模型中VPP 作为激励政策的制定者处于主体位置，以VPP 的收益最大化为优化目标，EV作为激励的响应者处于从体位置，以EV侧成本最小为优化目标。针对VPP侧，通过调整分时电价并把一部分碳配额奖励给EV 车主，可以减轻燃气机组的压力，降低自身成本；对EV侧，可以通过调整自己充放电的时间，获得一定差额补贴和碳配额奖励。

3.1 目标函数

（1）VPP侧目标函数

VPP 作为主体位置，首先确定峰平谷时段及各时段的电价和碳配额奖励，引导EV 有序充放电。VPP侧的目标函数为收益最大化，表示为

（2）EV侧目标函数

EV作为响应者处于从体位置，基于VPP控制中心制定的分时电价和碳配额激励政策，EV车主充分利用峰谷差价和碳配额奖励调整自己的充放电时间，降低自身成本，其目标函数为成本最小化，表示为

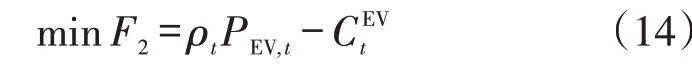
3.2 约束条件

（1）分时电价约束

分时电价的设计应以VPP 的总售电收益不变为基本原则［17］，需满足以下条件：

式中：Cmax为燃气机组爬坡率的最大值。

3.3 优化模型求解

论文采用Matlab+Yalmip+Cplex 求解优化模型，具体的求解过程如图3所示。输入基本的参数及初始分时电价，VPP处于主体位置，以VPP的收益最大化为优化目标，EV处于从体位置，以EV侧成本最小为优化目标建立主从博弈模型，依据初始分时电价及约束条件，由minF2求得EV 的充放电策略。依据充放电策略并结合minF1求得最优分时电价γ，根据分时电价γ和minF2求得最优的充放电策略χ，以此循环迭代，且迭代结果与相邻结果的目标函数值小于一个很小的正数σ后结束迭代，即找到纳什均衡解{γ,χ} 。

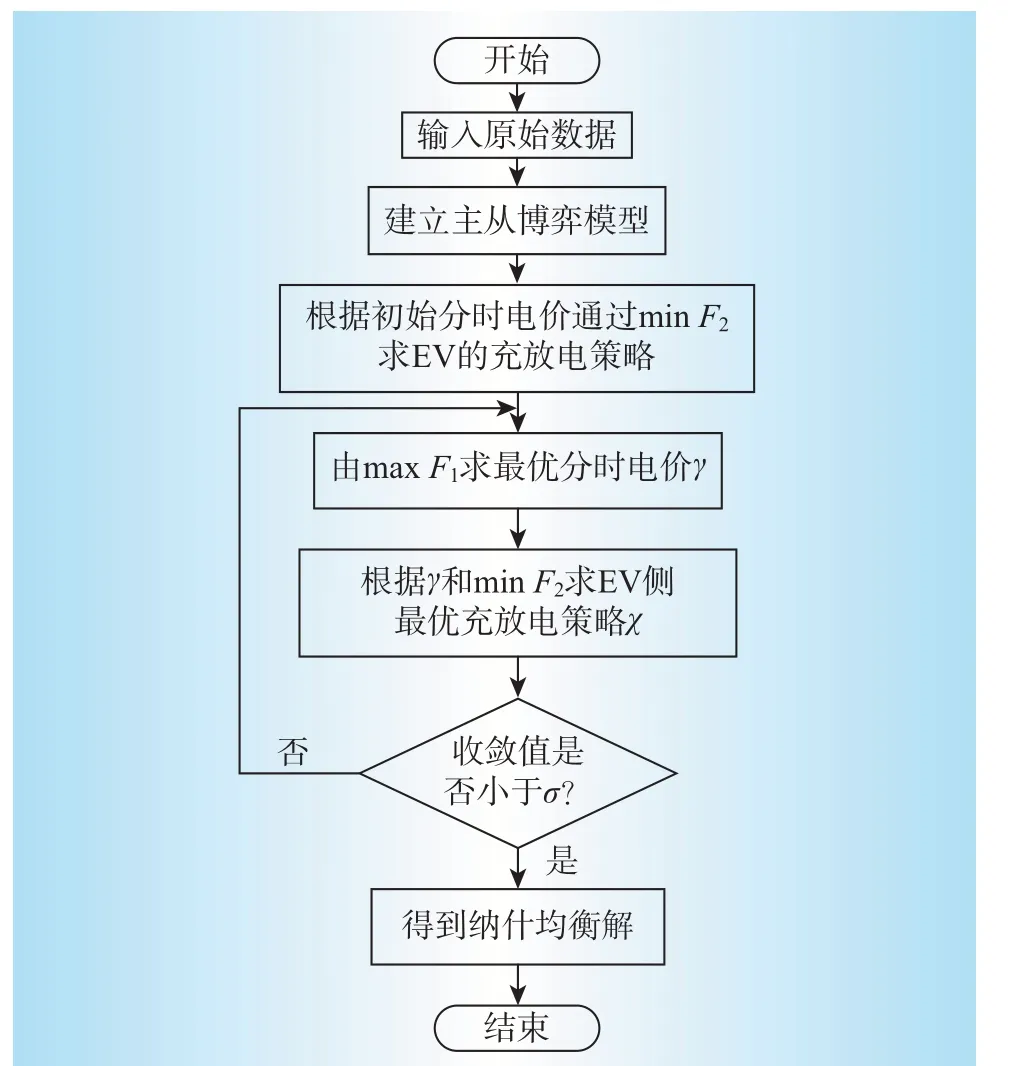
图3 模型求解流程Fig.3 Model solving flow

4 算例分析

4.1 参数设置

以由3台燃气机组、1个风电机组、250辆EV 及负荷组成的VPP 为例，来验证本文方法的有效性和优越性。碳交易价格为0.25元/kg，燃气机组碳排放强度为0.81 kg/kWh，VPP 单位电量碳排放分配系数为0.728 kg/kWh，风电机组出力及负荷需求参考文献［15］，燃气机组运行成本系数［11］a=0.007 1 ，b=0.233 3，c=0.433 3，爬坡率为25 kW/h，启停成本均为180元。电网实时购售电价格参考文献［18］，EV 的具体参数参考文献［15］，正数σ为0.001。初始分时电价如表1所示。

表1 初始分时电价Table 1 Initial value of time-of-use price元/kWh

4.2 优化调度结果及分析

根据风电机组出力及负荷需求，得到图4 所示的优化前的等效负荷曲线。

图4 EV入网前的等效负荷曲线Fig.4 Equivalent load curves before EV enters the network

由图4看出，风电出力和负荷的峰谷差不同步，加入风电后，等效负荷出现了新的峰谷差时段和峰谷差值。VPP需要在保证自身收益的同时，给予EV车主合理的分时电价和碳配额双重激励政策引导EV 充放电来平衡等效负荷峰谷差，消纳新能源出力，减少燃气机组的出力。表2 是考虑双重激励政策下的峰谷差时段及优化前后的分时电价。

表2 考虑双重激励的优化前后分时电价Table 2 Time-of-use price before and after optimization considering dual incentives元/kWh

表2中，ρ0和ρt分别表示优化前后的分时电价。可以看出，优化后峰时电价上升的同时谷时电价下降，平时电价基本不变。结合图5可看出，EV基本都在谷时充电，峰时放电，体现了本文所提模型的有效性。

图5 双重激励下的EV充放电策略Fig.5 EV charging and discharging power strategy considering dual incentives

为验证双重激励政策能有效避免新的峰谷差出现，本文将仅考虑分时电价激励和双重激励下的等效负荷曲线进行对比，如图6和图7所示。

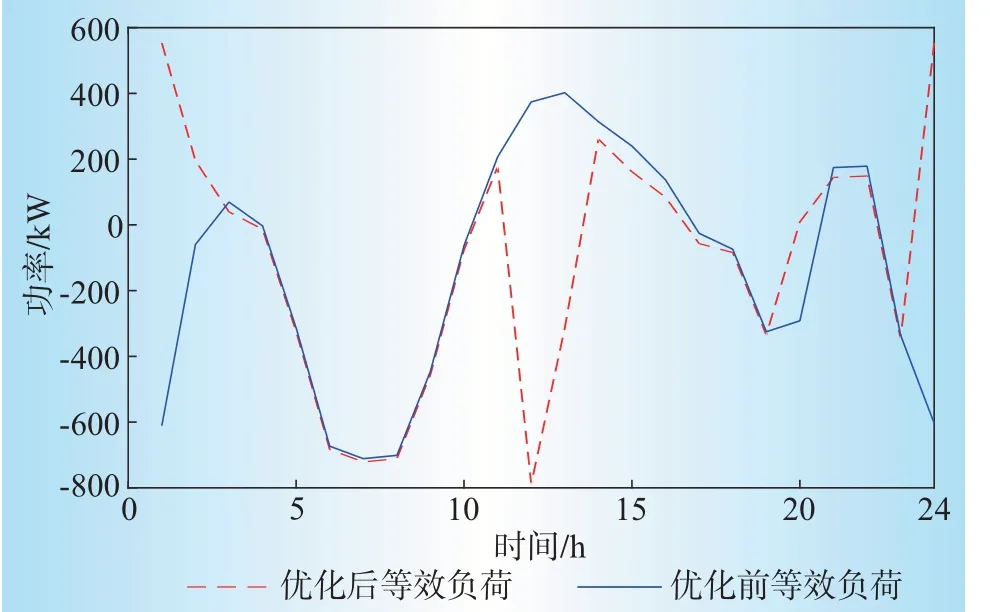
图6 分时电价激励下的等效负荷曲线Fig.6 Equivalent load curves under the incentive of time-of-use price

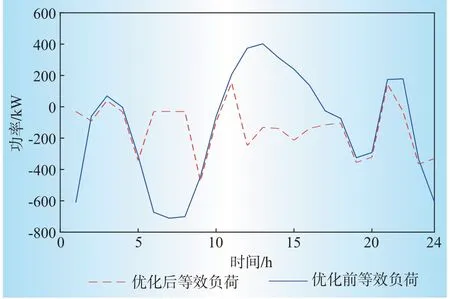
图7 双重激励下的等效负荷曲线Fig.7 Equivalent load curves under dual incentives

图6仅考虑分时电价激励政策，EV在23:00—次日3:00 电价低时大量充电，且在12:00—14:00 电价高时大量放电，引起了新的峰谷差，给VPP 的稳定性造成严重影响。实际上，只要有峰谷差价，EV 车主就会选择在峰时集中放电，谷时集中充电，不可避免会导致新的峰谷差出现。

从图7考虑双重激励政策下的等效负荷曲线看出，EV在峰时放电，谷时充电，且由于碳配额激励的协同作用，在等效负荷趋于0时，EV车主停止不必要的充放电行为，从而避免了新的峰谷差出现，达到了很好地削峰填谷的效果。结合图5 可以看出，在6:00—8:00及12:00—13:00，等效负荷较大时，更多的EV参与调度。最终的等效负荷曲线通常位于0值之下，说明双重激励政策在减小VPP压力的同时，还可以将多余的电量出售到电网公司获得更多的收益。表3给出了2种模型下VPP侧和EV侧的收益对比。

表3 VPP侧和EV侧的收益对比Table 3 Comparison of revenues on the VPP and EV元

由表3可以看出，由于碳配额的协同作用，减少了燃气机组的出力，降低了VPP 侧的成本，同时将碳配额转换为VPP 侧和EV 侧的收益，双重激励模型下VPP 侧和EV侧的收益都比仅考虑分时电价模型时多。其中，VPP 侧总收益增长了46%，EV 侧收益增长了91%。

论文分别分析了含150、200、250、300 辆EV 参与调度时的等效负荷，比较曲线如图8 所示。将等效负荷功率值标准化处理，表4 给出了标准化后等效负荷的峰谷差率。综合图8 和表4 可知，本论文EV数量为200辆时，削峰填谷效果最好。

图8 不同数量EV的等效负荷曲线Fig.8 Equivalent load curves of different numbers of Evs

表4 不同数量EV等效负荷峰谷差率Table 4 Peak-to-valley difference rate of equivalent load of different numbers of EVs

5 结论

本文针对含EV 的VPP 在分时电价激励下会出现新的峰谷差的问题，提出基于双重激励协同博弈的含EV虚拟电厂的优化调度模型。以VPP 侧为主体，EV 侧为从体建立主从博弈模型，最终求得最优分时电价和充放电策略的博弈均衡解，本文所提模型具有以下优势：

（1）相比于分时电价的单一激励，在增加碳配额激励的双重激励政策下，可以减少燃气机组的出力，既减少了碳排放，又降低了VPP 的成本。将碳配额转换为VPP 侧和EV 侧的收益，两者的收益比仅考虑分时电价模型时明显提高。

（2）由于碳配额的协同激励作用，可以避免新的负荷峰谷差出现，提高VPP 的稳定作用能力，本文所提模型可以为EV入网有序充放电相关实践提供依据。

（3）在本文所提模型下，负荷峰时电价上升，谷时电价下降，适当拉大了峰谷电价差，有助于激励到位，但实施需要相关政策的支持。D