回归运算性质,统领基本题型下的不同情境
2022-07-22江苏东海县黄川中心小学222300朱惠敏
江苏东海县黄川中心小学(222300)朱惠敏
自从原本自成一派的应用题单元正式退出历史舞台,只是作为一种题型分散于各个学段后,教师就需要调整教学思路,摸索新的教学方式。为此,笔者对一、二年级的学生进行应用能力的测试,发现了一些不容忽视的问题。
一、两次测试带来的思考
在对一、二年级的问卷调查中,笔者编录了一些一级运算的一步计算应用题。首次测试安排在一年级下学期教学“认识10以内的数”以后,第二次测试安排在二年级开学前半月。调研的目的是考查一年级下学期的学习对学生的实质帮助有多大。
【测评试题】商场的升降电梯从1楼上升到9楼,共升高了几层楼?
【数据解读】
分析表1可知,一年级学生对这类情境逼真的问题有超强的悟性:有61%的学生可以吃准题意,但由于自身知识所限,仅有8%的学生正确算出“9-1=8”的答案;10%的学生凭直觉推出答案是8,但是不会列式;43%的学生既推理出答案是8,也会按照自己的意愿列式,但遗憾的是表达出错。经过一年级下学期的磨砺,二年级的学生数学表达能力明显增强——完全正确的学生占比从8%提至70%,但仍然有16%的学生存在解题障碍,错误集中在“1+9=10”。
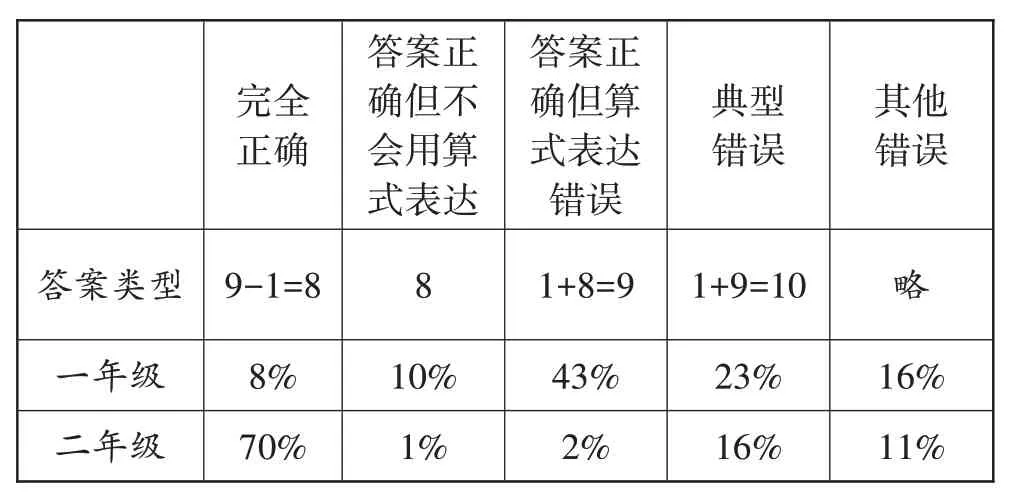
表1 测试情况汇总表
之所以选择在一、二年级做这样的问卷调查,是出于多种原因的考量。第一,一年级末到二年级初,学生仍旧处于形象思维的成长期,学生在处理一些一步计算题时,一般都是按照直观思维来推导的。也就是说,学生在一年级学习的最简单的加减法都是利用物品的合并和分堆这些直观表象的,如“从9个苹果里拿走1个苹果,还剩几个苹果?”“果篮里本来只有1个苹果,又放进8个苹果,现在果篮里共有几个苹果?”。到了二年级,这些直观表象仍然存在,学生依然需要它们,但是为了顺应学生的思维发展,教材对这些直观表象进行了一定程度的抽象化处理,那就是把过去的实物(苹果、梨子、小鸟、金鱼)抽象成楼梯、年龄、体重等,如“明明1岁,哥哥9岁,哥哥比明明大几岁?”“明明体重50千克,爸爸体重80千克,爸爸比明明重多少千克?爸爸和明明一共重多少千克?”等,这些数量虽然有具体表象支撑,但是变得较为抽象,学生可能不知道50千克究竟有多重,9岁(二年级学生才七八岁)有多大,但是借助一年级积累的运算经验,他们也能正确列式。因此,题目“电梯从1楼上升到9楼,共升高了几层楼?”正好处于“半抽象半形象”的状态,可以从算式的列法上考查学生对应用题解法的掌握情况。
二、访谈及成因分析
分析数据时,有两个数据很“扎眼”:一是一年级学生中自主列式“1+8=9”的比率达到43%;二是二年级学生中列式“1+9=10”的比率从原先的23%减至16%,仅回跌7个百分点。前者是起步,也是教师的施教重点;后者是学习成效,也是需要克服的困难。鉴于此,笔者对上述两类学生展开访谈。
直面学生学习的起跑线,先对列式为“1+8=9”的学生进行访谈,学生反馈的信息是:“从1楼到9楼,还差8层楼,1加8才等于9。”学生的答复表明,他们能明确“1楼+上升的8楼=9楼”这一基本的数量关系,但由于没有受过正规的列式训练,因此他们习惯于按照事情发展线索顺向列式。事实上,本题应按倒推方式逆向列式,也就是采用“结果数-运算数=起始数”的逻辑方向列式,但这种表述需要调换次序和句式,还要根据事理逻辑对句式进行倒装,因此对于未受过专业训练的学生来说难度不小,而这恰恰是一年级下学期的教学重点。
一年级学生列出“1+8=9”这个算式实属正常,因为受到形象思维的影响,学生做加法只会想到两堆物品的合并,做减法只会想到从一堆物品中拿走一些。因此,“电梯从1楼上升到9楼”这个“半抽象半具体”情境已经超出学生的认知范围(到二年级才会学习抽象的运算模型),此时学生就会自动在脑海里将其还原成原有模型——如替换成“1个苹果加多少个苹果变成9个苹果”的类似情境,因为它们无论是从表述上还是从实际意义上都是按照两个量合并的思维来传递信息的,学生自然会按照加法的固定思路来列式,这在一年级的训练中不乏其例,如“1+□=9”。这是按照逆运算的思路来做减法,也就是“想加做减”,表面上做加法,实际上做的是减法。
为什么会出现这种情况呢?根本原因还是由于运算的抽象化还未起步(到二年级起步),学生的形象思维过于模式化,“苹果情境”尚可通过改进转化成标准的减法模型——“左边有9个苹果,右边有1个苹果,左边比右边多几个苹果?”或者“原有9个苹果,拿走1个,还剩几个?”,但是“楼梯情境”则难以改进,“从9楼里拿走1楼,还剩几楼?”“这边9楼,那边1楼,这边比那边多几楼?”都说不通,只有勉强改成“9楼比1楼高几层?”,而这种改进需要抽象思维发展到一定程度才能完成,因为“楼层”毕竟不像“苹果”那样可以随意移动。
经过一个学期的历练之后,列式为“1+9=10”的学生的比率从原先的23%变为16%,改观并不大,原因是什么?笔者对列式为“1+9=10”的学生进行访谈,学生主要存在两种观点:第一种就是揪住“升”字不放,望文生义,想当然觉得“升高”就用加法;第二种就是纠结于一个“共”字,曲解其意,过度解读,自作聪明地盲目相加。对一、二年级学生进行访谈得出的结论基本一致。这样列式的学生都陷入了断章取义地推测题意的误区,出错在所难免。
研究发现,学生抓住个别词眼来对整个题意妄加揣测的毛病与以往歪打正着的“成功”经验有关,比如,对于“有15瓶蜂蜜,喝了9瓶,还有几瓶?”等类似问题,直接将“喝”字与“减去”画等号。之后学生遇到类似的物品外流的词语,如“分给”“运走”,也会直接将其和减法等同起来。当这样的思考方式一次次奏效后,学生就会对这种词汇替换法更加信赖,逐渐形成思维定式。
对一年级下学期所有习题进行整理,发现涉及减法的习题总共32道,几乎每道题都包含“剪掉”“拿走”“售出”“吃掉”“……比……多……”“……比……少……”等带有暗示性的词语。加法习题共5道,都含有“再加”“一共”等算法暗示性措辞,而每道习题的算法恰好与提示词吻合,这就使一些学生更加认定,用关键词判断题意轻松便捷,是一种窍门。另外,学生如果只认关键词,一旦关键词在句型中的位置发生变动,解题方式也会受影响。一、二年级的学生读取关键词的注意顺序不同,一年级学生习惯优先提取暗示加减法含义的关键词,如“升到9楼”,然后按照既定算法填数。相对来说,二年级的学生能整体理解题目大意,全面考虑问题,更加注重问题中的导向性提示词,并据此来构思解题策略,如问题中的“共升高了几层楼”。
三、教学启示与思考
通过测试、访谈和分析,学生在一年级下学期的学习起点和难点一一显形。
从一年级学生的实际出发,以及考虑到学生的认知规律,在问题解决初期,适当使用提示词解读法,的确有助于学生迅速掌握基本解题思路。但如何做才能既厘清数量关系,又不束缚学生思维?那就要返璞归真,从两数关系组成的表象出发,进行专项训练。应用题是分散在各阶段的计算教学中的,计算教学大多又是以数字的拆组为理论基础。那么对于应用题的解题方法教学,教师可以“算用”结合,引导学生回到数字的拆组中寻求解题之道。
如“货柜上有13盒伊利优酸乳,取下6盒伊利优酸乳,还剩几盒?”,在审题时,教师只要让学生边读题,边试着将题中的数据进行拆组演示即可(如图1)。
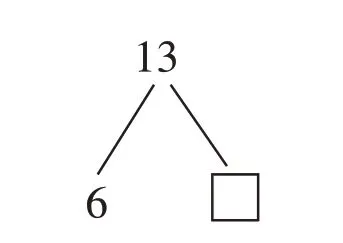
图1
学生原有的数的拆组经验被激发并自动迁移,学生很快就明白,求“还剩几盒”,就是求总数13中余下的部分,用减法算。如此,同样是对题目的字面意思进行解读和推导,但学生的注意力已经离开表示加减法的提示词,回归到数量关系的整体把握和理性判断上,更多地关注总量与部分、整体与局部的关系,从而杜绝了只认关键词的弊病。
一步加减应用题解决的是浅易的数量关系,如何选择运算方法是解题重点。一年级下学期,学生初步具备分析能力,能从不同角度全面考虑问题。如图2所示的题目,学生一般会从两个角度剖析。
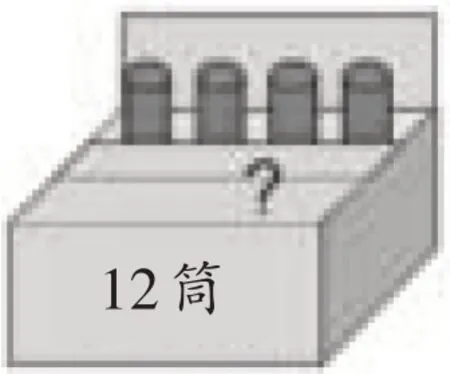
图2
一种是“食品包装箱里已有4筒乐事薯片,再装几筒后能装满一整箱(规格:12筒装)?”,是全面看待问题、服从大局的整体思维,4+□=12(筒);另一种是“食品包装箱里能装12筒乐事薯片,已经装了4筒,还能装几筒?”,是以残缺条件为最终问题的局部思维,12-4=□(筒)。对于学生而言,思路不同,选择的解题方法就随之不同。这样的典型题,如果教师在读题时就指引学生进行数字拆解(如图3),借助数的组成关系图,学生就会重新思考题中的数量关系,清醒意识到:两种思路是辩证统一的,都是处理一个整体与两个部分的关系。这样加减换位思考,以及整体与部分的数量关系转换,有助于学生透视应用题的逻辑结构,对各种数量关系以及条件与问题的因果关联洞若观火。如此一来,经过各种不同情境、结构的同类题的训导,学生脑中就会形成问题的数字架构,而不是盯住个别词眼不放。
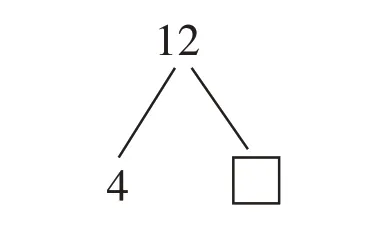
图3
对于一年级下学期的一道题“蛋糕店有一批蛋挞,又进货36箱,现有78箱,蛋糕店原来有多少箱蛋挞?”,解题思路是“蛋糕店原有的蛋挞+进货的36箱=现有的78箱”,但列式却是用减法“78-36=42(箱)”。这类题目迷惑性较强,但在教材里仅有3例。因此,讲解时,教师应该对学生进行题组训练,提高学生以问题为导向,重组数量关系、自定义算法的能力。建议编设以下题组:
①蛋糕店有一批蛋挞,又购进36箱,现有78箱,蛋糕店原有多少箱蛋挞?
②蛋糕店有42箱蛋挞,新购一批后,现有78箱,新购的蛋挞有多少箱?
③蛋糕店原有42箱蛋挞,新购36箱,蛋糕店现有多少箱蛋挞?
通过变换句式,实现问题与条件叙述的调换,可以得到一组习题。在解答题组的过程中,教师照旧可以使用数字拆组法来教学(如图4)。
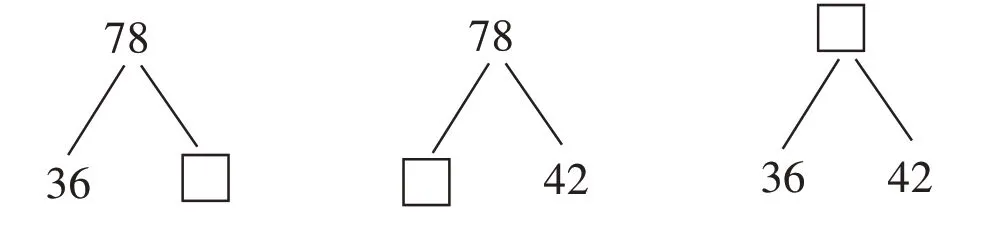
图4
这样,将情境一致、结构基本相同的一组习题变成题组,学生通过比较辨析就能从不同角度掌握整体与局部的稳定数量关系,形成理性的、全面的认识。
