Weighted composition operators on Bers-type spaces of the first kind Cartan-Hartogs domains

-

(College of Mathematics and Statistics, Zigong 643000, China)

Abstract: Let YI(N,m,n;K)be the first kind Cartan-Hartogs domain, φ a holomorphic self-map of YI(N,m,n;K)and u∈H(YI(N,m,n;K))the set of all holomorphic functions on YI(N,m,n;K).In this paper, by using the generalized Hua’s matrix inequality, the boundedness and compactness of the weighted composition operators Wφ,u:f→uf∘φ on Bers-type space of the first kind Cartan-Hartogs domain are characterized.

Keywords: Weighted composition operator; Generalized Hua’s matrix inequality; First kind Cartan-Hartogs domain; Bers-type space; Boundedness; Compactness(2010 MSC 32A37，47B33)

1 Introduction

The Bergman kernel function plays an important role in several complex variables.But, for which domains can the Bergman kernel function be computed by explicit formulas? In general, it is difficult to get the domain whose Bergman kernel function can be gotten explicitly.It is well known that all irreducible bounded symmetric domains were divided into six types by Cartan in 1930s.The first four types of irreducible domains are called the classical bounded symmetric domains as well as the rest two types are called exceptional domains consisting of two domains(16 and 27 dimensional domain, respectively).In 1998, Yin and Roos introduced four kinds of domains corresponding with the classical bounded symmetric domains and called this four kinds of domains as Cartan-Hartogs domains[1-27].Yin has obtained the explicit Bergman kernel functions for the first Cartan-Hartogs domain in Ref.[26].

In this paper, we study the firstkind Cartan-Hartogs domain denoted byYI(N,m,n;K), which is expressed by the following form:

YI(N,m,n;K)={W∈CN,Z∈RI(m,n):

whereK>0 and RI(m,n)denotes

Let Ω be a domain ofCnandH(Ω)the class of all holomorphic functions onN.Letφbe a holomorphic self-map of Ω andu∈H(Ω).The weighted composition operatorWφ, uon some subspaces ofH(Ω)is defined by

Wφ,uf(z)=u(z)f(φ(z)),z∈Ω.

Ifu=1, it becomes the composition operator, usually denoted byCφ.Ifφ(z)=z, it becomes the multiplication operator, usually denoted by Mu.A standard problem is to provide function theoretic characterizations whenφanduinduce a bounded or compact weighted composition operator.In recent years, there is a great interest in the weighted composition operators on or between spaces of the various bounded domains(see,e.g., Refs.[3, 5, 12, 15, 16, 19]for the unit disk, Refs.[11, 17, 18, 20]for the unit ball, Refs.[13, 23, 24]for the unit poly disk, Refs.[1, 2]for the bounded homogeneous domain and Refs.[8, 10, 21, 22]for the half-plane).

Letα>0 and={z∈Cn:|z|<1} be the open unit ball ofCn.The well-known Bers-type space on, usually denoted byAα(), consists of allf∈()such that

For the Bers-type spaces and some concrete operators on them, see,for instance, Refs.[6, 7, 9, 27]and the references therein.

Letα>0,K>0.Following the definition of Bers-type space on, we say thatf∈H(YI)is in the Bers-type spaceAα(YI)if

|W|2K]α|f(Z,W)|<+∞.

It is not difficult to see thatAα(YI)is a Banach space under the quantity ‖·‖Aα(YI).

Motivated by the results of weighted composition operators on holomorphic function spaces of the classical domains, we study this kinds of operators on Bers-type space of the first Cartan-Hartogs domain and characterize the boundedness and compactness.

Throughout this paper, the constants are denoted byC, which is positive and may differ from one occurrence to the next.

2 Preliminaries

First, we have the following easy result.

Lemma2.1Letα>0,K>0.For each(Z,W)∈YIandf∈Aα(YI), it follows that

In order to characterize the compactness, we need the following result which is similar to Proposition 3.11 in Ref.[4].

Lemma2.2Letα>0,K>0,φbe a holomorphic self-map ofYIandu∈H(YI).Then the bounded operatorWφ, uis compact onAα(YI)if and only if for every bounded sequence {fk} inAα(YI)such thatfk→0 uniformly on every compact subset ofYIask→∞, it follows that

(1)

ProofAssume that the bounded operatorWφ,uonAα(YI)is compact.Let {fk} be abounded sequence inAα(YI)such thatfk→0 uniformly on every compact subset ofAα(YI)ask→∞.If ‖Wφ,ufk‖Aα(YI)→0 ask→∞, then there exists a subsequence {fkj} of {fk} such that

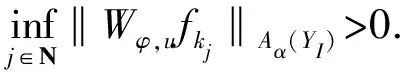
SinceWφ, uis compact onAα(YI), there exist a functiong∈Aα(YI)and a subsequence of {fkj}(without loss of generality, still written by {fkj}), such that

LetEbe a compact subspace ofYI.For(Z,W)∈E, from Lemma 2.1 it follows that

|(Wφ,ufkj-g)(Z,W)|≤

(2)

From(2), we see thatWφ,ufkj-g→0 uniformly onEasj→∞.From this, for arbitraryε>0, there exists a positive integerN1such that

|u(Z,ξ)fkj(φ(Z,W))-g(Z,W)|<ε

(3)

for all(Z,W)∈E, wheneverj>N1.Sincefkj→0 uniformly onEasj→∞, also there exists a positive integerN2such that|fkj(Z,W)|<εfor all(Z,W)∈E, wheneverj>N2.

Let

N=max{N1,N2}

and

From(3), we have

|g(Z,W)|≤

(1+M)ε

(4)

for all(Z,W)∈E, wheneverj>N.From(4)and the arbitrariness ofε, we obtaing(Z,W)=0 for all(Z,W)∈E, which leads tog≡0 onYI.This shows that

which contradicts(1).

Now, assume that {fk} is a bounded sequence inAα(YI).Then it is locally uniform bounded onYI, which shows that there exists a subsequence {fkj} of {fk} such thatfkj→funiformly on every compact subset ofYIasj→∞.From this we havefkj-f→0 uniformly on every compact subset ofYIasj→∞.Consequently, we obtain

which shows thatWφ,uis compact onAα(YI).

In the studies of the several complex variables, the famous mathematician Hua found and proved the following so-called Hua’s matrix inequality in 1955:

Recently,Ref.[25]gives a generalization of Hua’s inequality inYI.

Lemma2.3LetK>0.For any two points(Z1,W1),(Z2,W2)∈YI，it follows that

Applying Lemma 2.3, we obtain some useful functions inAα(YI).

Lemma2.4Letα,K>0.For each fixed point(A,B)∈YI, the function

belongs toAα(YI), and

(5)

ProofFrom a direct calculation and Lemma 2.3, we have

From this, we obtainf(A,B)∈Aα(YI)and(5)holds.

3 The main results

Forφa holomorphic self-map ofYI, let(A,B)=φ(Z,W)for(Z,W)∈YI.

Theorem3.1Letα>0,K>0,φthe holomorphic self-map ofYIandu∈H(YI).Then the operatorWφ, uis bounded onAα(YI)if and only if

ProofAssume thatWφ,uis bounded onAα(YI).Then for eachf∈Aα(YI), there exists a positive constantCsuch that

‖Wφ,uf‖Aα(YI)≤C‖f‖Aα(YI)

(6)

For the fixed point(Z1,W1)∈YI，choose the function

where(A,B)=φ(Z1,W1).From Lemma 2.4, it follows thatf(A,B)∈Aα(YI).and ‖f(A,B)‖Aα(YI)≤1.By a direct computation, we have

|f(A,B)(φ(Z1,W1))|=

(7)

Then, applying the boundedness ofWφ,utof(A,B)along with(6)and(7), we have

‖Wφ,uf(A,B)‖≤C‖f(A,B)‖Aα(YI)≤C,

which shows that

MI=

+∞.

Conversely, by Lemma 2.1, for allf∈Aα(YI)we have

(8)

Hence, from(8)we see that the operatorWφ,uis bounded onAα(YI).The proof is end.

Next, we characterize the compactness of the operatorWφ,uonAα(YI).

Theorem3.2Letα>0,K>0,φthe holomorphic self-map ofYIandu∈H(YI).Then the operatorWφ,uis compact onAα(YI)if and only if

=0

(9)

ProofAssume that the operatorWφ,uis compact onAα(YI).Then it is clear that the operatorWφ, uis bounded onAα(YI).Consider a sequence {(Ai,Bi)}={φ(Zi,Wi)} inYIsuch that(Ai,Bi)→∂YIasi→∞.If such a sequence does not exist, then(9)obviously holds.Using this sequence, we define the function sequence

fi(Z,W)=f(Ai,Bi)(Z,W),

(Z,W)∈E=

{(Z,W)∈YI:dist(φ(Z,W),∂YI)<σ},

(10)

For suchεandσ, by using(10)and Lemma 2.1, we have

Since {(Z,W)∈YIE} is a compact subset ofYI,fi→0 uniformly on this set asi→∞.From this and(11)we get

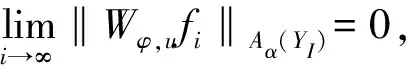
which shows that the operatorWφ,uis compact onAα(YI).

4 Conclusions

We study the weighted composition operators on Bers-type space of the first kind Cartan-Hartogs domain and characterize the boundedness and compactness by using the generalized Hua’s matrix inequality.