基于响应面分析的前大梁优化设计
2022-07-22吕喜敏
吕喜敏
华电重工股份有限公司上海分公司 上海 200120
0 引言
卸船机前大梁后端通过铰点由后大梁支承,中间位置通过拉杆支承。小车通过钢丝绳牵引在前大梁上往复运动完成工作。前大梁通常为箱形梁,即小车运行的轨道支承在一边腹板上,梁体由上下翼缘板及2块腹板围成长方形。箱形梁刚度高,抗扭及抗弯性能好,且质量轻,便于生产,广泛应用于港口机械领域。
作为承载小车的主要结构件,前大梁的自重对卸船机整体结构质量有重要影响。本文以1 500 t/h卸船机为例,利用Workbench创建前大梁的参数化模型,通过响应面优化法对大梁截面进行优化,减轻前大梁自重。
1 参数化模型的建立
如图1所示,前大梁由上下翼缘板、腹板等组成,大梁内部增加大隔板支承,并在盖板及腹板上增加纵向筋提高主梁的局部稳定性。前大梁后端由铰轴与后大梁相连,中间位置由大拉杆斜向上斜拉支承,2根前大梁端部由横梁连接。由于拉杆提供的拉力沿前大梁轴线方向有一定的分力,创建模型时要建立拉杆模型,使前大梁的受力更接近真实情况。前大梁中的纵向筋及隔板主要作用是提高盖板及腹板的局部稳定性,对前大梁的刚度及强度影响较小,在建模中可忽略,影响前大梁整体刚度和强度的参数主要是盖板及腹板的尺寸。
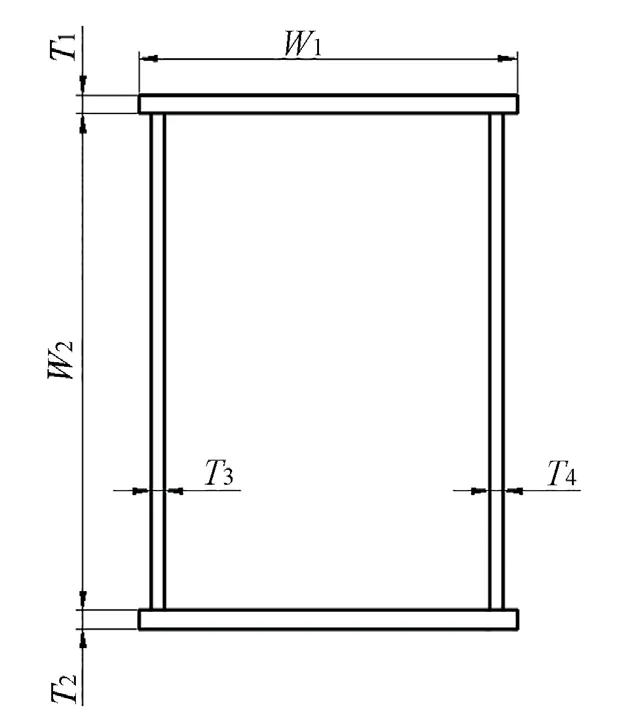
图1 前大梁截面图
基于以上分析,将影响结构强度及刚度的主要尺寸设置为参数,在Workbench中利用Beam 188单元创建前大梁的参数化有限元模型,该模型具有参数少、单元少、计算速度快、计算结果与实际情况相近等特点。
卸船机通常采用Q355B作为主结构材料,材料弹性模量E=2.06 GPa,泊松比μ=0.3。由于有限元模型中忽略了一些细节,使得材料密度需要进行调整才能保证前大梁的有限元模型自重与实际一致。对比后将材料密度设置为9 830 kg/m3,同时将一些质量较大部件以质量点的形式创建到模型中。调整Workbench中网格设置,选择合适的单元尺寸,创建图2所示前大梁有限元模型。

图2 前大梁有限元模型图
1.1 施加载荷及约束
根据前大梁实际安装方式,约束拉杆上端的3个位移自由度UX、UY、UZ,约束前大梁后端的3个位移自由度UX、UY、UZ以及2个旋转自由度ROTX、ROTZ。
前大梁的约束状态类似于带悬臂的简支梁,其最不利工况有2种,即小车位于最大前伸距位置时和小车位于2支点中间位置时,具体位置为距后大梁铰点1/1.732处[1]。针对2种工况进行静力分析,确定最不利工况。
1.2 静力学分析
分别分析小车位移最大前伸距以及拉杆铰点与后大梁铰点中间位置时前大梁的应力状态。小车位于不同位置时前大梁应力状态对比如图3所示。
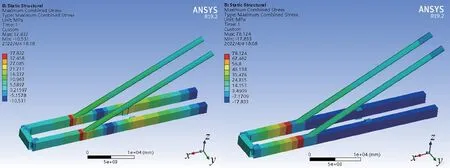
图3 小车位于不同位置时前大梁应力状态对比
根据F.E.M 1.001—1998 《欧洲起重机设计规范》要求[2],安全系数取1.5,前大梁材料为Q355B,则许用应力为
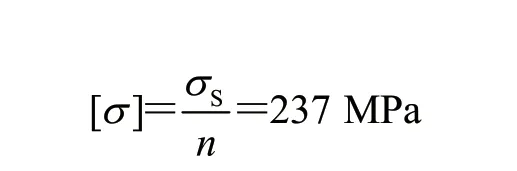
F.E.M 1.001—1998 《欧洲起重机设计规范》并未对变形做出要求,而当变形过大时会导致小车运行出现爬坡工况,对卸船机产生不利影响,根据GB/T 3811—2008 《起重机设计规范》要求,悬臂梁前端挠度不大于有效悬臂的1/350[3],即
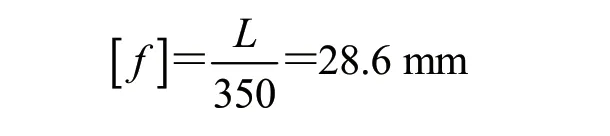
根据有限元分析结果,前大梁最不利工况为小车位于最大前伸距位置时,此时前大梁前端变形最大,为25.6 mm,前大梁在拉杆铰点处应力最大,为78.1 MPa,该前大梁的初始截面强度及刚度均满足要求,且具有一定的优化空间。
2 优化分析
结构参数的优化设计通常包括创建参数化模型、指定设计变量、指定目标函数、确定约束条件和找到最优解等。根据前述分析,将上下盖板及腹板的尺寸作为设计变量:上下盖板宽度W1初始值为1 300 mm,腹板高度W2为2 100 mm,腹板厚度T1、T2为10 mm,上下盖板厚度T3、T4为18 mm。将主梁质量作为目标函数,优化目标为质量最小。
根据F.E.M 1.001—1998 《欧洲起重机设计规范》以及 GB/T 3811—2008 《起重机设计规范》要求,设置约束条件:
1)根据工程实际经验,考虑卸船机使用时工况较为复杂,以及生产过程中的不可控因素导致的结构强度下降,采用Q355B时,应力通常控制在最大应力小于等于180 MPa;
2)根据GB/T 3811—2008《起重机设计规范》要求,有效悬臂处最大变形小于28.6 mm;
3)工程应用中要求主要结构件板厚不得小于8 mm;
4)前大梁翼缘板宽度与腹板高度比值大于1/3。
2.1 响应面分析
Workbench的Design Exploration模块提供了多种优化工具,其中的响应面(Response Surface)分析可以帮助设计人员确定输入参数对输出参数的影响,以便更快速精准地得出最优解。响应面分析会为每一个输出参数创建一个响应面,可以提供一个曲线或曲面图形来显示输出参数在一个时间点上如何随着1个或2个输入参数发生变化的。
对该方案增加设计样本点,样本点的优劣直接影响产生的响应面的精度[4]。Workbench提供了7种生成样本点的方法:1)中心组合设计法(Central Composite Design,CCD);2)空间填充设计法(Optimal Space-filling Design);3)设计法(Box-Behnken Design,BBD);4)用户自定义;5)自定义与抽样法(Custom+ Sampling);6)稀疏网格初始化法(Space Grid Initialization);7)拉丁超立方体抽样设计法(Iatin Hypercube Sampling Design)。
本文采用中心组合设计法生成样本点,中心组合设计法生成的样本点如图5所示。
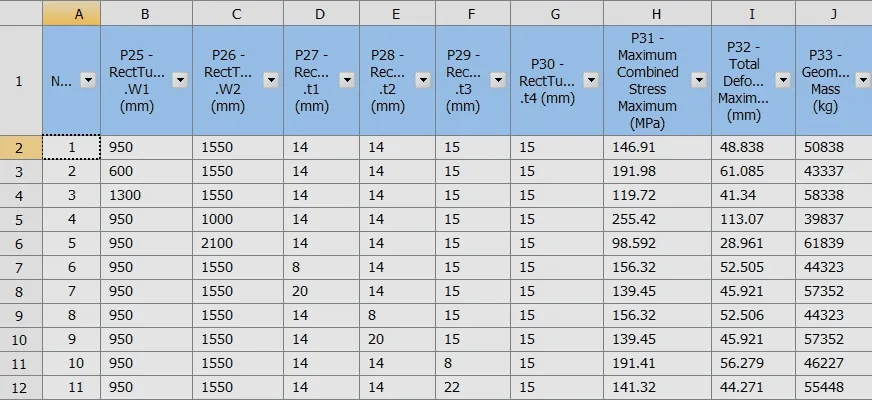
图5 中心组合设计法生成的样本点
Workbench创建响应面的方法有5种:遗传种群算法(Genetic Aggregation)、标准二阶响应面(Standard Response Surface-Full 2nd-Order Polynomials)、Kriging类型响应面(Kriging Algorithms)、非参数回归方法(Non-Parametric Regression,)和稀疏网格法(Sparse Grid)。通常采用标准二阶响应面,此响应面适用于输出参数变化较为缓和的情况。
图6为输入参数敏感度,各个输入参数对输出参数的影响不同,最大综合变形与最大综合应力对前大梁高度较为敏感,而前大梁质量对6个参数的敏感度相差不大。
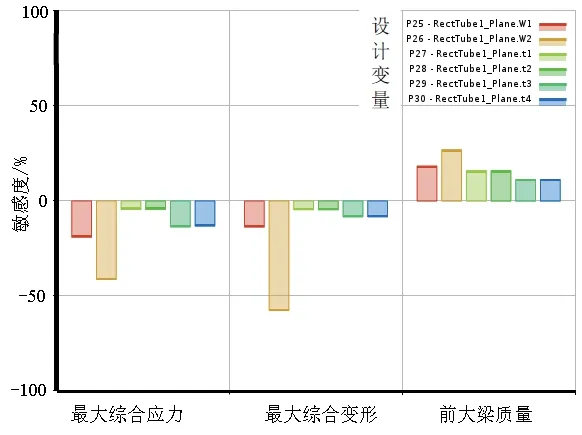
图6 输入参数敏感度
前大梁高度与宽度对最大综合应力的影响如图7所示,前大梁高度与宽度对最大综合位移的影响如图8所示。根据响应面分析结果可知,通过优化前大梁上下盖板宽度,可以在保持最大综合应力和最大综合变形不变的情况下,有效地减少前大梁自重。
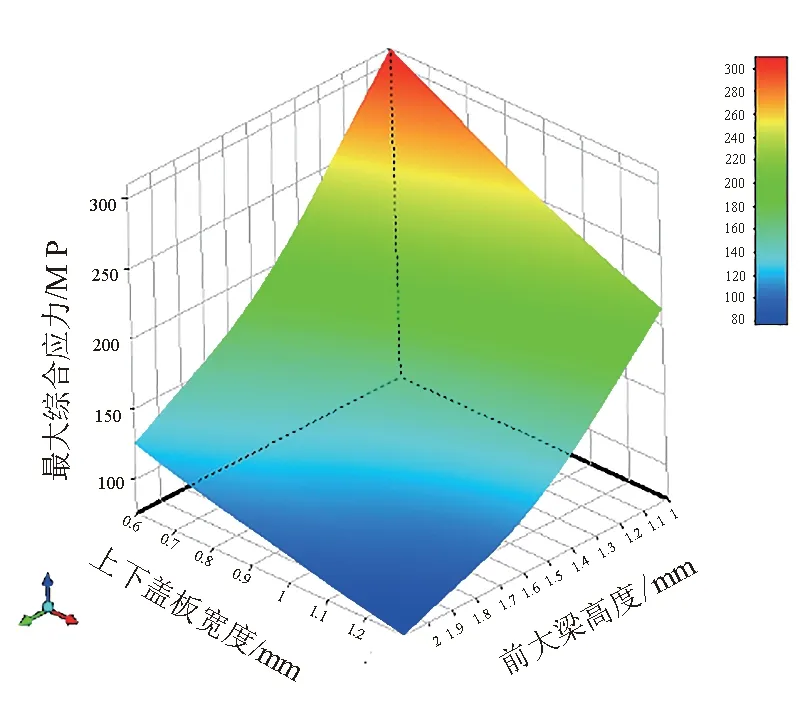
图7 前大梁高度与宽度对最大综合应力的影响
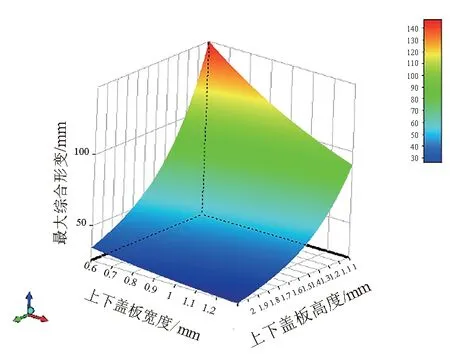
图8 前大梁高度与宽度对最大综合位移的影响
2.2 基于响应面的优化设计
以响应面分析结果为基础,采用单目标优化方法,对前大梁截面进行优化,得到3组候选点,根据3个候选点所给数据,从中找到最优设计点,并根据最优设计点数据修改有限元模型,进行静力学分析,得到优化后前大梁截面参数,优化前与优化后数据对比见表2。
由表2可知,优化后前大梁最大综合变形为28.5 mm,满足了GB/T 3811—2008 《起重机设计规范》要求,同时最大综合应力为95.2 MPa,满足F.E.M 1.001—1998 《欧洲起重机设计规范》要求。优化后的前大梁质量相比于优化前减少了15.5%,减重效果明显。
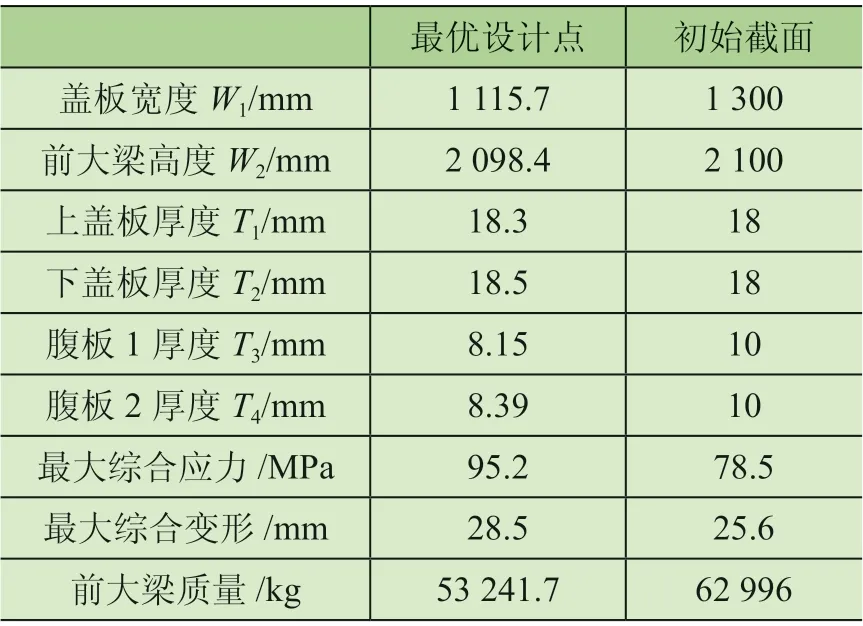
表2 优化前与优化后数据对比
3 结论
通过对前大梁进行静力分析,确定了前大梁的最不利工况以及相应的危险截面。在Ansys Workbench中创建前大梁的参数化模型,根据F.E.M 1.001—1998 《欧洲起重机设计规范》以及国内起重机设计规范建立约束条件,设置目标函数,并利用Workbench提供的优化设计模块Design Exploration进行响应面分析,得出各个参数对输出参数的影响,以响应面分析结果为基础进行优化分析,获得了一组满足约束条件的最优设计点,优化结果与初始设置相比,前大梁自重减少了15.5%,减重效果明显,为优化设计方法在实际工程场景中的应用提供参考。
