实现初中数学试卷讲评课高效的对策思考
2022-07-22林巧容



摘要:在新课程新理念下,追求课堂高效是教师的向往;在双减政策下,更是时代对教师提升教学效能的呼唤。试卷讲评课是初中数学教学的重要组成部分,是针对学生考试所反映出的错误进行矫正,是对缺漏和不足进行有效的干预,上好讲评课对夯实学生双基、矫正思维障碍、提升分析问题解决问题能力、培养学生创新意识等都有着特殊的意义。
关键词:合理定位;共性错误;思维能力
中图分类号:G633.6文献标识码:A文章编号:1673-8918(2022)24-0078-04
目前不少初中数学试卷讲评课存在低效或收获甚微的状态,比如,教师不顾主次,逐题讲解,眉毛胡子一把抓;没有合理归类,盲目重复操作,浪费学生的时间;重解题过程,轻方法指导,学生知其然而不知其所以然;面面俱到,一言堂,一讲到底,学生缺乏参与,老师讲得口干舌燥,学生听得昏昏欲睡;诸如此类,错失对学生学习品质提升的机会,严重挫败学生学习数学的热情,降低课堂实效。初中数学常见的试卷讲评课如何追求高效呢?仁者见仁,智者见智,笔者根据多年初中数学试卷讲评课的心得体悟,提出几点思考,以抛砖引玉。
一、 分析有效数据,合理定位,确定教学目标
优质的讲评课,备课是个庞大的工程。前期关注考场状态、成绩真实性,及时阅卷统分,进行本班横向和年段纵向比较,知晓本班这次考试成绩的整体情况,清楚各分数段人数的分布,细化到每题得分率(若统考可以利用好分数平台功能,查阅各种详细数据,发现学生薄弱环节,非常方便有效),包括典型的错误、思维障碍、奇思妙想等。针对试卷暴露出的问题,结合班情、学情,合理定位学生基础知识、基本技能和学习能力的情况,预测通过师生努力可以达到的水平,制定教学目标,使讲评重点突出,有效解决学生最突出、最主要、最想知道的问题,为后续的学习打下知识基础和提供能力保障。
以下是笔者送教下乡初三某班的一次试卷讲评课的案例。考试卷是《2020年漳州质检卷》。该试卷关注学生发展,突出能力,能有效区分学生的水平。如第8、11、14、23的第1小题等立足于考查学生对概念的理解和应用;第2、6、21题通过视图的观察、平移、旋转等几何变换对学生的空间观念进行考查;第13、19、22、24等题重点考查了高中必备的运算和推理能力;第7、22、23题通过创设与学生生活相关联的情景,考查学生的应用意识;第25题通过创新题型考查学生的创新意识。
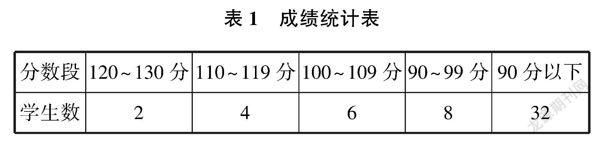
(一)成绩统计(见表1)
阅卷之后,跟该班数学任课老师进行了充分沟通,该校处城乡接合处,“留守学生”多,在高年级留守学生学习上两极分化现象尤其突出,部分学生有“读书无用论”的思想,学习上放弃了对自己的要求,基础薄弱,不思进取,思维欠缺,有16人属于这种状况,只做一点填空和选择题,分数在30分左右,3人有想读一点数学,无奈综合因素导致数学学习困难重重,这次测试成绩在50分之下。鉴于学生的实际情况和即将面临中考,针对这19名学生实施分层教学分层布置作业,课堂上特地设计一份数学托底训练练习,反复训练最基础的知识、最基本的技能,课后安排小老师一对一辅导,以达到数学课程要求——人人都能获得必需的数学,不同的人在数学上得到不同的发展。余下33位学生最低分64分,针对这33位学生的卷面完成情况,分析有效数据,合理定位,确定教学目标。
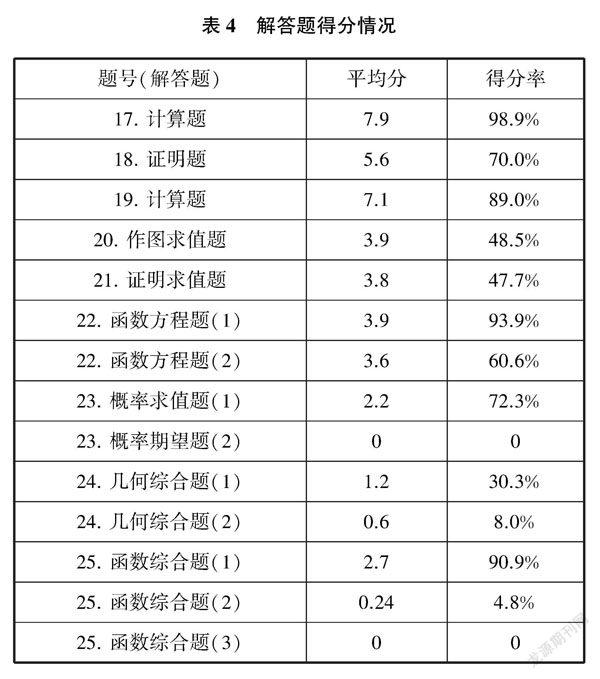
(二)试卷中各题得分情况(参与学生33人,见表2~表4)
分析表2~表4的有效数据统计,教学目标是托底和培优两头兼顾,合理定位,课堂锁定120分,像第23题第(2)题、第24题第(2)题、第25题第(2)(3)题无人会解或极个别学生解出部分的题目,课后个性化培优处理是注重不同层次学生的不同需求,尽量不浪费绝大部分学生的时间,提高教学实效。
二、 共性错误,归类剖析,提高课堂的实效
对知识的学习和掌握打一个比方:如果把知识比作一颗颗晶莹剔透的珍珠,学生比作拾珍珠的人,若粒粒散散的捧在手里,一装不了多;二肯定容易随时丢落。若用细绳把它们串联就能如愿获得所有珍珠。的确,知识也只有善于归类,才能使知识结构化、条理化、系统化,才有利于深层理解和有效掌握。类似地,老师在讲评课时,逐题孤立讲解,不仅费时、烦琐,而且失去让学生观察、类比、联想、转化等能力的培养机会,应该引导学生对试卷上多数的共性错误进行归类:是对概念、公式、法则、定理记忆不牢,理解不透,或理解错误?还是审题不严,对字、词、句解读有偏差?是计算没有根据算理算法出错,还是方法策略失当?针对错因,把相关联的题目归类,对症下药,在知识的整合和对比中,使学生对这类问题形成一个整体感,有助于学生有序、清晰地理解知识间内在关联,构建自身的新认知,也有利于知识持续生长和创新,为后续的学习提供不竭的动力,这才是真正的高效。
上面提到的送教下乡的试卷讲评课,根据试卷分析结果,绝大部分同学解答好的题目课堂不讲,共性、典型问题归五类剖析。先按知识内容归类:像第8、14、23(1)题涉及统计概率知识归为一类,重点回顾相关概念,并配以相应练习,鼓励学生这类题志在必得;像7、22题是中考必考的应用题归为一类,侧重复习应用题解题策略,如何找等量关系列方程,让学生对解应用题有自己熟练的方法;第18、20、21题是几何证明题归为一类,学生书写不规范、不严谨,推理能力薄弱,课堂上注重讲析几何证明的技巧——读题、标图、联想,同时拍照上传书写不规范的试卷,让学生辨析,避免重蹈覆辙;圆是很多学生头疼的内容,有些学生干脆遇圆绕道,自己心里先定位不會,但中考涉及圆的内容往往不是很难,像第8、24(1)题就是考查圆的相关知识归为一类,发现圆也没有那么难,目的在于激励学生不放弃;最后按试卷中的思想方法把第10、13、15、16题归一类讲析,它们分别应用了分类、整体、转化、数形结合等思想方法,让学生明白数学思想方法是数学的灵魂,时刻在用。分门别类之后课堂上创设民主、合作、探究的情景,通过师生互动、生生互动,引导学生答疑释疑、整合知识、总结方法规律、启迪思维,在紧凑、有序、愉悦中完成了教学任务。
三、 善用试卷中的好题,发挥学生的主体性,培养学生的思维能力
一遇难题,老师常感叹,类似的题目学生做过了、讲评过了,有时还多次做过、讲评过,考试依然很多学生不会,说明学生存在着思考缺欠甚至误区。老师讲评过的内容,囫囵吞枣,没有内化为自己的认知方式,学生的思维还停留在原有水平上。若试卷讲评课只是就题论题,相当于穿新鞋走老路,没有提升学生的思维水平,解题时难以跨越题目的思维障碍。史宁中教授在《数学教育的未来发展》中阐述过,数学教学应当承担起提升一个人未来思维能力的重担。因此,数学试卷讲评课只有承担起培养学生的思维能力的重担,方显出课堂的实效。
一份试卷常有个别题目很出彩,原型来自课本,不偏不怪不叼,有针对性和综合性,既考查多个知识点的联系,又渗透多种方法、策略和思想,难度适中,对学生又具有挑战性。老师要善于发现这种好题,发挥老师的主导作用,突出学生的主体地位,点拨学生一题多解,培养学生思维多样性和创新能力,在对比中总结思想方法;或变式拓展,牵引学生思维的发展和完善;也可以师生互换角色,共同探讨挖掘学生思维潜力等。在老师主导下,让学生去探索,大胆猜想、凝练观点、提出问题,唤醒创新意识,使学生真正成为讲评课的主人。在多角度、全方位的探索感知实践中,优化知识结构,培养思维能力,为后续学习助力,提升学生学习数学的核心竞争力。
笔者在评讲2019~2020学年第一学期九年级期中检测卷时,发现第16题就是典型好题。以下是笔者的处理方式,供大家批评指正。原题展现:已知菱形ABCD在平面直角坐標系中的位置如图1所示,顶点B(10,0),AC=85,点E的坐标是(0,2),点M是对角线AC上的一个动点,当MD+ME最短时,点M的坐标是。
分析点评:这是一道几何、代数综合题,涉及菱形、直角坐标系、一次函数、三角形相似等众多知识,综合考查学生整合知识熟练程度及分析问题、解决问题的能力。教学过程再现:师生共同互动分析几何解题套路——读题、标图、联想,所谓联想就是已知可知,未知还需要什么。引导学生回顾线段和最值策略“化同为异、化折为直”,学生发现这是两定一动模型,来自课本中的练习——两村在公路上建奶站问题。因此,只需作D或E关于AC的对称点,然后连接E或D与对称点交AC于一点M,即可确定M的位置。因为菱形是轴对称图形,点B、点D关于AC对称,所以连接BE交AC于点M,点M就是所求作的。如何求点M的坐标呢?老师点拨、引导学生一题多解,目的在于培养学生思维的多样性。请生1讲演思路,生1用函数知识解决问题:如图2,连接BD交AC于点F,因为四边形 ABCD 是菱形,所以AC⊥BD,AF=12AC=45,在 Rt△ABF 中,根据勾股定理求出BF=25,过点F作FN⊥AB,垂足为N,根据面积不变,12AF·BF=12AB·FN求出FN=4,在Rt△FAN中,根据勾股定理得AN=8,所以F(8,4),求出直线AC的解析式为y=12x,由B(10,0)、E(0,2)求出BE的解析式为y=-15x+2,联立y=12xy=-15x+2,解得x=207y=107,求得M207,107。请生2讲演思路,生2用三角形相似知识求解:如图3,过点M作MG⊥AB,垂足为G,因为四边形ABCD是菱形,所以AC⊥BD,所以∠AFB=90°,因为MG⊥AB,所以∠AGM=90°,得∠AFB=∠AGM,又由∠BAF=∠MAG,得△ABF∽△AMG,得BFAF=MGAG=2545=12,设MG=t,则AG=2t,易证△MGB∽△EAB,得MGAE=BGAB得t2=10-2t10,解得t=107,所以MG=107,AG=2t=207,得 M207,107。通过一题多解,变通求法,整合了知识结构,使一次函数、点的坐标、菱形、三角形相似等知识有机融合在一起,生成为学生的新认知。教师还可以跟学生互换角色,拓展外延,激发学生思考,如追问:刚才是在菱形的背景下考了两定一动模型,还可以考什么呢?请学生出题。学生根据学习经验回答,可以考一定两动模型。请生3出题:如图4,在AC、AB上找点M、G,使MG+MB最短,求点M的坐标。师解答分析:解题策略相类似,还是“化同为异,化折为直”,连接MD,根据菱形的对称性,得MD=MB,所以要求MG+MB最短,只需求MG+MD最短,由“垂线段最短”原理,过点D作DG⊥AB,垂足为G,则DG交AC于点M,这时点M就是所求作的点。
四、 课后跟进落实,端正学习态度,培养学习习惯
双减政策下,课堂45分钟是老师的主阵地。为了课堂提质增效,不浪费绝大多数学生的时间,试卷讲评课无法当堂解决所有学生的所有问题,个别学生的不具有代表性的问题要求学生课外自行订正,积极主动地寻找解决办法,并做好错因分析说明,课后老师要一一落实问题解决情况,让学生的错误不留死角,培养学生有错必究的良好习惯,形成积极主动解决问题的态度。课后根据讲评课反馈的情况,布置3、4道作业进行刻意学习,巩固最重要的知识技能,为后续学习打下坚实的知识基础。
在试卷讲评课中,忌讳面面俱到、平均使力,应该以恰当的方式,抓住学生问题的“要害点”,抓准学生思维提升的“盲点”,在学生最近发展区做精辟的演绎,引领学生从纷繁复杂的内容中理清头绪,抓住问题的本质,突破难点,这才是真正的追求高效。把握好“讲”与“不讲”、“讲多”与“讲少”、“精讲”与“多练”教学节奏,优化课堂,为学生的思考提供足够的时间和空间,把学习的主动权还给学生,使学生在主动、积极的情感状态下掌握知识和技能,培养分析问题和解决问题的能力。
参考文献:
[1]韩新正.谈数学课堂教学的节奏之美[J].中小学数学,2013(9).
作者简介:林巧容(1975~),女,汉族,福建宁德人,福建省宁德市蕉城区蕉城中学,中学一级教师,研究方向:初中数学。
