基于GRACE和GRACE-FO的黄河流域陆地水储量及影响因素分析

任立良，王 宇，江善虎，卫林勇，王孟浩，张怡雅

(1.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学水文水资源学院，江苏 南京 210098)

黄河流域是我国重要的生态屏障区和经济发展区[1]。黄河流域上游水资源利用效率和经济水平较低；中游水土流失严重，生态系统脆弱，水资源污染严重；下游用水需求大，水资源浪费严重[2-4]。受气候变化和人类活动双重影响，流域水循环过程发生了显著变化，水资源保障形势愈发严峻，研究变化环境下黄河流域水资源演变特征对黄河流域生态保护和高质量发展具有重大意义[5-6]。陆地水储量(terrestrial water storage, TWS)变化综合反映区域地表水、地下水以及河流湖泊水的变化，是衡量地区水资源变化的重要指标。由美国国家航空航天局和德国航空航天中心联合开发的GRACE(gravity recovery and climate experiment)卫星计划是监测大尺度TWS变化的有效方法。自2002年3月GRACE卫星发射以来，GRACE卫星数据被广泛应用于研究陆地冰川消融、海平面与环流变化、干旱监测和TWS监测等[7-10]。张璐等[11]基于GRACE卫星遥感数据，发现黄河流域2003—2015年多年平均TWS西多东少，呈下降趋势，其上游主要受降水和蒸散发的影响，中、下游受人类活动影响较大；李晓英等[12]发现黄河流域2003—2016年TWS变化呈下降趋势，同一时段径流对TWS变化的影响最直接，考虑时滞性，降水主要受森林、农田扩大，植被的叶面积指数和蒸散发增大的影响；Li等[13]发现2003—2016年黄河流域中、下游南部TWS下降幅度最大。GRACE卫星遥感数据截止到2017年6月，后续由GRACE Follow-On (GRACE-FO)卫星接替，GRACE-FO卫星遥感数据从2018年5月更新，两个卫星遥感数据之间存在约1 a的数据缺失，不利于研究TWS长时间序列变化特征。针对这一问题，不同学者采用不同方法填补这一数据缺失，Sun等[14-15]采用深度神经网络、BP神经网络和径向基函数神经网络来填补GRACE与GRACE-FO间的数据缺失。

本文采用长短期记忆(long short-term memory, LSTM)神经网络模型，重建GRACE和GRACE-FO间的TWS变化量，研究黄河流域2002年4月至2020年3月长时间序列TWS，分析气候因子与TWS变化的相关性，为黄河流域水资源管理和利用提供科学依据，并为其他流域的TWS研究提供参考。

1 研究区概况和数据来源

1.1 研究区概况

黄河流域位于95°E～119°E、32°N～41°N之间，流域面积约79.5万km2，地势自西向东逐级下降(图1(a))，流域横跨青藏高原、内蒙古高原、黄土高原以及华北平原，流经青海、四川等9个省级行政区(下称省区)。黄河流域2003—2016年平均TWS西部高、东部低，空间差异显著(图1(b)，图中TWSA(terrestial water storage anomaly)为TWS的距平值，即为遥感TWS数据减去2004—2009年的月平均值)。2003—2019年流域降水量分布不均，从东南向西北递减，降水集中在夏秋季节(图1(c))；流域蒸发能力很强，东南部蒸散发量大于西北部(图1(d))，最大蒸散发出现在7—8月，此时对TWS影响最大[16]。

(a) 高程

1.2 数据来源

1.2.1GRACE数据

GRACE数据主要由美国德克萨斯大学空间研究中心、美国太空总署喷气动力实验室和德国波茨坦地球科学中心3家科研机构对其进行解算和发布[17]。本文选取了2002年4月至2020年3月GRACE/GRACE-FO CSR RL06 Mascon V2产品TWSA，时间分辨率为1月，空间分辨率为0.25°。GRACE缺失数据是由于①GRACE卫星传感器等问题导致某些月份数据缺失；②GRACE和GRACE-FO间存在数据缺失，时间跨度为2017年7月至2018年5月。本文采用六点样条插值法填补GRACE卫星缺失月份数据，并利用LSTM填补GRACE和GRACE-FO间连续11月TWS变化量数据缺失，用于分析2002年4月至2020年3月黄河流域TWS的变化特征。

1.2.2GLDAS数据

全球陆面数据同化系统(global land data assimilation system, GLDAS)由美国航空航天局戈达德空间飞行中心和美国海洋与大气局国家环境预报中心共同开发完成。GLDAS包括Noah、VIC(variable infiltration capacity)、CLM(community land model)、Mosaic等4个模型，通过汲取遥感卫星观测数据和地面观测数据，输出全球地表状态通量及变量数据[18]。本文采用最高空间分辨率为0.25°的Noah陆地表面模型，时间尺度为2002年4月至2020年3月，与GRACE/GRACE-FO CSR RL06 Mascon产品数据相匹配，并选取了Noah陆地表面模型中的雪水当量、土壤水分(土壤深度分别为0～10 cm、10～40 cm、40～100 cm、100～200 cm)和冠层水数据，累加得到GLDAS的TWSA。

1.2.3降水量和气温数据

本文采用中国气象局发布的2002年4月至2020年3月黄河流域降水量和气温数据，分别来自中国地面降水月值(China gauge-based monthly precipitation analysis product, CPAP)0.5°×0.5°格点数据集V2.0和中国地面气温月值0.5°×0.5°格点数据集V2.0，时间分辨率为1月，降尺度为0.25°。

1.2.4蒸散发和径流数据

本文蒸散发和径流数据来源于Noah模型2002年4月至2020年3月的模拟结果，空间分辨率为0.25°，蒸散发数据时间分辨率为1 s，径流数据时间分辨率为3 h，经累加计算将时间分辨率转换为1月。

2 研究方法

2.1 LSTM神经网络模型

LSTM模型通过改进隐藏层内部结构获得长期记忆样本数据中的历史重要信息，解决了传统循环神经网络随训练时间加长或网络层数增多引起的梯度爆炸或消失问题。LSTM单元中引入了输入门(控制当前时刻神经单元的输入)、遗忘门(以一定的概率控制上一时刻以及单元历史信息的存储)和输出门(控制当前时刻记忆单元的信息输出)，能较为准确地预测时间序列。Wei等[19]采用LSTM模型，结合GLDAS地表水、累积降水、气温数据重建了柴达木盆地GRACE和GRACE-FO间的缺失数据，研究了柴达木盆地TWS的时空变化特征及其原因。目前大多学者利用人工神经网络重建的输入层均采用降水、气温、蒸散发和GLDAS地表水等数据，直接模拟GRACE和GRACE-FO间的缺失数据。本文将GRACE和GRACE-FO卫星数据反演与GLDAS和水量平衡方程计算的TWS变化量作为输入变量，采用LSTM模型重建黄河流域GRACE和GRACE-FO间的TWS变化量，反推GRACE和GRACE-FO间的缺失数据。

2.2 TWS变化量计算方法

基于GRACE和GRACE-FO卫星数据反演和LSTM模型重建的逐月TWSA序列，计算逐月TWS变化量时间序列[20]：

(1)

式中：CSt为流域t月的TWS变化量；ST,t+1、ST,t-1分别为t+1月和t-1月的TWSA。

基于GLDAS蒸散发及径流数据，结合CPAP月降水数据，利用水量平衡方程计算黄河流域TWS变化量：

CSt=Pt-Et-Rt

(2)

式中Pt、Et、Rt分别为t月流域平均降水量、蒸散发量和径流深。理论上，式(1)(2)得出的TWS变化量是相等的，因此，采用由水量平衡方法得到的TWS变化量来评估LSTM模型计算得到的TWS变化量是可行的。

2.3 地下水储量计算方法

流域TWS包括地表水储量、土壤水储量和地下水储量。为进一步分析流域TWS变化量的子成分，需对黄河流域地下水储量进行计算，计算公式[21]为

SG=ST-SSM-SSW-SCI

(3)

式中：SG为流域地下水储量；ST为流域TWS；SSM为流域土壤水储量；SSW为流域雪水当量；SCI为流域冠层水储量。

2.4 Spearman秩相关系数法

Spearman秩相关系数法常用于分析两个变量之间关系的密切程度，计算公式为

(4)

3 结果与讨论

3.1 GRACE和GRACE-FO间TWS变化量重建效果验证

利用GRACE(2002年5月至2017年5月)和GRACE-FO(2018年7月至2020年2月)卫星数据反演的连续201月TWS变化量时间序列测试LSTM模型对TWS变化量的模拟效果，随机抽取190月数据作为训练样本，剩余11月数据作为验证样本，结果如图2所示。训练期的Spearman秩相关系数为0.93，纳什效率系数为0.87，标准化均方根误差为0.06(图2(a))；验证期的Spearman秩相关系数为0.95，纳什效率系数为0.83, 标准化均方根误差为0.12(图2(b)),表明LSTM模型对TWS变化量模拟性能良好，可用于重建GRACE和GRACE-FO间TWS变化量。

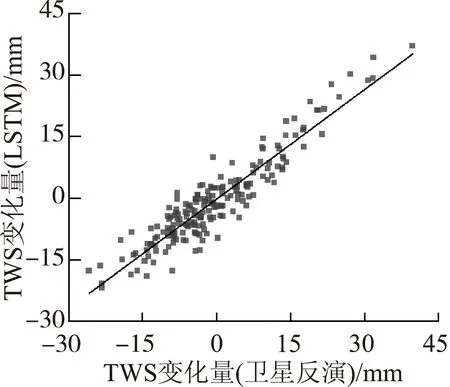
(a) 训练期

GRACE和GRACE-FO卫星数据反演和LSTM模型重建的黄河流域2002年5月至2020年2月区域平均TWS变化量在月尺度上的变化过程如图3(a)所示，与GLDAS和水量平衡方程计算结果相比可以发现三者的变化趋势非常相似，峰值所处的时间段相近。如图3(b)所示, 卫星反演和模型重建的TWS变化量与水量平衡方程计算结果的Spearman秩相关系数在GRACE时期为0.64、数据缺失时段为0.75、GRACE-FO时期为0.73、研究期为0.65；如图3(c)所示，卫星反演和模型重建的TWS变化量与GLDAS计算结果的Spearman秩相关系数在GRACE时期为0.73、数据缺失时段为0.86、GRACE-FO时期为0.73、研究期为0.72。Spearman秩相关系数均通过了p<0.01的显著性检验，比较结果验证了LSTM模型重建GRACE和GRACE-FO间TWS变化量的可靠性。

图3 TWS变化量在月尺度上的变化趋势和相关性分析

水量平衡方程计算TWS变化量时只考虑了气候因素的影响，而GRACE卫星遥感数据受人类活动的影响，两者之间有一定的差异，且GRACE卫星遥感数据对于TWS亏损更加敏感。而GRACE卫星遥感数据和GLDAS得到的TWS变化量包含的水文变量不一致，GRACE卫星遥感数据包含了地下水和湖泊水等，两者之间也存在一定差异性。

3.2 TWS趋势分析

利用TWSA对TWS进行趋势分析，图4为黄河流域2002年4月至2020年3月的TWSA在月尺度上变化趋势。从图4可以看出，全流域TWSA呈下降趋势，下降速率为-0.40 mm/月；上游TWSA呈平缓下降趋势，下降速率为-0.16 mm/月；中游TWSA呈缓慢下降趋势，下降速率为-0.67 mm/月；下游TWSA呈急剧下降趋势，下降速率为-1.83 mm/月，表明黄河流域TWS空间差异显著。由于黄河流域降水、气温、蒸散发等气候因子具有季节性变化特征，TWS也表现出明显的季节性变化特征，旱季TWS一般处于亏损状态，湿季TWS一般处于盈余状态。

图4 TWSA在月尺度上的变化趋势

如图5所示，黄河流域2003—2019年多年月均TWSA、降水量、蒸散发量和气温均呈现明显的季节性变化，黄河流域降雨集中在夏秋季节，多年最小月均TWSA和最大月均TWSA分别出现在6月和10月。6月之前雨季还未来临，气温高，蒸散发量大，TWSA最低；7—8月降雨集中，TWSA逐渐增大，蒸散发量达到了最大值；TWSA峰值出现在10月，滞后降水量的峰值约2月。

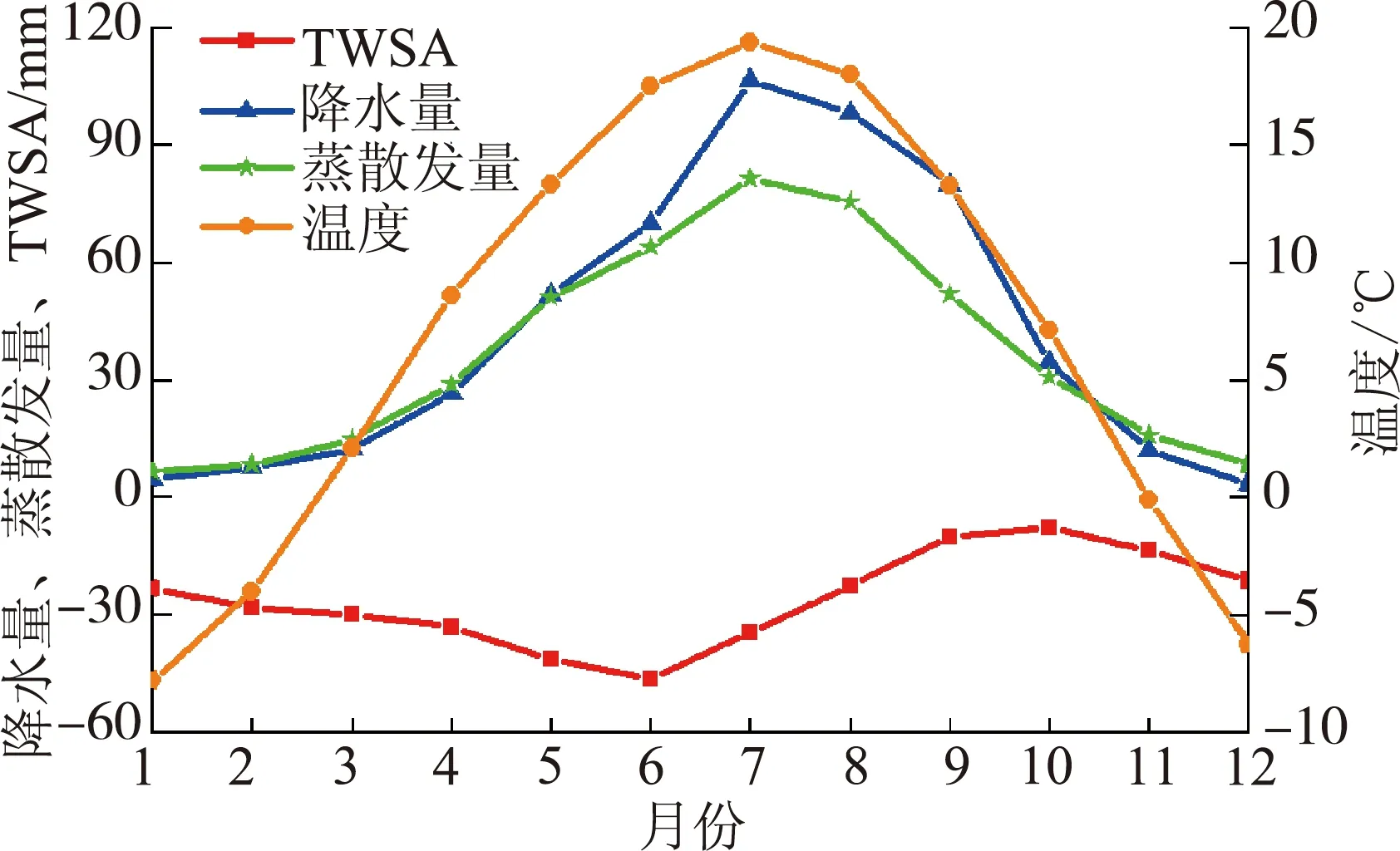
图5 2003—2019年各变量多年月均值

3.3 TWS各成分分析

图6为黄河流域TWS各成分时间变化趋势图。从图6可以看出，土壤水储量以0.12 mm/月的速率平缓增长；雪水当量和冠层水储量以0.001 8 mm/月的速率呈不明显增长的趋势；而地下水储量以-0.52 mm/月的速率急剧下降，与TWSA变化速率-0.40 mm/月相近。

图6 TWS成分在月尺度上的变化趋势

对黄河流域年TWSA和年地下水储量的相关性分析发现TWSA以-5.34 mm/a的速率下降，地下水储量以-6.48 mm/a的速率快速下降，两者变化趋势相似。涂梦昭等[22]研究发现，黄土高原2005—2014年地下水储量整体上以(-6.5±0.7) mm/a的速率急剧下降，与本文结果相近。年TWSA和年地下水储量的Spearman秩相关系数为0.90(p<0.01)，两者呈极显著相关性，表明黄河流域TWS的急剧下降与地下水储量急剧下降有关。

3.4 TWS影响因素分析

TWS受气候因素和人类活动影响，本文基于2002年4月至2020年3月数据，重点分析气候因素对TWS的影响。图7为黄河流域TWS变化量与降水量和干燥度指数在年尺度上的变化关系。从图7可以看出，年降水量上游和中游呈上升趋势，下游呈下降趋势；年干燥度指数上游呈下降趋势，中游和下游呈上升趋势。黄河流域上、中、下游年TWS变化量与年降水量和年干燥度指数分别呈极显著的正相关关系和负相关关系，上、中、下游年TWS变化量与年降水量的Spearman秩相关系数分别为0.79、0.89和0.71；上、中、下游年TWS变化量与年干燥度指数的Spearman秩相关系数分别为-0.74、-0.93和-0.77，表明降水和蒸散发是黄河流域TWS变化量的重要影响因素。除气候因素以外，人类活动(水库调度、工农业用水等)对黄河流域TWS有较大影响[16]。

(a) 上游

4 结 论

a.基于LSTM模型重建GRACE和GRACE-FO间TWS变化量是可靠的，其与GLDAS和水量平衡方程计算的TWS变化量的相关系数分别为0.65和0.72。

b.研究期间，黄河流域TWSA分别以-0.40 mm/月和-5.34 mm/a的速率下降，上、中、下游TWSA分别以-0.16 mm/月、-0.67 mm/月和-1.83 mm/月的速率下降，表明黄河流域TWS变化空间差异显著。TWSA最小值出现在6月，最大值出现在10月。黄河流域地下水储量以-6.48 mm/a的速率快速下降，TWSA的急剧下降很可能是地下水急剧下降导致的，两者的Spearman秩相关系数为0.90。

c.黄河流域上、中、下游年TWS变化量与年降水量和年干燥度指数分别呈极显著的正相关关系和负相关关系。上、中、下游年TWS变化量与年降水量的Spearman秩相关系数分别为0.79、0.89和0.71；上、中、下游年TWS变化量与年干燥度指数的Spearman秩相关系数分别为-0.74、-0.93和-0.77，表明降水和蒸散发是黄河流域TWS变化量的重要影响因素。