考虑摩擦剥落故障的直齿轮副啮合刚度研究

许礼进 陈青

(埃夫特智能装备股份有限公司，安徽芜湖, 241060)

0 引言

齿轮传动因其瞬时传动比恒定，故具有传递功率范围广、效率高、寿命长等优点，已被广泛应用于传动机构中[1]。时变啮合刚度作为渐开线直齿轮副传动过程中主要的动态激励源，是齿轮系统动力学特征的重要基础参数[2]。但在齿轮副传动过程中，轮齿由于受到疲劳磨损和热应力载荷作用，伴随冷焊现象的产生，常常出现齿面点蚀和剥落缺陷，对齿轮副时变啮合刚度影响较大，严重时会导致齿轮副传动失效[3]。

国外众多学者对直齿轮副齿面点蚀剥落故障研究较多，且分别讨论了矩形剥落、圆形剥落、V字形剥落和椭圆形剥落对齿轮副时变啮合刚度影响[4-6]。相比而言，国内对剥落故障研究较少，且所采用的剥落区域大都是沿齿轮轴向中心面对称。对于齿面剥落故障，在工程实际中，由于齿轮副和传动轴的安装误差，导致齿轮在传动过程中发生轴向和径向振动，并且在齿轮啮合热应力作用下，发生非对称性的点蚀剥落[7]。对于齿轮副齿面摩擦的研究，Saxena[8]等人研究了定摩擦因数对直齿轮时变啮合刚度的影响规律，并且将齿轮简化为基圆加悬臂梁模型，研究了齿面摩擦作用下直齿轮副的时变啮合刚度特征；杨勇[9]等人建立了计及齿面摩擦因数的直齿轮啮合刚度计算模型，分析了不同摩擦因数下齿轮时变啮合刚度特征。综上所述，现有的研究大都是考虑单一因素对啮合刚度影响，而且对于齿面摩擦，大部分采用定摩擦因数，忽略了齿面摩擦因数的时变特性，而且将齿面摩擦和齿面剥落故障综合考虑的研究较少。

本文以矩形剥落故障直齿轮副为研究对象，以对称剥落区域和非对称剥落区域为基础，建立剥落故障和齿面摩擦模型，研究不同偏心剥落及齿面时变摩擦对齿轮副啮合刚度的综合影响，推导齿面摩擦和剥落故障共同作用时齿轮副啮合刚度解析计算模型，为研究剥落故障直齿轮副啮合传动动力学特征提供理论基础。

1 剥落故障齿轮副时变啮合刚度

1.1 对称剥落

当齿轮副发生齿面剥落故障时，因为高速齿轮的齿数较小，容易发生点蚀剥落故障。在齿轮副的啮合传动过程中，其发生齿面点蚀剥落概率最大的是在单啮合区间内。

为简化计算模型，假定剥落区域为矩形，并位于主动轮节圆位置处，沿着齿轮轴向中心面对称，图1给出剥落区域的长度as，宽度bs和剥落深度hs。图2给出齿轮副啮合刚度计算悬臂梁模型，图中Ra、Rf、Rb、R分别表示齿顶圆半径、齿根圆半径、分度圆半径和分度圆半径，L和h为齿宽和齿高，a1和a2表示齿轮副在啮合点的压力角和一个轮齿对应中心角的一半，as和ax表示剥落故障上边缘和下边缘所对应的压力角，Fa和Fb表示等效啮合力F分解后的径向压缩力和剪切力，x为实际啮合点距基圆的径向距离，hx表示实实际啮合点距轮齿中心线OP的距离。

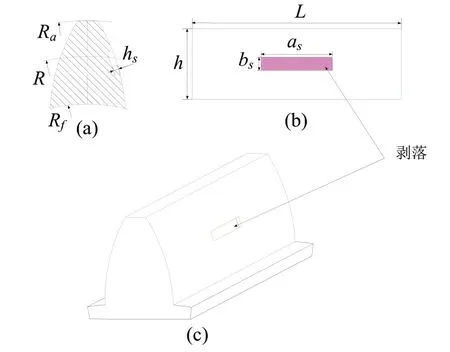
图1 剥落故障示意图

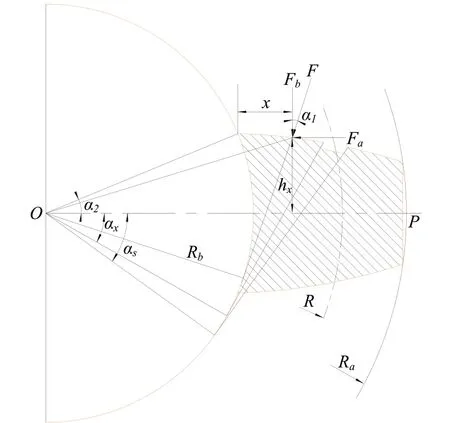
图2 悬臂梁模型

根据对称剥落齿轮副啮合刚度的研究，当齿面发生剥落时，会改变轮齿的弯曲刚度kb、剪切刚度ks和径向压缩刚度ka，改变后的计算模型如公式（1）-公式（3）。其他刚度分量计算见参考文献[10-12]。

剥落处弯曲刚度：

剥落处剪切刚度：

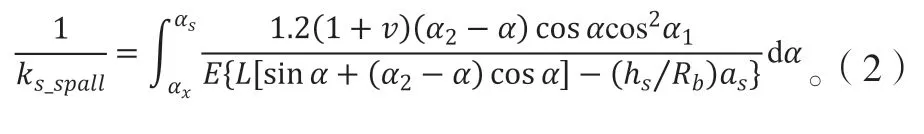
剥落处径向压缩刚度：

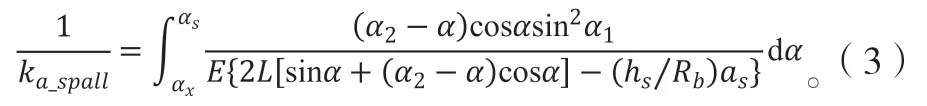
其中，E和v为齿轮材料的弹性模型和泊松比。

表1所示为齿轮副主要参数，取as=4mm，bs=8mm，hs=0.2mm，利用Sainsot[13]提出的对称剥落计算模型，计算得到对称剥落齿轮副时变啮合刚度如图3所示。

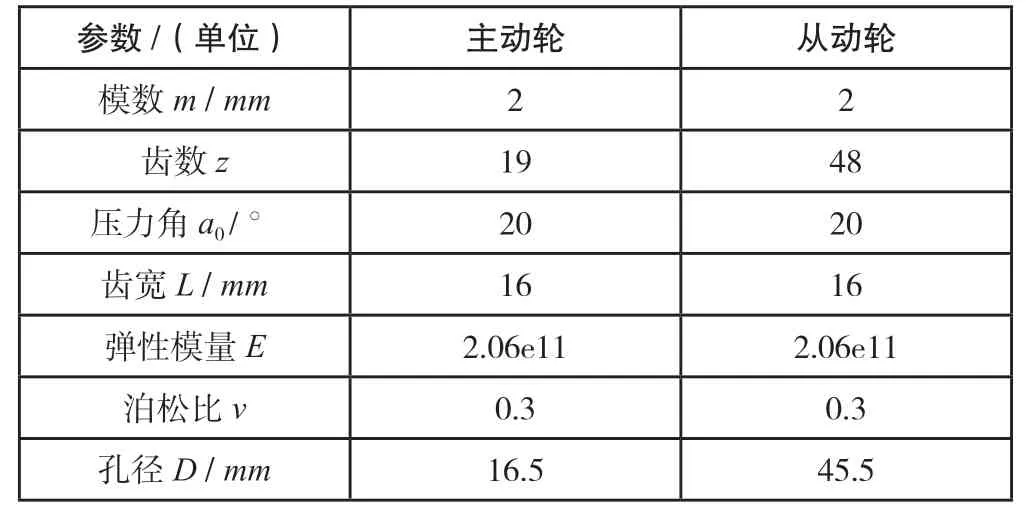
表1 直齿轮副主要参数

图3 对称剥落齿轮副时变啮合刚度

1.2 偏心剥落

由于传动轴及齿轮副存在制造和安装误差，导致传动过程中齿轮发生轴向和径向振动，使齿轮齿面轴向受力不均，以及传动轴简支梁受力产生弯曲变形，使得剥落区域并不沿着齿轮轴向中心面对称。在实际工程应用中，轮齿齿面发生点蚀剥落情况较为复杂，所以考虑到的是非对称性的齿面剥落。如图4所示，剥落区域仍位于主动轮节圆位置处，其剥落的偏心量为ls。

由于剥落区域不是沿齿轮轴向中心面对称，齿间分布载荷分布不均匀，剥落轮齿会产生扭转变形，进而产生扭转刚度kt，其他刚度分量保持不变。使用等效作用力Ftotal和等效作用力矩T代替齿面的分布载荷F，如图5和图6所示。

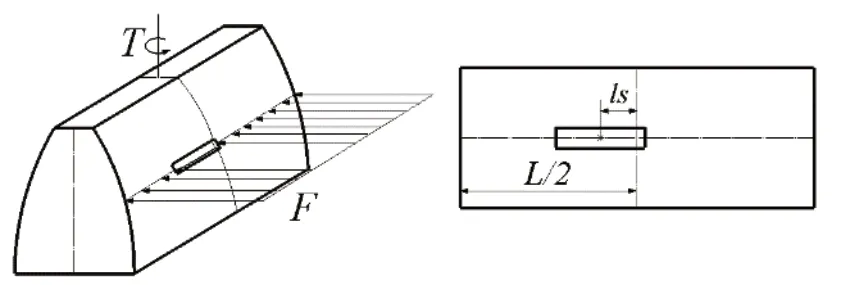
图4 非对称点蚀剥落

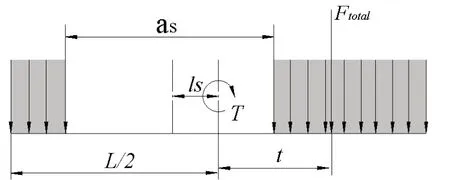
图5 剥落区域两侧载荷分布

图6 剥落区域两侧载荷分布

下面根据势能法推导剥落齿轮副轮齿扭转刚度。

扭转势能：

其中，t为等效作用力臂，G为材料剪切模量，lpx为轮齿极惯性矩。

按照图5和图6，将齿间载荷利用Ftotal等效后，其作用力臂t由式（5）计算：

极惯性矩Ipx为：

由此可化简得到剥落区域产生的扭转刚度为：

根据相互作用力，与剥落轮齿相啮合的从动轮健康轮齿扭转刚度为：

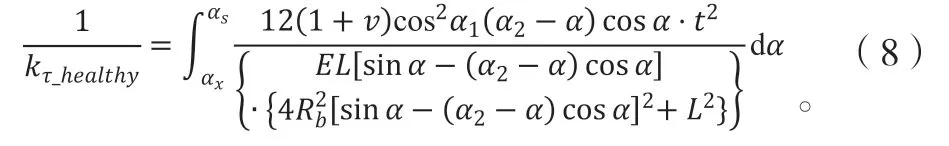
当剥落区域在单齿啮合区间时，齿轮副啮合刚度为：

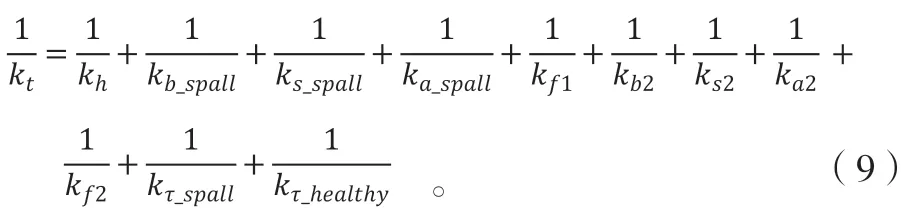
当剥落区域在双齿啮合区间时，齿轮副啮合刚度为：

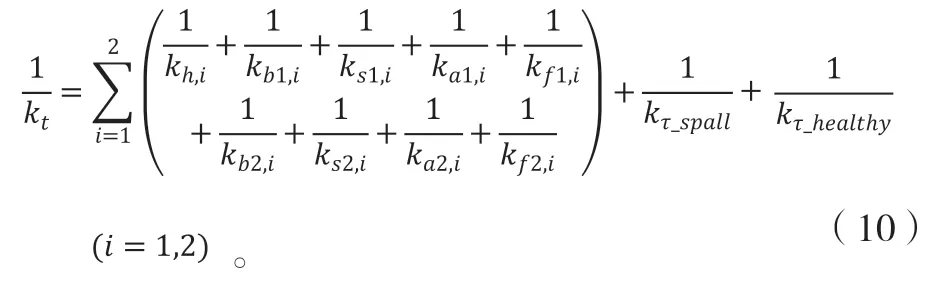
选取齿轮副主要参数参照表1，选取不同的剥落偏心量参照表2，在考虑因偏心剥落产生的扭转刚度后，计算剥落齿轮副啮合刚度，得到偏心剥落齿轮副时变啮合刚度及主动轮、从动轮的扭转刚度如图7、图8和图9所示。

表2 偏心剥落区域参数

图7 偏心剥落齿轮副时变啮合刚度

图8 偏心剥落齿轮副主动轮扭转刚度

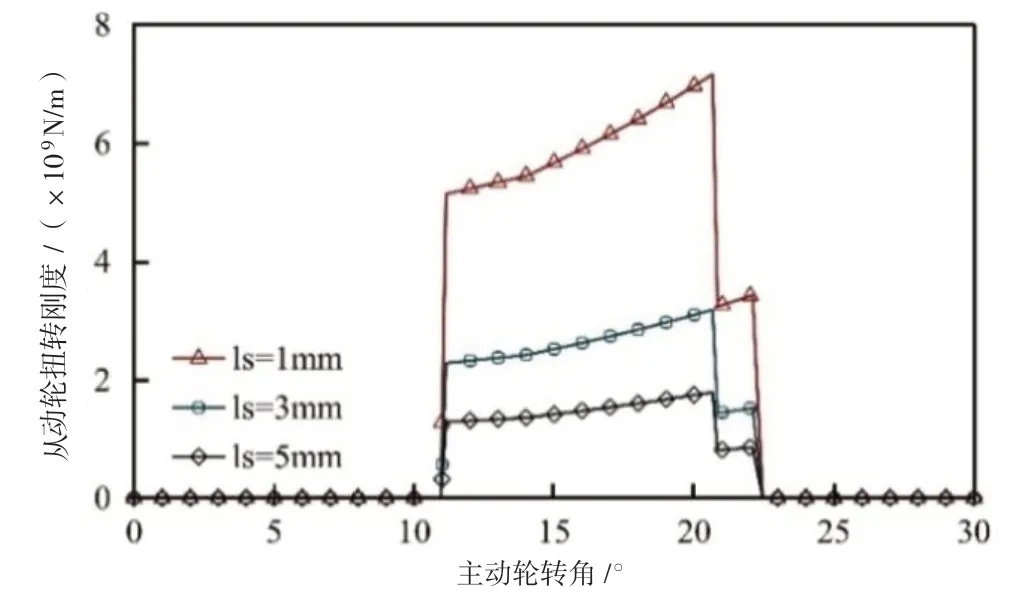
图9 偏心剥落齿轮副从动轮扭转刚度

可以看出，当剥落区域沿齿轮轴向中心面不对称时，剥落轮齿产生扭转刚度，会进一步减小直齿轮副的时变啮合刚度，并随着剥落区域偏心量的增大，剥落轮齿的扭转刚度和齿轮副啮合刚度呈现出减小的趋势 。由于主动轮的齿厚较大，其剥落区域产生的扭转刚度要远远大于与之相啮合从动轮健康轮齿扭转刚度。在实际工程应用中，应尽量减小齿轮副及传动轴的制造和安装误差，以减小发生剥落故障时的偏心量，增大啮合刚度，延长齿轮副使用寿命。

2 考虑摩擦的剥落齿轮副啮合刚度

在直齿轮副传动过程中，因为齿面摩擦力和热应力载荷，使得齿面发生点蚀剥落缺陷，可见齿面摩擦因素对齿轮副啮合刚度影响较大。本节考虑齿面摩擦的因素，研究其与点蚀剥落对啮合刚度的综合影响。

2.1 定齿面摩擦与点蚀剥落

在齿轮副传动过程中，齿面摩擦的大小及方向随齿轮啮合参数呈现出时变的特性，本小节仅考虑定摩擦因数下剥落缺陷齿轮副的时变啮合刚度。图10为从动轮一个轮齿啮合传动啮入阶段和啮出阶段的摩擦力方向示意图，其摩擦力方向随齿轮副啮合过程时变，但始终与齿廓相切，且指向啮合节点。根据此特点，可建立摩擦力对剥落齿轮副啮合刚度影响的模型。图中，和表示主动轮和从动轮的角速度，取主动轮啮入阶段和啮出阶段任意啮合点A和B， 表示啮合点的压力角，f为摩擦系数，Ff为齿间摩擦力。

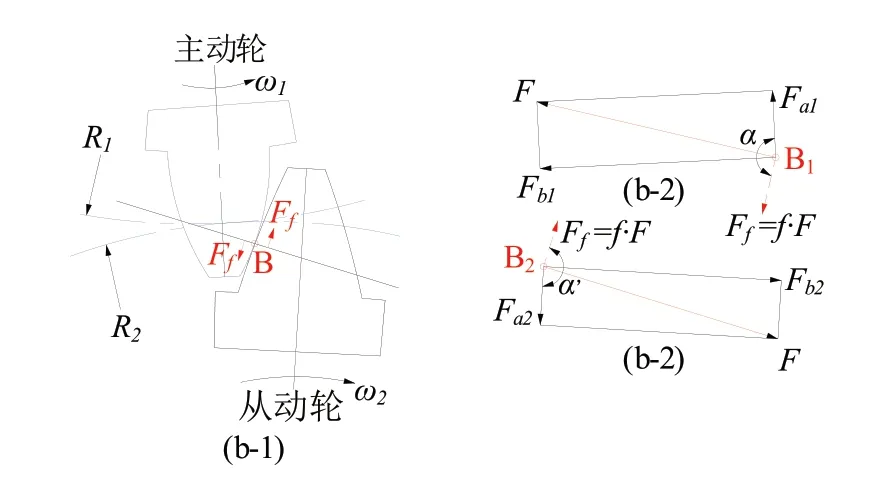
图10 啮合过程中摩擦力方向示意图

根据对齿面摩擦的研究，齿面摩擦力存在影响轮齿啮合的弯曲强度kb、剪切刚度ks和径向压缩刚度分量ka，对其他刚度分量的影响可以忽略。下文根据势能法建立齿面摩擦模型。

在主动轮啮入过程中，摩擦力方向由节点指向齿根，此时弯曲势能Ub、剪切势能Us和径向压缩势能Ua如下表示：

在主动轮啮出过程中，摩擦力方向由节点指向齿顶，而弯曲势能Ub、剪切势能Us和径向压缩势能Ua如下表示：

截面积As和惯性矩Is根据公式(17)和公式(18)计算：

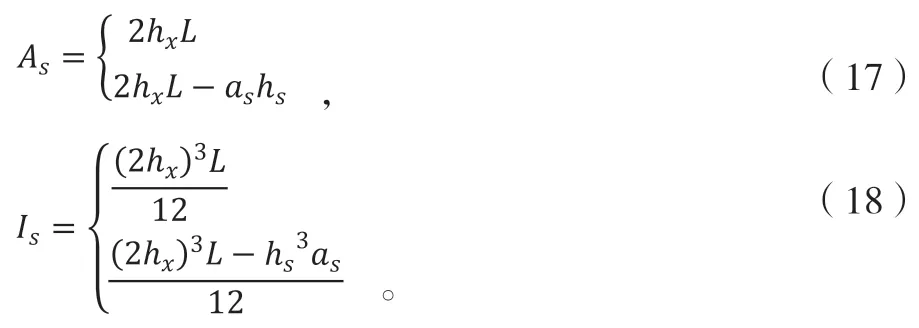
公式(19)、(21)、(23)为剥落故障主动轮啮入时弯曲刚度、剪切刚度和径向压缩刚度计算解析式，公式(20)、(22)和(24)为啮出时弯曲刚度、剪切刚度和径向压缩刚度。同理，可得到考虑摩擦下健康齿轮副的计算模型:

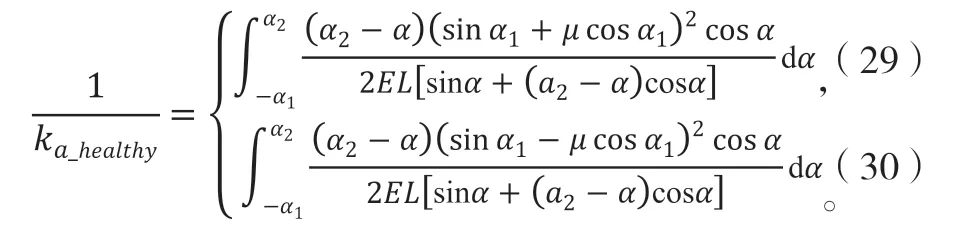
公式(25)、(27)、(29)为啮入时弯曲刚度、剪切刚度和径向压缩刚度，公式(26)、(28)、(30)为啮出时弯曲刚度、剪切刚度和径向压缩刚度。

根据上述所建立的考虑摩擦时齿面点蚀剥落故障齿轮副啮合刚度模型，选取相同的对称剥落故障，同时选取不同定摩擦因数进行计算，所得结果如图11所示。

图11 定摩擦因数下剥落故障齿轮副时变啮合刚度

可以看出，齿面摩擦力对直齿轮副时变啮合刚度影响较大。随着啮合点在节点左右不同，摩擦力方向不同，摩擦力对啮合刚度的影响也会不同。首先齿面摩擦会增大齿轮副双齿啮合区间的啮合刚度，且摩擦因数越大，刚度增加越大；而且在单啮合区间啮入阶段，齿面摩擦会使直齿轮副啮合刚度增大，在单啮合区间啮出阶段，时变啮合刚度减小。因为本模型建立采用的是定摩擦因数，而且摩擦力方向在啮合节点左右改变，导致直齿轮副在单啮合区间节点左右啮合刚度发生突变，突变的幅度随摩擦因数的增大而增大。

2.2 时变摩擦与剥落故障

上文讨论了定摩擦因数下剥落齿轮副的啮合刚度，在直齿轮副啮合传动过程中，其齿面摩擦因数不是定常值，摩擦因数会随着齿轮啮合状态呈现出时变的特点。所以本节展开讨论时变摩擦因数下剥落故障齿轮副的时变啮合刚度。

根据Xu[14]提出的弹性流体润滑理论，直齿轮副齿面摩擦因数会随着齿轮副啮合参数变化，且在齿轮幅啮合节点左右呈现连续变化的趋势，不存在突变，其摩擦因数计算模型如下表示：

根据此模型计算直齿轮副传动过程中齿面时变摩擦因数，齿轮副的润滑特性如表4所示，回归系数如表5所示，可得到齿轮副啮合过程中时变摩擦因数，如图12所示。

表4 齿轮及润滑特性

表5 回归系数

如图12所示，齿面时变摩擦因数随着啮合参数变化，在节点位置处，两啮合轮齿纯滚动，摩擦力为0，当实际啮合点远离节点时，摩擦因数增大，在整个轮齿啮合过程中，摩擦力不发生突变。

图12 时变摩擦因数

利用所得时变摩擦因数，代替2.1节中的定摩擦因数，选取偏心量为3mm的点蚀剥落故障，计算齿轮副时变啮合刚度，所得结果如图13所示。

笔者发现，当利用时变摩擦因数计算时，时变摩擦因数对啮合刚度影响，与定摩擦因数对啮合刚度影响趋势一致，都增大双齿啮合区间和单齿啮合区间啮入阶段的啮合刚度，减小单齿啮合区间啮出阶段齿轮副时变啮合刚度，而且采用连续变化的时变摩擦因数，在单齿啮合区间内，啮合刚度在啮合节点附近的突变消失，呈现出连续变化的趋势。

图13 基于时变摩擦因数下剥落齿轮副啮合刚度

3 结论

为研究渐开线直齿轮副剥落故障和齿面摩擦共同作用时齿轮副时变啮合刚度变化问题，本文建立齿轮齿面剥落和齿面摩擦的模型，推导偏心剥落齿轮副时变啮合刚度计算方程，研究不同剥落偏心量和齿面摩擦对直齿轮副时变啮合刚度的影响。研究表明，当轮齿齿面发生矩形剥落时，会减小直齿轮副时变啮合刚度。

其中，当剥落区域沿着齿轮轴向中心面不对称时，在剥落区域啮合时，发生齿面剥落的轮齿由于齿间受力不均，使轮齿产生扭转变形，相应产生扭转刚度，会进一步减小剥落区域的时变啮合刚度，并随着剥落偏心量增大，扭转刚度减小，齿轮副时变啮合刚度减小。

当齿面摩擦和点蚀剥落故障共同作用于直齿轮副时，定摩擦系数和时变摩擦系数下齿轮副啮合刚度走势相一致，都是增大双齿啮合区间和单齿啮合区间啮入阶段的啮合刚度，减小单齿啮合区间啮出阶段的啮合刚度。在实际工程应用中，应尽量减小齿轮副的制造和安装误差，以及对齿轮副进行良好的润滑，才能尽量保证齿轮副安全运行，延长其使用寿命。