基于外力估计与位置的阻抗控制算法实现

王奇峰 林初畅 贺一民,3 鲍晟,3*

（1常熟国家大学科技园管委会，江苏常熟，215500；2上海大学，上海，200444；3上海机器人研究所，上海，200444）

0 引言

新世纪以来，机器人技术在工业上得到广泛应用。通常在需要与环境有交互的应用场景中，如装配、抛光、打磨等，机器人需要对环境的不确定性有所柔顺，而且要求工具与零件的接触力在一定的工作范围内，因此加入被动柔顺或者主动力控制非常必要[1]。在目前的抛光打磨中，一般采用末端六维力传感器来检测与加工零件之间的接触力信息。不过，在抛光打磨过程中，往往会出现比较大的振动以及热传导，这些会对力传感器的可靠性造成不利影响。因此，无力传感器的力控制方法具有研究意义和应用价值。

很多学者提出了无力传感器获取力信号的方法。Stolt等学者提出了基于关节误差估计外力的方法[2]。Hacksel等学者提出了基于精确动力学和机械臂位置误差估计外力的方法[3]。由于机械臂参数的不确定性，Eom等学者在Hacksel等人的研究成果的基础上加入了自适应的控制策略来克服这些误差[4]。Smith 等学者使用基于神经网络的动力学模型来估计接触力。Colomé等学者将基于任务导向的动力学模型学习与鲁棒扰动状态观测器相结合提出了一种新的外力估计方式。在阻抗控制方面，Chiaverini等学者提出平行力/位控制策略[5]。柳洪义等学者在传统的阻抗控制模型中加入模糊算法来调整参考轨迹，从而提高了机械臂系统对环境的适应性[6]。Mallapragada等学者提出使用人工神经网络来调整控制器的参数[7]。

基于高利明提出的外力估计方法[8]和基于位置的阻抗控制方法，本文提出了一种无需力/力矩传感器的曲面恒力跟踪算法，可以实现末端笛卡尔坐标系下的曲面恒力跟踪，用来模拟曲面的抛光打磨。实验结果表明，该算法非常有效。

1 外力估计

1.1 关节力矩估计

在关节空间中，机械臂的动力学方程为：

本文采用的七自由度机械臂，每个关节均由一个单独的无刷交流电机来驱动，电机的输出力矩可表示为:

机器人关节中所使用的无刷电机通常转速较高，能够提供的力矩相对较小，所以一般需要经过减速机的放大后输出。即:

故方程(1)可写为：

通过综合模型辨识各个机械臂关节的模型参数，并计算模型的拟合误差，如表1所示。其中，代表库伦摩擦，为粘滞摩擦的4个参数，为3个负载扭矩对摩擦力影响的模型中的3个参数。在模型误差评判指标中，RMSE表示均方根误差，MAE表示平均绝对误差，MAPE表示平均绝对百分比误差，RMSPE表示均方根百分比误差。

表1 各关节综合摩擦模型参数

1.2 末端力估计

七自由度机械臂的关节位置和末端位姿满足关系式为：

关节速度和机械臂末端的速度满足：

则机器人关节外力矩和环境施加于机械臂末端外力/力矩的关系可以表示为：

2 力跟踪控制策略

2.1 恒力跟踪建模

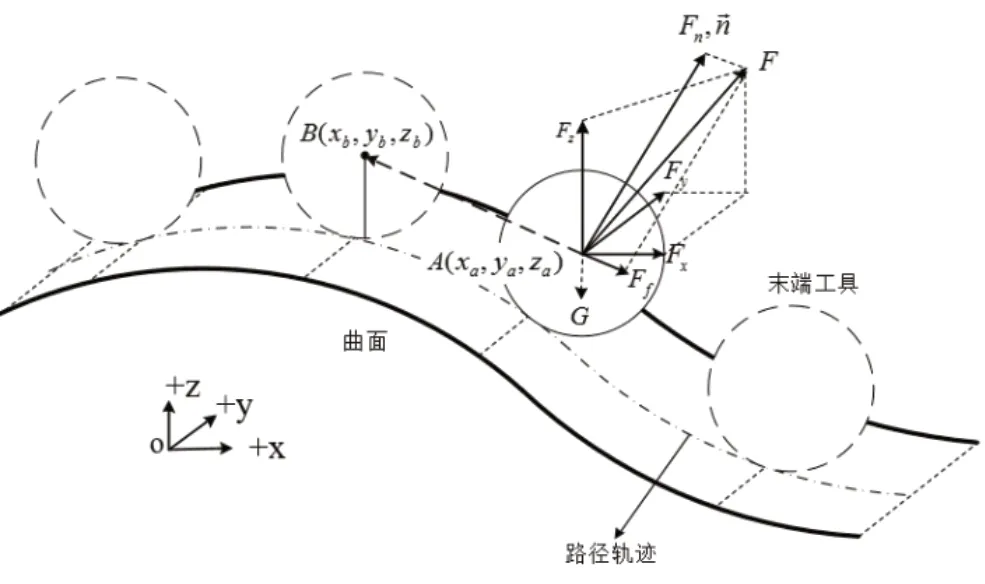
图1 曲面恒力跟踪模型

2.2 基于位置的阻抗控制

阻抗控制将机器人末端和环境的力作用关系等效为一个“质量—阻尼—弹簧”模型，将力控制转化为末端位置的控制。通过调整该模型的质量、阻尼、弹簧刚度3个参数来调整力和位置的效果。在恒力跟踪控制的过程中，机器人表现为阻抗特性，环境表现为导纳特性。

2.2.1 笛卡尔坐标中的动力学方程

一般刚体机器人的动力学方程可以表示为：

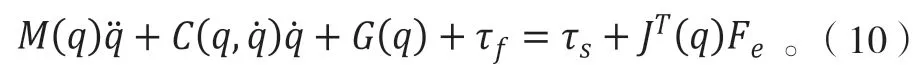
公式（10）是关节空间中的表示形式，而机器人末端的活动是在笛卡尔空间中进行，因此有必要变换为操作空间中的动力学方程。

笛卡尔空间和关节空间变量的基本变换公式：

对方程(11)求导可以得到：

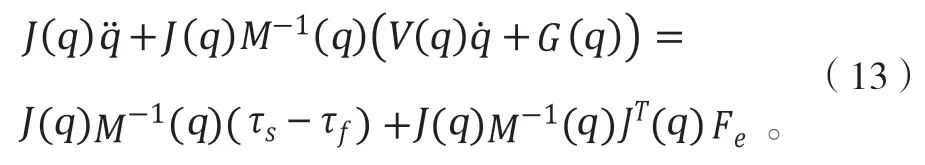
将公式（10）、（11）、（12）带入公式（13）后，两边同时乘以:

方程(14) 为笛卡尔空间中的动力学模型。其中，

公式（10）和（14）本质上可看成是同一个机器人系统的动力学方程，不同的是在关节空间或者笛卡尔空间中描述。这一转化为实现笛卡尔空间的阻抗控制提供了方便。

2.2.2 笛卡尔空间中的期望阻抗模型

根据实现阻抗控制的内环控制方式来分类，阻抗控制可以分为两种：基于位置控制的阻抗控制和基于力矩控制的阻抗控制。对于一般的工业机器人，它的位置控制内环做的非常完善，因此一般选用基于位置控制的阻抗控制。

在阻抗控制中，笛卡尔空间中的期望阻抗模型为：

因此可以得到新的阻抗模型为：

对公式（17）进行拉普拉斯变换可得：

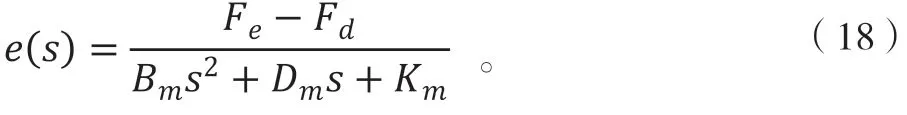
根据上述分析，本文设计了基于位置模式的阻抗控制的恒力跟踪控制原理图（如图2所示）。给定机器人初始位移轨迹 后，机器人开始运动，并且实时测量各关节所受到的外力矩，通过力雅克比矩阵求得末端所受的力。末端受到的实际力和目标力会产生误差值，该误差值经过期望阻抗模型后，输出位移偏差量，该位移偏移量不断去修正初始轨迹位移。当前操作空的间内位置值由机器人根据实时的关节位置信息通过运动学正解计算得到。若当前位置和期望位置不同，便产生一个位移偏差。该偏差量经过位置修正算法反馈给机器人，然后机器人通过逆运动学实时计算目标关节位置值。这里关节目标位置和实际关节位置的差值作为机器人内部位置控制环的输入，确保机器人按期望的运动方式运行。这样就完成了基于位置模式的闭环阻抗力控制。

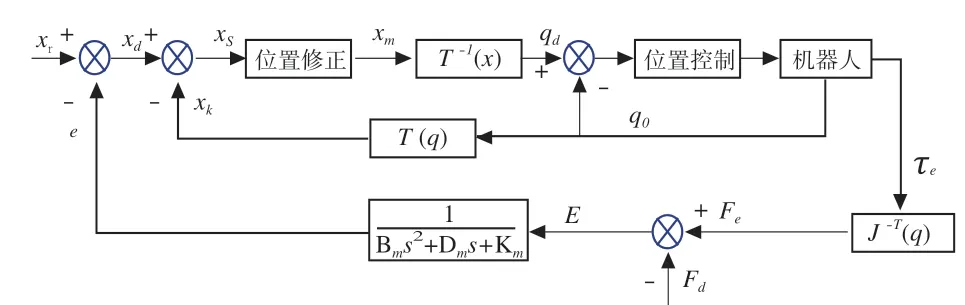
图2 基于位置的阻抗控制框图

对公式（17）离散化处理可得阻抗模型的差分形式：

可以看出，公式（19）包含了相邻的3项位移修正量。若要求出当前的位移修正量, 需要先得到其前周期的值。实际应用中，在初始条件下，通常先设定前周期初始值为0。

3 机器人曲面恒力跟踪动态轨迹规划

3.1 初始轨迹

通过离线获取曲面轨迹方程的方式来确定初始化轨迹。该轨迹方程的坐标是机器人的基座坐标，也是固定坐标系。机器人末端的位置也是相对于该固定坐标系，机器人末端的姿态是相对于该固定坐标系的 PRY 旋转。

3.2 轨迹动态调整

在末端工具沿着曲面运动过程中，利用微分法的思想，将运动轨迹分割成无数个极小的步长，每一个极小步长内的运动可以认为是直线运动。在实际应用中，极小步长就是机器人控制系统一个周期内末端的行进步长。本文以控制周期为 4ms，按照末端10mm/s的速度来计算，一个步长的距离是0.04mm，相对于一般的曲面尺寸来说，可以认为步长是足够小的。

本文的目标是保证沿着曲面法向方向保持恒力，则问题转化为已知A 点的当前位置信息和受力情况，计算出下一点的位移修正量。

然后，根据上文中的外力估计得到的末端力信号计算出末端与曲面的实际接触力，控制系统可以实时计算出A点的受力,其模值为。

由此得到A点的法向接触力为 在法向矢量上的分量：

4 实验分析

本实验采用的机械臂为协作机械臂，如图3所示。各关节坐标系采用改进DH法建立，具体DH参数如表2所示。其中 为连杆编号；为连杆扭转角；为连杆长度；为连杆偏距；为关节角度。

图3 七自由度机械臂

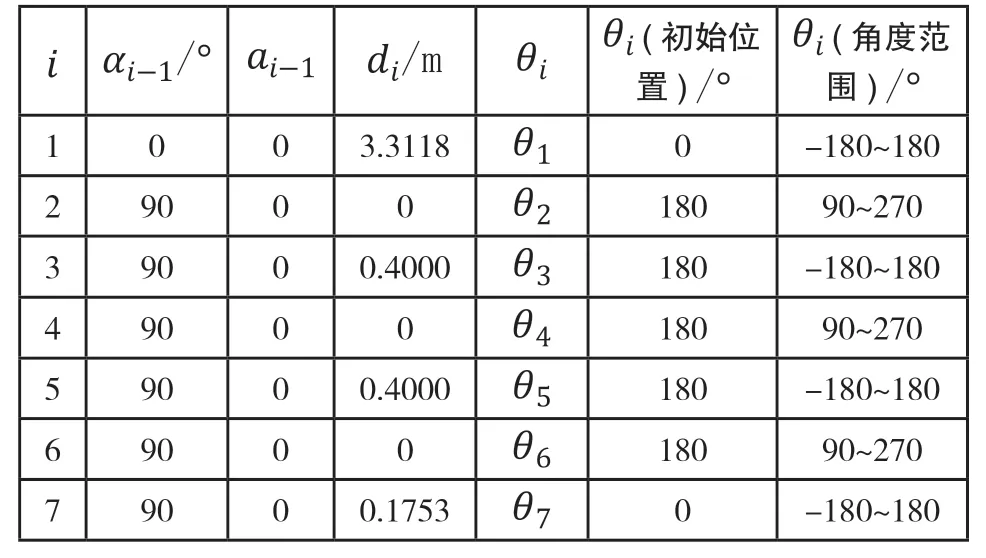
表2 机械臂改进DH参数表

笔者利用本文设计的曲面恒力跟踪控制算法来跟踪一个给定的正弦曲面，实验装置如图4所示。经过不断调试，实验参数设置见表3。

图4 实验装置

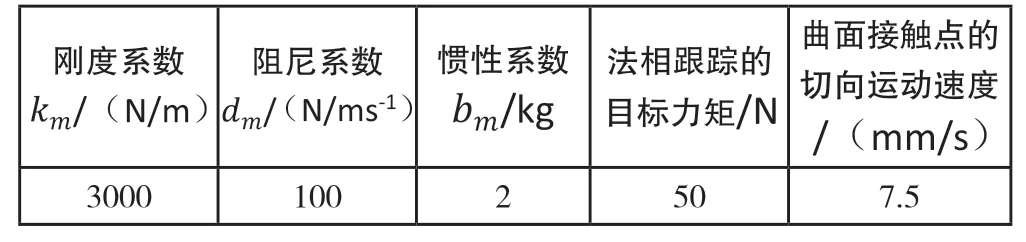
表3 实验参数设置

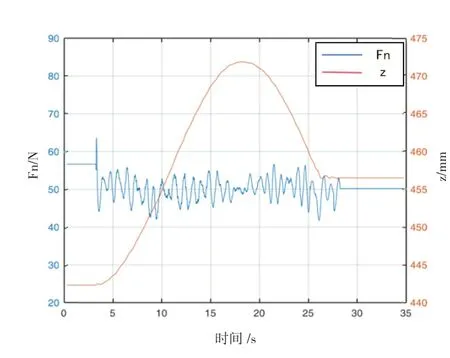
图5 期望力为50N的曲面轮廓和法向力

图6 接触力z向分量

在给定的参数条件下，机器人可以按照预定轨迹和法向作用力沿着曲面平稳运行，各项指标均达到预期效果，成功实现了无力传感器的曲面恒力跟踪控制实验。实验结果如图5所示，其中，红色曲线表示曲面z方向的数值，蓝色曲线表示在跟踪过程中的法向接触力值Fn。可以看出在机器人末端工具的整个运动过程中，虽然位置在不断发生变化，但是法向力却能够在期望力附近保持恒定，跟踪误差在±8N之内。

图6所示为接触力 z 方向的分量变化情况，图7为接触力在 x 方向的分量变化情况，图中红色曲线代表利用关节电流值和动力学模型估计得到的力信号值，而绿色曲线表示利用末端的力传感器实时测量得到的力信号。其中 x 方向的分量随着末端工具的位置变化而有明显变化，这也符合实际。另外可以看出，电流估计值和实测值的差值误差在可接受的范围内，因此该实验表明外力估计算法是比较精确的，达到了期望目标。

5 结论

本文使用一种无力传感器的外力估计方案，通过获取关节电机的电流来计算输入力矩，根据机器人精确的动力学模型计算出无外力情况下的理论关节力矩，即实际输入力矩和理论力矩的差值，在得到关节外力矩值后，左乘力雅克比矩阵，即可求得作用于机器人末端的外力。在此基础上，本文根据基于位置控制模式的阻抗控制理论，设计了一种恒力跟踪曲面的力控制算法，可以控制机械臂末端执行器与目标曲面在接触运动的同时，使某个方向的接触力保持恒定。实验证明，本文提出的方法可以精确地对外力进行估计，而且可以控制机械臂末端工具平稳地跟随给定的曲面，跟随力的精度达到了预期目标。