混沌反馈共享和群体协同效应的蝴蝶优化算法

李守玉，何 庆＋，杜逆索

1.贵州大学大数据与信息工程学院，贵阳550025

2.贵州大学贵州省大数据产业发展应用研究院，贵阳550025

为了更好解决现实中的复杂优化问题，研究者们通过观察、研究自然界中生物的生理或物理现象，提出了粒子群优化算法、灰狼优化算法、樽海鞘优化算法、飞蛾扑火算法及蝴蝶优化算法等元启发式算法，并将它们用于解决现实中的工程优化任务。

传统的粒子群算法虽收敛速度快、易于实现，但存在早熟现象，蚁群算法虽有较强的记忆性，但它容易出现停滞现象且效率低。蝴蝶优化算法（butterfly optimization algorithm，BOA）是由Arora和Singh 于2019 年提出的基于全局优化的群智能算法。BOA通过蝴蝶之间散发的香味形成一个具有一定信息损失的一般社会交互网络，其具有原理简单、参数少、计算耗时少及易于实现等优点，因此被应用于阴影光伏阵列的重构技能的工程设计、优化无线传感器网络的能量有效簇、小波神经网络的训练、家庭CO减排策略混合智能预测模型及认知智能电网中基于能效优化的频谱分配策略等领域。

然而蝴蝶优化算法也存在收敛速度慢及寻优精度不高的缺陷。为此，研究者提出了不同的改进策略。文献[9]通过将柯西变异和自适应权重结合增强算法跳出局部最优的能力和全局搜索的能力，使用动态切换概率调节全局与局部搜索的比重。文献[10]利用混沌理论与正余弦算法结合的方式增强算法的寻优能力，使用线性递减控制香味的幂指数提高收敛精度。文献[11]通过交叉熵和协同进化技术找寻全局与局部搜索之间平衡，提高算法的全局搜索能力。文献[12]利用limit 阈值克服陷入局部的难题，再将单纯形法和正弦余弦指引策略结合对位置进行更新，提高算法的寻优性能。文献[13]利用扰动策略和疯狂因子增加算法的多样性，通过线性递减惯性权重平衡全局与局部搜索的能力。尽管改进算法寻优精度有所提升，但收敛速度和稳定性仍有很大改进空间。

针对蝴蝶优化算法存在的问题，本文提出了混沌反馈共享和群体协同效应的蝴蝶优化算法（butterfly optimization algorithm based on chaotic feedback sharing and group synergy，CFSBOA）。算法利用二维的Hénon映射，使得种群个体的搜索分布更加均匀，增加算法多样性；通过正反馈或负反馈网络加快算法的信息流动，进而增强逃离局部最优的能力；最后融合群体协同，进一步矫正和协调种群的进化方向及更好地平衡全局与局部搜索能力。通过求解12个基准测试函数和部分CEC2014测试函数验证算法的有效性和鲁棒性。

1 蝴蝶优化算法

在标准BOA 算法中，蝴蝶种群采用随机初始化蝴蝶种群：

式中，表示蝴蝶种群规模，表示搜索空间维度。

蝴蝶算法假定搜索空间中的每个个体能感知彼此散发的香味；蝴蝶能根据香味浓度的强弱进行随机移动或向最好蝴蝶移动；蝴蝶的感觉模态受目标函数的范围影响或决定。由于蝴蝶进行食物源搜索时，香味大小受风、雨、温度等因素影响和限制，采用转换概率控制蝴蝶的搜索模式：全局搜索或局部搜索。

蝴蝶香味计算公式：

其中，代表香味大小；是感官模态强度；是刺激强度；是依赖感官模态的幂指数；表示最大迭代次数。

蝴蝶的位置更新由局部搜索和全局搜索构成。若蝴蝶因距离和自然因素无法感知到其他蝴蝶散发的香味，则蝴蝶在局部执行随机搜索；若蝴蝶能够感知到其他蝴蝶散发的香味，它能根据香味强弱，飞向最好蝴蝶实现蝴蝶位置更新，从而使得种群向食物源位置进行搜索。

当≥时，进行局部搜索：

当＜时，进行全局搜索：

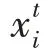
2 混沌共享反馈和群体协同效应的蝴蝶优化算法

2.1 Hénon初始化机制

标准BOA利用式（1）随机初始化蝴蝶位置，可能会出现蝴蝶位置在搜索空间中分布不均匀，导致算法过早陷入局部最优，出现早熟现象。文献[14]利用Tent映射初始化樽海鞘种群，使得樽海鞘个体均匀分布在搜索空间上，从而提高算法寻优精度。

混沌映射具有遍历性、随机性和规律性等优点，其基本思想利用映射关系产生[0,1]的混沌序列，再将混沌序列转化到个体的搜索空间。常用来初始化种群的混沌映射有Tent映射、Logistic映射，但文献[15]指出Tent 映射存在小周期和不稳定周期容易使Tent映射易陷入不动点；Logistic 映射在[0,1]范围内呈切比雪夫分布，搜索盲区大。然而Hénon 不仅能克服Tent映射和Logistic映射的缺点，其产生的混度序列也更加均匀，如图1所示。利用Hénon的混沌序列分布更加均匀的特点，种群可以最大程度覆盖搜索盲区，增加蝴蝶个体的多样性，从一定程度上帮助算法跳出局部极值，进而增强算法寻优的能力。因此，本文采用Hénon混沌映射初始化蝴蝶种群。其数学描述：

图1 Hénon混沌映射Fig. 1 Hénon chaotic mapping

2.2 反馈共享机制

由于标准BOA算法只通过全局最优解的位置进行信息交流，很大程度上限制蝴蝶的搜索范围，增大算法陷入局部最优的风险，降低算法的寻优精度。为了增强算法跳出局部最优的能力，参考电路分析中反馈控制电路的概念，让蝴蝶受到其他蝴蝶的正反馈或负反馈的作用。具体表现受生物互惠互利的行为机制影响，让蝴蝶受到比自身适应度好的个体的正反馈作用以及比自身适应度差的负反馈作用，从而使得蝴蝶能够感知到更多方向的位置信息，增强蝴蝶的全局搜索能力。

从搜索空间中随机选择一只蝴蝶，与当前蝴蝶、最优蝴蝶构建香味反馈机制实现信息共享。在飞行过程中，蝴蝶散发的香味会向不同方向传播，为搜索空间中其他蝴蝶寻优提供有利信息。因此，假设每只蝴蝶能向两个不同方向传播香味，然后决定它将飞向哪个方向，两个传播方向分别是随机蝴蝶所在方向和最优蝴蝶所在方向。通过香味反馈机制，当前蝴蝶根据传递的香味信息能够知道食物是否在这两只蝴蝶周围。若随机蝴蝶的适应度比当前的蝴蝶的适应度更好，则认为该食物存在，否则附近没有食物来源。

如果食物源被证实存在于两只蝴蝶的周围，通过正反馈作用，当前蝴蝶会移动到两只蝴蝶周围。如果不是，通过负反馈作用，它向最好的蝴蝶移动。数学模型描述如下：

香味反馈机制使得蝴蝶个体可以更多地围绕最佳位置进行挖掘，同时式（13）提出的飞行方向使蝴蝶个体运动方向具有多样性化的能力，可以增强探索能力，特别是在迭代的初始阶段，可以避免过早收敛。

2.3 群体协同效应位置更新机制

标准BOA中计算蝴蝶之间距离计算方式存在如下缺陷：（1）更新后的蝴蝶个体对前一次迭代的蝴蝶会产生很强的依赖性，具有一定盲目性致使算法出现停滞，从而导致收敛速度下降。（2）算法全局搜索和局部开发的能力受到很大限制，这也是标准BOA算法寻优精度不高的主要原因。为了进一步提升和平衡标准BOA 算法的全局搜索和局部搜索能力，受文献[16]和文献[17]共同启发，本文将黄金正弦算法作为媒介，提出群体效应位置更新机制，针对式（5）、式（6），进行如下改进。

其一，利用黄金分割数不需要梯度信息的优点，对标准BOA算法的距离公式进行改进；其二，群体协同效应主要由个体矫正因子和群体协调因子构成，其利用正弦曲线值域分布特点，具体如下：

新局部搜索公式：

新全局搜索公式：

综上三节，利用混沌初始化种群，使得种群分布更加均匀，为后续算法寻优打下基础。通过反馈共享，引入随机蝴蝶加快蝴蝶种群之间的信息交流实现信息流动达到共享，增强算法跳出局部最优能力。引入群体协同，降低蝴蝶的盲目依赖性，增强及平衡全局和局部搜索能力。寻优过程中，蝴蝶种群能够进行针对性的搜索，调整适合个体进化方向，进而增强算法寻优能力。

2.4 改进算法的步骤

CFSBOA算法：

2.5 时间复杂度分析

CFSBOA算法主要由混沌初始化、反馈共享及群体协同效应组成，假设种群规模为，搜索空间维度为，则BOA的随机初始化的时间复杂度为(×)，计算个体适应度为()，迭代过程中的时间复杂度为(×)，更新最优解的时间复杂度为(1)，BOA总的时间复杂度为(×)。

同理，CFSBOA 在BOA 的基础上将随机初始化替换为混沌初始化时间复杂度为(×)，增加的反馈共享机制的时间复杂度为(×)，增加的群体协同机制的时间复杂度为(×)，因此CFSBOA总的时间复杂度为(×)。因为CFSBOA和BOA的时间复杂度一样，所以CFSBOA并未对算法产生负面影响。

3 实验仿真与结果分析

实验环境为Windows 7，64 位操作系统，CPU 为Intel Core i5-6500H，主频3.2 GHz，内存8 GB，算法基于MATLAB2014b编写。

为了充分验证本文所提出的CFSBOA在求解复杂优化问题时的鲁棒性和有效性，将CFSBOA 算法与加入混沌初始化的蝴蝶算法（chaotic butterfly optimization algorithm，CBOA）、加入反馈共享机制的蝴蝶算法（feedback butterfly optimization algorithm，FBOA）、加入群体协同效应的蝴蝶算法（sharing butterfly optimization algorithm，SBOA）、BOA、MFO（mothflame optimization）、SSA（salp swarm algorithm）和GWO（grey wolf optimize）在12个经典测试函数上进行最优值求解，然后进行实验对比。

采用如表1 所示的12 个基准测试函数作为目标函数，测试函数包含单峰可分（unimodal sepa-rable，US）、单峰不可分（unimodal non-separable，UN）、多峰可分（multimodal separable，MS）、多峰不可分（multimodal non-separable，MN）等不同特征的函数。同时，测试函数的维度跨度大，从2维到200维，因此可以更加全面地检验算法的综合性能。

表1 基准测试函数Table 1 Benchmark functions

为保证每种算法对比的公平性，实验中最大迭代次数设为500，种群规模为30，独立运行50 次，其余参数设置如表2所示。

表2 主要参数Table 2 Main parameters

表3 通过最优值、平均值、标准差、成功率（success rate，SR）以及平均耗时（单位：s）五个性能指标来评估各算法的性能，实验对比数据如表3所示。其中，成功率是计算成功次数与实验的总次数之比，一次求解成功率公式如下：

表3 基准测试函数结果对比Table 3 Results comparison of benchmark test functions

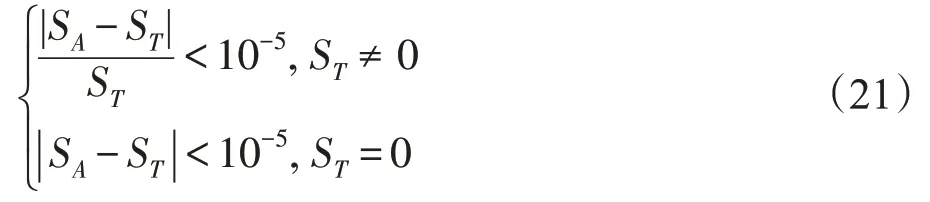
式中，S为每次求解的最优值，S为基准测试函数的最佳值。

首先，表3通过最优值和平均值来反映算法的寻优精度和收敛速度的能力。对于5个单峰函数～，CFSBOA对、和函数求解时，找到了理论最佳值。随着函数维度增加，算法求解最优值的难度也将呈指数增长，因此在和函数上寻优精度有所降低，并未寻到理论最佳值。伴随着函数维度的增加，对比算法MFO、SSA 和GWO 的精度有所下降，尤其是在求解50 维的时，MFO 与理论最佳值相差1.0×10的量级。对于CBOA、FBOA 和SBOA 的寻优精度和收敛速度，三种改进策略得到的结果均比BOA 好，这充分证明了不同改进策略对算法的寻优能力均有不同程度的增强。在5个单峰函数上，除上CFSBOA 的平均值略微高于SBOA 外，CFSBOA的综合性能均比其他几种算法好。对于7 个多峰函数～，与单峰函数相比，多峰函数的求解会变得更加困难，因此寻优精度低于单峰函数。随着多峰函数维度增加，CFSBOA在对7个多峰函数求解时，5个多峰函数上能寻到理论最佳值。对7 个多峰函数寻优时，CFSBOA、SBOA 和FBOA 算法的寻优能力均优于标准的BOA，CBOA仅在的寻优能力不如BOA，但在其他函数的寻优能力均强于标准BOA。在上，CFSBOA、SBOA 和FBOA 的寻优精度和收敛速度都比其他算法要好。在上，各算法都找到理论最佳值，但CFSBOA 的平均值和标准差均比其他算法好。其余函数的求解上，CFSBOA 都能寻到理论最佳值，进一步验证了三种改进策略的寻优有效性。由此可见，CFSBOA 对单峰可分、单峰不可分、多峰可分和多峰不可分及高维度的基准测试函数有着明显的优势。

其次，表3中成功率和标准差体现算法跳出局部最优的能力及稳定性。CFSBOA 的结果很接近理论最佳值，标准差也比较小，对基准测试函数寻优有着较强的稳定性。在12 个基准测试函数上，CFSBOA的寻优成功率都是100%，SBOA 在11 个函数寻优成功率为100%，FBOA在9个函数成功率为100%，虽然CBOA在～的成功率不如标准BOA，但其在8个函数上寻优成功率为100%，而标准BOA只在7个函数上成功率为100%。另外，随着基准测试函数维度增加，标准BOA的寻优精度不高的特点愈发明显，精度大多停留在10以下，而CFSBOA 和FBOA 引入的反馈共享机制，增加算法逃离局部最优能力，寻优精度得到提高；CFSBOA和SBOA引入群体协同效应使得算法的寻优精度和收敛速度大幅提升，证明了反馈共享机制和群体协同效应机制对算法的局部和全局搜索能力有很大的增强作用。

最后，从平均耗时角度分析。由表3 可知，MFO和SSA 的平均耗时最短，改进算法相对标准BOA 平均耗时都要长，因为改进策略中引入更多的机制使得算法不仅能在搜索空间中进行大范围搜索，还能找到更多的解，所以导致算法平均耗时变长，但是CFSBOA 的平均耗时与其他算法相比，所增加部分在可接受范围内。

为了形象地观测改进策略的性能，对CFSBOA与SBOA、FBOA、CBOA、BOA、MFO、SSA 与GWO进行收敛性分析。图2 给出部分测试函数的平均收敛曲线图。因为寻优精度较高，为了便于观察平均曲线的收敛情况，本文的纵坐标取以10为底的对数。

在单峰函数上，CFSBOA 的寻优精度最高，SBOA 其次，其余算法的寻优精度都不高，同时CFSBOA 的收敛速度最快。在上，寻优精度依次为CFSBOA、SBOA 和FBOA，其余算法的精度不高，CFSBOA 相比其他算法求解最佳值的迭代次数更少并且能够快速收敛。

在多峰函数上，所有算法未能寻到最佳值，但CFSBOA、SBOA 和FBOA 的寻优性能突出，寻优精度比其他算法高，CFSBOA和SBOA能够快速收敛到精度较高的解上且收敛速度较快。在上，所有算法都寻到最佳值，但CFSBOA 和CBOA 收敛速度最快，CBOA对于该函数的寻优能力相比其他函数优势突出。在上，CFSBOA虽未能寻到最佳值，但寻优精度最高且相比其他算法收敛速度快。在上，CFSBOA 和FBOA 都能寻到最优值；对于收敛速度，CFSBOA 收敛速度最快，FBOA 其次，SBOA 慢于两者，其余算法收敛速度慢且收敛精度低。

另外，由图2（a）～（f）可以看出，在种群迭代前期，CFSBOA、SBOA 和FBOA 曲线速度下降很快且寻优精度很高，说明引入群体协同机制和反馈共享机制能够增强算法跳出局部最优的能力，使得算法在迭代开始时收敛速度变快。随着迭代的进行，CFSBOA能够持续寻优，而其他算法在迭代后期陷入局部最优出现停滞状态。同时，在上，CFSBOA比只增加反馈共享机制的FBOA 收敛速度更快且寻优精度更高，证明了群体协同效应机制，通过对个体和群体的协同配合使得种群逃离局部最优和全局搜索的能力得到增强，有利于算法的持续寻优。在上，CFSBOA 比只增加群体协同效应的SBOA收敛速度更快，这证明反馈共享机制能帮助算法快速找到最优解位置附近。另外，CFSBOA在和上寻到了基准测试函数的理论最佳值。除了在上，FBOA 的平均收敛曲线和标准BOA 平均收敛曲线在一个数量级上，其余改进算法的平均曲线都在标准BOA算法平均收敛曲线的下方，验证了改进算法的有效性。结合表3 和图2的实验结果和平均收敛曲线图证明，不管基准测试函数是单峰、多峰，还是在低维、高维，CFSBOA的综合性能均比其他算法要好。图2（b）和图2（f），因纵坐标取对数的原因加上CFSBOA在这两个函数上找到了0，所以曲线后面没有显示。

图2 基准测试函数平均收敛曲线Fig. 2 Average convergence curve of benchmark test functions

根据Derrac等人在文献[21]中提出的，对于改进进化算法性能的评估，需要进行统计检验。本文选择用Wilcoxon 秩和检验并在5%的显著性水平下进行。表4 给出了CFSBOA 和其他算法在所有基准测试函数上的值。假设CFSBOA 为最佳算法，则在CFSBOA vs SBOA、CFSBOA vs FBOA等之间进行成对比较。另外，由于最佳算法与自身无法进行比较，因此针对最佳算法采用N/A标记，代表“不适用”，符号“=”“+”和“-”分别代表相当于、优于、劣于对比算法。Derrac 等人的文献中指出值小于0.05 认为是拒绝零假设的有力验证。表4结果表明，CFSBOA的值基本小于0.05。只有在、的CFSBOA vs CBOA时，值大于0.05。这表明CFSBOA算法的优越性在统计检验上是显著的。因此可以认为CFSBOA算法比其他算法具有更高的收敛精度，值大于0.05已用粗体显示。

表4 基准函数Wilcoxon秩和检验的p 值Table 4 p value for Wilcoxon's rank-sum test on benchmark functions

文献[22]提出使用平均绝对误差（mean absolute error，MAE）对优化算法进行排序，这是一种有效且可行的性能指标。表5 中所有算法的分析是基于12个基准测试函数的MAE。MAE公式如下：

表5 各算法MAE排名Table 5 MAE ranking of each algorithm

式（22）中，B为算法最优值的平均值；V为相应基准函数的理论最优值；N为基准函数个数。

由表5 可知，CFSBOA 排名第一，CBOA 排名第二，SBOA 排名第三。同时，与另外七种算法相比，CFSBOA的MAE值最小。表5的实验数据进一步表明了CFSBOA算法的有效性和鲁棒性。

为了更进一步评估CFSBOA 的有效性和鲁棒性。实验2 分为两个环节：第一环节主要采用CEC2014 函数对CFSBOA 的综合性能进行验证；第二环节验证CFSBOA的竞争性，在保证种群规模、迭代次数、独立运行次数及基准测试函数维度相同的条件下，将其与目前改进蝴蝶优化算法及新改进的群智能算法进行公平对比。

本文在CEC2014测试函数选取部分单峰、多峰、混合(hybrid function，HF)及复合(composition function，CF)函数类型进行验证，所选CEC2014部分函数如表6所示。为了保证算法对比公平性，将种群规模设为30，CEC2014函数的搜索维度设为30，迭代次数500，独立运行30次，实验结果如表7所示。

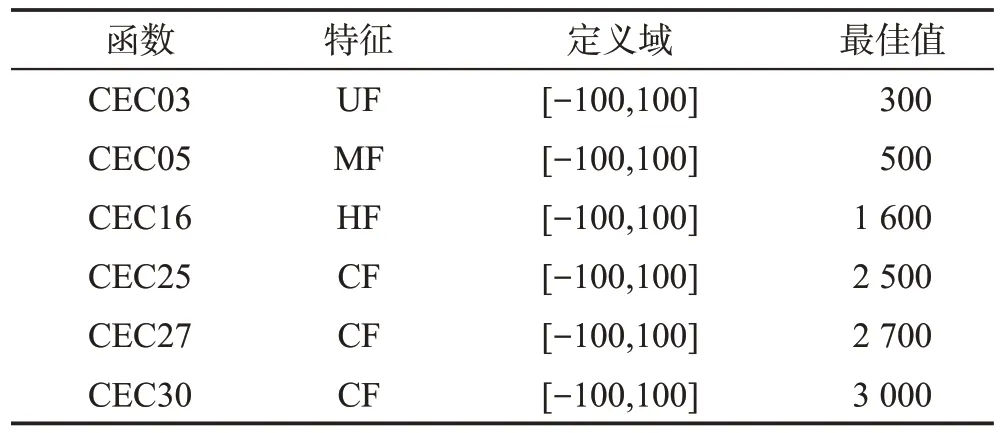
表6 CEC2014函数（部分）Table 6 CEC2014 function(part)

表7 分别记录各种算法的平均值和标准差，因CEC2014函数较为复杂，很难找到最佳值。由表7可知，CFSBOA 在CEC03 的平均收敛不如GWO 和PSO，但标准差远低于两者；在CEC05和CEC16函数的平均值略低于GWO、MFO、SSA 和PSO，但CFSBOA的标准差低于四种算法。另外在最后三个函数上，CFSBOA 算法的平均值和标准差均低于其他算法，验证CFSBOA算法的鲁棒性和有效性。

表7 CEC2014测试函数的结果对比Table 7 Comparison of CEC2014 test function results

与参考文献中数据进行对比，每个算法的种群规模设为30，迭代次数为500，基准测试函数搜索维度为30，对独立运行30 次后的结果进行对比，其中“—”代表无数据，如表8所示。

由表8可知，CFSBOA算法在、、、、和函数上平均值均为最佳值；在和函数平均值高于MSIWOA（multi-strategy improved whale optimization algorithm）算法和CWBOA（Cauchy variation and adaptive weight butterfly optimization algorithm）算法；在上，CFSBOA算法寻优性能不如MSIWOA算法；在上，CFSBOA的标准差高于MPA（marine predator algorithm），而在其余函数上CFSBOA算法的平均值和标准差低于其他算法。因此，本文提出的CFSBOA算法在求解复杂优化问题上具有一定的竞争性。

表8 与参考文献中算法平均值和标准差的结果对比Table 8 Results comparison of mean and standard deviation of algorithms in references

综上所述，实验1 和实验2 的实验结果充分证明了混沌反馈共享和群体协同效应的蝴蝶优化算法对于求解多种类型的基准测试函数，尤其是多峰、高维的函数具有较好的鲁棒性和较高的寻优精度。

4 结束语

为了增强标准BOA算法的跳出局部最优的能力及提高算法的寻优精度和加快收敛速度，本文提出了混沌反馈共享和群体协同效应的蝴蝶优化算法，并将改进的蝴蝶优化算法应用于基准测试函数和CEC2014 函数寻优。混沌机制对种群进行初始化，增加种群的多样性，该机制对特定函数优势明显；迭代过程中，通过利用正负反馈的原理，构建反馈共享网络使得蝴蝶信息来源更加多元，增强算法逃离局部最优的能力；利用群体协同效应平衡和增强算法的全局和局部搜索能力，提高寻优精度和加快算法收敛。三个改进机制能增强算法跳出局部最优的能力，同时提高寻优精度和加快算法收敛能力。另外，本文不仅使用最优值、标准差等指标对算法评估，还使用统计检验Wilcoxon 对算法进行显著性分析和MAE 排序各算法，实验结果表明CFSBOA 算法具备出色优化性能，全局和局部搜索能力得到增强，能够收敛到精度更高的最优解，同时算法的有效性和鲁棒性也得到验证。

在未来，准备改进混沌机制增强其对测试函数的一般性以及将改进的蝴蝶优化算法应用于实际的工程优化问题，解决工程问题的同时，进一步验证算法的性能。