时空轨迹和复合收益的动态上车点推荐

郭羽含，刘秋月

辽宁工程技术大学 软件学院，辽宁 葫芦岛125105

随着移动互联网技术的快速发展，网约车已成为人们出行的重要手段。在乘客与司机匹配后，司机需前往固定位置接驾乘客，而该位置的选择不但影响司机的接驾效率，也对乘客的等待时间、乘客的安全性以及周边的交通拥堵情况具有显著影响。因此，上车点的推荐方法具有重要的研究意义。

目前国内外对于网约车的研究主要集中在时空热度与路径规划等方面，推荐最佳上车点的研究较少。现存研究主要采用两种推荐方法：（1）基于潜在上车点与乘客出发地的距离，如贺明慧将问题抽象为“二分类问题”和“排序问题”进行建模并通过聚类算法挖掘出潜在上车点，之后以乘客到上车点的步行距离及司机到上车点的接驾距离作为主要衡量标准筛选出最适合乘客的上车点；钟颖通过司机与乘客当前位置信息，获取在预设步行距离阈值范围内所有候选上车点，根据设定的步行距离和乘客期待上车点的位置，及司机接驾路程和司机期待到达上车点时长，确定乘客与司机可接受范围内的上车点，为乘客推荐最佳上车点。对于上车点的路网匹配问题，马云飞采用点到线匹配算法，通过计算待匹配点的运动方向与各路段行驶方向的夹角，定义匹配函数，将待匹配点匹配到匹配度最高的路段。（2）基于潜在上车点的拥堵程度，如张旭东对于多个潜在上车点通过其订单量计算该上车点的拥堵权重，将拥堵权重最小的上车点推荐给乘客；张岩通过筛选预设范围内的多个候选上车点，统计各上车点所处路段当前的路况信息，并根据历史订单数据预测未来时间的路况信息，为乘客推荐综合路况最好的上车点作为最佳上车点；张海强获取在预设范围内所有满足条件的候选上车点，根据各候选上车点路况信息及司乘双方各自前往上车点的交通方式，计算司机与乘客完成上车事件的总时间并进行升序排列，选取耗时最少的上车点作为优先推荐给乘客的最佳上车点。

现存方法仍未能较好地解决以下挑战：（1）以聚类或理论计算得出的潜在上车点无法保证其可达性，即司机或无法通过道路抵达该位置；（2）基于单一指标推荐的上车点往往在其他指标上存在显著弊端，未在司机收益和乘客便利性之间取得较好平衡，导致司机与乘客需进行后续沟通调整，从而降低了服务和出行效率；（3）上车点的安全性是目前网约车平台亟待解决的问题，因此需将上车点在不同时段的安全性纳入推荐的考量范围；（4）如何避免由于同时段同上车点推荐量增加所造成的交通拥堵，即实现上车点合理有效分配，减少资源浪费。

针对上述挑战，本文通过对时空轨迹大数据进行归纳与分析，提取保证可达性的潜在上车点，构建最佳上车点的动态推荐模型。将乘客步行收益、司机驾驶收益、上车点路况指标、周边安全性等关键因素纳入衡量标准，并以约束控制同时段同点的推荐量，有效解决同时段由于单点订单堆积而造成的非必要等待和资源浪费。实验表明本文模型和推荐方法可实现上车点的有效动态分配，提升全局司机接驾效率并降低乘客等待时间，且推荐结果优于现存方法。

本文的贡献主要包含以下三点：

（1）提出了一种基于时空轨迹数据的潜在可达上车点提取方法；

（2）形式化定义了多维度收益指标，并提出了一种复合收益评价模型及一种基于高差值优先的动态推荐方法；

（3）基于真实网约车数据，对不同推荐策略进行了比较，并分析了其对收益的影响。

1 问题描述与建模

1.1 基本定义

（上车点）对于给定点集={h，h=＜,,,＞表示1 个潜在上车点，为点标识，∈N 且≤，为上车点集的上车点数，表示上车点的采集时间，和表示上车点的经度和纬度，表示上车点当前被分配人数。

（乘客）乘客集={r}表示当前所有乘客集合，r=＜,,,,,＞表示1 位乘客个体，为乘客标识，∈N 且≤，为乘客集的乘客数，表示乘客叫车时间，和表示乘客叫车位置的经度和纬度，和表示乘客目的地位置的经度和纬度。

（司机）司机集={d}表示当前所有车主集合，d=＜,,＞表示乘客r所对应的司机标识，为车主标识，∈N 且≤，为司机集的车主数，和表示司机当前所在位置的经度和纬度。

1.2 数学模型

式中，∂、分别为L、L的权重。

（上车点安全指标） P为=的上车点处安全性指标。本文对有监控的位置进行标注，并将其监控范围进行经纬度标注，从而将上车点是否处于监控范围内作为乘客上车安全性指标P的判别标准，1 表示该乘车点处于监控覆盖范围内，否则为0，即：

进而，本问题的目标函数可定义为：

研究所涉及的参数及变量见表1。

表1 参数及变量Table 1 Parameters and variables

2 求解算法

对于本文提出的动态上车点推荐模型，包括潜在上车点提取、时空轨迹点匹配、同时段同点推荐量约束及高差值优先算法生成乘客推荐次序等具体步骤，其算法架构如图1所示。

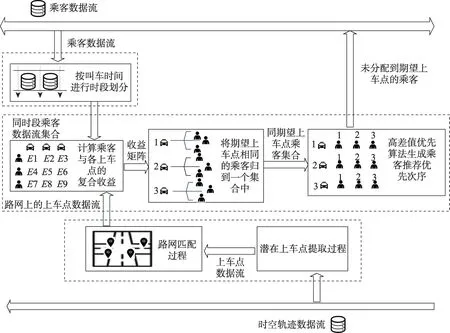
图1 算法架构图Fig. 1 Algorithm architecture

2.1 潜在上车点提取

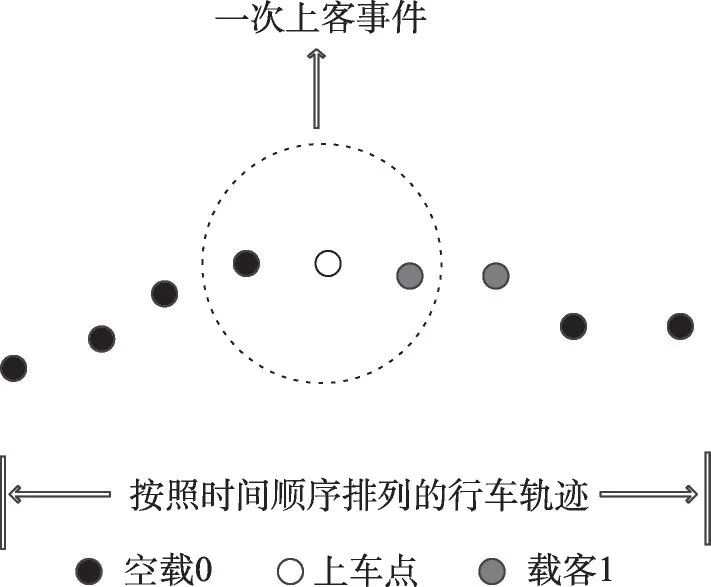
图2 载客事件图Fig. 2 Passenger incident diagram

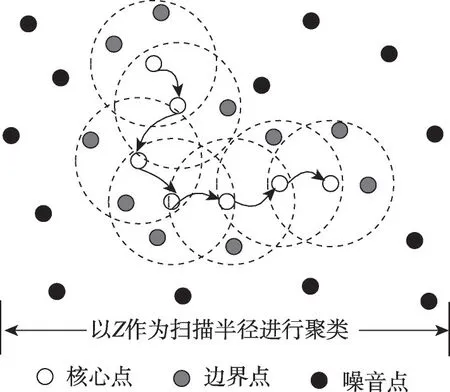
图3 DBSCAN算法示意图Fig. 3 Schematic diagram of DBSCAN algorithm

2.2 时空轨迹点匹配

采用点到线匹配算法将潜在上车点与路网上的路段进行匹配。算法以误差阈值为半径，以待匹配点为圆心进行搜索，获得误差范围内的候选点集合与待匹配路段集合。计算待匹配点运动角度与候选路段行驶方向的夹角，从而定义匹配度函数如下：

其中，λ和λ为权重；为待匹配点运动角度与路段行驶方向夹角的倒数；为待匹配点到候选路段的垂直距离。如图4 所示，以待匹配点为圆心，误差为半径搜索到的候选点集为{1,2,3,5,6,7,8}，待匹配路段集为{,,,}，由点分别向、、、作垂线，依据点的运动角度与各路段的行驶方向，计算各路段的匹配度，将点归于匹配度最高的路段。

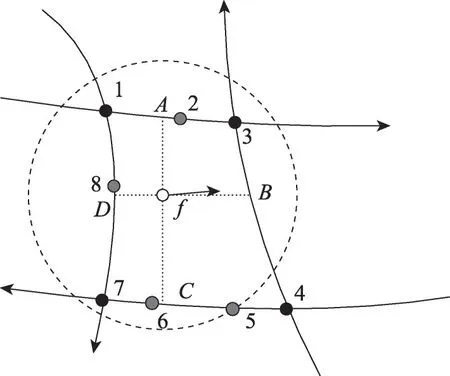
图4 点到线匹配Fig. 4 Point to line matching

将匹配完路段的轨迹点作为待校正轨迹点，将所属为同一出租车下的待校正轨迹点归为一个集合F，即：

其中，F为出租车=的所有待校正轨迹点集合，,,…,f为按时间顺序排列的待校正轨迹点。

依次校正集合F中的待校正轨迹点，校正方法为：以待校正轨迹点f为中心，选取点f前后相邻的轨迹点f与f，如果在相邻点集[f,f,f]中至少存在两个相邻点匹配的路段相同，则认为轨迹点f路段匹配正确；如果点f与f、f的匹配路段不同，则将待校正轨迹点f的匹配路段校正为f与f所匹配的路段。

再分别计算点与匹配路段中候选点距离，将距离最小的点作为路网中的潜在上车点。

2.3 同时段同点推荐量约束

将乘客集合内的个体按照其叫车时间r进行升序排列，即：

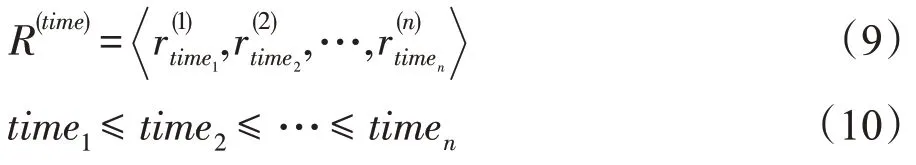
以固定时间间隔将集合)中的乘客划分为不同时段的子集，即：

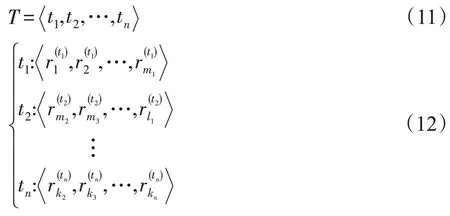
式（11）表示时段集合，式（12）表示在各时段内所采集的乘客集合。

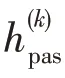
直至其计数值达到分配人数阈值时，该上车点将不作为候选上车点参与计算分配给乘客。即：

2.4 高差值优先算法生成乘客推荐次序

对于同时段内同上车点的乘客推荐次序问题，本文提出了高差值优先算法。

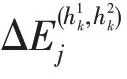
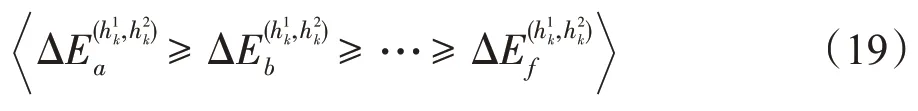
输入：上车点集合；时段乘客集合。

输出：乘客对应乘车点。

其具体推荐流程如图5所示。

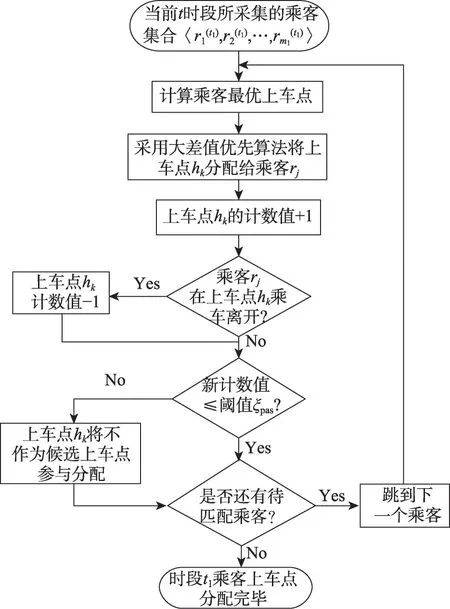
图5 控制订单量流程图Fig. 5 Flow chart of order quantity control

3 实验与分析

本实验分别从乘客与司机角度出发，提供两种优先级策略，分别为乘客优先策略（passenger priority strategy，PPS）和司机优先策略（driver priority strategy，DPS）。探究两策略优劣并与步行距离推荐策略（walking distance recommendation strategy，WDRS）及路况推荐策略（road condition recommendation strategy，RCRS）对收益以及出行时间的影响进行综合比较。

3.1 实验环境

本文所用到的数据集是上海市出租车单日24 h GPS 数据集，数据采集频率为每次10～80 s。实验部分采用Python语言，实验环境、实验参数分别见表2、表3。

表2 实验环境Table 2 Experimental environment

表3 参数设置Table 3 Parameter setting

上述参数值综合考虑真实应用环境与大量实验的最优输出而设定，参数敏感性分析见3.3节。

本文主要采用层次分析法来实现权重的分配。首先通过一致矩阵法构造评分矩阵，从而定义一致性指标与一致性比率，即：

其中，()为矩阵的最大特征值，为矩阵的维数，为矩阵的一致性标准，当＜0.1 时，则判定矩阵具有满意的一致性，则可以对矩阵采用规范列平均法得到所求权重分配。表3 中的∂、、λ、λ及表4 与表5 中的权重分配都采用该方法得出。

3.2 实验结果

PPS实验权重设置见表4。

表4 PPS实验权重设置Table 4 Weight setting in PPS experiment

乘客2 的推荐结果如图6 所示，乘客2 最佳上车点与其他候选上车点收益对比如图7所示，多乘客同时段叫车的推荐结果如图8所示。

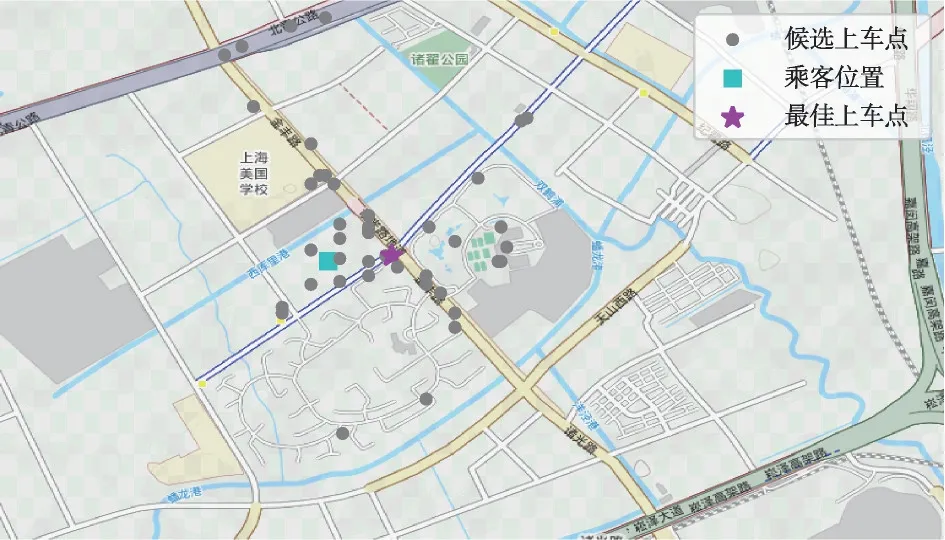
图6 乘客2推荐结果Fig. 6 Passenger 2 recommendation results

如图6 所示，方形点位置为乘客2 叫车位置，综合考虑所有候选上车点的乘客步行收益、司机驾驶收益、上车点路况指标以及上车点附近安全性等关键因素。由于离乘客2 较近的候选上车点的路况指标及安全性较差，综合推荐星形点位置为乘客2的最佳上车点位置。

如图7所示，乘客2的最佳上车点较其他候选上车点有最高的司机驾驶收益和上车点综合收益，但该上车点的路况指标明显低于其他候选上车点水平，且在步行收益方面也较低于某些其他候选点。

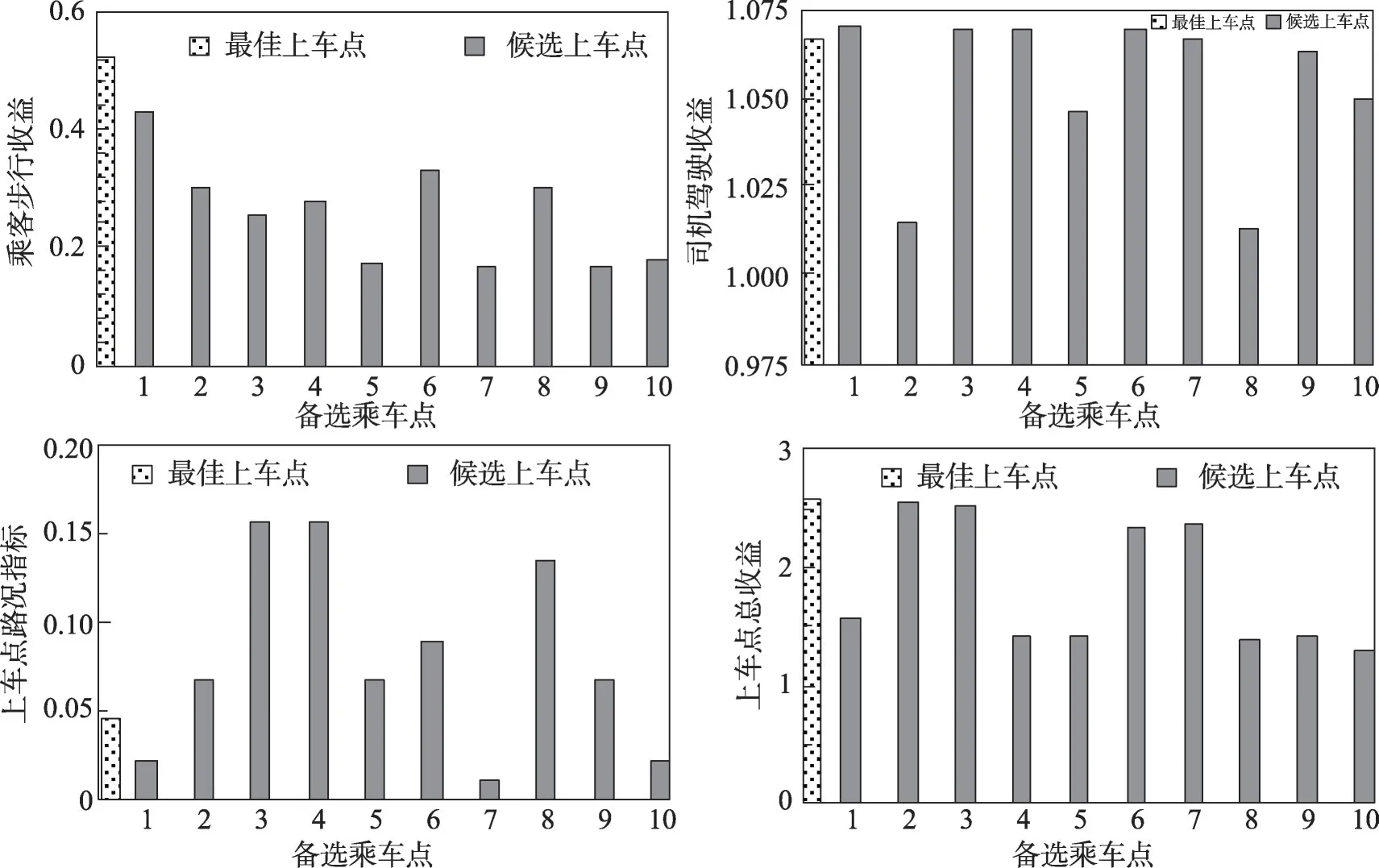
图7 乘客2收益对比Fig. 7 Revenue comparison of passenger 2

如图8所示，推荐给乘客的上车位置都距离乘客较近，当多乘客同时叫车时，除考虑所有备选上车点的各项收益外，还要约束控制同时段同一上车点的推荐次数，实现上车点有序、有效地分配。

图8 多乘客推荐结果Fig. 8 Multi-passenger recommendation results

DPS中参数权重设置见表5。

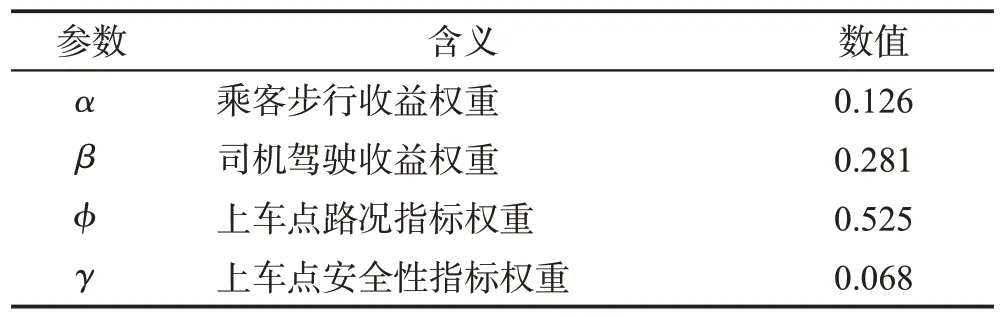
表5 DPS实验权重设置Table 5 Weight setting in DPS experiment

乘客2 的推荐结果如图9 所示，乘客2 最佳上车点与其他候选上车点收益对比如图10 所示，多乘客同时段叫车的推荐结果如图11所示。

图11 多乘客推荐结果Fig. 11 Multi-passenger recommendation results

如图9 所示，由于离乘客2 较近的点安全性、路况等指标较差，综合考虑，推荐拥有较高路况指标且安全性较高的星形点位置为乘客2 的最佳上车点位置。

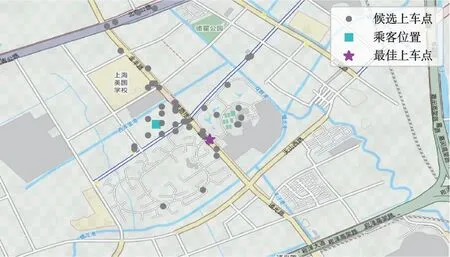
图9 乘客2推荐结果Fig. 9 Passenger 2 recommendation results

如图10 所示，乘客2 的最佳上车点较其他候选上车点有较高的司机驾驶收益和路况指标。

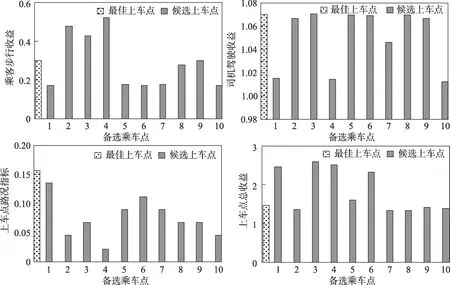
图10 乘客2收益对比Fig. 10 Revenue comparison of passenger 2

如图11 所示，推荐给各乘客的最佳上车点都拥有较高的路况指标，且安全性较高。当多乘客叫同时段车时，除考虑各收益外，还要约束控制同时段同一上车点的推荐次数，实现上车点有序、有效地分配。

本实验从司机与乘客双方角度出发，探究司乘双方的收益关系及各方收益的变化趋势，如图12所示。

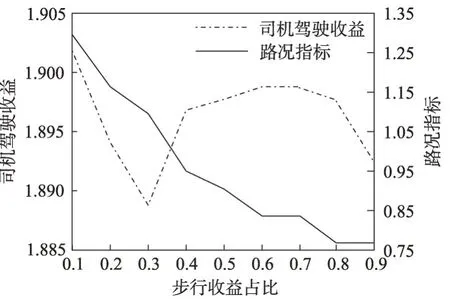
图12 司乘收益分析图1Fig. 12 Driver and passenger income analysis figure 1

如图12所示，在提升乘客步行收益占比时，路况指标下降明显，且当步行收益占比在0至0.3时，司机的驾驶收益大幅下降。

如图13所示，在提升司机驾驶收益的占比时，乘客的步行收益持续下降，而路况指标则持续提升。

图13 司乘收益分析图2Fig. 13 Driver and passenger income analysis figure 2

如图14所示，在提升路况指标占比时，乘客的步行收益也会受影响而持续下降，而当路况指标占比小于0.25时，司机的驾驶收益呈下降趋势，当路况指标占比在0.25～0.40 时，司机驾驶收益呈稳定上升趋势。

图14 司乘收益分析图3Fig. 14 Driver and passenger income analysis figure 3

3.3 结果分析

（1）综合收益分析

不同策略的上车点推荐结果对比见表6。

由表6可知，在乘客步行收益方面，WDRS具有一定优势，RCRS则效果较差，与WDRS相差1.53；在司机驾驶收益方面，PPS 优于其他，RCRS明显低于其他水平；在路况指标方面，RCRS表现出明显优势，与效果最差的WDRS相差0.07；在综合收益方面，PPS比平均综合收益最低的RCRS高1.74。

表6 上车点收益表Table 6 Revenue of pickup point

（2）行程时间对比

本文以人的平均步行速度60 m/min，出租车的平均行驶速度600 m/min 进行实验，实验结果见表7。

由表7 与图15 实验结果可知，在乘客步行时间方面，WDRS的时间明显少于其他方案；司机接驾时间方面，PPS 与WDRS时间略短，RCRS接驾时间较长；路程时间方面四种策略表现相当。行程总时间方面，PPS、DPS、WDRS时间相差不大，但RCRS时间较长。

图15 时间对比图Fig. 15 Time comparison chart

表7 行程时间表Table 7 Travel schedule min

（3）敏感度分析

本文通过对步行收益、驾驶收益、路况指标、安全性指标在目标函数中的占比，分析各指标对复合收益的影响，实验结果如图16所示。

如图16 所示，随着步行收益与路况指标占比增加，复合收益水平会明显降低；随着司机驾驶收益与安全性指标占比增加，复合收益水平会有大幅度提高。

图16 敏感度分析Fig. 16 Sensitivity analysis

4 结束语

本文通过对时空轨迹大数据进行归纳与分析，挖掘出乘客历史上车点，综合考虑乘客步行收益、司机驾驶收益、上车点路况指标、周边安全性等关键因素，建立上车点的复合收益评价，构建最佳上车点的动态推荐模型。并提出一种高差值优先算法，解决同上车点乘客的推荐次序问题，实验证明本文算法可以使上车点实现高效有序的分配，且PPS与DPS推荐策略在综合收益方面明显好于WDRS与RCRS推荐策略。在时间方面，PPS的接驾时间与路程时间最短，WDRS的步行时间最短。行程总时间方面，PPS、DPS、WDRS时间相差不大，但RCRS时间较长。

未来研究中，仍需要进一步探索本文提出的四项指标对于最佳上车点选取的具体影响，并以动态方式决定该四项指标在最佳上车点推荐模型中的占比。