移动边界域上一类退化波动方程的高精度格式*
2022-07-20谢伟松何振鹏
刘 颖,谢伟松**,何振鹏
(1. 天津大学数学学院,天津 300354;2. 中国民航大学航空工程学院,天津 300300)
0 引 言
现代科学、技术和工程中的大量问题的数学模型都可以用偏微分方程来表示,大多数自然科学问题的基本方程本身就是偏微分方程.但是,绝大多数偏微分方程定解问题的解不能以实用的解析形式来表示.如果方程的形式复杂,或者求解区域的形状复杂,其解析解就更难以得到.这就需要寻找偏微分方程定解问题的近似解,也就是数值解.
随着计算机技术的飞速发展,微分方程的数值解法得到了前所未有的发展和应用.有限差分法是求解偏微分方程定解问题的主要数值方法之一[1-3],此方法已经有了比较成熟的算法格式和软件,并能对其进行比较完善的理论分析.目前,利用有限差分法求解双曲型方程的研究成果比较丰富. Bou‐jaoui 等[4]研究了一维波动方程边界反馈问题的有限差分离散方法,并证明了解的能量是呈指数衰减的;Boujaoui[5]研究了具有内阻尼的一维波动方程的有限差分全离散形式,并利用可观测不等式证明了阻尼系统能量的衰减率一致依赖于网格长度;Wang 等[6]采用有限差分法对时变偏微分方程尤其是二阶波动方程进行数值求解,采用具有守恒性质的有限差分算子对内点进行数值离散,同时采用相关的离散方法对边界和网格界面条件进行处理,得到了精度较高的数值实验结果.现有文献多数都是在非移动边界域[4-20],也就是固定区域上进行的研究.针对移动边界域上的研究相对较少,本文研究内容相对于在非移动边界域上的研究难度加大,是实际工程问题中的一个难题.本文将采用有限差分方法在移动边界域上对一类退化波动方程的数值解法进行研究,并给出2 种数值求解该类方程的差分格式.这2 种差分格式对时间的离散均采用二阶中心差分格式,对空间的离散分别采用二阶差分和四阶差分格式,其截断误差分别为O(τ2+h2)和O(τ2+h4).同时进行相应的数值模拟,给出具有一定精度的数值实验结果.
1 问题陈述
本文主要利用有限差分法研究移动边界域上一类退化波动方程的数值解法,考虑下述非齐次初边值问题

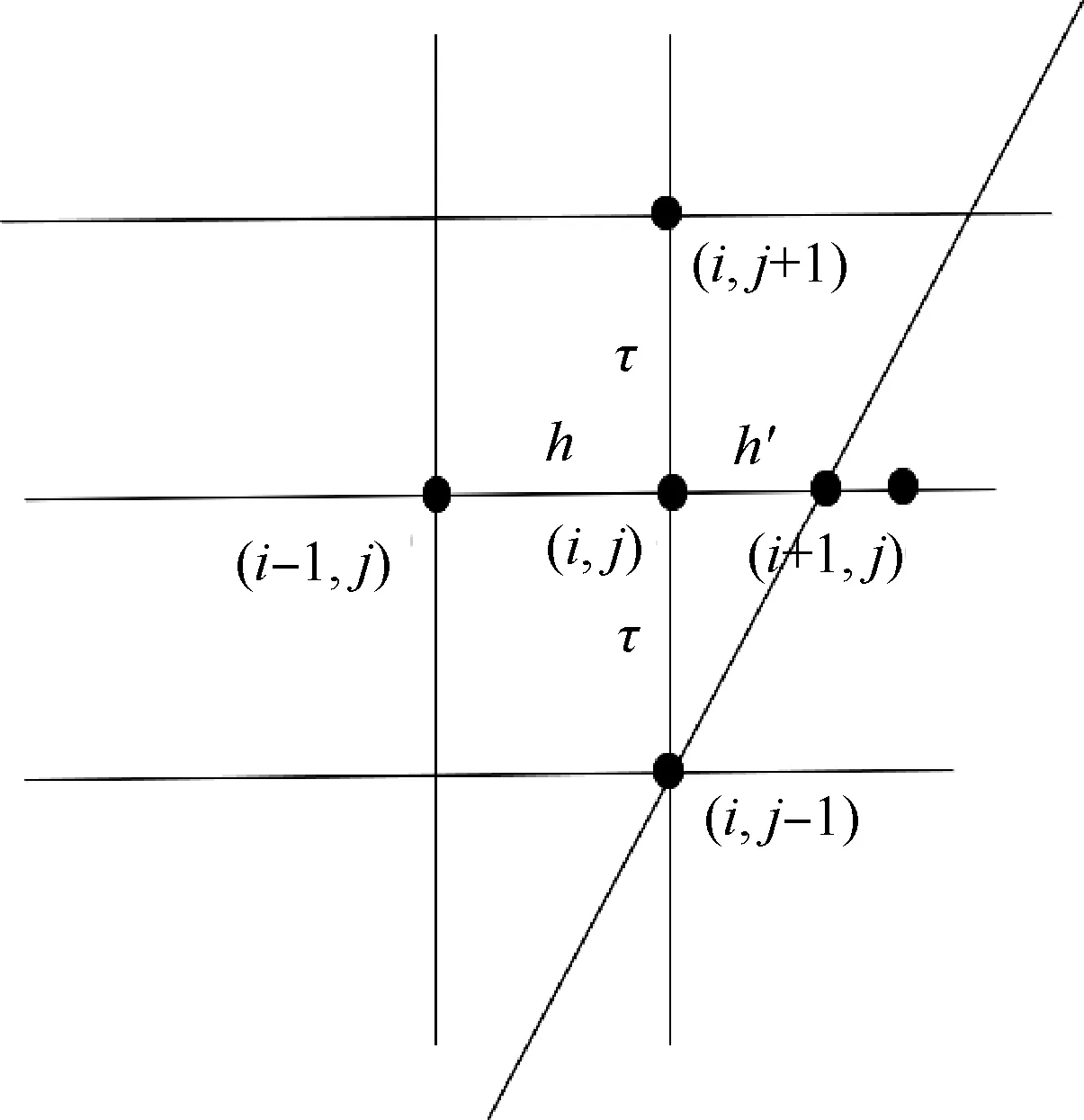
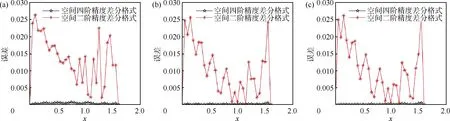
式中:xp为非线性系数;0 为了使用有限差分法求解问题(1)~(3),将求解区域 进行剖分.取正整数m和n,并记 本文后面涉及到第j层节点都以此为标准. 定义Ωτh上的网格函数 图1 网格剖分 式中 在内部矩形网格节点处考虑方程(1),有 代入(4)并忽略高阶无穷小量O(τ2+h2),得到 由初值条件(3),有 由方程(1),可知 根据带积分余项的Taylor 展开式以及式(3),可得 在边界x=lk(t)上的非矩形网格处采用非等距差分格式(图2).如果边界点左侧的节点记作(i,j),右侧节点记作(i+ 1,j),点(i+ 1,j)实际不在求解域上.因为边界右侧节点不在求解域上,对于求解域外矩形网格点不编号,将边界点编号记作(i+1,j). 图2 非等距差分格式 忽略高阶无穷小量O(τ2+h2),得到方程(1)的差分格式: 式中h′如下: 首先将方程(1)改写为 为保证四阶精度,利用待定系数法得到uxx和ux的计算公式 式(14)即为求解退化波动方程(1)的时间二阶精度、空间四阶精度的差分格式.此格式为一个7 点格式,对于空间方向第2 层以及距离斜边1 个点和2 个点处无法利用此格式,还需要单独建立其差分格式. 对于空间第2 层处差分格式,同样采用待定系数法求得uxx和ux的计算公式 将上式和式(13)代入式(10)并忽略高阶无穷小量O(τ2+h4),整理得 对于距离斜边2 个点处差分格式,同理可得 对于距离斜边1 个点处的值,则不易采用待定系数法求得差分格式,本文采用相应精度的插值法进行计算. 通过数值模拟方法分别给出2 种差分格式下离散问题的解,并进行数值计算.文中所涉及到的误差定义如下:最大绝对误差 初值条件u(x,0) =φ(x) = ex,ut(x,0) =ψ(x) = ex,边值条件u(0,t)=α(t)=et,u(lk(t),t)=β(t)=elk(t)+t,即 该问题的精确解为u(x,t) = ex+t. 令p=0.5,k=0.2,T=3,通过数值模拟可以得到问题的数值解,同时可以得到精确解的图像(图3). 图3 精确解的图像 当h=0.05,τ=0.025、0.012 5、0.006 25 时,使用空间二阶精度差分格式和空间四阶精度差分格式所得误差结果如图4 所示.结果表明:用这2 种差分格式得到的数值解与精确解非常接近,绝对误差也比较小.因此,该差分格式符合实际需要,验证了2 种差分格式的精确性. 图4 不同时间步长时2 种差分格式得到的数值解与精确解的误差图像 当t=T= 3,空间步长为0.05,时间步长分别为0.025、0.012 5 和0.006 25 时,采用空间二阶和四阶精度差分格式所得数值解的绝对误差对比曲线如图5 所示.空间四阶精度差分格式的绝对误差比空间二阶精度差分格式的绝对误差更小,说明空间四阶精度差分格式优于空间二阶精度差分格式. 图5 2 种差分格式误差比较 当h= 0.05,τ= 0.025 时,空间二阶和四阶精度差分格式所得数值解的最大绝对误差分别为0.041 5和6.930 3×10−4;当h=0.05,τ=0.012 5时,2种差分格式对应的最大绝对误差分别为0.025 8 和4.931 3×10−4;当h= 0.05,τ= 0.006 25 时,2 种差分格式对应的最大绝对误差分别为0.026 3 和5.168 1×10−4.可知,步长相同时,空间四阶精度差分格式最大绝对误差比二阶的更小,并且空间二阶精度差分格式的最大绝对误差达到了10−2,而空间四阶精度差分格式的最大绝对误差能达到10−4,更加充分地说明空间四阶精度差分格式比空间二阶精度差分格式具有更高的精确性. 本文利用有限差分法研究了移动边界域上一类退化波动方程的数值解法,针对此类退化波动方程,对时间方向的离散采用二阶中心差分格式,对空间方向的离散分别采用二阶和四阶差分格式.最后通过数值模拟验证了有限差分法在解决此类问题时是有效可行的,且空间四阶精度差分格式比空间二阶精度差分格式具有更高的精确性.2 差分格式
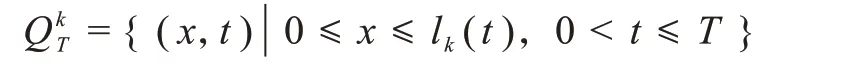





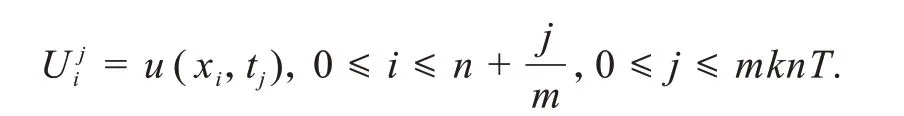
2.1 二阶精度差分格式
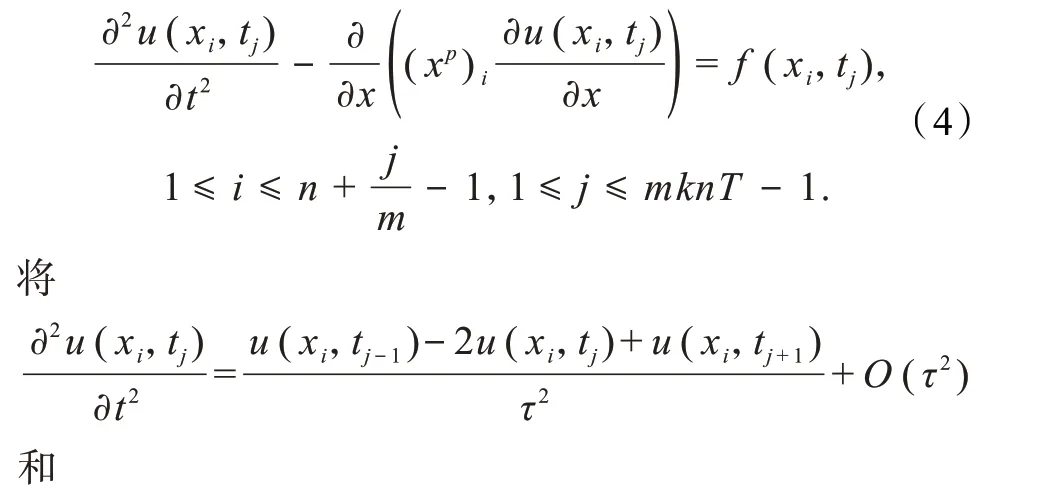

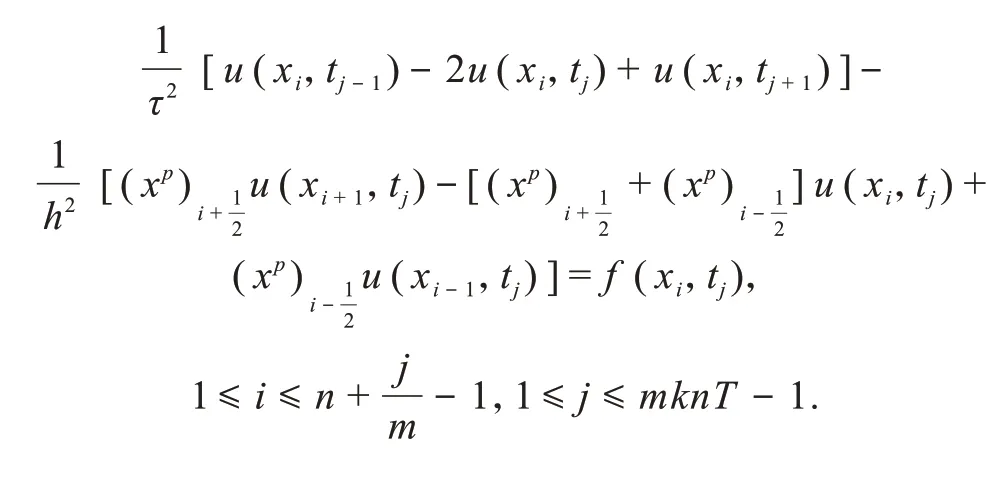

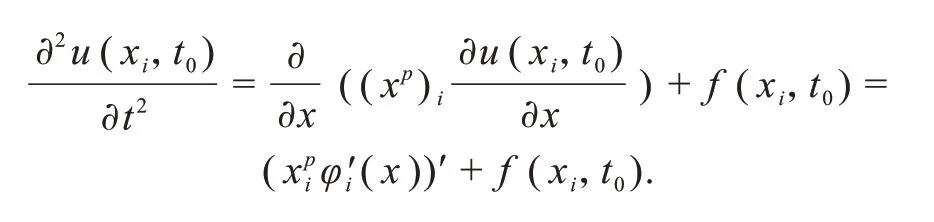




2.2 四阶精度差分格式
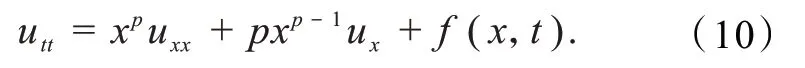

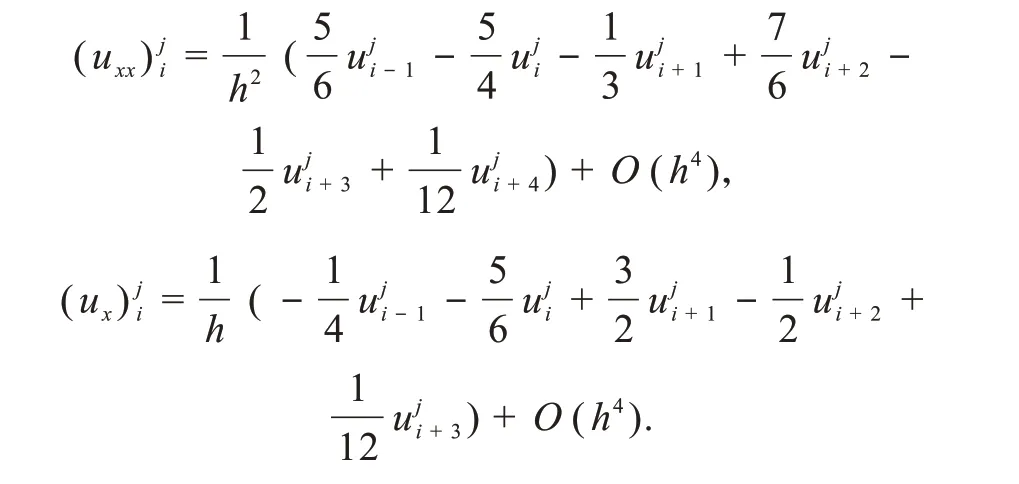

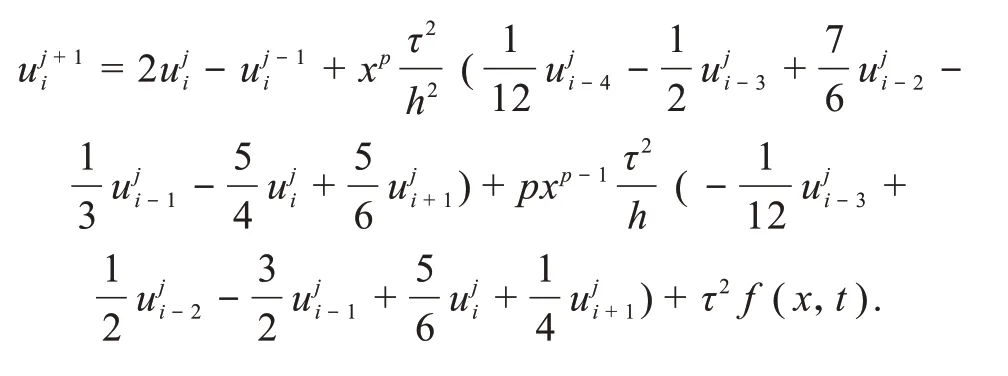
3 格式检验




4 结束语
