计及频率的电力系统概率潮流计算
2022-07-20汪承茂李进军廖星星
汪承茂,袁 伟,李进军,张 威,廖星星
(1.南京南瑞继保电气有限公司,江苏 南京 211102;2.中国电建集团江西省电力设计院有限公司,江西 南昌 330096)
0 引言
2020年,为响应国际气候形势,中国相继提出“新型电力系统”、“双碳”目标[1],在此背景下,可以预见未来新能源将成为我国主要能源。然而,规模化新能源接入必将导致电网呈现强随机性,从而给系统安全稳定运行带来挑战,因此,有必要对其存在的不确定性进行量化分析,从而进一步评估给电网带来的风险。
文中基于概率潮流思想,对电网进行不确定性分析,概率潮流最早由国外学者1974年提出[2],演变至今,其主要计算方法可分为模拟法[3]、近似法[4]、解析法[5-6]和人工智能法[7-8]四大类。其中,解析法中的半不变量法由于可以快速求得系统变量的概率信息,因此受到广泛应用。
基于上述分析,文中首先建立了考虑一次频率特性的常规发电机、负荷和新能源功率模型。其次,针对输入变量的功率不确定性,采用具体模型拟合新能源(主要考虑风电)和负荷的功率曲线。接着,为求得输出变量的概率分布信息,提出了计及频率的概率潮流计算方法。最后,在改进的标准节点系统中验证了所提方法的有效性。
1 计及频率的电力系统潮流模型
为计算系统频率的概率分布特性,首先需要在稳态潮流模型的基础上加入频率变化特性,其各模块的一次调频模型如下所示。
1.1 基于下垂控制的新能源出力模型
考虑一次调频特性并且基于下垂控制方式,新能源出力模型可表示成如下形式:
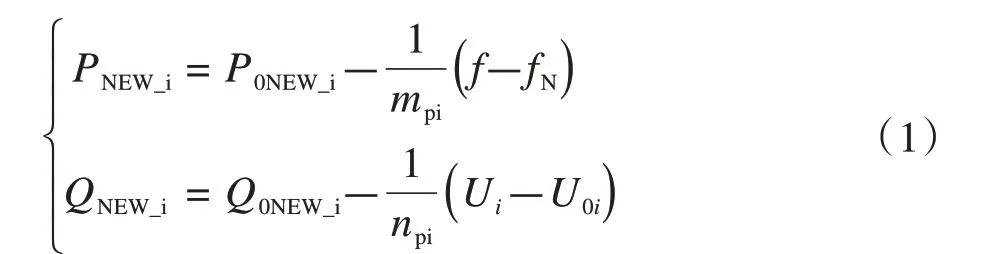
式中:PNEW_i表示新能源接入系统的有功功率;P0NEW_i表示新能源的额定有功功率;QNEW_i表示新能源接入系统的无功功率;Q0NEW_i表示新能源的额定无功功率。U0i表示空载电压;Ui为节点i运行电压;mpi为系统频率;f为系统额定频率;fN表示新能源有功下垂增益;npi表示新能源无功下垂增益。
1.2 发电机、负荷的一次调频模型
考虑一次调频特性,计及发电机的频率调节模型可表示为:
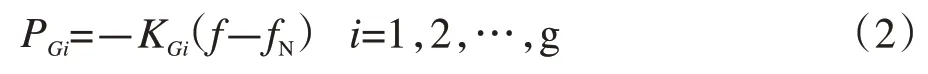
式中:PGi表示系统第i台发电机的有功出力,KGi表示其一次调频系数。
考虑负荷参与系统一次调频,假设第节点的负荷在系统频率f和fN下的负荷功率分别为PDi和PDNi,其一次频率调节特性可表示为如下表达式:

式中:KDi表示一次调频系数。
1.3 考虑一次调频的电力系统潮流模型
将上述模型进行整理分析,可以得到如下等式:
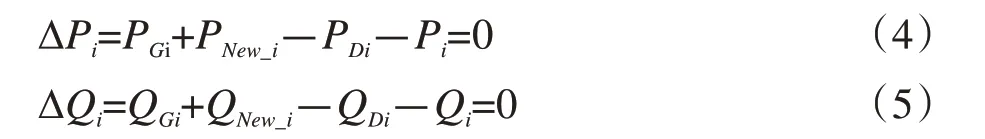
式中:ΔPi为节点 的有功不平衡量;ΔQi为节点i的无功不平衡量;QGi为发电机无功出力;QDi为负荷无功功率;Pi表示系统有功方程;Qi表示系统无功方程。
进一步结合式(1)-(5)建立起联合表达式,具体模型如下:
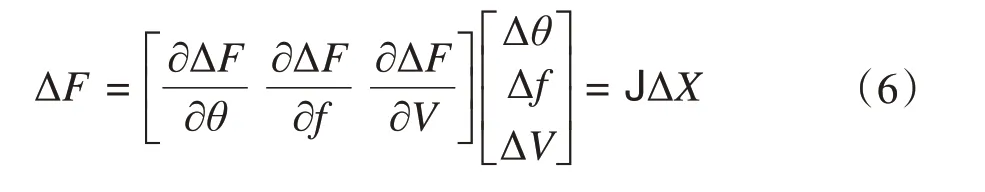
式中:ΔF、ΔX为变量的输入和输出修正量;Δθ、ΔV和Δf为相角、电压和频率修正量;J为雅克比矩阵。
2 风电出力和负荷不确定性模型
2.1 基于高斯混合模型的风电出力模型
考虑规模化新能源(由于风电不确定性较大,因此文中主要考虑风电)接入至电力系统中,因此其随机源主要有负荷和风电。目前,风电出力的随机性通常采用威布尔分布描述,然而,随着系统中变量的随机性进一步加剧,采用传统的模型函数难以对其概率分布进行拟合,而概率潮流计算对于输入随机变量的概率分布描述极为敏感,其准确程度直接影响最终的计算结果,基于以上需求分析,文中采用高斯混合模型对变量进行拟合,其具体计算流程如图1。
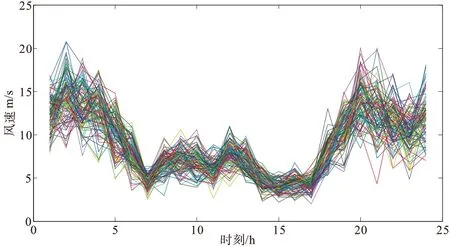
图1 多时段风速波动曲线
高斯混合模型其具体概率密度函数为:
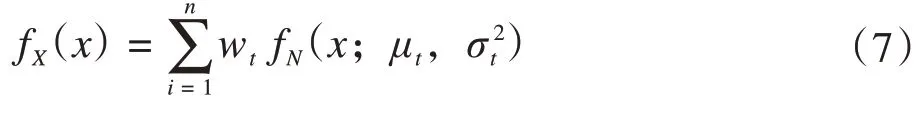
式中:fX(x)表示随机变量的概率密度函数;wi、μt和σt分别表示第t个高斯子成分的权重、期望值和标准差;n表示子成分个数;fN(·)为正态分布函数。
上式中权重参数wt需满足归一化条件,表示如下:

引入极大似然估计高斯子成分参数wt、μt和σt,对数似然函数L如下:
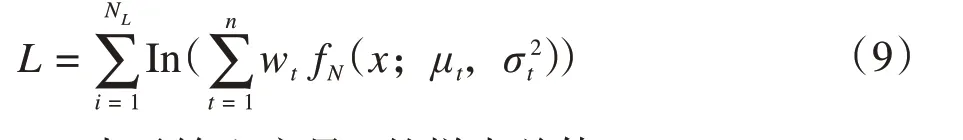
式中:NL表示输入变量xi的样本总体。
2.2 负荷的有边界正态分布模型
负荷不确定性通常可采用正态分布函数描述,但由于实际负荷存在最小值和最大值,因此文中采用有边界的正态分布函数对其不确定性进行建模,其模型具体如下:

式中:Pmin和Pmax分别为有功负荷的最小和最大值;Qmin和Qmax分别为无功负荷的最小和最大值;μ和σ分别表示负荷的期望和标准差,可根据实际情况取期望的5%~10%。
3 基于半不变量法的电力系统概率潮流计算
针对新能源接入系统后对电网产生的影响,为准确获取系统输出变量中电压、频率等的概率分布信息,提出了基于半不变量法的概率潮流计算方法。
3.1 半不变量法
式(6)中建立了系统输入、输出关系式,以此为桥梁将其进行简单变换即可得到半不变量计算公式,具体如下:
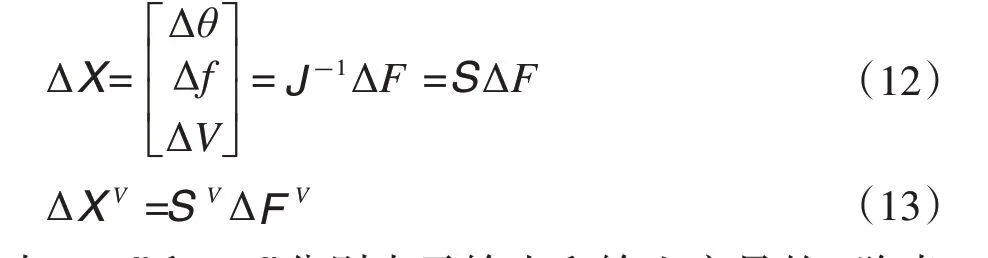
式中:ΔXV和ΔFV分别表示输出和输入变量的v阶半不变量;S为灵敏度矩阵。
因此为使得计算更加接近实际运行场景,文中在计算概率潮流过程中,进一步考虑相关性,其相关性样本产生的方法如下[9]:
1)得到一个不具有相关性的标准正态分布矩阵Vn1。
2)对其相关系数ρ变换得到新的系数矩阵ρ1并进行Cholesky分解:

式中:G1表示分解后得到的矩阵。
3)进一步,求得系数矩阵为ρ1的标准正态分布矩阵:

4)最后,通过Nataf变换得到随机变量样本Xn1,此时该样本的相关系数矩阵仍然为ρ,即为所需的样本,具体公式如下所示:

式中:F-1(Φnorm(·))表示正态分布的反函数。
通过上述方法得到随机变量的相关性样本后,再进行相应的灵敏度矩阵修正即可计及相关性对系统的概率潮流进行计算[5]。
3.2 Cornish-Fisher级数展开
基于上述概率潮流计算方法得到输出变量的各阶半不变量后,可以对其概率密度曲线进行拟合,目前常用的拟合方法有Gram-Charlier级数展开和Cornish-Fisher级数展开。由于Gram-Charlier级数展开在拟合概率分布曲线时在首末两端容易出现概率小于0或大于1的反常情况[10],而Cornish-Fisher级数展开有效的克服了这一缺点,因此文中采用该方法进行曲线拟合。
Cornish-Fisher级数拟合公式与变量的各阶半不变量有关,其具体公式如下:
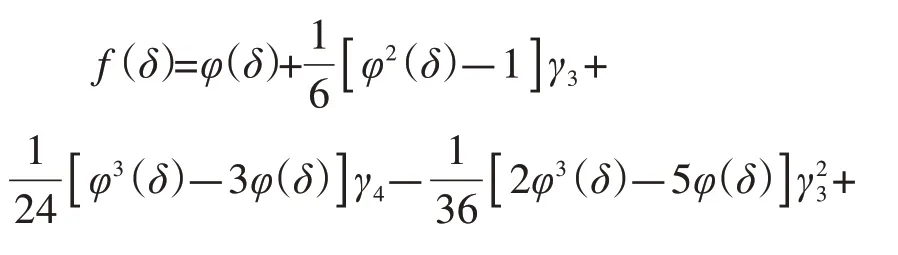
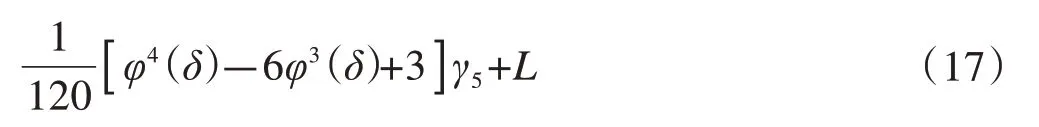
式中:f(δ)为变量标准化后的概率密度函数;φ(δ)为φ的概率密度函数;γi=(i=1,2,3,k)为各阶半不变量。
基于上述计算后,即可得到计及频率的概率潮流计算流程,具体如图2。
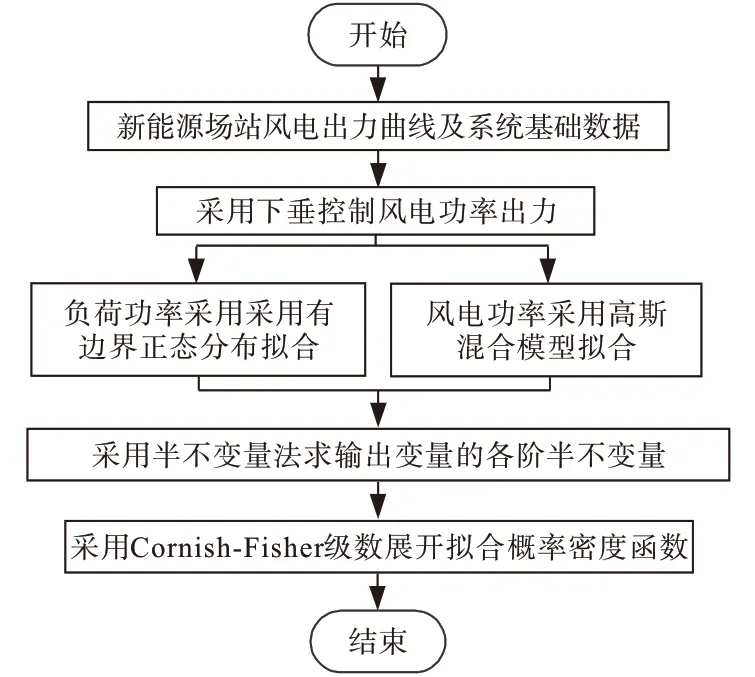
图2 计及频率的电网概率潮流计算流程图
4 算例分析
4.1 算例参数说明
以改进的IEEE-57节点系统算例进行测试分析,在节点33、44、49、50分别接入50 MW风力发电系统,为便于计算其各风电场之间的相关系数取0.5。风电场输出功率概率特性通过实际输出功率进行高斯混合模型拟合得到,其各分量如表1所示,其部分拟合图像如图3所示。风电场站功率之间的相关系数矩阵可由实际数据求得。假设负荷波动期望为其预测值,标准差取期望的10%。表2给出了部分参数的设置范围[10-11]。
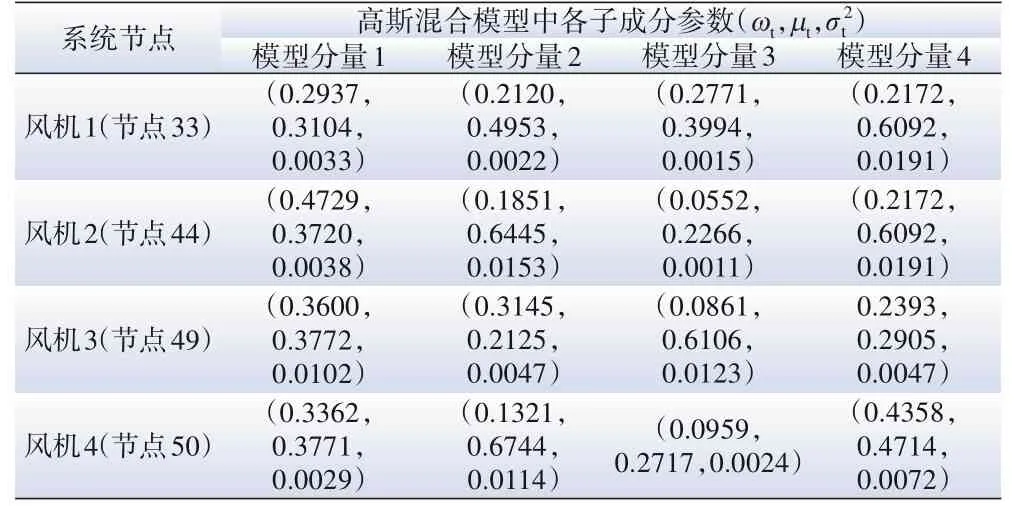
表1 风电高斯混合模型拟合及其各分量

表2 参数设置
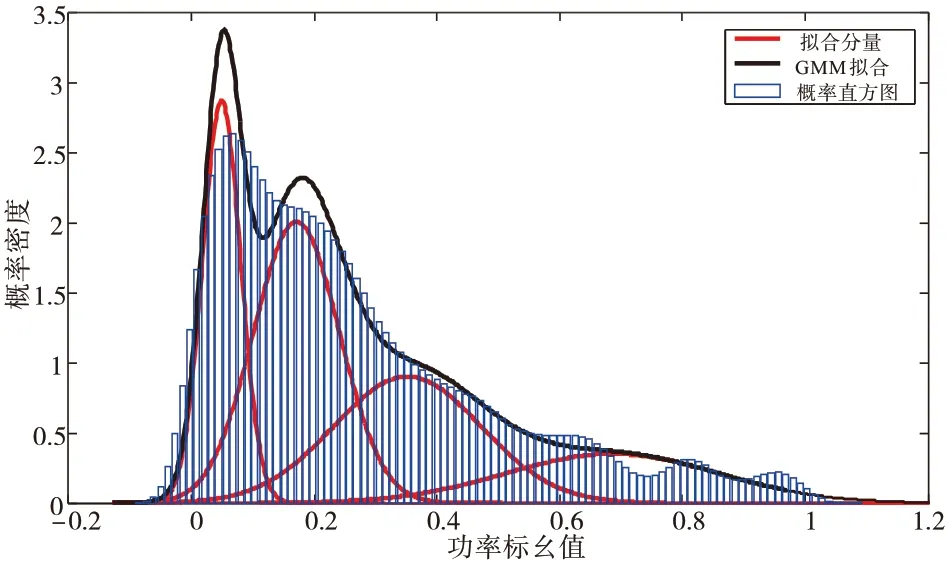
图3 风电功率高斯混合模型拟合示意图
4.2 算法有效性分析
为验证所提方法有效性,本文概率潮流计算结果以蒙特卡罗模拟法为基准,即将其进行10 000次循环计算,通过MATLAB等求得其概率信息。
(1)期望值和标准差的相对误差值:

式中:表示相对误差值;x表示输出变量;η表示随机数字特征;表示半不变量法计算结果;表示蒙特卡罗模拟法计算结果。
(2)输出变量的方差和的根均值指标[12]:
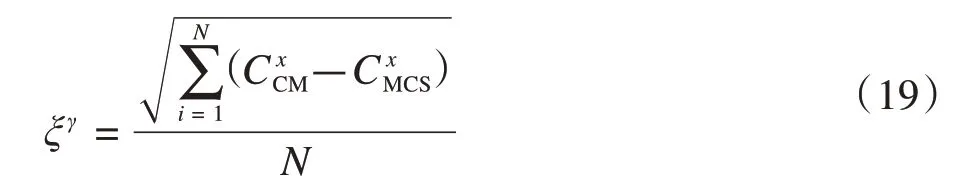
式中:ξγ表示ARMS指标和分别为采用半不变量法和蒙特卡洛模拟法所得概率密度曲线上第i点的值;N表示取点个数。
表3为文中所提方法的计算结果误差,其中和分别表示期望相对误差的平均值和最大值,和分别表示标准差相对误差的平均值和最大值。从表中分析可得,所提半不变量法计算频率时的最大误差为4.783%,计算电压的最大误差为3.683%,所得结果充分表明半不变量法计算的准确性,符合目前实践计算所要求的计算精度。

表3 所提方法计算结果误差
表4为系统变量的根均值指标,其中和分别表示其最大值和最小值,从表中计算结果分析,频率计算的最大误差为4.973%,电压计算的最大误差为4.256%,从该指标的降低进一步反映了所提方法的有效性。

表4 所提方法计算结果的根均值指标
为进一步验证所提方法的准确性,图4和图5分别为节点电压和频率的概率分布曲线,表5为节点50电压及频率的前七阶半不变量,从图、表中可以看出,文中所提半不变量法与作为基准值比较的蒙特卡洛模拟法结果较为相近,具有较好的实用性。同时,在计算效率方面,蒙特卡洛模拟法需要356.7 s,而半不变量法仅为3.6 s,前者是后者的近百倍,因此所提方法在计算效率上也具有明显优势。
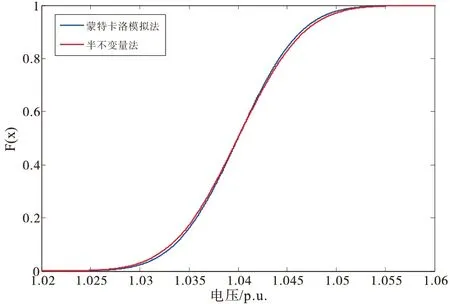
图4 节点50电压概率分布曲线
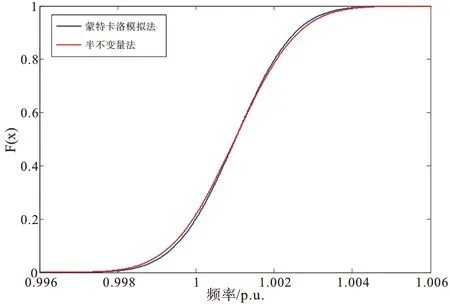
图5 频率概率分布曲线
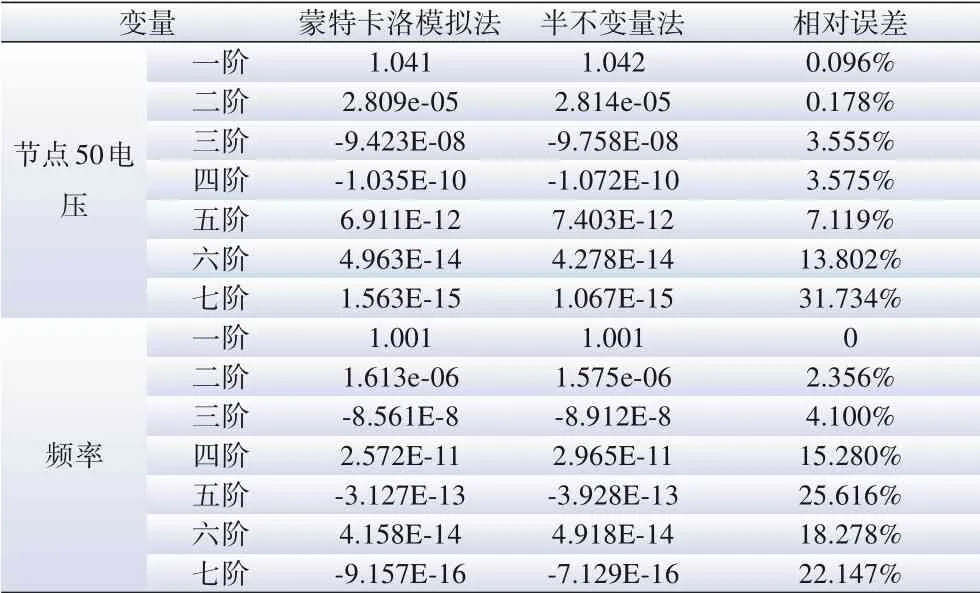
表5 节点50电压及频率的前七阶半不变量
4.3 不同风电渗透率对电网的影响
考虑不同风电渗透率对系统频率的影响,设置不同渗透率场景:不接入新能源(0),低渗透率(13.79%),高渗透率(32.42%)。图6和图7分别给出了不同渗透下节点50电压概率密度曲线和频率概率密度曲线。从图中分析,新能源渗透率越大时,电压和频率波动幅度越大。
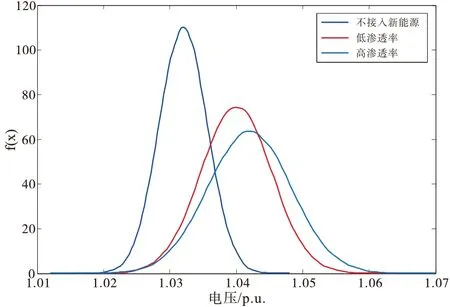
图6 不同渗透率下节点50电压概率密度曲线
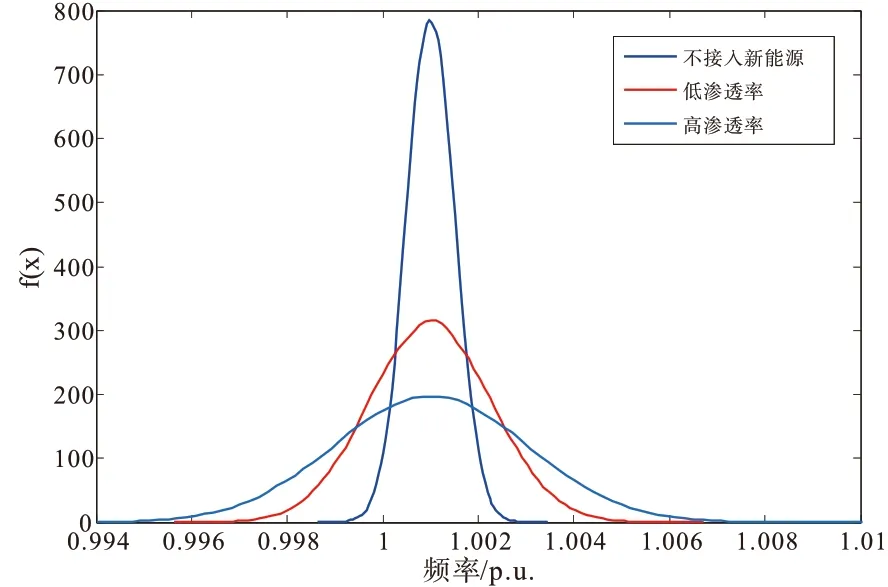
图7 不同渗透率下频率概率密度曲线
进一步定量分析变量在不同渗透率下的越限概率,表6为不同渗透率下变量越限水平。对于频率,不接入新能源时越限概率为0,低渗透率时越限概率为0.89%,高渗透率时越限概率为6.60%;对于电压,不接入新能源时越限概率为0,低渗透率时越限概率为3.03%,高渗透率时越限概率为9.84%。基于上述图表分析,在规模化新能源接入的高渗透率场景下,系统变量越限需要引起足够重视。

表6 不同渗透率下变量越限水平
5 结语
文中为准确得到电网电压、频率等输出变量的概率分布信息,在考虑风电、负荷等功率不确定性的基础上提出了一种计及频率的电力系统概率潮流计算方法。通过算例分析充分表明所提方法的有效性、快速性,同时,计算得到的结果可以为调度运行人员提供参考依据,为后续风险评估、随机优化研究奠定坚实基础。
