轴箱弹簧动刚度频变特性对机车振动响应影响
2022-07-20马呈祥陈相旺姚远陈吉永赵清海
马呈祥,陈相旺,姚远,陈吉永,赵清海
(1.中车大同电力机车有限公司 技术中心,山西 大同 037038;2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
1 概述
轴箱弹簧是铁道车辆一系悬挂的重要组成部分,承载着构架上部的载荷,同时缓冲隔离线路不平顺引起的冲击与振动,是保障列车动力学性能和运行品质的关键悬挂元件。列车实际运行中,轴箱弹簧工作条件复杂,近年来更是出现多起弹簧断裂事故,严重影响机车车辆正常运行[1-5]。因此有必要对轴箱弹簧自身振动及其对机车车辆振动传递的影响开展深入研究。
在传统机车车辆振动分析中,弹簧往往被等效为刚度为常数的力元引入动力学模型,忽略其自身质量和振动行为[6]。实际上,在低频激励下弹簧刚度特性随激励频率变化较小,但在中高频激励下弹簧刚度会随激励频率的变化而显著变化[7-8]。
针对弹簧刚度频变特性已开展了诸多研究。孙文静等[9-10]运用动刚度矩阵法求解高速车辆轴箱弹簧的动刚度特性,结合高速车辆-轨道耦合动力学模型,分析其对车辆及轨道振动影响,以及车辆-轨道系统耦合效应对一系螺旋弹簧疲劳失效的反作用。成军强等[11]对双卷并联弹簧及弹簧、橡胶垫串联系统进行有限元计算分析,研究预压缩量、激励幅值及弹簧和橡胶材料的阻尼比对弹簧垂向动刚度的影响。尹太国等[12]研究地铁车辆一系钢簧中高频段的动态响应,并分析弹簧固有模态特性、动刚度特性、弹簧动态应力分布特征对弹簧应力的影响。刘丽等[13]采用分布集中质量方法处理钢簧频变特性,研究考虑轴箱弹簧频变特性对高速车辆振动传递特性及直线运行平稳性的影响。目前关于轴箱弹簧频变动刚度特性对机车动力学性能影响的研究还较少,尤其对于特殊工况高频激励下弹簧内部振动对机车振动响应的影响。
建立某型电力机车轴箱弹簧有限元模型,分析弹簧固有模态及频变动刚度特性。并将包含轴箱弹簧质量和刚度信息的柔性体引入机车动力学模型中,研究弹簧动刚度频变特性对机车振动的影响。针对该型机车实际运用中存在明显车轮高阶非圆化磨耗现象,重点对比车轮多边形激励工况下考虑弹簧动刚度频变特性较传统弹簧常刚度模型的机车垂向振动特性差异。
2 轴箱弹簧动态特性
2.1 弹簧有限元模型
研究对象为某8轴电力机车轴箱钢弹簧,一系轴箱采用双拉杆定位方式,轴箱两侧各布置1根螺旋弹簧和1根拉杆。钢弹簧采用等截面圆柱螺旋压缩式弹簧,垂直安装在轴箱外侧弹簧座上。弹簧两端面磨平,具有较高的工作稳定性,其相关参数见表1。
在转向架悬挂元件设计中通常假设螺旋弹簧仅在轴线方向承受载荷,忽略螺旋角影响,弹簧简化静刚度可表示为[14]:

结合表1中参数取值,可得弹簧垂向静刚度为1.12 kN/mm。

表1 轴箱螺旋弹簧主要参数
由于惯量的存在,螺旋弹簧存在一系列内共振。在安装状态下(两端全约束),弹簧的1阶垂向固有频率估算方式如下[14]:

结合表1中参数取值,可得弹簧一阶垂向固有频率为112.3 Hz。
为了详细分析轴箱弹簧的动态特性,根据表1所列弹簧参数,利用有限元分析软件ANSYS建立轴箱螺旋弹簧有限元模型(见图1)。弹簧支撑圈部分采用四面体实体单元进行离散,有效圈部分采用六面体实体单元划分,所有单元均为Solid186单元。弹簧有限元模型节点数为39 721,单元数为12 817。

图1 轴箱螺旋弹簧有限元模型
2.2 固有模态分析
分析螺旋弹簧在落车安装状态的固有模态特性,限制弹簧两端接触表面所有节点的6个自由度,在AW0工况下对弹簧进行预加载后,得到弹簧固有频率(见表2)。弹簧的前9阶振动模态主要表现为垂向压缩、弯曲和扭转,其中,1阶垂向模态固有频率为102.3 Hz,与式(2)估算结果相差不超过10%,验证了仿真模型的可靠性。

表2 轴箱弹簧安装状态的模态频率
2.3 动刚度频变特性
在传统车辆动力学分析中,螺旋弹簧往往被简化为无质量线弹性元件,认为其刚度为一恒定值。实际上,轨道车辆装备的螺旋弹簧其质量体积均较大,在轮轨不平顺引起的中高频激励下,弹簧刚度特性随激励频率的变化而显著变化,在车辆振动传递特性分析中仅考虑弹簧静刚度将产生较大计算误差。
采用上述有限元模型分析弹簧动刚度频变特性,对弹簧下端面施加全约束,在其上端面中心节点沿垂向施加1 mm幅值的位移正弦激励,并约束其他自由度。提取弹簧顶端和底部作用力,除以位移激励幅值可分别得到弹簧点刚度和传递刚度。弹簧动刚度随激励频率变化曲线见图2,可以看出,在低频范围内弹簧动刚度变化很小,静刚度值为1.05 kN/mm,与式(1)计算结果相近;随着激励频率的提高,动刚度峰值、谷值交替出现,总体呈现波动上升趋势。在250 Hz以内的弹簧工作频率范围内,点刚度和传递刚度出现多处刚度值突增的峰值点,此时的激励频率接近弹簧固有振动模态频率,以1阶垂向固有频率处的动刚度效应最为显著,刚度值超过50 kN/mm。随着机车运行速度的不断提高,轮轨不平顺引起的高频激励有可能落在弹簧动刚度敏感区域,进而导致动刚度值较准静态刚度值出现数十倍的剧增,对机车垂向动力学响应产生显著影响,应予以特别关注。

图2 弹簧动刚度随激励频率变化曲线
3 机车刚柔耦合动力学模型
建立考虑弹簧频变刚度特性的机车刚柔耦合动力学模型,以分析其对机车振动特性的影响。首先在有限元软件中完成弹簧柔性体模型的预处理,对弹簧进行模态分析和子结构分析,得到包含有限元模型质量、刚度等物理信息的文件。根据弹簧实际装配关系,将其上下端面中心点作为主节点分别耦合弹簧两端面区域。
采用多体动力学仿真软件SIMPACK建立机车动力学模型,并将弹簧有限元文件转化为SIMPACK可识别的柔性体文件导入模型中(见图3),机车主要参数见表3。机车模型由车体、构架、轮对、牵引电机、轴箱、电机吊杆等刚体及轴箱弹簧柔性体组成。轮对轴箱与构架间采用一系悬挂连接,包括轴箱弹簧、定位拉杆和垂向减振器等;构架与车体间采用二系悬挂连接,包括高圆簧、横向和垂向减振器、横向止挡等。拉杆定位、二系高圆簧、减振器和止挡等采用等效力元建模,充分考虑悬挂元件的非线性特性。电机悬挂方式为轴悬,机车轴重为25 t,轮轨关系采用JM3磨耗型踏面与CHN60钢轨相匹配,轨距为1 435 mm,轨底坡为1∶40,轨道激励采用美国五级谱线路不平顺。

表3 机车主要参数
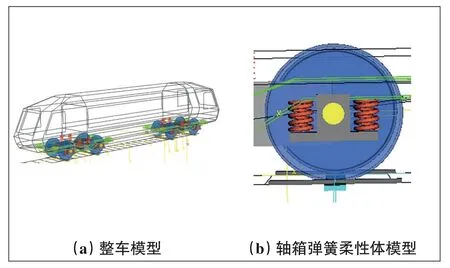
图3 机车刚柔耦合动力学模型
4 机车垂向响应分析
分析轴箱弹簧频变动刚度特性对机车动态响应的影响,对比弹簧分别采用动刚度和常刚度模型引起的机车动力学响应差异。其中,弹簧动刚度模型是包含质量和刚度信息的柔性体模型,能够反映弹簧刚度随频率变化的特性;常刚度模型是对轴箱弹簧采用等效力元处理,弹簧静刚度值保持不变。
弹簧动刚度和常刚度模型仿真结果对比见图4。可以看出,随着运行速度的提高,轴箱、构架和车体的垂向振动加速度均单调递增。2种弹簧模型之间的轴箱加速度响应相差很小,加速度均方根变化曲线几乎重合,可见轴箱垂向振动响应对弹簧动刚度的变化不敏感,忽略弹簧频变刚度特性不会对轴箱响应分析产生很大影响;而二者间的构架振动加速度则存在明显差异,当速度小于90 km/h时,动刚度模型构架垂向加速度较大,速度超过90 km/h后,常刚度模型计算结果较大;2种模型间的车体振动加速度相差较小,动刚度模型的计算结果略小。

图4 弹簧动刚度和常刚度模型的垂向振动加速度仿真结果对比
进一步分析构架振动加速度响应差异,速度80 km/h和110 km/h的构架垂向振动频域分析结果见图5,振动加速度集中在30 Hz以下频段。2种模型的频域响应差异主要体现在0~10 Hz频段,当运行速度为80 km/h时,动刚度模型对应的构架加速度幅值在5~10 Hz频段内大于常刚度模型,得到的时域构架加速度均方根较大;当速度增加到110 km/h后,2种弹簧模型在3~6 Hz内的构架加速度分量显著增大,但常刚度模型的加速度幅值明显大于动刚度模型。由于在1~10 Hz内弹簧动刚度呈小幅递增趋势,落车状态下构架垂向固有模态、侧滚模态也在6~9 Hz频段,因此,即使2种弹簧模型刚度值相差较小,仍会导致构架垂向振动响应的差异。

图5 构架垂向振动频域分析结果
采用不同轴箱弹簧建模方式对机车不同部位振动传递的影响不同。考虑弹簧分布质量和内部振动后,对分析轴箱和车体垂向振动影响较小,而对构架振动加速度影响比较明显。这是由于轮轨振动能量经一系悬挂系统向上传递至构架,考虑轴箱弹簧刚度频变特性后会改变能量的传递特性,进而导致2种弹簧动力学模型的分析结果产生差异。而轮对轴箱系统位于振动传递路径底层,其振动特性变化主要取决于轮轨不平顺输入,受轴箱系统上方弹簧动态特性的影响较弱。另外,二系悬挂隔绝了大部分高频振动,2种弹簧模型间的构架振动加速度差异反映到车体振动响应上不再如此明显。
车轮周向非圆化磨耗即车轮多边形是导致列车轨道大系统宽频带强烈振动和辐射噪声的重要激扰源,不仅影响列车乘坐舒适度,还会引起车辆关键零部件的疲劳断裂,危及行车安全[15]。配属于我国某机务段的该型电力机车在服役过程中频繁出现踏面预报警现象,跟踪测试发现出现踏面预报警的机车存在严重车轮高阶非圆化磨耗,该轮对非圆化测试结果见图6,从阶次粗糙度谱分析结果可以看出,该轮对具有明显的高阶多边形磨耗特征,其中18阶非圆化磨耗最为突出。
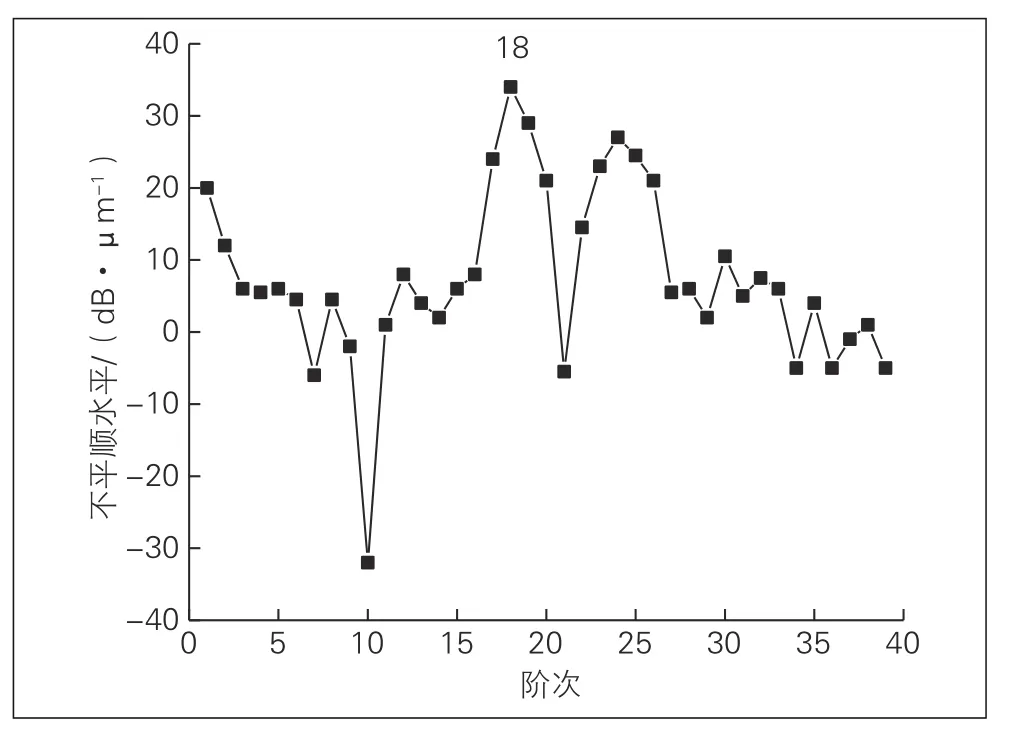
图6 机车车轮非圆化磨耗测试结果
在车轮多边形作用下,列车运行引起的轮轨系统振动频率计算如下:

式中:n为车轮多边形阶数;v为行车速度,km/h;D为车轮滚动圆直径,该机车车轮的名义滚动圆直径为1.25 m。
高阶车轮多边形磨耗会给列车带来高频激扰输入,以18阶多边形为例,当机车以50~120 km/h速度运行时,车轮多边形引起的通过激励频率为63.7~152.8 Hz,与弹簧动刚度变化敏感区域相重合。可见,在高阶车轮多边形激励作用下,弹簧动刚度特性会较静刚度值出现剧烈变化,进而可能会导致机车垂向振动传递特性产生差异。进一步分析车轮多边形激励作用下,采用2种不同轴箱弹簧动力学模型带来的机车动力学响应差异,车轮多边形磨耗可采用如下计算进行模拟:

式中:A为多边形径跳量;R为车轮半径;β为相位差。
设置车轮多边形的阶次为18阶,径跳量为0.5 mm,采用2种弹簧模型仿真得到的构架垂向振动加速度见图7。对比图5(b)可见,在车轮多边形激扰下,机车构架振动加速度增大很多。随着运行速度的提高,构架加速度总体呈递增趋势,动刚度模型的构架加速度在80 km/h处出现突增,常刚度模型则不存在这种现象。除了在低速段差异较小外,2种弹簧模型间的构架振动加速度差异进一步扩大,且动刚度模型的仿真结果总是显著大于常刚度模型。

图7 18阶车轮多边形工况下的构架垂向振动加速度
在18阶车轮多边形激扰下,弹簧动刚度模型求得的构架加速度较常刚度模型增大百分比见图8。运行速度提高后,车轮多边形引起的激扰效应凸显,动刚度模型构架加速度较常刚度模型增幅超过27.0%,在速度为80 km/h时甚至达到61.1%。而在速度为80 km/h出现的巨大差距源于此时的车轮多边形激励频率为102 Hz,与轴箱弹簧1阶垂向固有频率吻合,进而导致弹簧动刚度相比于静刚度出现激增,使得轮轨垂向振动能量传递到构架时不能被有效缓冲和衰减。类似对于同样较为明显的23~25阶车轮多边形磨耗,机车低速运行即会激发轴箱弹簧固有频率处的动刚度效应,导致构架振动加速度相比于常刚度模型出现剧增。由此可见,当存在明显车轮多边形磨耗时,采用忽略刚度频变特性的传统常刚度轴箱弹簧建模方式会给构架振动分析带来更大误差,降低机车垂向动力学响应仿真精度。

图8 弹簧动刚度模型构架加速度较常刚度模型增大百分比
18阶车轮多边形磨耗工况下的构架振动加速度频谱见图9。轨道随机不平顺叠加车轮多边形激励后,构架垂向振动响应产生了更多高频成分。在速度为80 km/h轴箱弹簧发生内部共振时,动刚度模型的构架加速度分量在弹簧垂向固有频率处出现激增,加速度幅值超过8 m/s2,远大于此处常刚度弹簧模型的构架加速度。运行速度为90 km/h时,18阶车轮多边形激扰避开了弹簧固有振动频率,但动刚度模型的构架加速度在102、186、201 Hz附近仍存在明显峰值,这是由于弹簧在1阶垂向、2阶垂向和2阶弯曲固有频率处的动刚度突增造成的。常刚度模型则在相应频率处的加速度幅值较小,不存在峰值点。
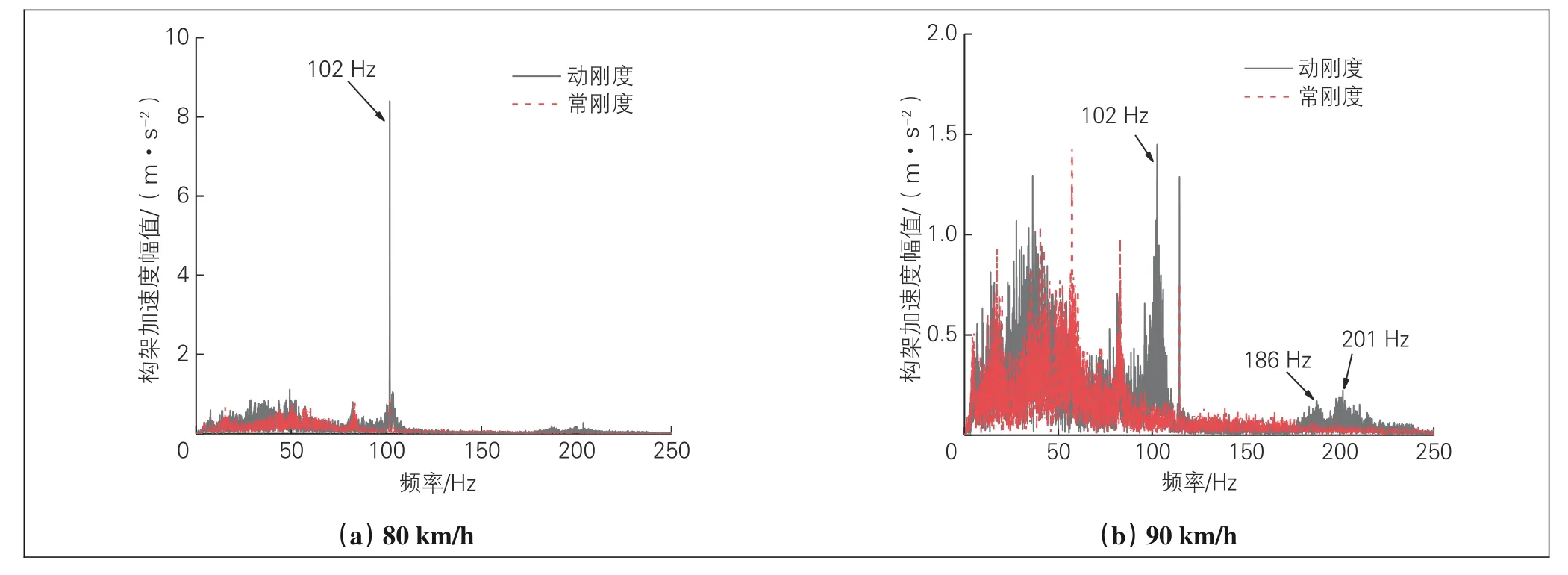
图9 18阶车轮多边形磨耗工况下的构架振动加速度频谱
2种弹簧模型对应的构架振动加速度随车轮多边形径跳量的变化见图10。可以看出,构架振动加速度随车轮多边形径跳量的增大而增大,当车轮多边形径跳量较小时,2种模型的构架加速度差异最大。
图10 构架振动加速度随多边形径跳量的变化
2种弹簧模型对应的构架振动加速度随车轮多边形阶数的变化见图11。可以看出,构架振动加速度随车轮多边形阶数的增大而增大,在阶数超过12阶后出现突增,2种弹簧模型间的构架加速度差异在车轮多边形高阶时更为明显。
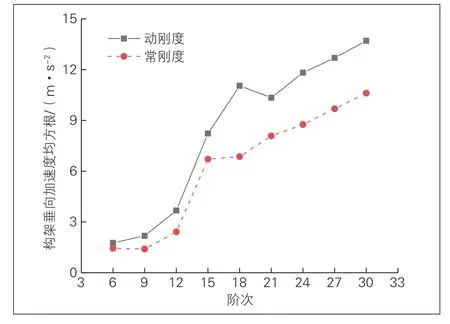
图11 构架振动加速度随车轮多边形阶次的变化
5 结论
(1)机车轴箱弹簧动刚度随激励频率的增加呈波动上升趋势,当激励频率等于弹簧安装状态的固有频率时,弹簧动刚度急剧上升,出现峰值。1阶垂向固有频率处的弹簧动刚度突增现象尤为明显,动刚度值超过50 kN/mm,远大于静刚度值1.05 kN/mm。
(2)机车动力学响应分析中,相比于传统常刚度等效力元的轴箱弹簧建模方式,考虑弹簧刚度频变特性后,对机车轴箱和车体处的振动加速度响应影响较小,对构架振动加速度影响较为明显。
(3)考虑机车存在明显高阶车轮多边形磨耗后,弹簧频变刚度模型对应的构架加速度响应总是大于常刚度模型,这是由于固有频率处弹簧动刚度突增进而导致构架加速度在相应频段出现峰值,而常刚度模型不存在这种现象。当车轮多边形激励频率接近弹簧1阶垂向固有频率时,2种模型的构架振动加速度响应差异最为显著。
