基于政府补贴的养老机构服务博弈模型
2022-07-20裴诗宇陆媛媛
裴诗宇,陆媛媛
(吉林师范大学 数学学院,吉林 四平 136000)
近年来,老年人所占人口比例日益增加,传统的家庭养老模式已经不能满足社会进步的需要,重视养老机构的开展情况成为处理社会化养老问题的努力方向.为此政府出台了多项面向养老机构的补贴政策,包括运营补贴、建设补贴、承接补贴等,但这类以机构供方为补贴对象的补贴机制逐渐出现资源配置效率差、床位空置严重等弊端,因此,对入住养老机构的老年人实施补贴成为政府的重点举措.这种“补人头”的补贴方式相较于以往,能够更直接地提高老年人入住养老机构的意愿,从而影响机构入住量.跟据老年人困难程度进行差别补贴,可合理分配财政投入、全面照顾各类情况的补贴对象.“费随人走”的补贴形式在一定程度上能减轻困难程度大老年人群体入住时的经济压力,也能使更多老年人拥有入住的机会.因此,研究“需方”补贴情形下政府与养老机构最优利润模型,对于解决社会养老问题意义重大.
目前,就各方面政府补贴问题引起了广泛关注[1-2],其中借助博弈论的相关理论进行研究的文章有很多.[3-4]郭倩[5]等研究了政府分别补贴高低服务质量养老机构问题.高晓波[6]等构建了在政府确定差别服务补贴和质量标准、养老机构在合作与非合作情形下,分别决策出最优变量的博弈模型.夏涛[7]研究了政府与养老机构在不对称信息条件下的博弈行为.Novy-Marx[8]引入风险分担因素,研究在不同条件下政府对养老服务项目补贴的影响.研究对养老服务需方补贴的文章也不少.马骁[9]综合分析了国内研究成果,提出机构养老服务补贴模式应转向“需方”补贴的建议.张翔[10]等通过实地调研,构想了对于养老服务“需方”补贴的具体政策.董红亚[11]通过对浙江省养老服务补贴政策的分析,强调“补人头”方式的现实重要性,并为进一步完善补贴制度提出了一些建议.赵鹏程[12]等分析了非中心城市的养老困境.张荣燕[13]等分析了传统机构养老补贴的不足,提出包括机构养老需方补贴覆盖对象、补贴方式、补贴标准等在内的具体补贴内容.以上有关政府与养老机构博弈行为的文章都是以补贴养老机构“供方”为背景,而对于养老机构“需方”补贴只存在建议和重要性分析,未涉及政府在补贴养老机构“需方”情形下与养老机构的博弈问题.本文在政府对入住养老机构的老年人实施补贴的背景下,建立政府与养老机构的二阶段博弈模型,采用逆向归纳法求解养老机构和政府的最优决策问题,并计算双方最优利润函数,为政府解决养老问题提供借鉴.
1 模型的建立
1.1 符号说明
本文涉及到的变量符号有:t0表示政府对入住养老机构老年人的基准补贴,p表示养老机构的收费价格,x表示养老机构服务水平,a表示市场需求对机构收费价格的弹性因子,b表示市场需求对机构服务水平的弹性因子,g表示老年人的困难程度,γ表示基准补贴对困难程度的弹性因子0≤γ≤1,β表示养老机构投入成本对困难程度的弹性因子0≤β≤1,D0表示市场基本需求量,c0表示养老机构单位服务的边际成本,k表示养老机构提高服务水平的成本系数,D表示养老机构的市场需求量,π(p,x),W(t)分别表示养老机构利润函数和政府福利函数.
1.2 模型假设
(1)困难程度是指包括失能水平、失智水平、家庭情况(低保家庭、低收入家庭、计划生育特殊家庭)、残疾程度等在内的能够评定补贴标准的各种因素.
(2)老年人的入住补贴是指在老年人入住养老机构后,跟据其困难程度申请对应的补贴金,补贴直接下发给老人,即可理解为免除了老年人入住机构的部分费用.由文献[4]假设养老机构市场需求函数为:
D=D0-a(p-t0gγ)+bx.
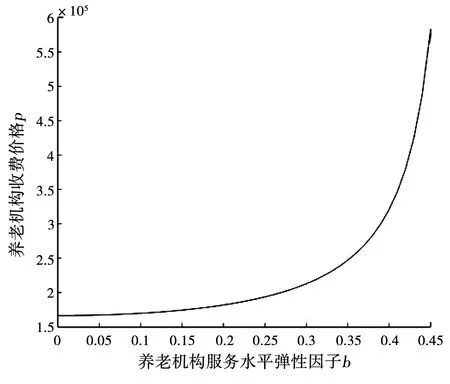
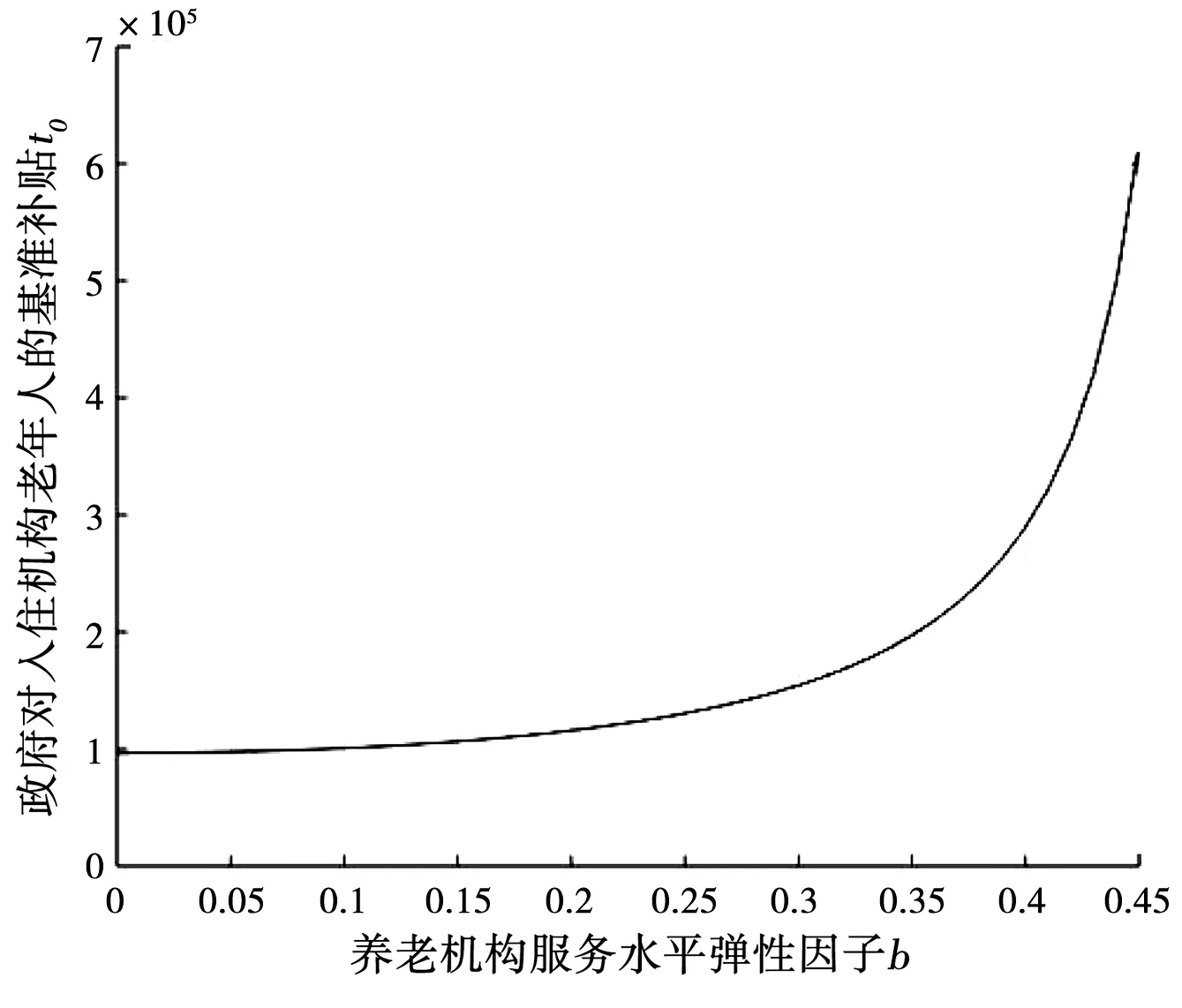
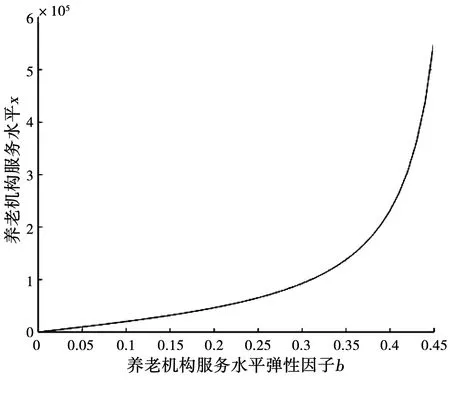
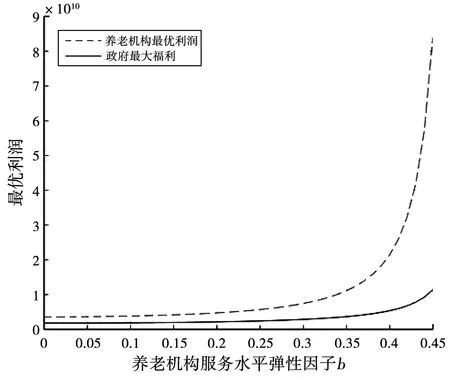
即养老机构市场需求量与机构定价成反比,与机构服务水平及政府补贴成正比,要求满足D0-ac0gβ>0.其中,t0gγ表示在政府基准补贴金额t0下,入住机构的老年人根据其困难程度g最终所申获的实际补贴金额.在实际生活中,补贴存在上限,从而规定0 根据假设得到政府福利函数和养老机构利润函数. 政府福利函数: 养老机构利润函数: 跟据Stackelberg博弈模型的逆向求解原理,先分析养老机构最大利润的优化模型 定理1当系统参数满足b2-ak<0,可得到最优服务价格及最优服务质量分别为: 证明将π(p,x)分别对p,x求偏导,有 解得驻点为 因π(p,x)的Hessian矩阵为 所以,π(p,x)是关于p和x的凹函数,即养老机构收费价格及服务水平在驻点处取最大值.同时,容易验证x>0,p>0. 证毕. 性质1养老机构的影响因素分析. 由上述分析可知,政府增加基准补贴金额,会提高老年人入住养老机构的意愿,使养老机构市场需求量变大,而机构为了自身利益最大化会努力提升服务水平,从而使机构收费价格变高. 定理2政府以社会福利最大化为目标,在参数满足定理1的条件时,确定出对老人的最优基准补贴价格为: 即 又有 证毕. 故在此模型下,养老机构的最大利润为: 政府的最大福利为: 性质2参数对最优决策的影响分析. 可知养老机构最优定价与养老机构服务水平对市场需求影响程度b呈正相关,与养老机构收费价格对市场需求影响程度a呈负相关. <0. 可知政府对入住机构老年人的基准补贴与机构服务水平弹性因子b呈正相关,与机构收费价格的弹性因子a呈负相关. <0. 可知养老机构最优利润与机构服务水平弹性因子b呈正相关,与机构服务价格的弹性因子a呈负相关. <0. 可知政府最大福利与机构 服务水平弹性因子b呈正相关,与机构价格的弹性因子a呈负相关. <0. 可知养老机构最优服务水平、机构最优定价、政府最优基准补贴、政府及养老机构最优利润均与老年人困难程度g呈负相关. 目前,机构养老是国家大力支持的养老模式之一.以北京市东城区康馨园养老院为例,该机构收住的老年人可依据北京市委颁布的有关困境老年人入住养老机构的补贴政策,按照符合自身条件的补贴标准申请对应金额的入住补贴,用于免除部分机构入住费用.假设市场基本需求量为D0=10(万人),养老机构年投入成本为c0=10(万元),满足条件的参数为:k=0.4,a=0.6,b=0.4,g=0.64,γ=0.5,β=0.25,计算结果见表1. 表1 算例最优结果 当系统参数满足所设范围时,得出以下结论: (1)随着养老机构服务水平弹性因子b的增大,养老机构最优定价p*呈上升趋势,即最优定价逐渐增高,反之最优定价逐渐降低(图1). 图1 养老机构服务水平弹性因子对养老机构收费价格的影响 图2 养老机构服务水平弹性因子对政府对入住机构老年人价格补贴的影响 (3)随着养老机构服务水平弹性因子b的增大,机构服务水平x*呈上升趋势,即养老机构服务水平逐渐提高,反之服务水平逐渐降低(图3). 图3 养老机构服务水平弹性因子对养老机构服务水平的影响 (4)随着养老机构服务水平弹性因子b的增大,养老机构最优利润和政府最大福利均呈增加趋势,但养老机构最优利润始终大于政府最大福利(图4). 图4 养老机构服务水平弹性因子对最优利润的影响 本文在政府对养老机构“需方”补贴的情形下,建立了政府和养老机构的Stackelberg主从博弈模型,以双方利润最大化为目标进行了最优化求解.政府受老年人困难程度等因素影响,以社会福利最大化为目标制定补贴政策,通过决策老年人入住养老机构的基准补贴金额起到调控养老机构市场的作用,机构跟据补贴内容,在一定情况下选择提高服务水平和价格,能够增加社会效益和养老机构收益.政府针对“需方”补贴将扩大老年人接受入住养老机构理念的影响力,减轻一部分困境老人的家庭负担,符合解决养老问题和推动我国养老服务产业发展的需求,为政府对养老机构“需方”补贴政策提供研究思路和理论支持.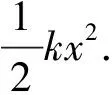
1.3 建立模型
2 模型的求解
2.1 养老机构最大利润模型
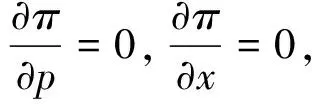
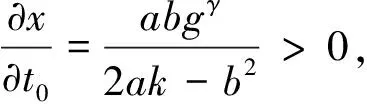
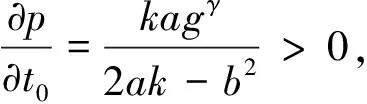
2.2 政府最大福利模型
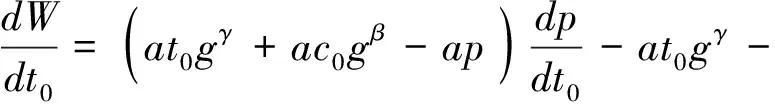
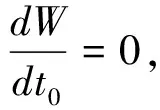
2.3 系统最优决策
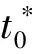
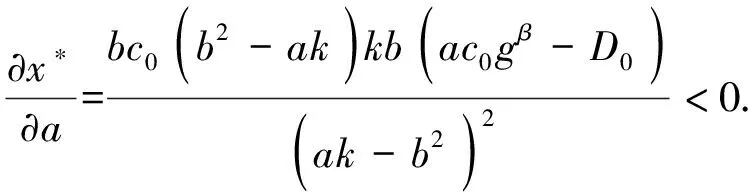
3 算例分析
3.1 算例结果
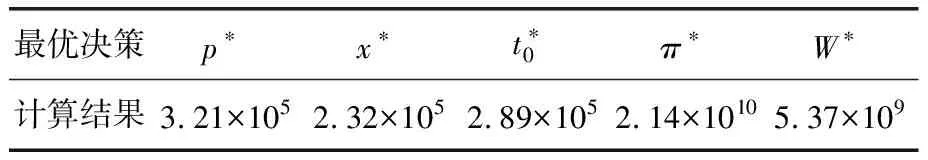
3.2 养老机构服务水平弹性因子分析
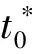
4 结语
