考虑空隙影响的岩石统计损伤模型研究

2022-07-20李越梅吕洪淼刘文博晏祥智

煤炭科学技术 2022年5期

李越梅，吕洪淼,，刘文博，晏祥智

(1.辽东学院城市建设学院，辽宁丹东 118003；2.辽宁工程技术大学土木工程学院，辽宁阜新 123000；3.云南省房地产开发经营(集团)有限公司，云南昆明 650000)

0 引言

为更好地描述材料的应力-应变特性，国外学者在20世纪初提出“损伤”理论，认为相对于理想材料而言，现有的材料在未加载前自身就具有损伤，即力学性质就已经发生了劣化。因此，通过构建一套完整的损伤力学理论，进而建立了可以描述材料变形性能的方程。随着损伤理论不断发展和完善，岩石领域的专家将该理论引入到岩石力学中，结合现有经典的力学理论逐渐形成了宏观、细观和准宏观的损伤力学[1]。上述理论发展至今，最核心的思想就是如何构建一个满足试验条件的损伤变量，并结合有效应力原理将其引入到力学本构模型中，进而来通过参数反演得到最终的模型方程，使得该方程可以较好地描述岩石在荷载作用下的应力-应变关系。近些年，学者们发现了岩石在加载过程中产生的裂隙等缺陷都是随机的，没有规律可循[2-3]。因此，结合概率统计理论和损伤力学理论，将概率分布函数引入到构建的损伤变量中，通过建立统计损伤模型来研究岩石在荷载作用下的破坏机理和损伤演化规律。

根据上述对损伤理论的介绍，现通过国内外学者的研究成果，来说明岩石统计损伤理论的发展现状。其中，徐卫亚等[4]将岩石的变形分为了塑性应变和弹塑性应变，结合试验数据和损伤理论建立了考虑弹塑性统计模型。LAI等[5]通过开展围压对岩石软化特性影响的试验，建立考虑应变软化对损伤影响的统计模型。LI等[6]为了使得现有屈服函数可以描述三向受力作用冻土的屈服特性，采用统计损伤原理将传统Mohr-Coulomb准则进行了改进，并构建了统计冻土损伤模型。曹文贵等[7]认为岩石只是有空隙缺陷和岩石颗粒骨架两部分组成，在考虑空隙变形的基础上，引入了反应空隙压缩变形的变量，进而建立非线性统计损伤模型。

上述研究成果对岩石孔隙的关注较少，且构建的本构模型较为复杂、模型中的未知参数较多，使得模型不容易求解。因此，笔者通过引入空隙损伤影响系数，结合损伤力学来描述岩石在加载过程中真实损伤状态。对围岩进行常规三轴压缩试验，研究砂岩在不同条件下变形强度特性以及损伤演化规律，以此提出考虑岩石空隙损伤的统计损伤本构模型。

1 试验三轴力学试验

采用的砂岩均取自阜新恒大煤矿1号矿井。开展三轴力学特性试验的设备如图1所示，岩石试验系统的型号为TAW-2000。该岩石试样的外观呈灰色，表面无明显的裂隙和层理等缺陷，尺寸和大小严格按照岩石力学协会制定的规则制备。开展三轴力学特性试验步骤：① 采用位移控制方式，以0.002 mm/s的速率将围压加载到预定值，在此过程中需要一直保持围压值不变。② 以同等的速率加载轴压至岩石发生破坏后，持续增加轴向应变直至得到岩石的残余应变变形。③ 先卸载轴压后卸载围压后，以时间间隔保存数据。④ 按照地应力的围压分别选取0、10、20和30 MPa。

图1 TAW-2000岩石三轴试验机Fig.1 TAW-2000 rock three triaxial test machine

图2 砂岩岩样Fig.2 Sandstone rock sample

根据上述步骤开展试验，绘制出试验曲线如图3所示。由图3可知，在同一围压作用下，应力-应变曲线都是随着应变增大，应力的变化规律呈现出先增大再减小趋于稳定，而峰值强度随着围压增大而增大，也说明了围压对于提升岩石的力学特性有显著的帮助。

图3 试验结果Fig.3 Test results

2 统计损伤本构模型建立

经过几十年的发展，岩石损伤理论已经有了完善的体系，学者们一直认为岩石在荷载作用下产生的损伤实质上是岩石自身损伤以及变形过程中的弹性损伤和黏塑性损伤叠加而成的。尤其是岩石内部微裂纹的随机分布特性和后期岩石损伤演化规律，都与岩石自身初始损伤有关联[8]。因此，可以假设岩石的应变满足以下关系[9]为

(1)

式中：m、F为分布常数；ε为应变；P(ε)为概率密度函数。

假设在某一级荷载作用下，在某一时间岩石内部已破坏的微元体数目为Nt，岩石内部总微元的数目N，两者之比可以定义为损伤变量D[10]，即：

D=Nt/N

(2)

式中：Nt为在某一级荷载作用下，在某一时间岩石内部已破坏的微元体数目；N为岩石内部总微元的数目；D为损伤变量。

岩石内部已破坏的微元体数目Nt为

(3)

得到

(4)

(5)

式中，σi为应力；σi*为有效应力。

三轴压缩状态下岩石应力-应变关系满足[11]：

σ1=Eε1(1-δD)+μ(σ2+σ3)δD

(6)

其中，δ为变化系数；μ为泊松比；E为弹性模量。为进一步描述岩石内部空隙对岩石应力-应变关系的影响，现用空隙损伤影响系数f代替变化系数δ，可得

σ1=Eε1(1-fD)+μ(σ2+σ3)fD

(7)

式中，f为空隙损伤影响系数。

通过联立式(2)—式(7)得出：

(8)

对于分布常数m，F0一般通过建立关于分布常数表达式来确定[12-13]。由图4可知，存在以下几何关系：①ε1=ε1c时，有σ1=σ1c；②ε1=ε1c时，有∂σ/∂ε=0。其中，ε1c为峰值点应变；σ1c为峰值点应力。

图4 岩石应力-应变曲线Fig.4 Rock stress and strain curve

由条件②可知，

(9)

由条件①可知，

(10)

将式(9)进行展开得到

(11)

将式(10)和(11)联立得：

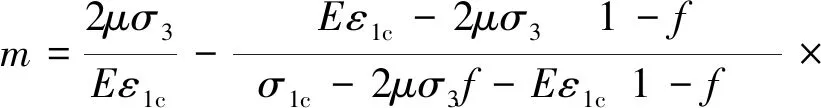
(12)

(13)

式(12)和式(13)中确定出分布常数m和F，但是表达式中还含有未知参数f需要确定。

当变形进入残余变形阶段后，岩石属于完全变形破坏状态，此时岩石产生的变形为岩石塑性不可逆变形，即假设在残余应变阶段，岩石损伤变量为D=1[14]，且应力-应变曲线上残余点的残余应力表示为σr，残余应变表示为εr，得出

(14)

式中：σr为残余应力；εr为残余应变。

弹性模量E计算[15-17]如下

(15)

式中，B为径向应变与轴向应变的比值。

由文献[18-19]可知，峰值应力和峰值应变之间存在以下关系：

(16)

ε1c=aσ3+b

(17)

式中：a、b均为常数；c为黏聚力；φ为内摩擦角。

将式(16)和式(17)代入参数确定方程中即可得到任意围压作用下参数值。将该参数值代入式(7)中，得到满足任意条件的统计损伤本构模型。

3 统计损伤模型验证

将式(7)改进的统计损伤模型方程代入到软件Origin中[20]，绘制出不同围压的模型曲线。根据上述参数确定方法确定出模型参数见表1。

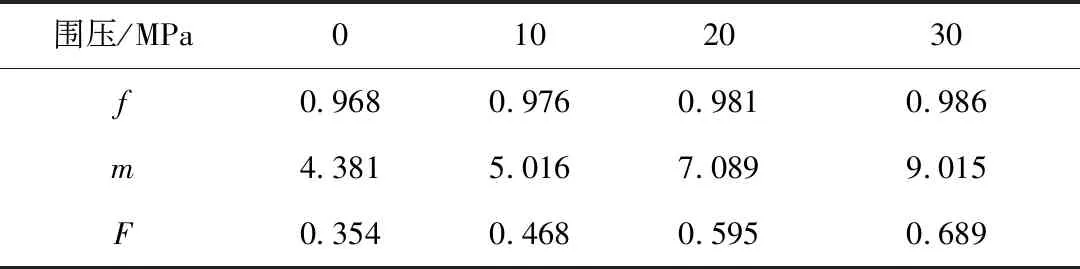
表1 改进统计损伤模型的参数Table 1 Parameters of the improved statistical damage model

表1中的参数具有局限性，它们都是在围压为0、10、20、30 MPa的特定条件下确定的，无法将其推广至其他围压条件下进行应用，故需要寻找参数值与围压之间的关系。采用指数函数对试验数据进行拟合如图5所示。

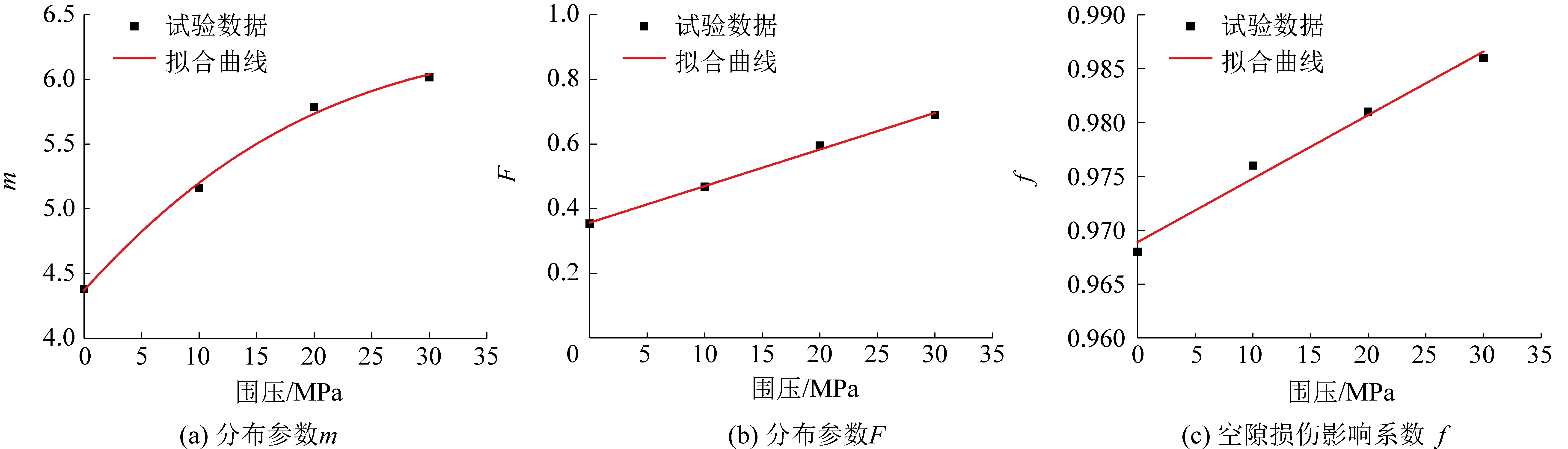
图5 分布参数与围压关系Fig.5 Distribution parameters and confining pressure relationship

由图5可知，参数值与围压之间具有较好的吻合度，且R2均大于0.95。

m=-2.192exp(-σ3/20.786)+6.562

(18)

F=0.357+0.011σ3

(19)

f=0.969+5.900×10-4σ3

(20)

根据所建立的损伤统计模型方程，把不同围压三轴压缩试验曲线反演所获得的参数，代入损伤方程中，绘制试验和拟合对比曲线如图6所示。

由图6可知，建立的模型所绘制出的曲线和试验曲线变化规律较为一致，这说明了引入空隙损伤影响系数，构建出新型损伤模型可以较好地描述损伤演化。相对文献[7]而言，该统计损伤模型更加简单，模型中的参数较少、参数的计算公式相对简单，且也达到了描述变形特性的效果较好。再将上述参数值代入式(7)中，得到损伤演化规律如图7所示。

图6 拟合曲线与试验曲线Fig.6 Fitting and experimental curve

由图7可知，岩石在同一围压作用下的损伤变量的变化规律都是呈现出先增大后趋于稳定的趋势，这是由于岩石在荷载作用下内部原生裂隙会进一步发展、扩散，直至贯通为宏观裂缝，导致岩石发生变形破坏，后续试验岩石试样沿着破裂面滑移，最终使得岩石的损伤程度逐渐加剧。但是在损伤变量变化初期曲线重合度较高，这是因为岩石内部空隙处于压缩变形状态，此时新生的裂隙等缺陷较少；加载中期损伤变量变化曲线逐渐分离，这是由于空隙压密后岩石内部裂隙开始大量的新生和发育，使得岩石损伤加剧；在加载后期，岩石内部贯通裂缝基本形成，损伤变量的变化规律趋于稳定，微裂纹在较为软弱的区域汇聚，使得损伤速率进一步提高且趋近于1。此过程与实际岩石的破坏损伤演化基本一致，说明了建立损伤演化模型的合理性与正确性。

图7 损伤演化规律Fig.7 Damage evolution

综上所述，建立的统计损伤模型可较好地反应岩石的变形特性，也可较为真实反映巷道围岩的变形情况，对实际工程中巷道围岩-支护体的设计具有指导意义，但是实际工程中围岩所受的三向应力大小各不相同，鉴于试验条件约束无法实现，故需要在以后研究中对岩石做真三轴试验，才能更好地反映实际地层开挖后围岩的受力、变形情况。