基于NSGA-III的跨声速转子弯掠组合MOO设计
2022-07-20李博文
李博文,吴 虎
(西北工业大学动力与能源学院,陕西 西安 710072)
1 引言
自从弯掠叶型被提出以来,一直作为叶轮机械设计领域的热点,受到了众多学者广泛究。Denton采用数值模拟技术研究了弯掠对转子的性能影响,发现弯掠转子在设计工况下性能提升较小,但是稳定工作裕度能够得到明显提升,并且能够改善非设计工况下的流通能力。Widia等分别对单级和多级压气机进行研究表明,叶片前掠可以削弱叶尖处激波、附面层以及泄露流相互干扰所带来的影响,从而提高压气机的工作裕度,Gallimore将弯掠设计引入多级压气机三维设计中,也取得了一定的效果。中国学者季路成对某跨声速压气机叶片进行弯掠设计后,总结出弯掠叶片通过对流体施加径向叶片力来改变各基元级的工况,从而影响压气机的总体性能,茅晓晨等对某单级压气机进行弯掠设计,研究发现,弯掠叶型能够明显地改善叶尖和叶根附近的流动,并降低二次流的影响范围。
以上研究中,叶片弯掠改型,多依赖于研究者的工程经验。近年来计算机技术和人工智能发展迅速,代理模型技术和进化算法在发展中日益成熟,越来越多的学者将二者与叶轮机械的优化相互结合,以计算智能来减小设计者经验对于结果的影响。同样有研究者将此技术结合应用于弯掠叶型设计的领域,Seo利用响应面模型对某型风扇进行弯掠优化设计,使其效率提升了1.75%,Jang同样采用响应面模型对某跨音速压气机设计,通过对叶片弯掠的控制使其角区流动得到改善以及降低了叶尖损失,从而提升了压气机的性能,哈工大学者王祥锋、韩万金结合响应面模型和遗传算法对Rotor67转子进行了弯掠优化设计,使其总压比提升了约1%。
综合前人的研究可以发现,将代理模型与智能算法结合应用在弯掠设计上的研究并不丰富,早期大多数的研究手段是基于响应面模型的优化,而响应面模型作为一种线性近似模型,在应对CFD计算所得出复杂数据时映射能力并不理想;同时优化算法的选取也较为单一,多为单目标优化算法。而近年来数值优化算法发展迅速,多目标遗传算法已成为越来越多的研究者所关注的方向。
考虑到上述两个方面的因素,本文采用Rotor67跨声速转子作为研究对象,使用非线性代理模型BP神经网络作为近似映射,选取近峰值效率点的绝热效率、压比、流量三个性能参数作为优化目标,采用多目标搜索能力更强的NSGA-III遗传算法实施多目标优化;同时为了减少训练所需样本数,采取了将优化结果和神经网络样本库相互迭代的训练策略;并对NSGA-III与NSGA-II的结果进行对比分析,得到了最终的设计叶型。
2 计算算例和数值方法
本文研究对象为NASA Lewis研究中心设计并试验NASA Rotor67转子,其主要设计参数如表1所示。

表1 Rotor67设计参数
本文利用NUMECA软件AUTOBLADE模块对叶片进行参数化造型,沿径向选取14个截面,每个截面的吸力面和压力面各采用包含30个控制点的贝塞尔曲线对叶片进行拟合。通过控制叶片轴向和周向积叠线的方式来控制叶片的弯掠规律,选取重心为叶片积叠点,轴向和周向积叠线均采用包含4个控制点的贝塞尔曲线进行拟合。
网格划分使用Ansys Turbogrid模块,计算采用单通道网格,网格无关性验证如表2所示,网格数量由30万增长至80万,计算得到流量、总压比、绝热效率呈逐渐增大趋势,当网格量大于70万时流量、总压比、绝热效率变化趋于稳定,综合考虑了求解准确度和求解时长,认为单通道网格数量控制在70万至80万之间最为合适,Rotor67划分的计算网格如图1所示。采用CFX为求解器进行仿真计算,湍流模型采用 双方程湍流模型,为满足 湍流模型对于 要求,第一层网格高度为5e-5m,工质为理想空气,壁面为绝热壁面。边界条件为进口总温、总压及进口气流角,出口背压条件为平均静压。
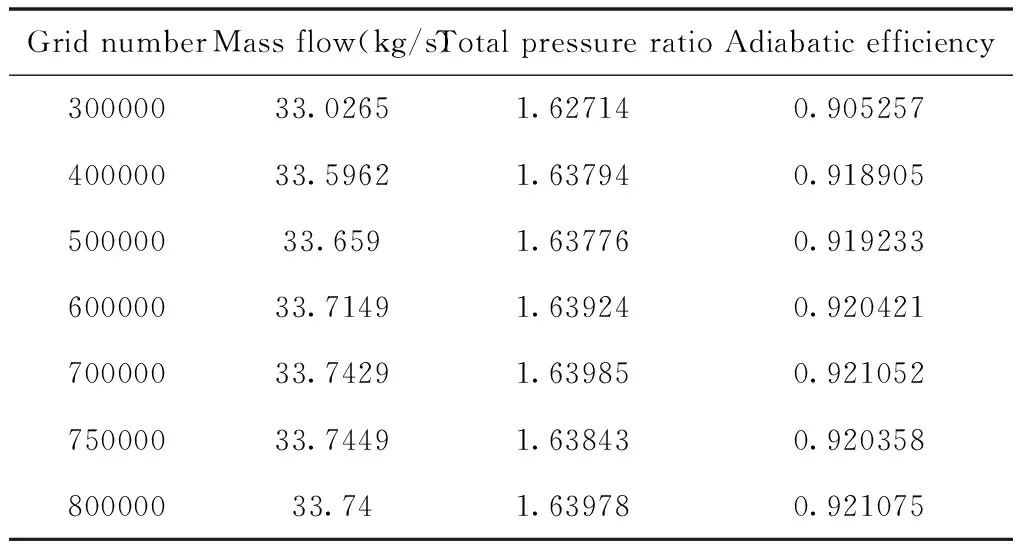
表2 网格无关性验证

图1 Rotor67计算网格
采用上述网格和求解设置对研究对象进行了算例验证,得到CFD仿真结果的堵点流量为34.6kg/s,实验测得的堵点流量为34.9kg/s,误差约为0.9%,图2给出了设计转速下拟合叶型的CFD仿真结果与实验结果的对比,从效率特性和压比特性的对比图可以看出,绝热效率的CFD仿真结果与实验值吻合良好,而压比整体上相比于试验值偏低,分析原因这可能是由于经过AUTOBLADE拟合所得到的叶片与实验用叶型存在细微差别,以及数值计算方法和湍流模型等原因所致。
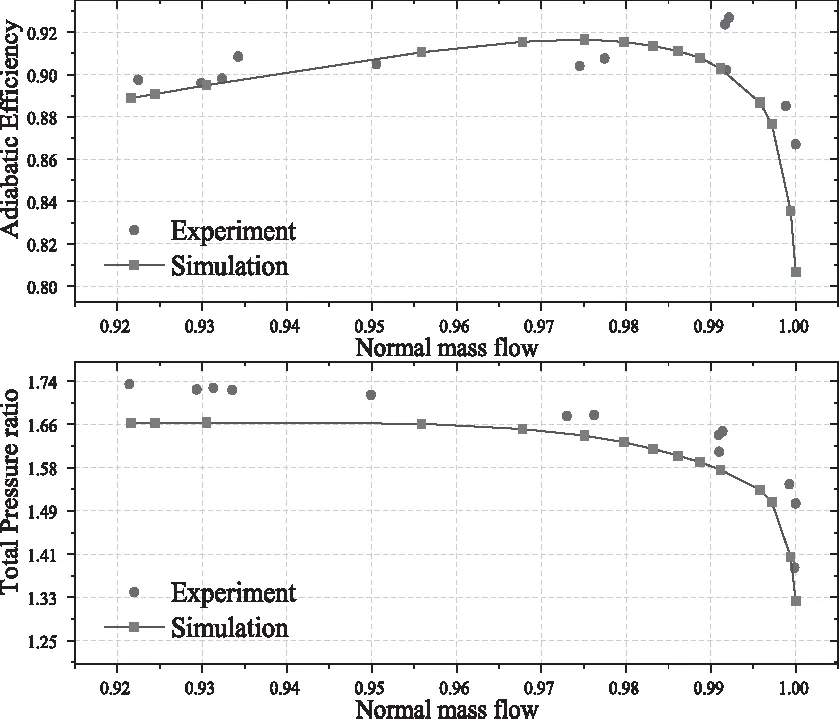
图2 Rotor67效率压比特性图
图3给出了近峰值效率工况下,周向平均总压比和出口绝对气流角沿展向的分布。可以看出计算所得总压比和气流角分布与实验值吻合良好,表明明本文拟合所的而出的的叶型以及所采用的数值计算方法是可靠的。
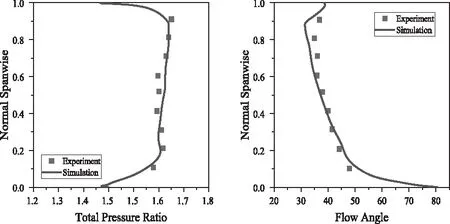
图3 近峰值效率点周向平均总压比和气流角展向分布
3 叶片弯掠的参数化控制
本文通过对积叠线控制点坐标参数化来实现对叶片弯掠的控制。图4给出了周向积叠线和轴向积叠线示意图。图中控制点由轮毂到机匣均匀分布,文中选取所有控制点所对应的横坐标值作为控制参数分别记作s
、s
、s
、s
和l
、l
、l
、l
。
图4 叶片积叠线贝塞尔曲线控制点
4 BP神经网络的建立
4.1 样本库的建立
为了建立构建神经网络模型的样本库,需要在样本空间上进行均匀的采样,在本次研究中采用了拉丁超立方的采样方式对样本空间(积叠线上8个控制点)进行了随机100组抽样。在该过程中,利用Isight软件,将AUTOBLADE叶片参数化造型、Turbogrid网格生成、CFX流场求解以及CFD-POST后处理过程进行集成,实现了样本库的自动化建立。
4.2 神经网络的构建
4.2.1 数据预处理
在进行神经网络回归之前,需要对样本库中数据进行标准化处理,这是因为数据取值范围不同,而神经网络训练过程中所采用的是梯度下降算法,使所有变量映射到同一区间能够有效的提升模型的收敛速度,研究中所采用的数据归一化方法为0-1标准化,即对原始数据进行线性变换使其取值范围缩放至[0,1]区间,式(1)给出了0-1标准化的计算公式
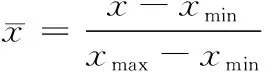
(1)
4.2.2 激活函数和过拟合的防止
由于样本数据较为复杂,实践表明,仅使用单层神经网络并不能有效地构建拟合效果良好的神经网络。为了使神经网络模型能够较好的贴合训练样本,本文自主编程构建多层神经网络,并对模型进行反复的测试。最终测试发现包含三层隐藏层的神经网络,每层神经元50个即可使得样本的均方根误差为10数量级。同时考虑到,当隐藏层数大于1时,由于梯度下降算法是基于导数的,且通常所使用的激活函数sigmoid函数在上一层输入值绝对值极大的情况下其导数接近于0,导致梯度下降算法无法继续进行。故经多次的调整和测试,本文最终所采用的神经网络激活函数选取了Leaky Relu函数,如图5所示。

图5 激活函数图像及表达式
由于研究采用多隐藏层神经网络,在验证测试集时发现容易出现过拟合的现象(即模型在样本数据上表现良好,在测试数据上表现反而极差的现象),因而导致模型的泛化能力下降,为了防止该现象的发生,故在此选用L2正则化的方式进行防过拟合处理,即将原有的均方误差函数变为式(2),式中括号内的第一项是均方和(即正则化之前的误差项),第二项为正则化项,用来控制均方差使其不至于过小导致过拟合现象出现,其中λ为正则化系数。本文中最终调试神经网络λ取值为10时,神经网络能够达到良好的拟合效果。
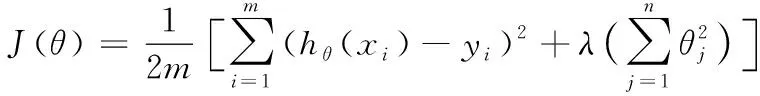
(2)
4.2.3 神经网络的训练以及测试策略
为了确保所建立的神经网络能够准确地拟合样本数据,本文将样本库中的数据随机抽取出30组作为测试集,剩余的样本作为训练集进行神经网络的训练,利用测试集测试得到的神经网络,若不满足误差则重新分组,修改神经网络结构、参数重新训练,直至测试样本误差在0.1%以内。该过程流程图7所示。
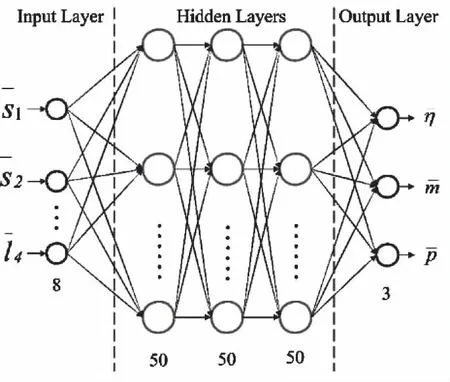
图6 神经网络结构图
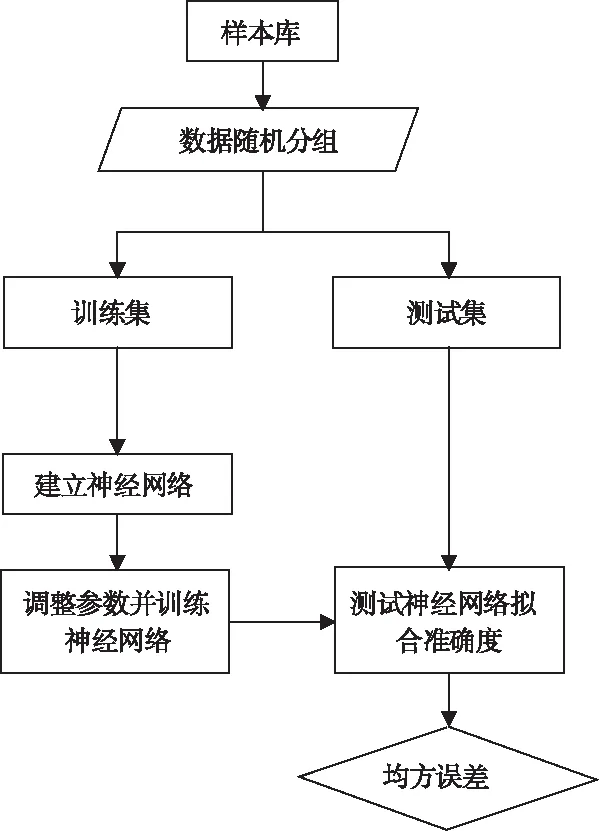
图7 神经网络训练流程图
经过上述方式调整神经网络,最终得到的神经网络测试集的测试结果如图8所示。其中绝热效率、压比、流量的决定系数R分别为0.899、0.974、0.975。由可认为本文所构建的BP神经网络模型拟合效果良好。
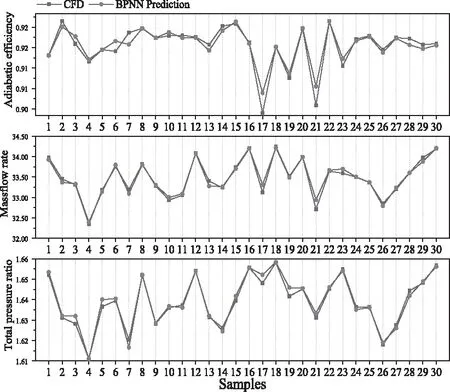
图8 神经网络测试效果图
5 NSGA-III遗传算法的建立
5.1 算法简介
研究所采用的多目标遗传算法为Kalyanmoy Deb等人于2013年所提出的NSGA-III遗传算法,该算法在NSGA-II算法的基础之上提出了参考点的概念,提高了算法的收敛性以及最优解分布的均匀性,相比于NSGA-II使用拥挤度的方法,NSGA-III采用参考点的方式能够有效的提高解的多样性,研究发现,在求解三个及以上目标的问题中,NSGA-III算法具有明显的优势,图9给出了NSGA-III算法的流程图。
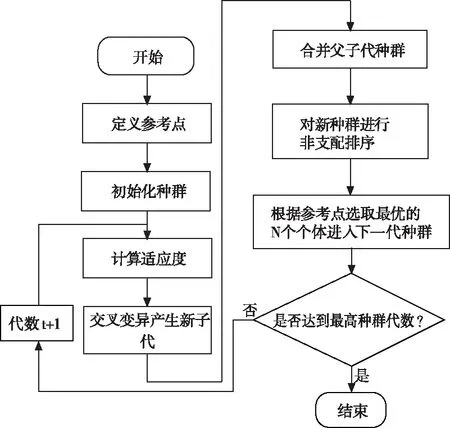
图9 NSGA-III算法流程图
5.2 样本库的局部加密策略
为了保证研究中所抽取样本在空间分布均匀,前文中采用了拉丁超立方的抽样方式,在初次抽样过程中,仅抽取了100组数据,研究结果表明,在该样本数量下所建立的神经网络模型在全局上具有良好的拟合效果,而在局部并不一定能够很好的拟合CFD计算数据,这就导致了在最优解附近神经网络模型具有较大误差。
为了提高最优解处BP神经网络模型的精度,在研究中采用了遗传算法和神经网络交替训练的方式,即采用少量初始种群的遗传算法计算出前沿最优解,并将其加入样本库中重新进行训练,通过此方式来增加在最优前沿处的样本数量,经过多次迭代,直至达到前沿解的神经网络预测结果与其CFD数值验证的误差满足精度需求。该过程流程如图10所示。最终计算结果表明,本文所采用的算例经过三次迭代,即可以满足误差需求,最终训练样本为160组。
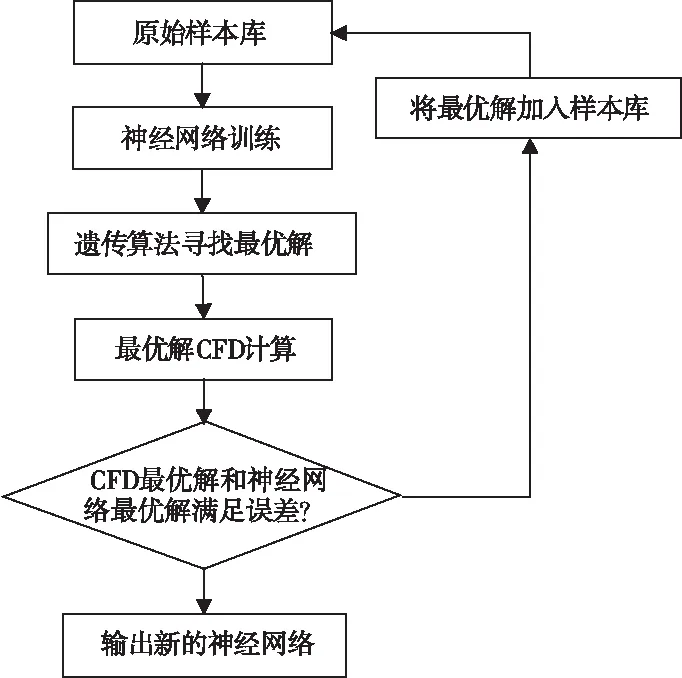
图10 样本库局部加密方案流程图
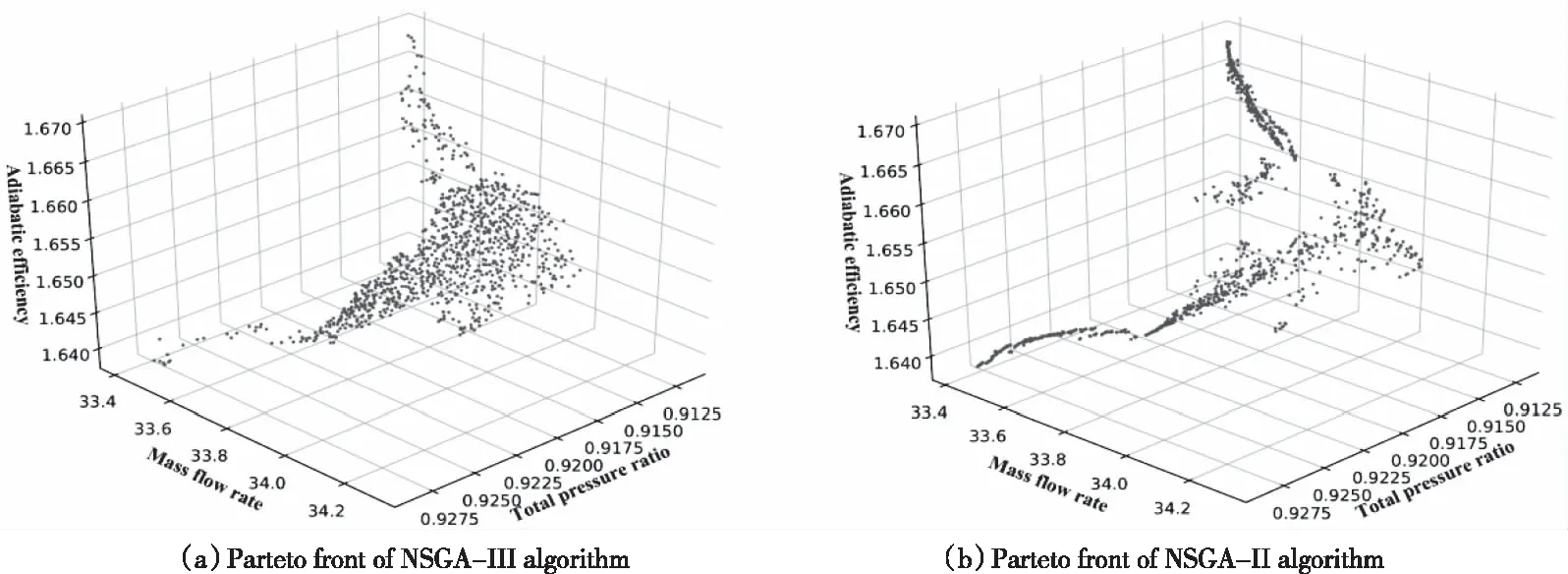
图11 两种遗传算法Pareto前沿对比
5.3 优化结果
5.3.1 优化目标
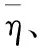

(3)
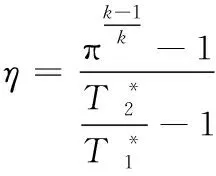
(4)

(5)
5.3.2 优化结果
本文优化的目标为标准化绝热效率、压比、流量,使三个目标均达到最大值,在进行最优解局部加密时设置种群数量为30,最大代数为2000,交叉概率为0.9,变异概率为0.1。经过三次迭代加密以后,验证最优解附近的决定系数R均达到0.9以上。对最终得到的神经网络,分别采取了NSGA-II和NSGA-III进行寻优,为了得到尽可能多的Pareto前沿以研究两种算法之间的差异,两种算法所设置的种群数量为均为1000,最大的代数为均为2000代。
经过遗传算法寻优,分别得到了两种算法对应的1000组非支配最优解,图11(a)为经过NSGA-III算法所的到的最优解分布,图11(b)为经过NSGA-II算法所得最优解的分布,可以观察到NSGA-III的pareto前沿呈现曲面状分布,且分布均匀,NSGA-II的pareto前沿呈现条状分布,且分布局部集中在边界区域,这意味着经过NSGA-II优化产生了大量单个目标占优的个体,这对三个及以上目标的寻优极为不利。而在最优解的中间区域,前者分布均匀,后者解集几乎却没有覆盖该部分,这说明NSGA-II算法并不能够有效地寻找出三个目标均占优的个体。综合上可以认为在本算例中NSGA-III的性能远优于NGGA-II。
由于优化变量数量有8个,并不利于可视化,本文对NSGA-III和NSGA-II优化所得到的优化变量组合分别应用PCA技术进行降维处理,将其维度降低至三维,并绘制出对应的散点图,如图12所示。图中可以观察到,NSGA-III优化所得到的优化变量在空间分布集中且连续;而NSGA-II优化所得到的设计变量在空间上的分布则较为离散;从最终最优解变量选择的角度来说,NSGA-III具有更高的稳定性。
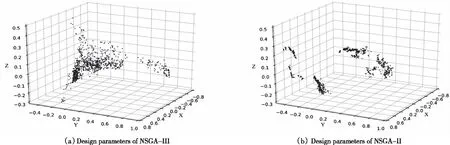
图12 两种遗传算法设计变量分布
本文从1000组最优解提取出效率大于92.5%、流量大于33.95、压比大于1.65的个体共计30个,在解集中选取效率最大一组解作为最终的优化结果。其相关参数如图12所示。从优化结果上来看,在近峰值效率点处的优化效果良好,绝热效率、压比、流量分别提高了0.646%、0.873%、0.513%。同时发现BP神经网络所预测的性能与CFD计算所得性能之间的误差分别为0.004%、0.1%、0.1%,充分证明了本文所采用的神经网络预测模型具有良好的准确性。

表3 优化参数对比
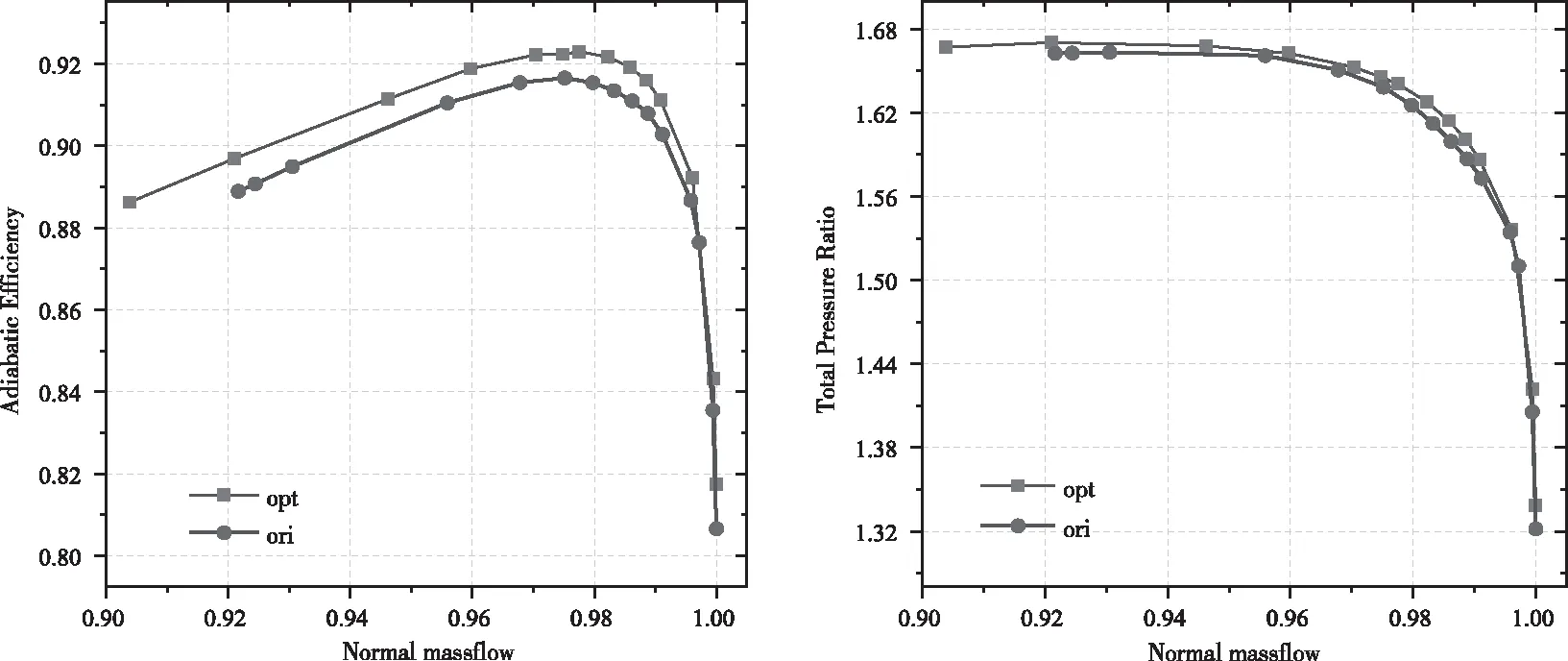
图13 优化前后效率压比变工况对比
研究结果发现,经过优化改型后的转子除了在近峰值效率点的性能得到了提高,其堵塞点流量也得到了一定提升,由原型的34.6kg/s提升至34.95kg/s,相对原始叶型提高了超过一个百分点。图11给出了优化前后压比和效率特性的对比。可以看出,经过优化后的叶型在失速点的绝热效率、压比也得到了提高,绝热效率提升约为0.9%,压比提升约为0.43%,同时其工作裕度也得到了拓宽,改型优化结果表明,弯掠Rotor67转子的气动性能得到了全方位的提升。
6 流场分析
前文的研究结果表明在经过本文的优化设计,研究对象在近峰值效率点的气动性能有了较大的提高。图14给出了在近峰值效率点优化前、后绝热效率、压比的展向分布,图中可以看出优化后的叶型在全叶高范围内,效率、压比总体上均有小幅提升,但是大约在10%~20%和75%~90%叶高处的效率相比原始叶型较低,在50%叶高附近优化叶型的压比要略低于原始叶型。
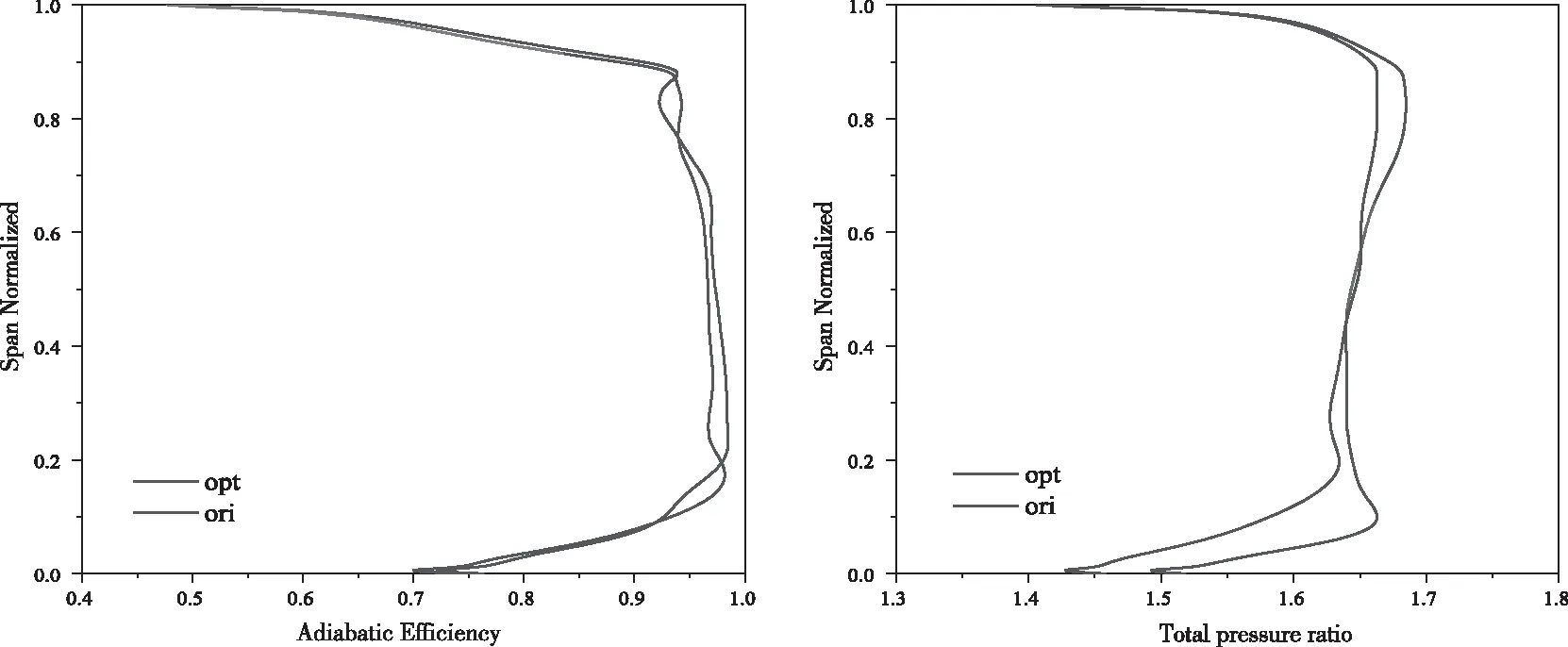
图14 优化前后效率压比展向分布
图15给出了在峰值效率点处,原始叶型和优化叶型叶片尾缘处的熵分布云图。可以观察到,经过弯掠优化设计的叶型在叶根处的流动损失明显减少,这意味着由于叶型的弯掠作用叶根处的流动分离得到了明显的抑制,因此提升了叶片通道内的流通能力,使流量增加,同时也解释了图14所展现出在叶根处总压比提升效果明显的原因。由图15(b)还可以发现,在叶根处附面层到抑制的同时,由于受到叶片径向力的作用,附面层少量低能流体向其中发生了迁移;而在20%叶高左右的附面层抑制效果不明显,两股低能流体在此处形成堆积,由此产生了一定的流动损失。
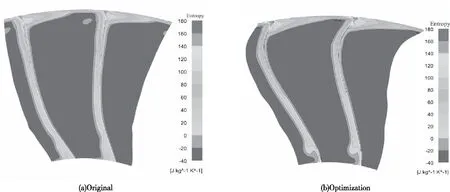
图15 叶片尾缘处熵分布云图
图16给出了设计工况80%叶高处相对马赫数分布云图。可以发现原始叶型通道内为一道斜激波,而弯掠优化叶型的通道内为一道正激波,激波强度有明显增强,因此在图14中所表现出叶尖处总压比有明显提高,而在80%叶高处的绝热效率相比原始叶型却略有降低。

图16 80%叶高相对马赫数分布云图
7 结论
本文建立了一种基于BP神经网络和NSGA-III遗传算法的跨音速转子的优化方法,用该方法对Rotor67转子进行了弯掠组合优化设计,并取得了良好效果。研究得出如下结论:
1) BP神经网络在压气机气动优化设计中能够建立准确的待优化几何参数和CFD计算气动性能参数之间的映射模型。
3)神经网络和遗传算法交替训练的方式对最优解附近的样本进行了加密,使最优解处代理模型精度有了明显提升。
4)在进行两个以上的多目标优化时,NSGA-III所得到的最优解均匀分布在空间的一个连续曲面上;而NSGA-II所得到的最优解集分布较离散,无明显规律。NSGA-III在求解更多目标的优化问题时,具有比NGGA-II更好的效果。这为在多工况多目标优化设计提供了新的技术途径。
5)经过优化的叶型在全工况工作范围内性能均有所提升,不仅提高了其绝热效率,压比,流量,还拓宽了其稳定工作裕度。
