基于Python 的离散随机实验的教学设计

浙江万里学院基础学院综合部 田増锋

本文在Python 的sympy.stats 宏包的基础上设计实现了概率论中离散型随机实验，针对教学中遇到的各种相关问题给出了实验方案，通过概率实验对教与学起到良好的辅助作用。

随着计算技术和算法的发展，尤其是便携式的计算工具(例如各种图形计算器如HP Prime，TI Nspire 等)的普及，原来需要手工计算的一些数学课程引入了数学实验教学方法，即通过各种计算工具或者软件进行数学的探究式学习。

相较于《高等数学》和《线性代数》课程的实验，《概率论和数理统计》课程中的实验基本上是针对数理统计部分的，在概率论部分除了可以使用计算器进行阶乘、排列数、组合数以及积分和导数计算之外，基本上其他的计算仍然是通过手动进行的，在概率论部分缺乏实验环节。

目前在概率论中引入数学实验的主要软件有Mathematica，R，MATLAB，其中R 语言主要功能是统计分析和计算，另外两个商业软件价值不菲，甚至于会掺杂政治因素导致限制其使用。

Python 作为一种开源的，完全面向对象(OOP)的语言，自从出现以来得到了飞速发展，其功能得到快速扩充。在文献[5]中给出了Python 在概率论中的一个初步应用，使用的是逐步计算，没有使用Python 中的随机对象。

在Python 语言的sympy 包中引入了大量的概率论部分的功能，其中包含很多随机对象及其方法，调用这些方法或者函数可以完成基本的概率论实验部分。本文在Python 的sympy.stats 包基础上进行概率论中离散随机变量部分实验教学设计与实现。

1 古典概型实验

在古典概型中运用最多的就是抛硬币和掷骰子实验。这两种随机对象在sympy.stats 中分别定义为Coin 和Die。要进行多次实验则调用sample 函数(要求随机变量取数值结果)即可。

例1：求抛硬币实验的概率分布；进行10 次抛硬币实验。

其中函数density 计算概率分布或者密度，sample 则是进行实验取样，size 是样本大小，S.Half 是sympy 中对1/2 的精确表示。其中的C 和Y 分别表示抛硬币这个随机对象和二项分布随机对象，因为sample 中只实现数值型随机对象的取样，所以这里采用二项分布得到10 次抛硬币的实验结果。

2 离散随机变量

在sympy.stats 中定义了常用的离散型随机变量对象，例如二项分布、超几何分布、泊松分布等，对于一般的有限样本点的离散随机变量也有合适的定义方法。可以对离散随机变量计算其(条件)概率、概率分布、期望、方差、离散变量函数的分布(或期望)等直接计算。

2.1 常见离散分布的概率计算

例2：某公司生产一种产品300 件，根据历史记录次品率为0.01，问现在这300 件产品经检验废品数大于5的概率是多少?

第一种方法，这是300 次独立的Bernoulli 实验，可以进行使用二项分布进行精确计算，其中函数P 用于计算概率。

计算结果: 0.08392，其中最后一句round(5)是进行近似计算的精度设置。

2.2 给出概率分布的一般离散随机变量

例3：已知变量X 取值-1，0，1，2，相应概率依次为1/2c，3/(4c)，5/(8c)，7/(16c)，确定常数c，并计算P(X<1|x ≠0)

实验方案如下，用solve 命令求解方程得到c，然后用FiniteRV 构建离散随机变量，再使用given 函数构造条件概率分布，最后求概率。

这个例子中使用了条件概率及其分布。这里也能直接计算离散随机变量函数的概率分布或者概率。

3 离散随机变量的数字特征

在计算随机变量的数学期望和方差时可以直接调用函数E 和variance 来计算。

例4：已知X 服从二项分布，而且E(X)=3，D(X)=2，求X 的全部可能取值，并计算P(X ≤8)

要计算P(X ≤8)则需要把n 和p 带入，进行9 次Bernoulli 实验需要采用二项分布来计算概率，

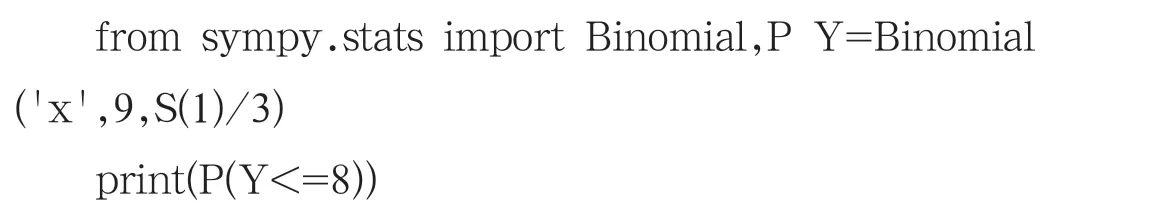
结果:19682/19683，也可以通过。round(10)得到近似值0.9999491947

从这个实验中可以体现sympy.stats 的强大功能在于符号计算，这个功能是Python 中其他的包所不具备的，相当于其他数学实验语言中的符号计算。

例5：设X 服从参数为2 的泊松分布，Y=3X-2，试求E(Y)，D(Y)，cov(X，Y)，以及ρXY。

计算结果:4，18，6，1.在sympy.stats 中没有定义相关系数的函数，这里直接使用定义计算即可。

4 极限定理的验证实验

在概率论和数理统计中中心极限定理有着至关重要的作用。这里分别从直接计算、正态分布近似计算以及蒙特卡洛模拟方法近似验证三种情况进行实验。对于抽象的定理给出一种直观模拟验证。

例6：某公司有200 名员工参加一种资格考试。按照往年经验，该考试通过率为0.8。计算这200 名员工至少有150 人通过考试的概率?

第一种方法，计算精确的概率值作为后续与近似计算比较的依据

from sympy.stats import Binomial, P from sympy import Ge,Symbol

X = Binomial('x',200, 0.8, 1, 0)

P(Ge(X,150))

计算结果:0.965503225134272

结果:0.9616364296，和精确值比较而言用中心极限定理近似计算的精度相当高。

第三种方法，采用Monte-Carlo 方法进行随机模拟实验。

实验结果:0.97,0.945,0.95,0.955,0.975,0.965,0.96,0.965,0.965,0.965....

从结果分析，频率在0.96 附近徘徊，也就是在概率周围浮动，这体现了频率围绕着概率上下波动的统计意义。

5 结语

通过上述离散随机变量的实验可见，Python 的sympy.stats 包中包含绝大多数概率论部分实验中用到的功能，和Mathematica 类似，也是一种面向任务的语言，通过简单的编程即可实现概率论中离散型随机实验。

通过概率论的实验可以将抽象的理论具体化、形象化，可帮助学生理解“学”中的难点，激发学生的学习热情和创新意识，而且应用灵活，可穿插于课堂教学中，亦可设计成独立实验。以计算为模型学习概率论理，让学生在“看得见摸得着”的理论学习中提升自己的专业水平，在深化学生对理论知识理解的同时，提高其运用理论结合工具解决复杂工程问题的能力。

引用

[1] 吴赣昌,主编.概率论与数理统计(第五版)[M].北京:中国人民大学出版社,2017.

[2] 李丽洁,潘伟权,尹誉铭.基于R语言的概率论可视化教学方法[J].中阿科技论坛(中英阿文),2020(7):158-160.

[3] 马永刚,刘俊梅.基于Matlab软件的案例教学在概率论课程中的实践[J].教育现代化,2020(4):150-152.

[4] 解博丽.概率论与数理统计引入MATLAB实验教学手段的必要性[J].教育教学论坛,2020(23):280-282.

[5] 王福顺.Python赋能概率论与数理统计教学与实践[J].中国多媒体与网络教学学报(上旬刊),2021(3):218-220.