旋转悬臂管道流固耦合振动分析
2022-07-19曹建华郭东旭
曹建华,郭东旭,褚 园
(黄山学院 机电工程学院,安徽 黄山 245041)
输流管道在工业中应用广泛,如核工业、化工行业、航空航天等,其流固耦合振动现象吸引了众多学者的注意。在无旋转的输流管道方面,Benjamin[1,2]首先从理论和试验方面较为全面地研究了非旋转的铰接输流刚性管道,Gregory 和Paidoussis[3,4]对非旋转的输流弹性直管进行了研究,并指出了输流管道发生失稳的条件。另一方面,旋转悬臂梁在旋转机械中应用广泛,如机械手臂,直升机旋翼桨叶、风力发电、蜗轮机械等。与非旋转直梁不同的是旋转直梁在动力学模型中多了附加离心刚度项和科氏力项(Houbolt 和Brooks)[5]。基于欧拉-伯努利模型,Du 等人[6]推导了旋转悬臂梁面外振动的自然频率和模态解析解。Yoo 和Shin[7]研究了顶端质量、弹性基础、截面变化、剪切变形等对旋转梁模态特性的影响。另外,Yoo[8]也提出旋转梁的一种建模方法,该方法采用了伸展变形替代传统的3 个笛卡尔变形变量。Cai 等人[9]分别采用了传统零阶近似耦合模型和一阶近似耦合模型研究了旋转梁的动力特性,并进行了振动的主动控制研究。
旋转输流直管结合了输流直管和无流体的旋转直梁的工作特点,而关于旋转悬臂输流直管方面,国内国外的文献相对较少。基于轴线不可伸长假设,Panussises[10]采用牛顿法推导了旋转悬臂输流直管的面内面外两个非线性运动微分方程,应用Galerkin 方法求解了无量纲频率,并没有涉及转速对临界曲线的影响,并将数值结果与前人文献进行对比和验证。BOGDEVIČIUS[11]在忽略转动惯性和剪切变量的假设下,采用了有限元方法离散了旋转输流直管的几何非线性微分方程,求解了非线性微分方程的响应。Yoon[12]基于Lagrange 方程推导了旋转输流直管的运动微分方程,并分析了转速、端部质量和流速对动力特性的影响。
从上可知,旋转输流管道侧重于几何非线性、系统参数等对频率的影响,并未涉及到面内面外振动的对比,也未就旋转悬臂输流管道发生颤振时的临界流速曲线进行分析。本文针对国内外的研究现状,采用Hamilton 方法推导了旋转悬臂输流直管的线性微分方程,采用小波有限元方法离散微分方程,构建了小波有限元单元矩阵,求解了面内面外的临界流速曲线,分析了转速对临界流速曲线的影响,以及面内和面外振动的区别。
1 旋转输流直管的微分方程推导
基于轴线不可伸长的假设,水平放置的旋转输流直管几何和坐标如图1 所示,管道长为L,不可压缩活塞流体的流速为U,正交坐标系(x,y,z),输流管道绕着y 轴转动,角速度为Ω,(u,υ,w)分别为3 个方向上的位移。
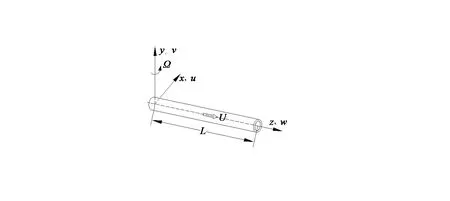
图1 旋转输流直管的几何和坐标


2 微分方程的小波有限元解法

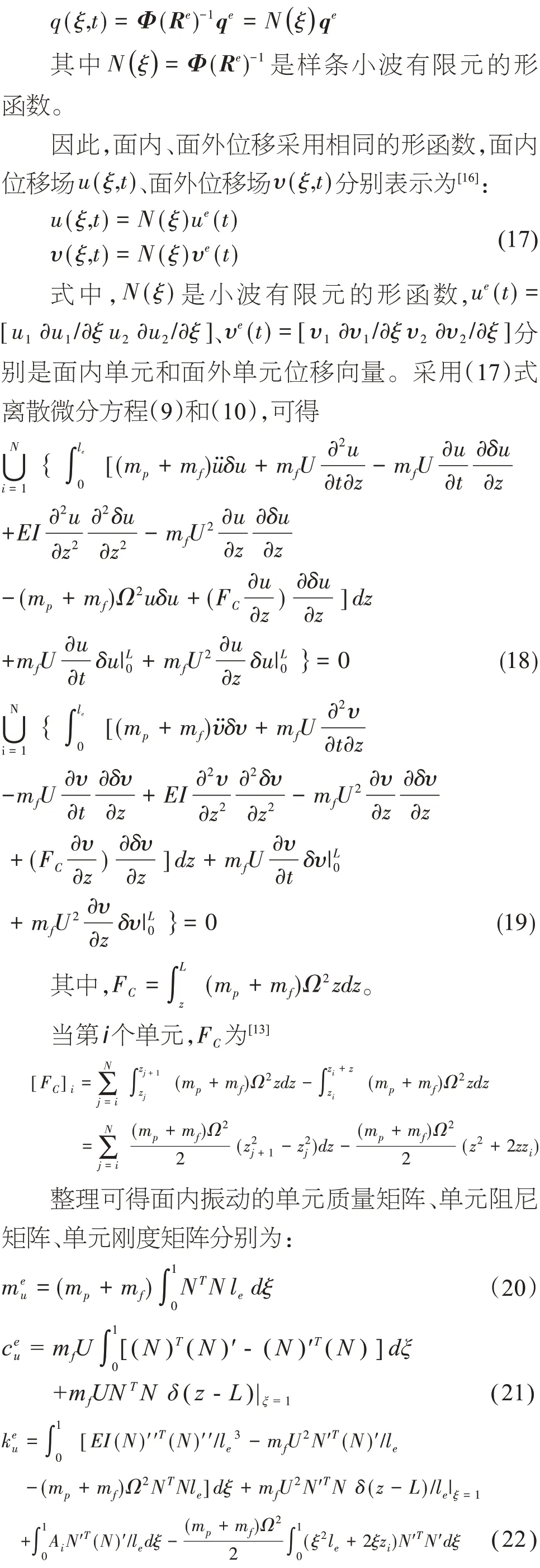
面外振动的单元质量矩阵、单元阻尼矩阵、单元刚度矩阵分别为:
其中()·和()′分别表示∂()/∂t和∂()/∂ξ。
采用经典有限元单元组装方法,可以得到系统质量矩阵,系统阻尼矩阵,系统刚度矩阵和系统位移向量。

3 数值算例

根据Paidoussis 所述方法[15]:在计算中,固定流速U,设定β 从0 开始,按步长增加,αr开始小于0。当质量比β 增加到某一数值时,所得特征值中最大的αr接近0 或大于0,悬臂输流管道发生颤振失稳,此时流速,即为此质量比对应的临界流速Ucf。
本节首先在流体流速U=0 和不同旋转转速情况下,采用2个小波单元计算了面内频率,并与前人文献相对比,如表1所示。从表中可以看出,在相同的质量比情况下,随着转速增大,频率也随之增大;在相同的转速下,随着质量比增大,频率也增大。在与文献[10]比较可以发现,两者结果相差不大,频率最大误差不超过1.9%。分别采用6 阶伽辽金法和4个小波单元,求解旋转悬臂输流直管的临界流速曲线,如图2所示,在质量比小于0.9时,两种方法所得的临界流速曲线转折点基本保持一致,数值结果相差不大;质量比大于0.9 时,两种方法的数值结果开始出现差异,质量比越接近1 时差异越大。综上所述,在质量比不在1附近时,本文方法所得数值结果可靠和准确。
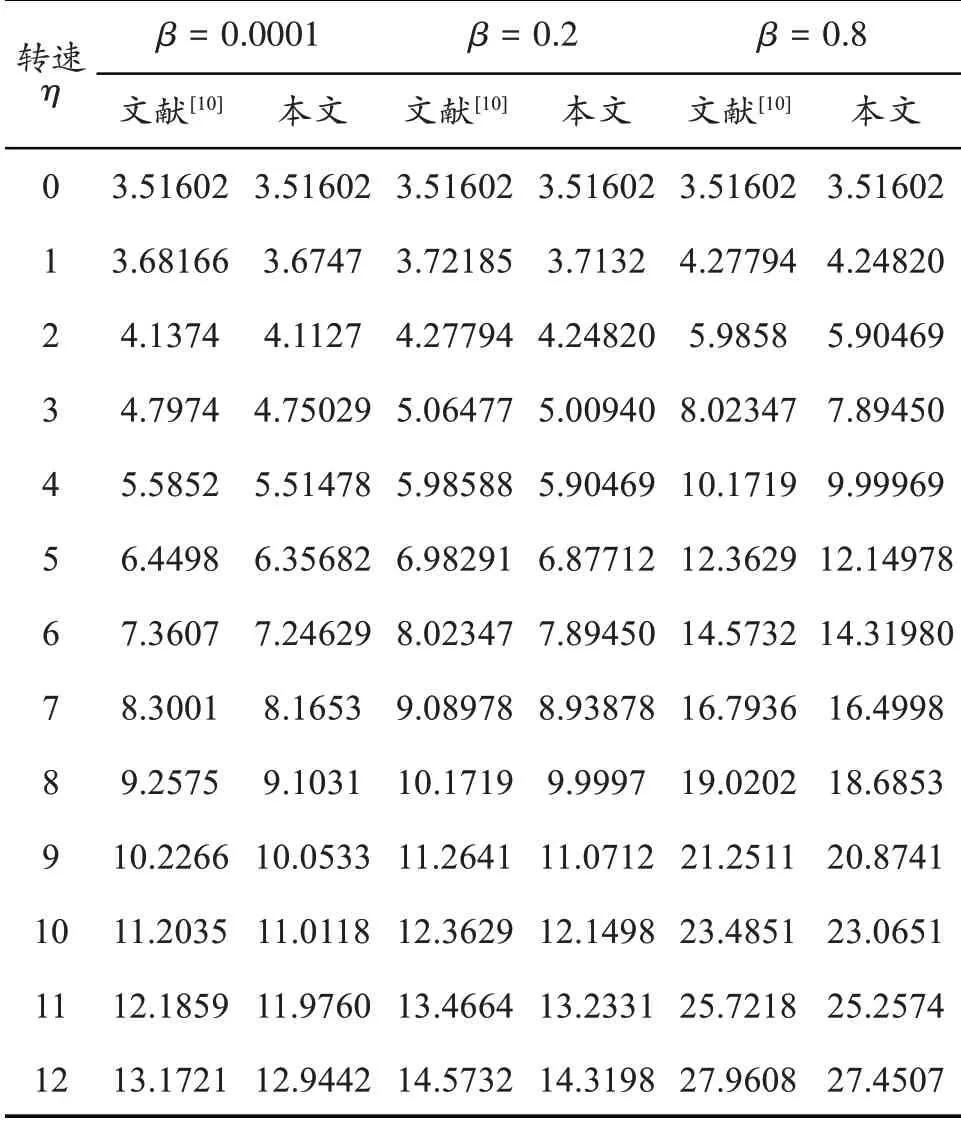
表1 不同转速下旋转输流管道面内无量纲频率对比结果

图2 临界流速的伽辽金法和有限元法数值结果比较
计算在不同转速下旋转悬臂输流直管的临界流速曲线如图3 所示,S 形状区域表示模态的改变,管道发生颤振。不同旋转转速下面内和面外振动的临界流速曲线随质量比的变化趋势是相同的,随着转速的增大,临界流速越大,临界流速曲线的稳定区也随之增大。比较在同一旋转转速下面内和面外振动的临界流速曲线,如图4所示,在转速较小时,面内和面外振动的临界流速曲线相差不大,在η=0时是重合,在η = 2时是几乎重合,之后随着转速的增大,面内面外的临界流速曲线相差变大,面外的临界流速大于面内临界流速。这说明面内比面外先发生失稳,主要因为面内比面外的微分方程多了一项由于旋转转速产生的离心力项-(mp+
mf)Ω2u。
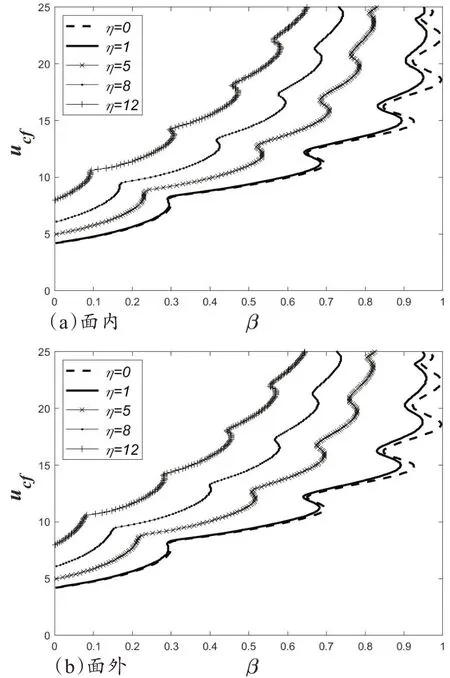
图3 不同转速下面内和面外振动的临界流速曲线比较
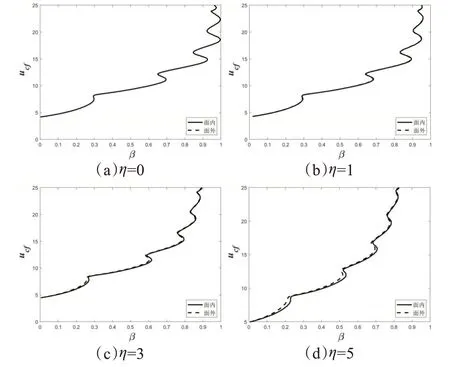
图4 不同流速下面内和面外振动的临界流速曲线比较
4 总 结
本文基于哈密顿方法推导了旋转悬臂输流直管的线性振动微分方程,利用小波有限单元法离散了微分方程,求解频率和临界流速曲线,并与前人文献对比,证实了数值结果的可靠性和准确性。通过比较面内和面外振动的临界流速曲线可得,随着转速的增大,临界流速越大,临界流速曲线的稳定区也随之增大,且面外的临界流速大于面内临界流速,面内面外的临界流速曲线差值增大。因此,对于旋转悬臂输流管道,面内振动比面外先发生失稳,在旋转机械设计中应着重注意。
