一种新的可计算可压缩流动的预处理方法*
2022-07-19刘博邢朴丁松谢明军冯林时晓天
刘博 邢朴 丁松 谢明军 冯林 时晓天†
1) (中国航天空气动力技术研究院,北京 100074)
2) (北京航空航天大学航空科学与工程学院,北京 100083)
3) (北京航空航天大学大型飞机高级人才培训班,北京 100083)
4) (南开大学数学科学学院,天津 300071)
针对使用可压缩流动数值方法求解不可压缩流动存在的刚性问题,基于虚拟压缩法思想,构造了一种以Mach 数、速度、密度、温度等变量为元素的预处理矩阵,改变了控制方程组的特征根并使其量级更接近.通过理论推导与分析,证明新方法相比Weiss,Pletcher,Dailey 和Choi 的方法而言,不仅能降低方程组的刚性,提高了数值求解效率,而且拥有更好的稳定性,此外还能实现低速流动和高速流动之间的光滑过渡.采用有限差分格式进行离散,对流项的Roe 格式作为基本加权无振荡(WENO)格式的求解器,黏性项则使用中心型紧致差分格式来计算,与预处理矩阵相结合展开数值实验,结果表明新预处理方法可以实现对无黏和有黏不可压缩流动问题的高精度模拟,且拥有比Weiss 和Pletcher 等提出的方法更好的收敛性和稳定性.
1 引言
计算流体力学(computational fluid dynamics,CFD)是流体力学、计算数学与计算机技术相结合而发展起来的新兴学科,它通过数值仿真和可视化处理,对流体流动和热传导等物理现象进行计算机数值分析和研究.其中有限差分法[1−3]是应用最广泛、最成的方法之一.
随着CFD 的不断发展,人们所求解的问题也日益复杂化,这些问题通常归结为高速和低速流动问题,高速流动需采用可压缩流动计算方法[4,5],而低速流动采用不可压缩流动计算方法[6−8].然而,这两种方法的特性存在很大差别,例如,高超声速往往伴随着如激波一类的强间断存在[9],亚声速流动的流场中任何微小的扰动都将影响整个流场[10],因此具体数值方法要在特定环境下使用.针对高速的可压缩流动数值求解问题,学者们已研究出较成熟的理论,而面对低速流动时,无论采取显格式还是隐格式计算,速度越小对计算误差和收敛速度影响越大,这也被称为刚性问题[11,12],这种刚性给数值方法带来了很大的困难.
同时,不可压缩流动数值方法在实际工程应用又有很大的需求,如翼型绕流,边界层内流动[13−15].在某些问题中,还会出现高低速流动并存的现象[16−18].为了求解此类问题,需要发展能够有效求解低速流动的数值方法.为了求解有很强不可压缩性的低速流动问题,Fasel[19]提出涡函数-流函数法,Aziz[20]提出势函数-流函数法,其本质是引入流函数和涡函数并对控制方程进行变换,但是壁面处涡量难以处理,而且推广到三维问题后过于复杂.Halrow 和Wetch[21]提出格子中标记点算法(marker in cell,MAC),Hirt 等[22]则在MAC 算法上加以改进提出SOLA 算法,此类方法可以有效地处理含有复杂的自由面或界面的流动,但是对时间步限制非常严格,所以求解效率较低.Spalding 和Patankar[23]提出压力联系方程的半隐式法(semi implicit method for pressure linked equations,SIMPLE),该方法核心在于不断修正压力项,通过修正后的压力求解速度并满足连续方程,直到收敛.为了提高收敛速度,Patankar[24]又提出SIMPLER (SIMPLE revised)算法,van Doormaal 和Raithby[25]提出SIM PLEC (SIMPLE consistent)算法,Minkowycz 等[26]提出SIMPLEX (SIMPLE extraplation)算法,Issa等[27]提出PISO (pressure implicit with splitting of operators)算法,他们都通过加强速度与压力的耦合来达到加速收敛.但是这类方法占用内存很大,插值过程繁琐,大量时间都消耗在修正压力项上,且编程复杂.
实际上,不可压缩流体是为了简化某些问题提出的理想模型,任何流体都是可压缩的.而且很多时候热量的影响是不可忽略的[28],质量、动量和能量方程需要耦合在一起求解.鉴于可压缩流动的数值方法相对成熟,因此有研究者提出使用计算可压缩流动的数值方法来计算不可压缩流动问题.Chorin[29]于1967 年提出虚拟压缩法就是基于这种思想,这也成为了预处理方法的雏形,该方法另一优势是可将高速与低速流动统一在同一算法框架下求解,避免了切换数值方法的繁琐和交换信息而产生的精度损失.最早的预处理矩阵由Turkle[30]于1986 年提出,其核心作用在于改变时间导数项,减小方程组特征速度的量级差异,1993 年Choi 和Merkle[31]提出与Chorin-Turkel 矩阵相似的适用于Euler 方程的预处理矩阵.最早适用于全速域的预处理矩阵是由Viviand[32]设计的四参数矩阵,但在驻点附近刚性依然很强.针对Navier-Stokes 方程,Choi 与Merkle[33]以及Buelow 等[34]提出了考虑Reynolds 数的影响的预处理矩阵,Godfrey 等[35]提出的矩阵将Euler 处理矩阵结合了离散方程的黏性/无黏性的块Jacobi 矩阵,但仍然难以降低驻点附近的刚性.Weiss 等[36],Pletcher 和Chen[37]提出的矩阵形式简单,且降低了驻点附近刚性,被广泛的应用于FLUENT,OVERFLOW 等商业软件.Dailey 和Pletcher[38]提另一种矩阵并将其与多重网格法结合.且预处理方法不仅可以与有限差分法搭配,也可以与有限体积法[39]、间断有限元法[40]搭配,此外也可以与双时间步技术结合用于计算非定常问题[41].
本文提出一种新的预处理矩阵,该矩阵引入了两个关于Mach 数的函数b和ML,使得方程组的刚性进一步降低,在确保(甚至能提高)精度和稳定性前提下加速了收敛速度,并且在高速与低速流动之间过渡更加光滑(其中ML在有黏和无黏情况下拥有不同的形式).通过数值实验,初步证明了本文方法的可靠性,并与其他方法相对比,体现本文方法的优势.
2 基本概念
2.1 物理量的无量纲化
为了方便实现数值实验的相似模拟,本文对变量采取了如下无量纲化处理:

其中,x,y,z代表空间直角坐标系的三个坐标分量;L代表参考长度;t代表时间;u,v,w分别代表三个坐标轴方向上的速度;g代表重力加速度;ρ代表密度;E为单位体积流体的总能量;c代表声速;T代表温度;µ为黏性系数;上标“ * ”代表有量纲量,下标“ ∞ ”代表参考值;下文2.2 节中的Re为来流Reynolds 数,Reρ∞c∞L/µ∞.
2.2 流体力学控制方程组
Navier-Stokes 方程组是流体动力学中最重要的基本方程,它是黏性流体微团应用牛顿第二定律得到的运动微分方程.以三维可压缩流动的情形为例,忽略外加热源和彻体力的无量纲化方程:
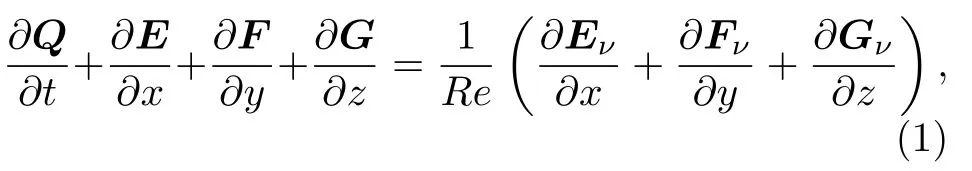
其中
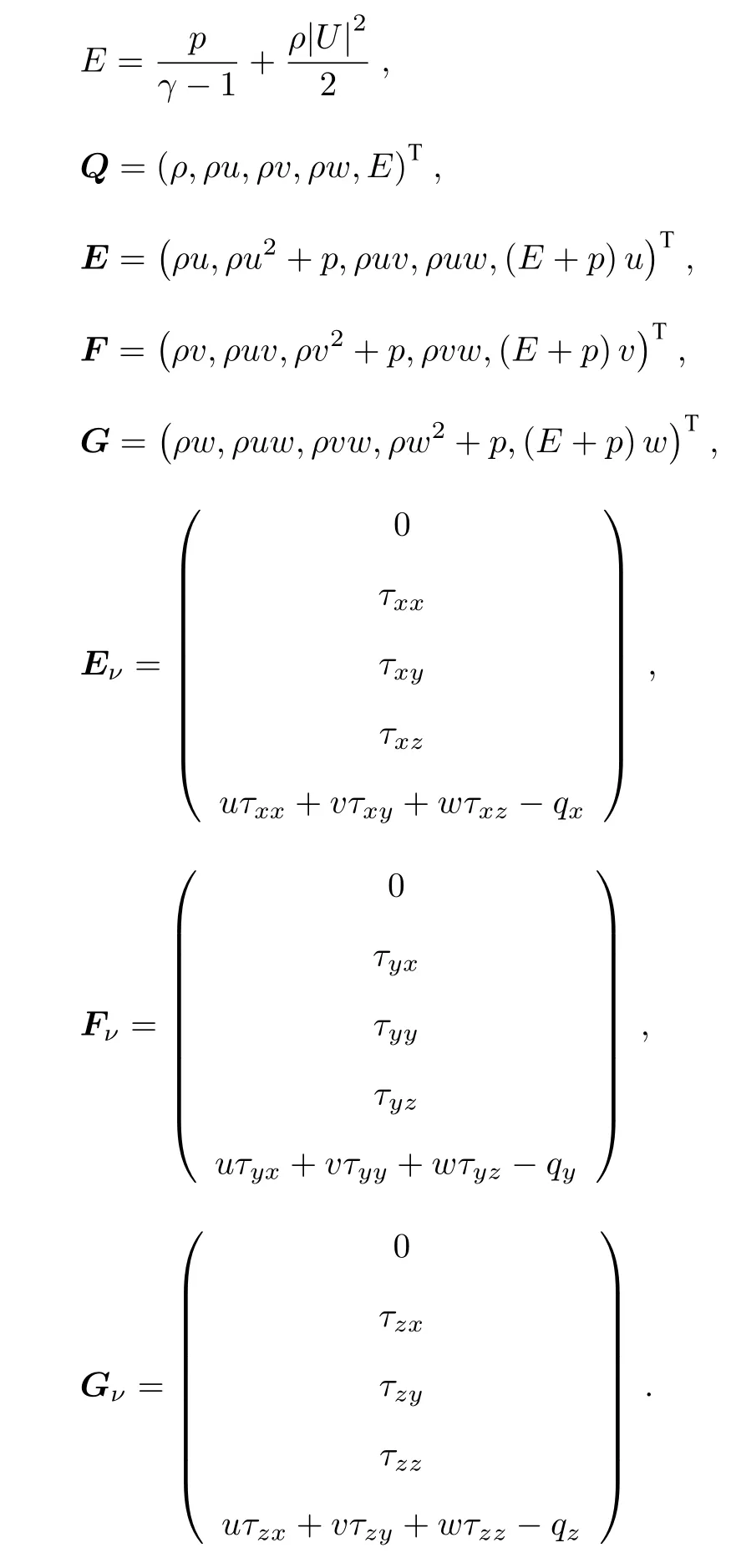
黏性应力项与热传导流通量分别为
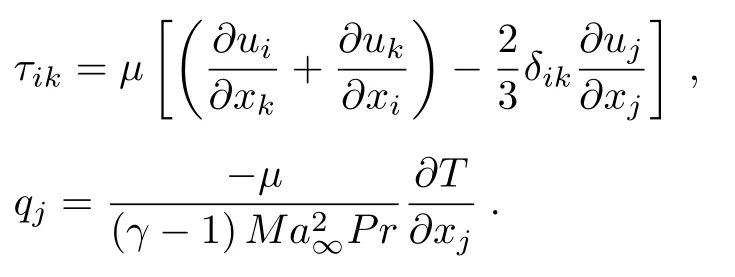
其中当i=j时,δij=1,如果i≠j,δij=0;Pr是Prandtl 数;U代表速度矢量,对于无黏流动,(1)式的右端为零.在实际的应用中,经常会用到曲线坐标系形式的方程组,具体如下:
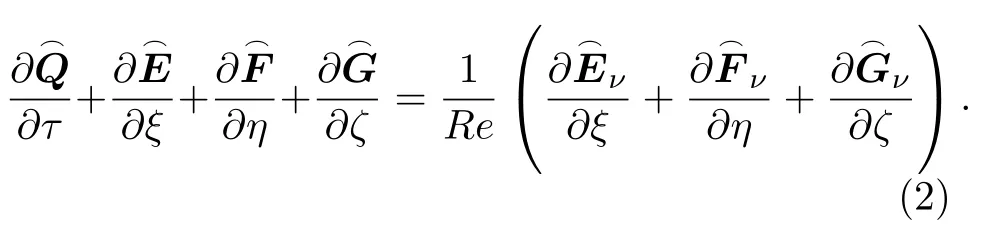
这里 (ξ,η,ζ) 为曲线坐标系.

本文采用的是方程组(2),并取τ=t,后文将省略该方程组中变量的上标“⁀”.
3 方程组的刚性问题
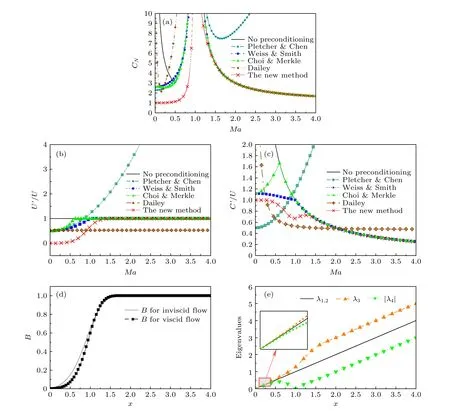
3.1 预处理方法
使用与时间相关的可压缩流动数值方法来求解不可压缩流动时,方程组的特征根量级差异过大(也称刚性过大),这会严重影响计算的收敛性.基于虚拟压缩法原理的预处理法可以有效地解决这一问题,即在时间导数项前乘上个预处理矩阵,改变方程组的特征系统.虽然改变了方程组形式,但对于定常问题而言,经过足够长的时间后取得的收敛解不会受此影响.为了更好地计算黏性问题,通常在带预处理矩阵的控制方程中使用原始变量QT(p,u,v,T)T,下面以二维带预处理矩阵的有黏性控制方程为例:
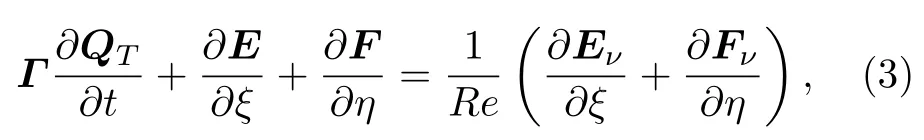
其中各变量与通量意义同前文所述.Γ是预处理矩阵,其形式有多种,常见的形式有Weiss-Smith 矩阵[36]:
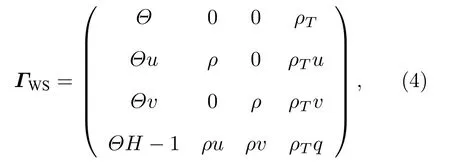
其中

k0通常取1,如果是有黏方程,还要限制:
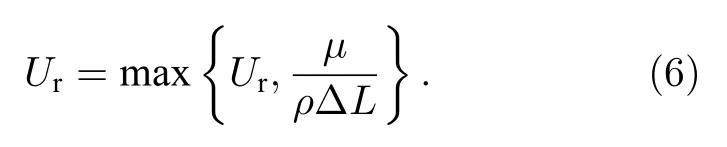
Weiss 与Smith[36]构造参考速度Ur,是为了既能在Ma较大时,让预处理矩阵还原成非预处理状态,又能Ma较小时,减小方程组刚性.此外,对于黏性流动而言,还需要限制Ur不小于局部扩散速度µ/(ρΔL),这种限制在扩散作用为主导且网格间距较小的情况下是有必要的.对预处理后的特征根的讨论详见3.2 节.
Pletcher-Chen 矩阵[37]:

其中
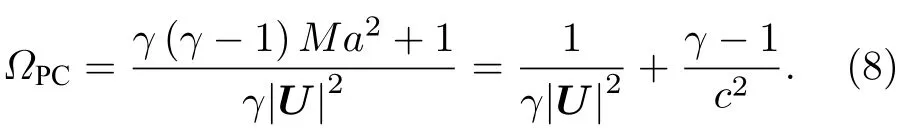
Choi-Merkle 矩阵[33]:
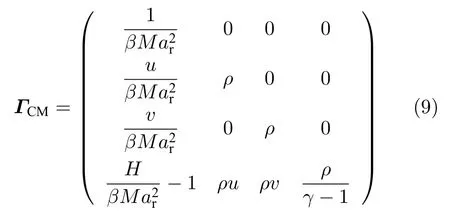
其中
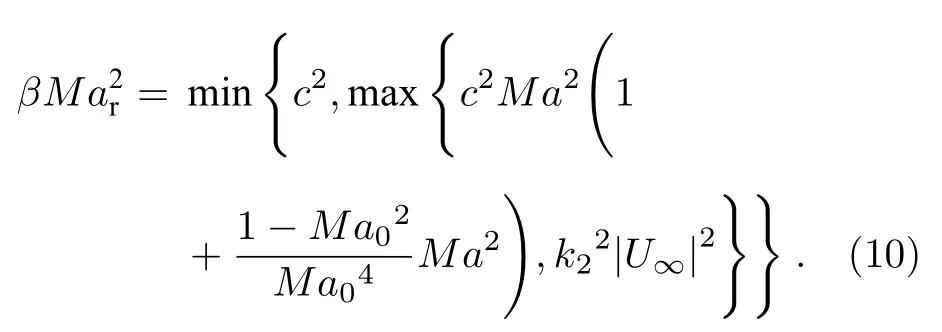
Ma0是参考Mach 数,k2是常数,通过大量实验发现,Ma0取0.5,k2在Euler 方程时取0.5,在NS 方程时取1,这样有利于长时间运算的稳定性.该方案是Choi 与Turkle[31]提出的,其作用是为避免驻点附近预处理矩阵的奇异性,对βMar2实施一定的人为控制.
3.2 特征系统分析
如果不预处理,则方程(3)应该为
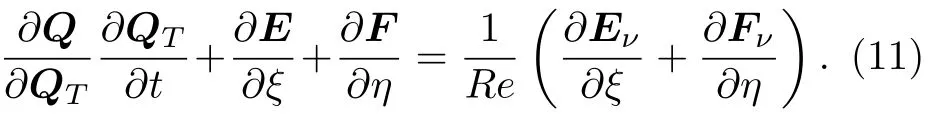
将(11)式等号左端全部替换成以QT为变量的形式:
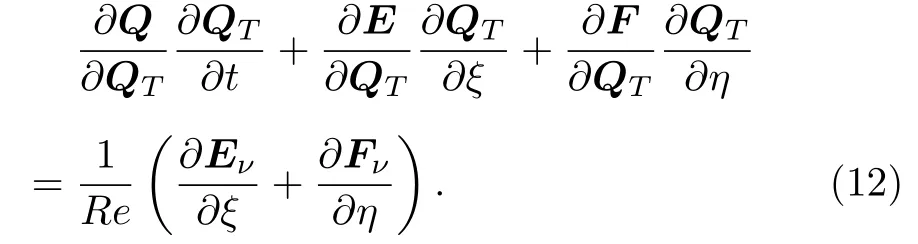
即
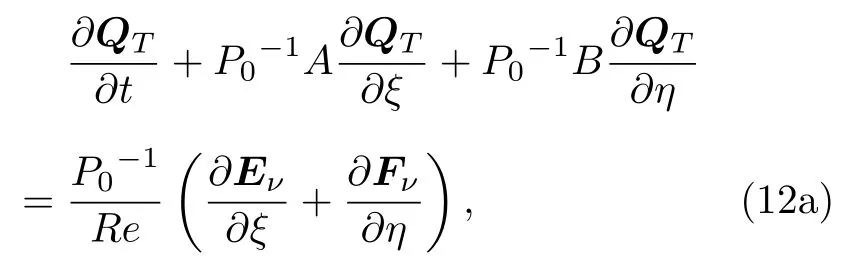
其中守恒变量Q到原始变量QT的Jacobi 变换矩阵为
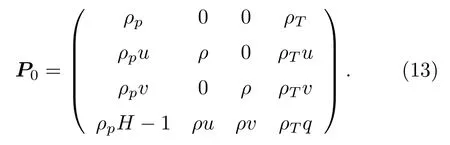
下面以直角坐标系的ξ方向为例分析预处理前后方程组的特征系统:
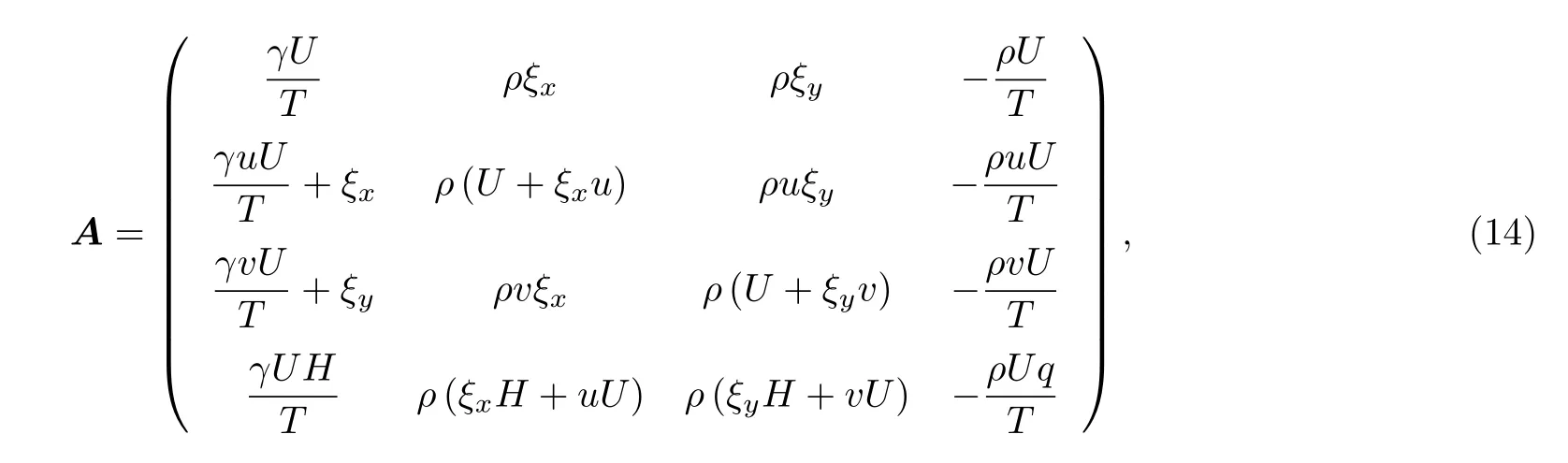
其中
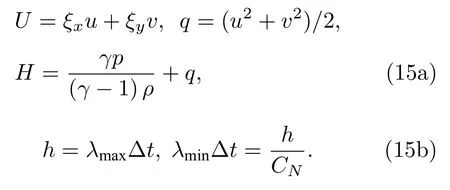
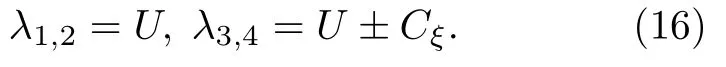
特别地,当ξx,ηy时有
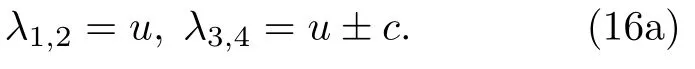
条件数通常用来衡量方程组的刚性大小,当u→ 0 时:
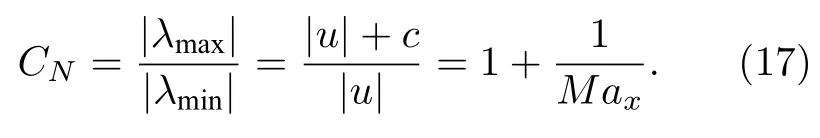
假如快波传输了1 个网格的长度,则有
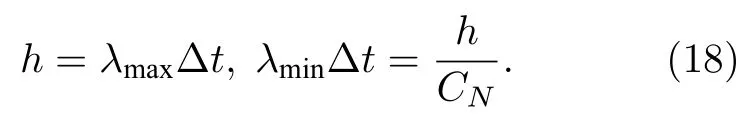
可见,当条件数非常大时,相同时间内快慢波传播的距离会相差很多数量级,这给方程的求解造成很大困难.若使用预处理矩阵替换P0,则由Choi[31],Pletcher[37]和Weiss[36]等提出的预处理法得到的特征根都有相同的形式:
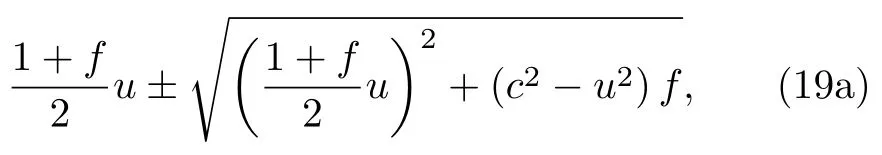
其中f是关于Ma的函数,虽然每种预处理法都不一样,但该函数都是改变特征根的关键所在.以Weiss-Smith 形式为例:
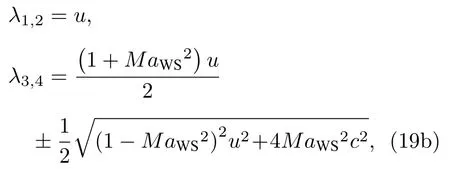
其中Ur同(5)式:

当Mach 数很小时,特征根依然能保持在相近的量级范围内,刚性得到降低,条件数的取值范围被限制在1 对此,本文设计了一种新的预处理矩阵,使得方程组在预处理与非预处理之间的过度更加光滑,并进一步降低了特征系统的条件数,从而增加收敛效率,并且拥有良好的精度和稳定性. Turkle[30]曾在Wiess-Smith 矩阵[36]基础上加以改进,增加一个参数从而提高预处理矩阵的灵活性,其矩阵具体如下: 式中 其中δ为根据求解需要选定的0—1 之间的常数,βMar2同(10)式.本文受Turkel 引入调节参数δ的启发,引入调节函数b1,b2和ΩL,这些函数会随着流场中某些物理量的变化而变化,从而可实现对预处理矩阵动态调控,具体形式如下: 其中 εm是防止ML=0 的一个小量,本文取εm=10–6.若Reynolds 数较小,则需限制其不小于局部扩散速度,同时既要避免驻点附近的奇异性,又要保证ML函数的光滑性,还要保证后文中伪声速的光滑性,转化为数学分析语言: 1)ML函数在(0,1)上为单调递增的至少C1连续函数,且(1)=0. 2) 当x→ 0 时,ML(x) → 0;ML(1)=1. 3) 若ML≤µ/(ρc△L),则ML=µ/(ρc△L);若ML≥ 1 时,则ML=1. 根据以上原则构造出如(24c)式的ML函数,其中εm同(24b)式: b1,b2是与Ma相关的函数,可以相等也可以不相等,在本文中取b1=b2=b,具体的有 为了在低速时进一步降低方程组刚性,在高速时还原成原方程,需使得 1) 当Ma=0 时,B=0;当Ma≥ma0时,B=1. 2) 当0 3)B'(0)=B''(0)=B'(ma0)=B''(ma0)=0. 4) 在全Mach 数范围内,需要满足λ3>λ1,2>|λ4|. 5) 在Ma 6) 在Ma >ma0时,要求λ3/λ1,2,|λ4|/λ1,2分别逼近未经预处理时的λ3/λ1,2,|λ4|/λ1,2. 7) 使B函数在左右端点Ma=0 和Ma=ma0附近应保持变化缓慢,从而抑制速度u在低Mach数和临界点处由于预处理作用而出现的剧变. 8) 与(24c)式的ML匹配,使得后文中伪声速具备良好的光滑性. 按照以上8 条要求,本文构造了如(25b)式的B函数: 其中ma0是事先给定的常数;n1,n2是正整数;CL是常数.为了使B满足上述5)—7)性质,且尽可能使特征根差异最小,并使经与处理后的特征根满足λ3>λ1,2>|λ4|,计算无黏和黏性很小的流动时,选择: 如果黏性不可忽略,可以令 函数B的图像可见图1(d).通过简单运算可知该矩阵的行列式为 图1 经不同预处理方法后的特征系统(对于每种预处理后的速度有,U'=(λ3+λ4)/2,C'=|λ3–λ4|/2,均为无量纲化速) (a) 条件数CN;(b) 伪速度U';(c) 伪声速C';(d) B 函数;(e) 本文预处理法得到的特征根Fig.1.Characteristic system of the governing equations obtained after different preconditioning:(a) Condition number;(b) pseudospeed;(c) pseudo-sound speed;(d) function B;(e) the eigenvalues obtained after preconditioning in this paper. 可见,该矩阵恒为可逆矩阵.此时的预处理矩阵在计算低速问题时效果较好,如果用于跨声速和全速域问题的计算,可以选取ma0=Mamax(此最大Mach 数是实验前的估计值). 3.4.1 特征值和方程组刚性 下面来定量分析该处理法得到的特征系统.在二维曲线坐标系 (ξ,η)中,以ξ方向为例,求出经ΓLiu预处理后Euler 方程的特征根: 其中伪速度和伪声速分别为 U,Cξ意义同(16) 式,预处理参数选用(26a) 式,且U在(0,ma0U)上时,λ3为关于Ma的单调递增函数,与未经预处理时特征根随速度U增加而变化的趋势一致.经过ΓLiu预处理后的特征根受两个函数B和ML调控,形式上比Weiss,Pletcher和Choi 等得到的特征根(19a)式拥有更多自由度.当Ma→ 0 时有 此时所有特征根在不考虑正负号的情况下为等价无穷小,即在Ma很小的时候,条件数趋于1.先证明对于任意Ma >εm,有λ3>λ1,2>|λ4|. 当Ma≤1 时: 当1 当Ma>ma0时: 由此可知对于任意Ma >εm有λ3>λ1,2,同理可证λ1,2>|λ4|,这也与未经预处理的特征根的大小关系一致,图1(e)更直观地展示了预处理后的特征根大小关系.如果ma0>则会出现Ma0>εm,使得λ3<λ1,2,因此需要限制ma0≤,故上文选取ma0=1.73.λ3,λ1,2恒为正值.当Ma<1时,λ4<0;当Ma>1 时,λ4>0,与未经预处理时特征根的符号相同.特殊地,选取直角坐标系,可以求出其特征系统的条件数满足: 当Ma >ma0时,预处理矩阵退化成P0,方程恢复成原控制方程.图1 为控制方程经ΓWS,ΓPC,ΓCM,ΓD以及ΓLiu预处理后系统的条件数随Ma的发展趋势.从图1 可见,ΓD在Ma∞附近效果良好,在驻点处刚性很大,经ΓLiu处理后的系统刚性小于其他方法,且特征根随着Mach 数从附近增大到Ma>ma0时的变化过程是光滑的,当Ma超过ma0后,伪速度和伪声速都还原成真实速度和声速.由于 其中CFL 数是差分法中判断收敛的条件数,当CFL 数固定时,|λmax|减小可以增大时间步长,从而达到加速效果. 3.4.2 特征根的连续性 下面证明特征根λi关于 (ξ,η) 的连续性,以直角坐标系的x方向为例,注意到(28)式中U′,是关于Ma以1 和ma0为分界点的分段函数,只需要证明分界点处连续性.经无量纲化后,不考虑y方向的速度影响,则有Ma=U=u,从而U′,均可视为Ma(或u)的函数,那么有 当u存在关于x的二阶连续偏导数时,只需验证U′关于u的可导性.对(29a)式和(29b)式分别在(0,1),(1,ma0),(ma0,+∞)上关于u求导,可得 而B在(0,+∞)上存在关于u的二阶连续导函数,那么易证: 即U′存在关于x的二阶连续偏导数,同理可证也存在关于x的二阶连续偏导数.即经ΓLiu预处理后得到的,只要u存在关于x的二阶连续导数,λi亦存在关于x的二阶连续导数.从而克服了ΓWS,ΓPC和ΓCM预处理后的特征根,在预处理和非预处理间过渡不够光滑的缺陷,图1(a)—(c)也可反映出这点. 采用Roe 的通量差分格式作为Riemann 求解器[42],下面以ξ方向介绍该方法,其他方向与之同理.带预处理的Roe 格式可以表示为 其中 ΛΓ是ΓLiuA的特征根,即(28)式组成的对角矩阵,A的意义同(14)式,MΓ是将其化为对角矩阵的变换矩阵,即 此处|ΛΓ|表示将该矩阵所有元素取绝对值后组成的矩阵.高精度的通量E(Q)L和E(Q)R采用5 阶WENO-JS 格式来求得,此过程可详见文献[43].对于黏性项的离散,本文采取一种4 阶紧致的中心差分格式,具体可见文献[44]. 为了与空间离散的精度相匹配,采取三阶显式Runge-Kutta 法做时间推进[45]: 本文仅是对新预处理法的合理性和可靠性进行检验,故选取较为简单的定常流动来验证.如用于非定常流动计算,预处理会破坏时间精度,因此需要做特殊处理.这里介绍一种应用较广泛的双时间步法,其本质是在控制方程中填入一项关于伪时间τ的导数项,并对其做预处理,即 其中τ和t分别是伪时间和真实物理时间,其余物理量同(3)式所述.当τ→ ∞时,上式因左边的第一项消失而复原为方程.分别对τ和t离散,该方法包含两个循环,即伪时间τ的内循环和物理时间t的外循环,在每个物理时间步当作定常问题用伪时间推进求解,无需时间精确的伪时间内迭代可以采用预处理加速收敛.当解的残差变化稳定后,即达到当前物理时间步的真实解,随即物理时间t外循环推进至下一步,然后进行伪时间的内迭代并重复上述步骤,最终得到欲求时刻的非定常解. 下面选取一维有精确解的方程组,平板层流边界层,方腔顶盖驱动,凸鼓包管道流动等定常问题来验证本文方法的可靠性、收敛性和稳定性.由于ΓD在远离Ma∞的效果不如其他方法,文献[46]的实验说明了使用Weiss &Smith 和Choi &Merkle矩阵的效果接近,故本文选取Weiss &Smith,Pletcher &Chen 和本文提出的预处理矩阵进行实验,并对比得到的结果.算例5.1 采用matlab2019 编程,算例5.2—5.4 采用fortran90 编程. 选取有定常精确解的一维Euler 方程组,以QT(p,u,T)T为变量: 其计算域为0 由表1 可见,当k=0.5 时,速度u会经历从小于1 (无量纲化)到大于ma0的跨越,使用本文的预处理法可以在保证精度的同时实现从预处理还原到不处理的连续过渡;在相同的计算时间t=100 下,使用预处理方法比未处理得到的数值解精度高出约1—2 个量级.增加一倍的计算时间,到t=200 时刻未用预处理的解的精度才勉强达到t=100 时刻使用预处理的精度.当k进一步减小时,预处理的效果更加明显,从图2(c)—(f)可以清晰地看出,预处理比不处理收敛速度更快.这表明本文的预处理方法能够在保证精度的同时,提高计算的效率. 图2 数值方法得到的解曲线与精确解曲线 (a) k=0.5;(b) k=0.04;(c) k=0.01;(d) k=5×10–3;(e) k=1×10–3;(f) k=2×10–4Fig.2.Solution curves obtained by numerical solution and exact solution curves:(a) k=0.5;(b) k=0.04;(c) k=0.01;(d) k=5×10–3;(e) k=1×10–3;(f) k=2×10–4. 表1 数值解与精确解之间的误差Table 1. Errors between numerical solutions and exact solutions. 一长为L的平板静置在水平面上,从左侧的与平板平行的均匀来流通过其上表面,以板长为参考长度,以来流处的声速为参考速度进行无量纲化,给定来流速度u∞=0.1,基于板长的Reynolds数Re∞=106,设定来流处压强和温度以及出口的压强,计算网格为180×50,其中x方向为均匀网格,y方向随着y减小而加密,贴近平板上表面的第1 层网格厚度为0.002,CFL=5.计算到收敛后,选取x=0.8 处的速度u随y的分布,并与Bulsius 准解析解对比,对比结果如图3 所示,其中 图3 Ma=0.1 时边界层流动的速度剖面Fig.3.Velocity profile of the boundary layer flow when Ma=0.1. 本文预处理法的收敛速度同Weiss &Smith和Pletcher &Chen 方法的对比如图4 所示.可见,本文的预处理方法得到的数值解与Blasius 解基本一致.由图4 可见,本文方法的收敛效率略好于Weiss &Smith 和Pletcher &Chen 方法. 图4 边界层流动的收敛历程Fig.4.Convergence histories of the boundary layer flow when Ma=0.1. 此算例描述的是一边长为1 (此算例中变量均无量纲化)的正方形空腔,初始Mach 数Ma0=1,顶盖以u0=1 速度向右运动,Reynolds 数分别为100,1000,10000.计算网格为60×60 成中心对称的非均匀网格,并在壁面附近加密,CFL=100,分别使用本文预处理法和Weiss &Smith 和Pletcher &Chen 方法计算此问题.图5—图7 是计算到收敛后得到的空腔内部流场线图,可以观察到,在空腔的几何中心附近产生一个大涡,在底部两角附近产生两个较小的涡结构.随着Reynolds 数的增大,大涡中心逐渐向空腔几何中心移动,底部小涡逐渐增大,当Reynolds 数为10000 时,左上角附近也产生一个涡结构.图8 是本文水平与垂直中心线上速度与使用多重网格法的计算结果[47]的对比,图9 是三种预处理法的收敛速度对比. 图5 Re=100 时的空腔流线图 (a) 本文方法;(b) Weiss &Smith 方法;(c) Pletcher &Chen 方法Fig.5.Velocity streamline diagram of cavity,Re=100:(a) The new method;(b) method of Weiss &Smith;(c) method of Pletcher &Chen. 图6 Re=1000 时的空腔流线图 (a) 本文方法;(b) Weiss &Smith 方法;(c) Pletcher &Chen 方法Fig.6.Velocity streamline diagram of cavity,Re=1000:(a) The new method;(b) method of Weiss &Smith;(c) method of Pletcher &Chen. 图7 Re=10000 时的空腔流线图 (a) 本文方法;(b) Weiss &Smith 方法;(c) Pletcher &Chen 方法Fig.7.Velocity streamline diagram of cavity,Re=10000:(a) The new method;(b) method of Weiss &Smith;(c) method of Pletcher &Chen. 通过图8 和图9 可知,本文提出的方法精确度略高于Weiss &Smith 和Pletcher &Chen 方法(这两种方法的精度对比可参考文献[46]).本文方法的收敛速度也更快一些,且随着黏性效应增加(Reynolds 数减小)效果越明显,这表明本文格式可以实现对低速有黏问题的高精度高效率的模拟. 图8 本文预处理后的中心线速度分布 (a)水平中心线上的速度v;(b)垂直中心线上的速度uFig.8.Velocity along lines through geometric center caculated by the new method:(a) v-velocity along horizontal center line;(b) vvelocity along horizontal center line. 图9 方腔流动的收敛历程对比 (a) Re=100;(b) Re=1000;(c) Re=10000Fig.9.Convergence histories of the the laminar flow in a square cavity:(a) Re=100;(b) Re=1000;(c) Re=10000. 此算例[48]目的在于验证本文提出的预处理方法在曲线坐标系下的计算性能,故选择下表面带鼓包的二维管道流动问题,该算例模型和流场相对简单,便于对结果进行分析.具体模型如下:管道的长度为3 (单位均无量纲化),高度为1,凸鼓包位于下表面的中心位置,长度为1,其尺寸为y=0.1sin2πx(1 图11 为三种方法的残差收敛曲线对比.Ma0=0.05 时三种方法得到的流场Mach 数等值线分布见图12(a)—(c).图12(d)为在加密网格(600×200)下使用Weiss &Smith 法计算得到的流场,并将其作为准精确解.在低速流动下,该流场的Mach 等值线接近轴对称.可见本文方法的计算结果与准精确解基本一致,相比另外两种方法精度更高,尤其第3—5 条等值线的位置.另外本文方法的收敛效率也略高于其他方法,虽然Ma0=0.2 时由于刚性并不是很大,加速收敛的效果比Ma0更低时明显,但最终的残差均小于其他预处理法,这说明本文格式在保证精度的同时,拥有更良好的稳定性. 图12 Ma0=0.05 时流场的等Mach 线 (a) 精确解;(b) Weiss &Smith;(c) Pletcher &Chen;(d) 本文方法Fig.12.Mach contour of the two-dimensional bump flow problem,Ma0=0.05:(a) Exact solution;(b) Weiss &Smith;(c) Pletcher &Chen;(d) the new method in this paper. 针对低速流动问题,本文基于虚拟压缩法的思想,提出一种以当地Mach 数、来流Mach 数、密度、温度、每个维度的分速度和Reynolds 数为变量的预处理矩阵,相比Weiss,Choi,Dailey,Pletcher和Turkle 等提出的矩阵,把控制方程的刚性在Ma<0.5 时进一步降低到1 左右,使得特征根之间的量级差异进一步减小,从而提升了求解效率,同时改进了从预处理到关闭预处理的过渡不够光滑的不足. 展开数值实验验证了新方法的可靠性.通过一维算例验证了新方法的准确性,将预处理和不处理的结果加以对比,证明了预处理方法可加速计算低速流动问题的收敛.通过平板层流边界层和黏性方腔流动问题进一步验证了本文方法在二维低速流动问题中可以获得高精度数值解,并且拥有更高效的收敛性,随着黏性作用越强,这种高效性越明显.通过二维鼓包管道流动问题,验证了本文方法在曲线坐标系下仍能保持良好的精度和收敛性,而且具备更好的稳定性.目前本文重点在于改进算法,故选取算例的结构比较简单,未来将会尝试模拟复杂网格,非定常流动或引入湍流模型. 感谢中国科学院力学研究所高温气体动力学国家重点实验室的李诗尧博士,天津大学水利工程仿真与安全国家重点实验室的陈嘉禹硕士为本文提供的计算资源;感谢天津大学数学学院2018 级程启豪同学,南开大学数学学院学习部2018 级左晨琛、2019 级的戚红利、2020 级赵振岐等同学为本文的矩阵特征系统在曲线坐标系下数学性质以及特定几何结构从笛卡尔坐标系下到曲线坐标下变换涉及的复分析和拓扑问题的讨论;感谢国防科技大学空天科学学院田正雨教授,南京航空航天大学航空学院陈红全教授,南京航空航天大学数学系张燕博士为本文提出建议.3.3 新预处理矩阵的提出
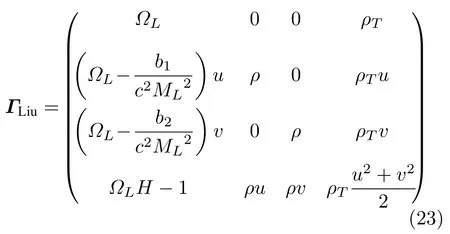
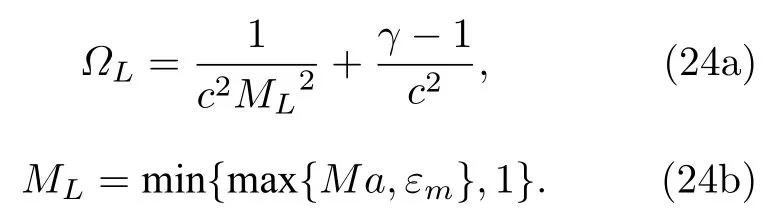
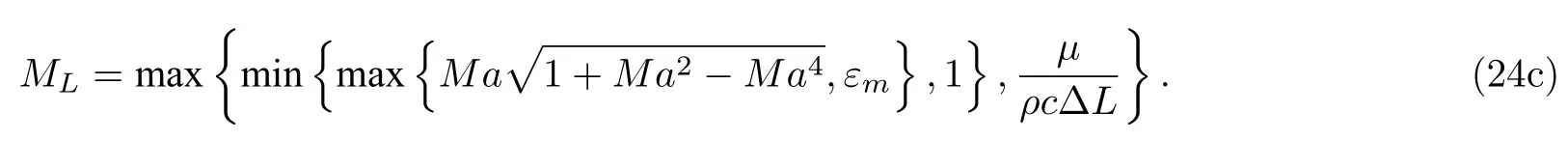

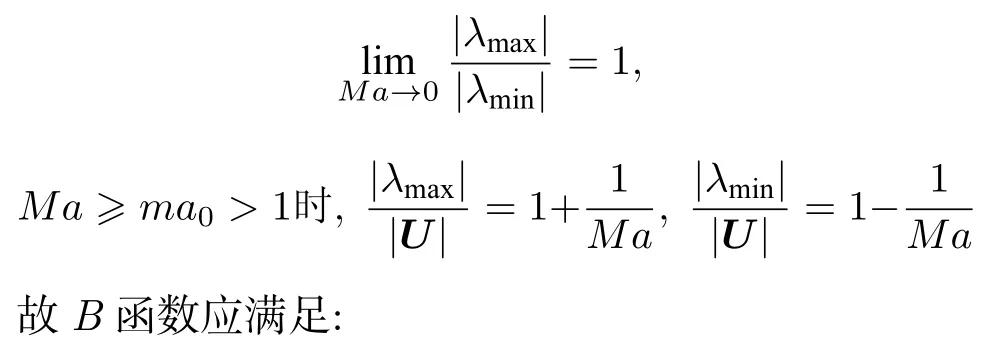
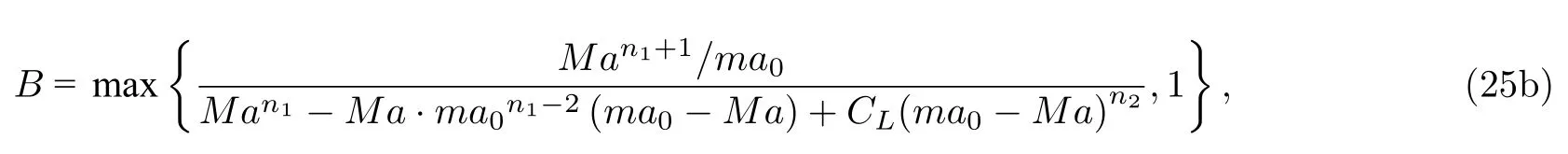
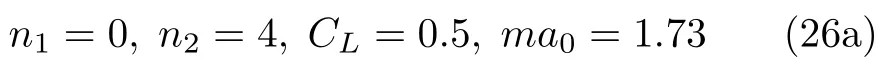

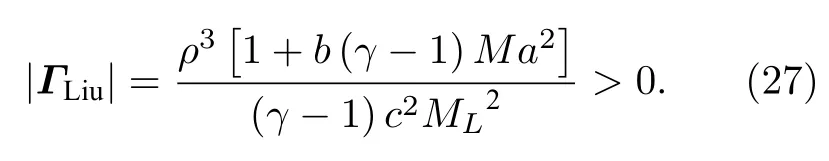
3.4 经新预处理法后的特征系统

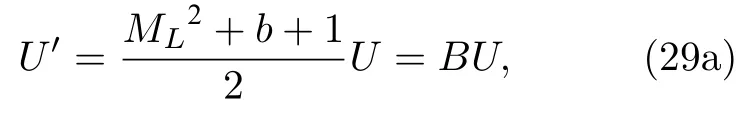
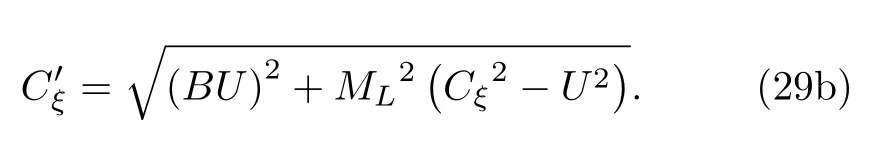
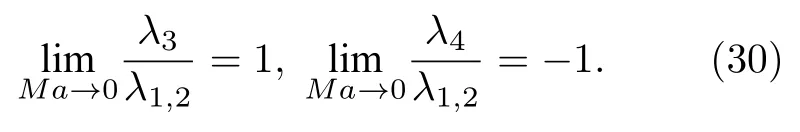
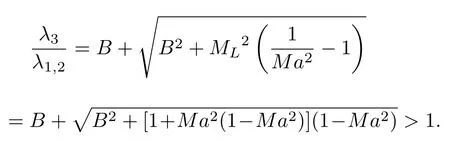
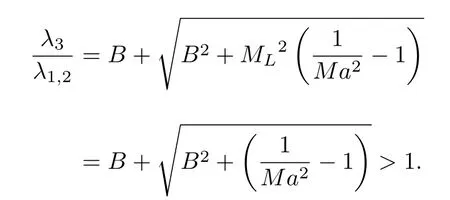
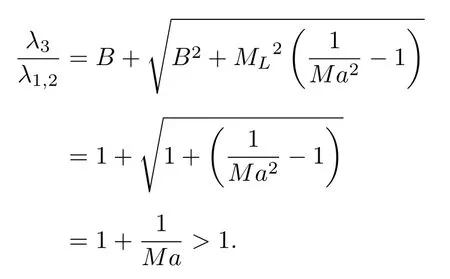
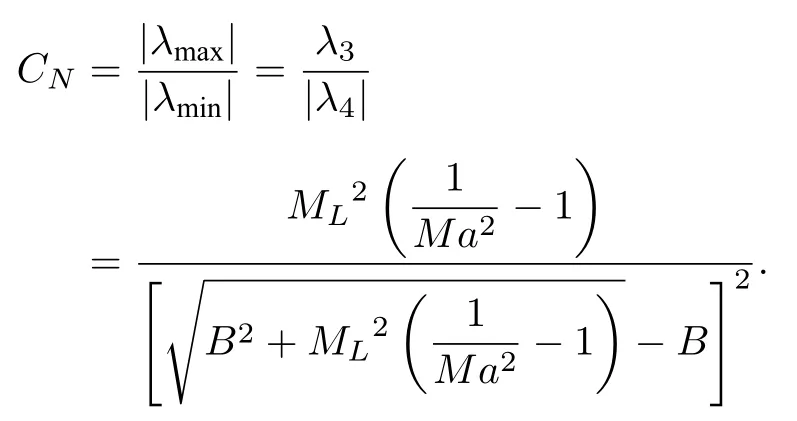
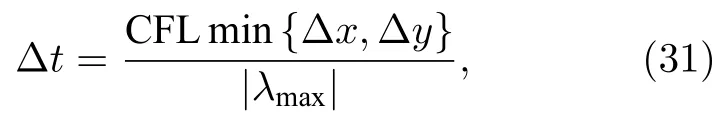

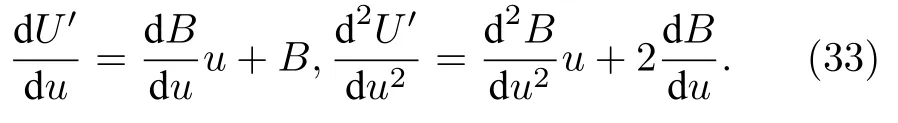
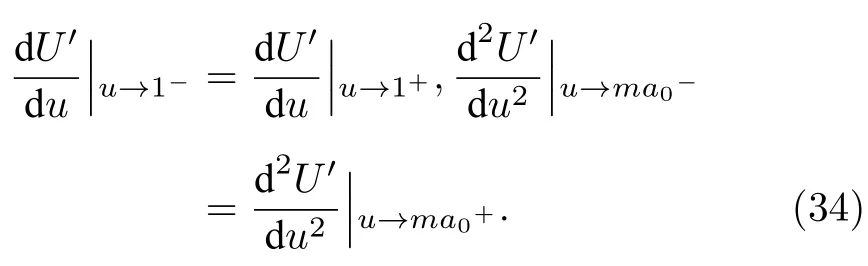
4 数值求解
4.1 空间离散
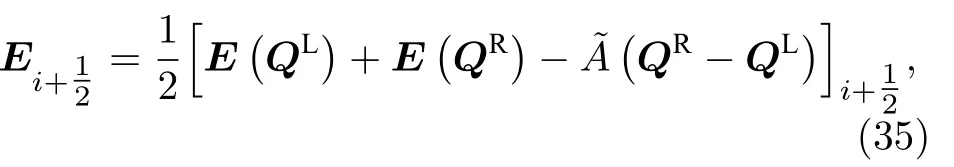
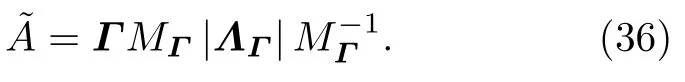
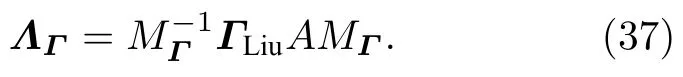
4.2 时间推进

4.3 非定常问题的时间推进
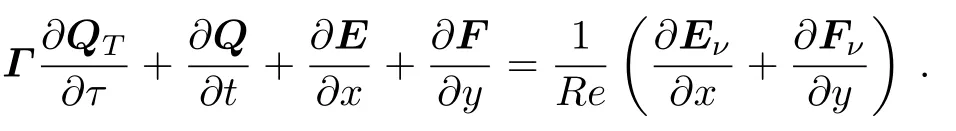
5 数值模拟验证
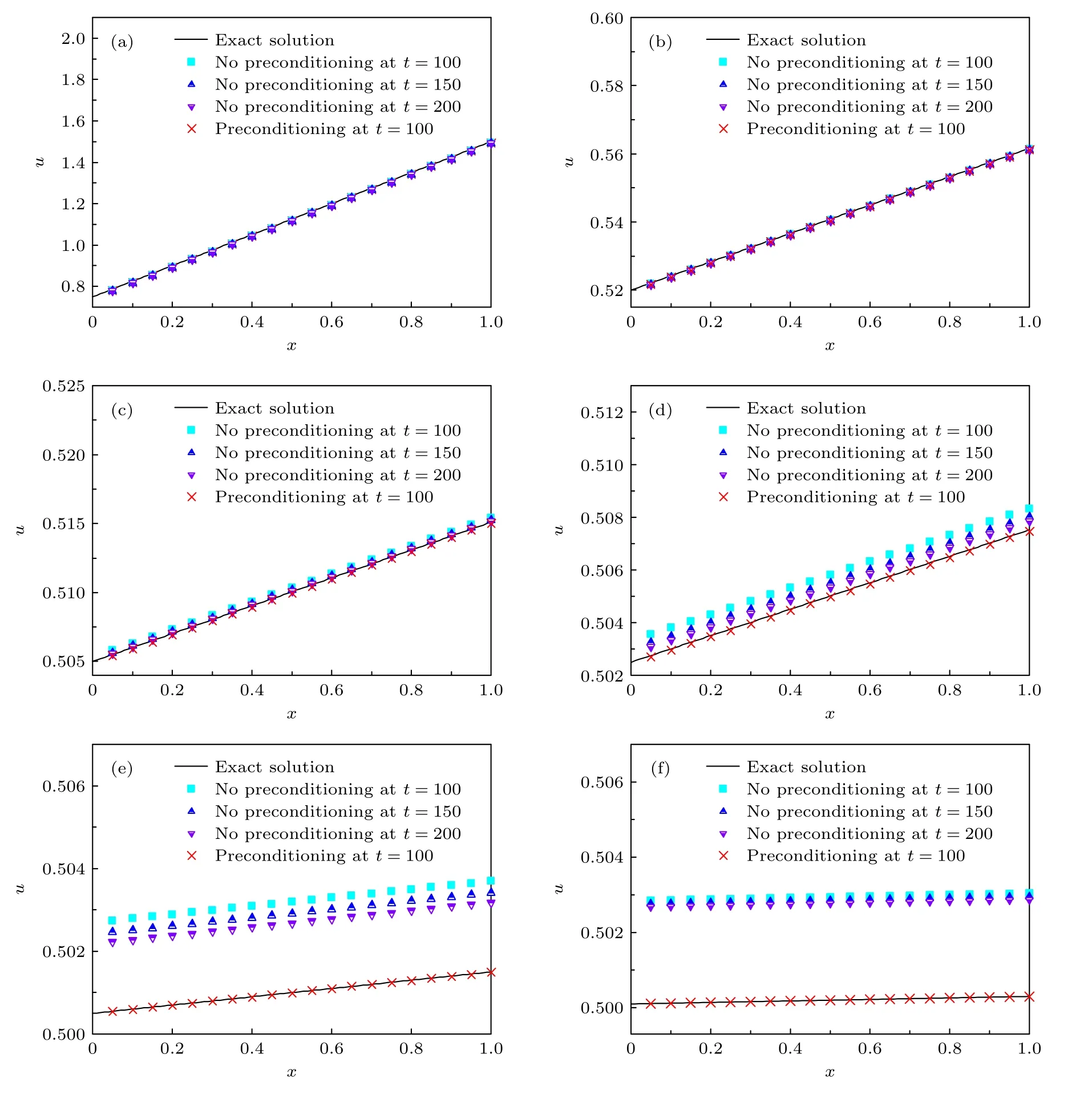
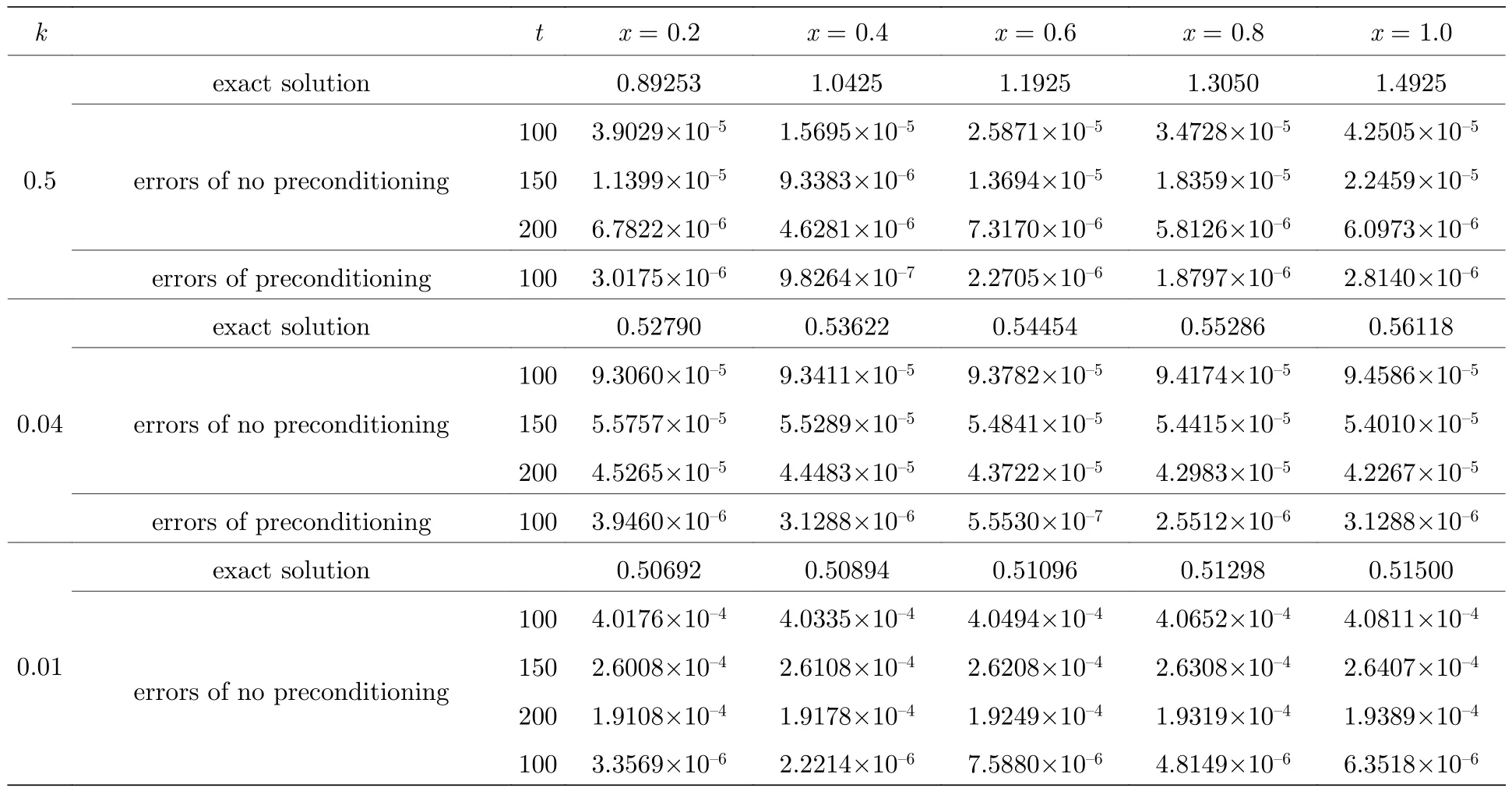
5.1 精度测试
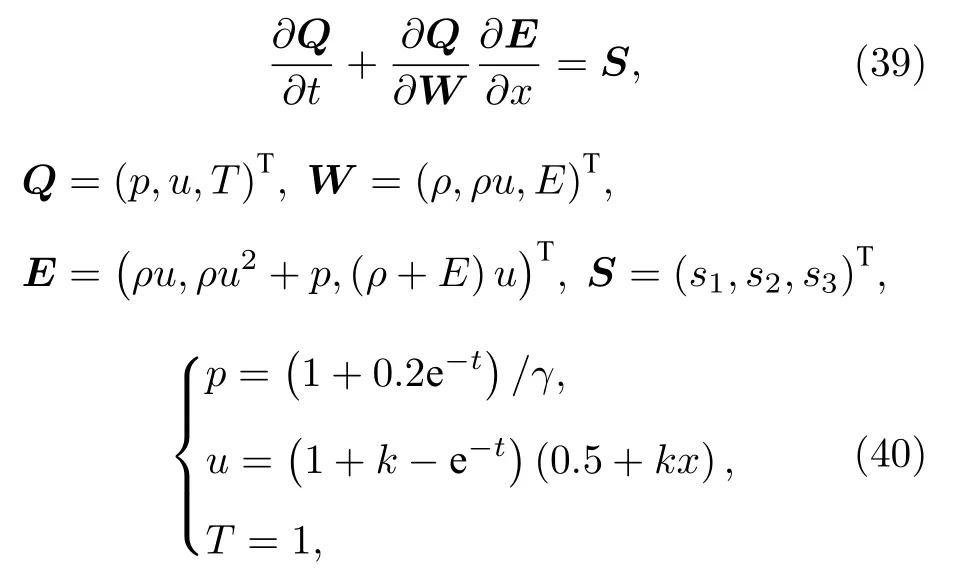
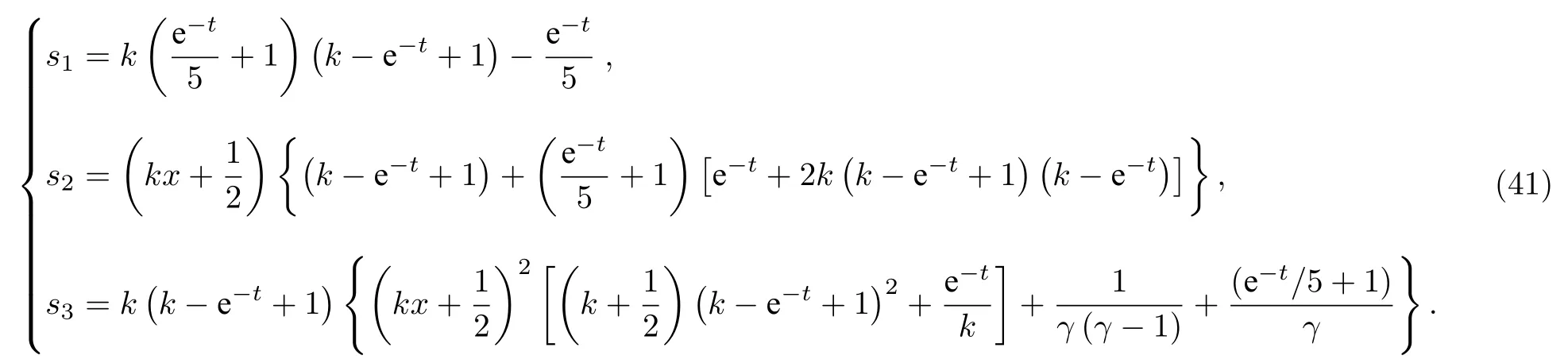
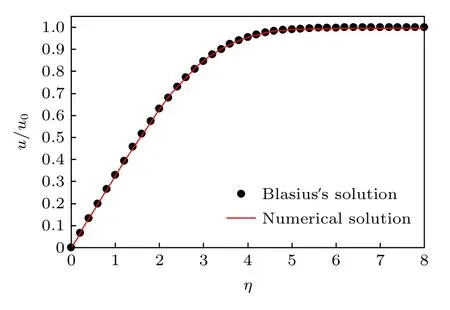
5.2 平板层流边界层
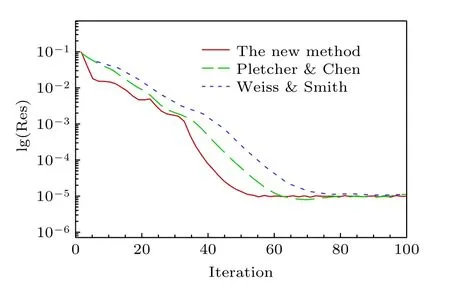
5.3 空腔顶盖驱动
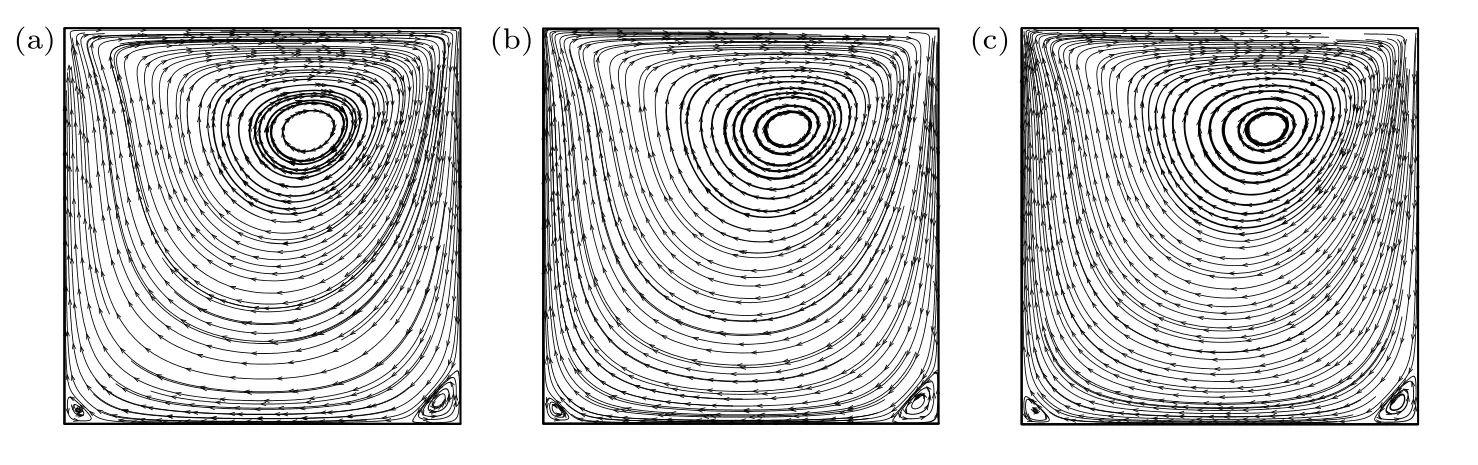
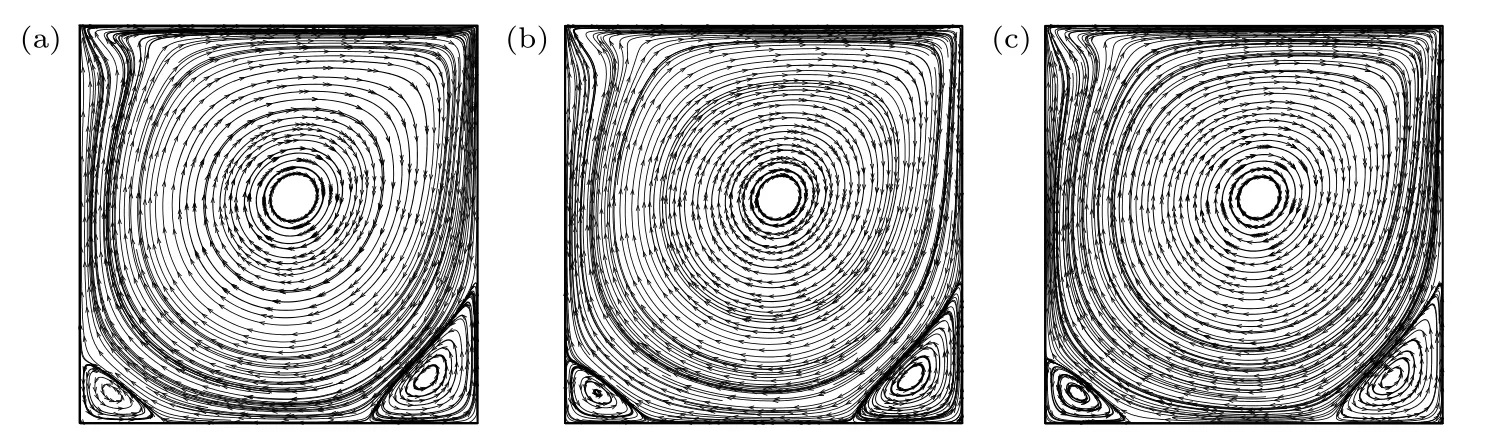
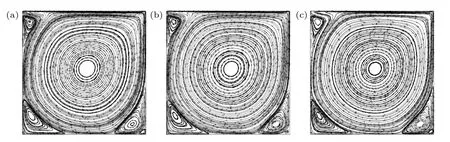
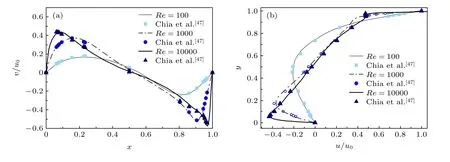
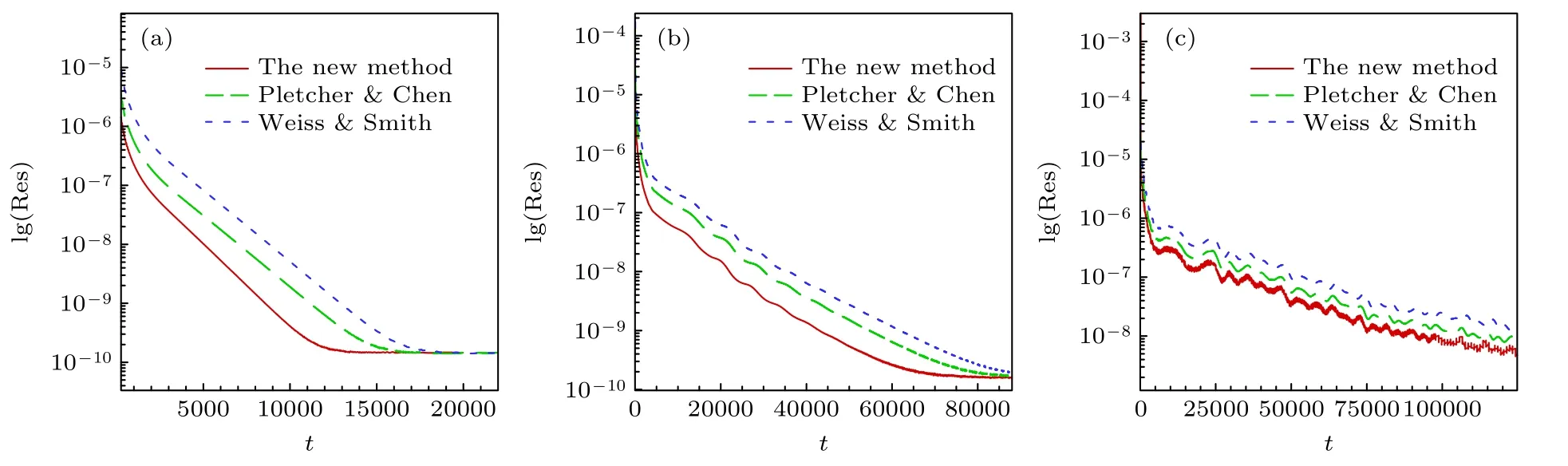
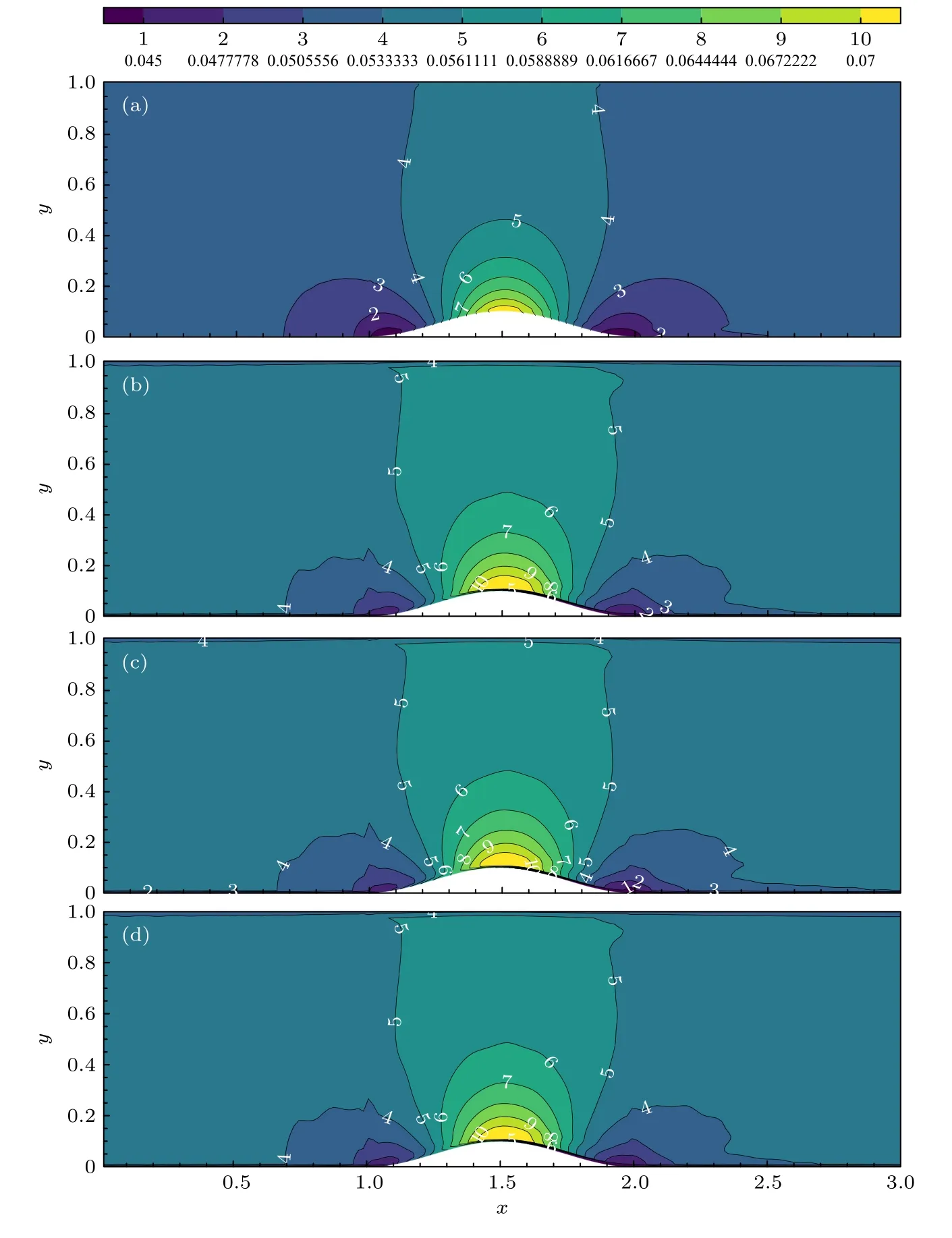
5.4 带凸鼓包的二维管道流动
6 结论
