低维材料物性的非均匀应变调控*

王娅巽 郭迪 李建高 张东波

(北京师范大学核科学与技术学院,北京 100875)

探索低维材料的新奇物性是当前凝聚态物理和材料科学基础研究的一个重要前沿.应变是调控低维材料物性的一个重要手段.相比于块体材料,低维材料通常具有良好的力学柔韧性,并表现出敏锐的结构-电子响应关系,因此可以通过结构变形对材料电子性质进行有效调控.本文主要目的是介绍二维材料中通过非均匀应变获得新奇物性的研究进展.主要讨论两个效应,即赝磁场效应和挠曲电效应.具体来说,通过解析理论、实验进展、计算模拟以及围绕这些效应的应用等方面介绍相关研究进展.从计算模拟的角度看,由于非均匀应变破坏了晶体的平移对称性,基于周期性边界条件的量子力学计算方法如第一性原理不再适用.本文将介绍一个专门用来模拟非均匀应变的原子级计算方法,即广义布洛赫方法,并简要介绍该方法的一些具体应用.

1 引言

二维材料指仅具有单原子或数个原子厚度的层状结构.在层内,原子间通过较强的共价键连接;而在层间,原子间仅存在较弱的范德瓦耳斯作用.因此,电子的运动被限制在一个二维的超薄通道之中.这种特殊的物质组织方式赋予二维材料许多新奇物性,是当前物理、化学、材料等学科基础研究的重要研究对象.二维材料种类非常繁多,包括金属如石墨烯体系[1,2],半导体如过渡金属硫化物[3−5],绝缘体系如六角硼氮体系[6,7],以及二维磁性体系[8]等.由于层间较弱的范德瓦耳斯作用,多层二维材料中不同层之间由于晶格失配带来的对结构与电子性质的影响比较微弱,因此二维材料普遍具有很好的可堆垛性[9,10].对应的范德瓦耳斯异质结构(比如双层以及多层的扭转结构)相比于单层结构,具有更为复杂也更为独特的电子性质[11−13].由于二维材料相比于块体材料优越的物理化学性质,以及近期在大规模可控合成方面的进展,它们在新一代电子器件设计如数据存储[14,15]、集成电路[16]、柔性电子[17]等方面的应用也非常有前景.

作为层状结构,二维材料普遍具有超常的力学柔韧性,体现在两个维度上.在面外,由于仅具有单原子或数个原子的厚度,二维材料容易发生面外的结构变形.比如仅有温度的扰动就可以引起石墨烯自发的结构翘曲变形[18].这是因为,面外变形对二维材料面内的原子之间的强共价化学键的影响很小,从而具有较小弯曲模量.在面内,大多数二维材料也具有超常的力学柔韧性[19,20].实验和理论均证明石墨烯可以承受高达25%的弹性应变[21],远高于相应的块体材料金刚石所能承受的弹性应变.这些优良的力学柔韧性,以及二维材料具有的灵敏的电子性质-应变相应关系,使得通过应变调制材料电子性质成为可能,并已形成了一个专门领域,即应变工程[22,23].

的确,通过应变可以有效调控材料的物性.比如,简单的单轴应变(拉伸或压缩)可以大范围地改变材料的电子能带结构如能隙,从而实现对电子导电性以及其他相关物理性质的有效调控.应变对材料的声子性质也有显著影响,可以显著改变声子色散谱,从而对材料热力学以及热输运产生重要影响.从实际角度看(如实验以及各类应用),二维材料受到的应变在很多时候是非均匀的,如热扰动、衬底、缺陷等因素造成的结构畸变[24−27].其次,微型器件设计等方面,由二维材料形成的异质结构也会引起结构畸变[28,29].这是因为构成异质结的不同材料之间存在晶格失配,从而导致长程的非均匀应变场.此外,物理和材料研究中,为了获得新奇电子特性,也可以对包括二维材料在内的低维材料施加非均匀结构变形.在这个方面,一个代表性的例子是赝磁场效应[30].通过非均匀应变诱导电子态发生朗道量子化,其运动由巡游性转变为局域化,其能量按照朗道能谱分布.这样得到的赝磁场强度常常要远强于实验室能够实现的磁场强度.

二维材料中非均匀应变调控物性的研究涉及多个前沿领域,其中赝磁场效应和挠曲电效应是两个重要方向.赝磁场指非均匀应变诱导的朗道量子化;挠曲电是指非均匀应变下材料中产生的沿应变梯度方向上的电极化.在非均匀应变物性调控的研究中,主要的手段包括解析理论、实验研究和计算模拟,本文将从这3 个方面介绍赝磁场和挠曲电方面的研究进展.在最后一部分,还将基于课题组的研究进展,简要介绍一个适用于非均匀应变研究的计算方法,即广义布洛赫方法.

2 赝磁场效应

由于只有原子尺度的厚度,二维材料如石墨烯在受到外部影响时容易发生非均匀的结构变形.以石墨烯为例,缺陷、温度扰动[31−34]或者衬底的粗糙度[33,35,36],都可以造成二维结构的翘曲变形.由于非均匀应变的影响,石墨烯电子发生类似磁场效应的朗道量子化,称为赝磁场效应.物理上,赝磁场效应可以通过规范场来阐述[34,37−39].具体来说,非均匀应变使得两个狄拉克点K和K'沿着相反方向移动,并产生局域矢量势,即导致赝磁场的产生.在石墨烯的两个谷中,赝磁场具有相反的符号,这也就意味着赝磁场并没有破坏石墨烯晶格的时间反演对称性.

赝磁场效应的发现引起人们对非均匀应变调制电子性质的广泛关注.研究人员发现赝磁场可以有效充当超过10 T 的均匀磁场[40,41].甚至有研究报道在石墨烯中可以获得高达1000 T 的赝磁场[42].此外,赝磁场不仅存在于石墨烯中,也存在于其他蜂窝晶格结构的材料中,如二维过渡金属二硫族化合物(MX2)[43,44].接下来,本文将从理论模型、计算模拟、实验观测和应用这4 个方面来介绍赝磁场效应的研究内容与进展.

2.1 理论模型

在单层石墨烯中[45],通过考虑声子-电子相互作用,可以推导出弹性应变下对应的赝磁场形式.在受到应变作用后,石墨烯K点附近的电子态呈现出无质量狄拉克费米子特征,其哈密顿量为

式中,ℏ 是约化普朗克常数,大小为h/(2π);σ为泡利矩阵;υF为电子的费米速度;∇是梯度算符;矢量A的分量表示为

其中t1,t2,t3是碳原子与3 个近邻之间的电子跃迁参数(hopping),根据文献[44],当原子位移比晶格常数小的时候,有

这里,a是晶格常数;t是无应变情况下的最近邻跳跃参数,单位为eV;ρl是l方向上的电阻率;β为电子Grüneisen 参数:

在连续极限下,有

其中u(r) 表征石墨烯中形变所产生的原子位移.由此,可以得到赝磁场的矢量A:

其中,uxx,uyy和uxy代表3 个不同方向上的应变张量,c是一个数值因子,可令c=1.赝磁场的强度大小即为

上述过程得到的矢量A是对于石墨烯的K谷来说的,对于另一个谷K',得到的结果则与(6)式的符号相反,这符合时间反演不变性的要求.

根据连续模型,研究表明沿3 个主要晶体学方向排列来设计应变能够得到赝磁场[45],正如(6)式和(7)式所展现的,让uxx,uyy与uxy这3 个参数分别取为3 个主要晶体学方向上的应变场,那么就能得到能够调控的赝磁场矢量,从而得到具有相应强度的赝磁场.

2.2 计算模拟

石墨烯中赝磁场效应首先被原子级计算证实.2010 年,Guinea 等[45]设计三角形对称性应变模拟得到一个10 T 左右的均匀赝磁场,通过设计应变产生的赝磁场有可能观察到类似量子霍尔效应(QHE)的现象.Guinea 等设计的应变通过沿着[001],[010],[100]这3 个等效的晶体方向进行拉伸与压缩来得到,施加在这3 个主要方向上的力会分布在整个石墨烯晶格中,从而在石墨烯中产生非均匀应变.发生非均匀应变的石墨烯中产生了一个中心均匀分布的赝磁场,引发电子的朗道量子化,产生朗道能级.Guinea 等的研究还表明,石墨烯的能带结构在他们设计的应变下受到了调控,使通过非均匀应变诱导的赝磁场打开能带带隙成为可能.同年,Low 和Guinea[46]利用面内弯曲应变对非均匀应变在石墨烯中诱导出的赝磁场进行了研究,同样证实了非均匀应变在石墨烯中引发的赝磁场效应.Low 和Guinea 利用应变调控得到了9 T 强度的赝磁场,其面内应变的几何示意图如图1 所示,他们分析了石墨烯在9 T 实际外加磁场与应变诱导出9 T 赝磁场情况下的典型能量色散随动量沿输运方向的变化,结果如图2 所示.

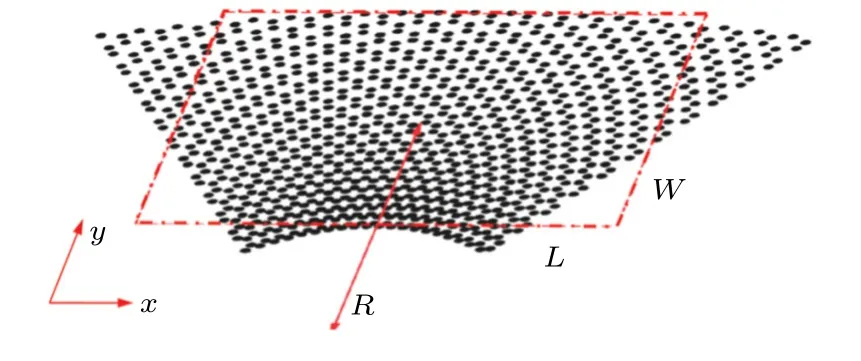
图1 最大应变为50%的应变几何示意图[46]Fig.1.Sketch of an example strain geometry with a maximum strain of 50%[46].

图2 在(a)实际磁场B=9 T,(b)赝磁场Bs=9 T 情况下,典型能量色散随动量沿输运方向的变化[46]Fig.2.Plot of typical energy dispersion as a function of momentum along the transport direction for the case of (a)real magnetic field B=9 T,(b) pseudomagnetic field Bs=9 T[46].

Abedpour 等[47]对赝磁场强度与褶皱形状的关系进行了理论探索,他们以环形石墨烯为研究对象,选取剪切形变作为应变,从连续介质弹性理论与分子动力学模拟两个方面进行了研究并计算诱导出的赝磁场强度,发现剪切应变能够使环形石墨烯中出现褶皱,即产生了显著的非均匀应变,诱导出了增强的赝磁场.Zhu 和Li[48]对基板上的纳米颗粒给石墨烯形态带来的影响进行了系统性的分子动力学模拟,石墨烯覆盖于具有纳米颗粒的衬底之上,从而在石墨烯上出现可以调控的褶皱,Zhu和Li 推导出了纳米颗粒临界色散距离与颗粒尺寸的二阶多项关系式,这将有利于在实验中利用纳米颗粒设计出理想的石墨烯褶皱.2012 年,Yamamoto 等[49]研究了基底空间结构对石墨烯形态的影响,他们将石墨烯附在具有二氧化硅纳米颗粒的二氧化硅衬底上,研究单层石墨烯与多层石墨烯结构的演变与纳米颗粒密度之间的关系,并推导出了最大褶皱长度的精确解析表达式,这个结果可用于预测类似研究中能够得到的赝磁场数值的上限.

2.3 赝磁场的实验观测

2010 年,Levy 等通过扫描隧道显微镜(STM)实验证实了应变诱导产生的赝磁场效应[50].在他们的实验中,石墨烯生长完成后,并不是在整个铂(Pt)衬底的表面上均匀存在的,在石墨烯贴片的边缘附近总是会出现一些纳米气泡,有时,贴片的中心或者贴片之间的边界附近也会存在纳米气泡.由于Pt 衬底和石墨烯的膨胀系数之间存在差异,因此石墨烯中的这些纳米气泡也可以通过退火法获得.直接用扫描隧道光谱(STS)测量纳米气泡区域,光谱显示出一系列间隔超过100 meV 的强峰,而这些峰在其他区域的STS 光谱中并没有出现.Levy 等的研究表明,这些峰的分离方式与磁场中的朗道能级相同,这也就意味着,这些峰是由应变产生的赝磁场引起的.赝磁场使得通过施加应变来调控石墨烯的电子特性成为可能.

利用非均匀应变产生的赝磁场的磁场强度比磁体产生的外部磁场的强度更高[51−53],这也是促使研究人员通过实验来验证赝磁场存在的原因之一.Levy 等[50]的实验结果表明,在Pt(111)表面生长的石墨烯中,由于纳米气泡的存在而产生的高度应变诱导出的赝磁场强度超过了300 T,这证实了通过非均匀应变在石墨烯中诱导出的赝磁场强度可以达到数百特斯拉的量级.

近些年来有关赝磁场的实验研究有很多.Jiang等[54]利用纳米颗粒在六方氮化硼衬底上的石墨烯中引入应变,运用扫描隧道光谱进行研究,利用形成的莫尔图案的放大效应实现了局部应变的直接测量,通过赝朗道能级(PLLs)光谱量化了观察到的应变诱导的赝磁场.Hsu 等[55]通过将单层石墨烯放置在他们特定设计的纳米结构上,诱导出了具有理想的空间分布的强赝磁场,高达800 T,通过STM/STS 进行直接测量,证实了应变诱导巨大赝磁场、实现全局谷极化的可能性.Kun 等[56]对皱缩的石墨烯中的赝磁场进行测量,通过共焦拉曼光谱证明应变的波动会带来赝磁场的涨落,从而引起电荷载流子显著的谷内散射.

2.4 赝磁场的应用

2.4.1 Aharonov-Bohm 干涉仪

低维体系的材料尺寸十分小,有时甚至能与电子的相位相干长度处于相近量级,在这种情况下,量子相位干涉现象就成为了研究中需要考虑的内容[57,58].磁场下,磁矢势对电子波函数相位带来影响而产生的量子干涉效应称为Aharonov-Bohm 效应(AB 效应)[59,60].量子力学中,虽然波函数相位不可测量,但相位差能够利用干涉实验测得[61].

Cano 和Paul[62]已经证明,在固定磁场下,沿环路顺时针和逆时针行进的电子会获得不同的相位,导致局域态的Aharonov-Bohm 振荡,即磁场能够通过AB 效应影响电子干涉对局域态密度的贡献.他们的干涉仪原理图如图3 所示,两个杂质与STM 尖端分别位于材料表面上的3 个不同位置,作为3 个顶点构成闭合路径,即散射回路,外加磁场让回路中的材料处于实际磁场中,以(111)Ag表面为例,理论模拟推导得到STM 结果如图4 所示,其中,水平条纹即反映了AB 效应对局域态密度的干涉.Cano 和Paul 的研究结果表明,在磁场使得费米波长比朗道轨道小得多的情况下,利用STM 设备制作纳米尺度上的Aharonov-Bohm 干涉仪是可行的.

图3 STM 干涉仪:r 表示STM 尖端在表面的位置,r1 和r2表示两个杂质[62]Fig.3.STM interferometer:r represents the position of the STM tip on the surface and r1 and r2 represent two impurities[62].

图4 在减去B=0 的信号后,在Ag(111)表面上两个杂质相隔20 nm 的情况下模拟得到的STM 图像[62]Fig.4.Expected STM patterns for two impurities 20 nm apart on the Ag(111) surface after subtraction of the B=0 signal[62].

2011 年,de Juan 等[63]通过形变场诱导出赝磁场效应,并利用赝磁场产生AB 效应,同时,他们提出了一种简单的用STM 设备构成的Aharonov-Bohm 干涉仪.de Juan 等提出的纳米量级上测量AB 干涉的设备原理与Cano 和Paul[62]提出的相似,区别在于,de Juan 等并不外加实际磁场,而是通过在回路中的石墨烯上施加应力使其发生非均匀应变,诱导出赝磁场效应,从而产生AB 干涉.电子的顺时针路径和逆时针路径通过零场的时间反演对称性连接[62,63].de Juan 等推导出态密度关系式为

其中,NA=0表示无形变时的总态密度,Nloop表示在没有形变的情况下所有穿过两个杂质并包围有效区域的散射路径所产生的干涉,Φ表示在这个区域内由形变引起的赝磁场通量.(8)式中余弦的出现是AB 效应产生的体现,证明了弹性应变确实可以产生非零的AB 相.同时,de Juan 等得出结论,固定STM 尖端,通过改变施加的应力调控赝磁场大小,则根据局域态的 cosΦ余弦可以直接测量出局部应力的大小.

2.4.2 调控电子能带结构并构建平带结构

利用应变工程探索具有新型特性的二维原子晶体是低维体系中一个重要的研究方向,Mao 等[64]运用扫描隧道显微镜和光谱学,结合数值模拟,证明了单层石墨烯中能够产生赝磁场,且利用赝磁场效应可以产生平带结构,而平带能够促进强电子相关相的产生[60−67],他们的研究为利用非均匀应变调控二维晶体的电子结构与性质提供了新的途径.

Mao 等[64]以 NbSe2或六方氮化硼(hBN)为衬底,在其之上沉积出单层石墨烯,并通过热诱导产生屈曲应变,从而诱导出具有周期性的赝磁场.他们从两个方面的测量研究来证实在样品中产生了赝磁场:一是用扫描隧道显微镜对 NbSe2衬底上的屈曲石墨烯进行测量,分析并计算出了由赝磁场引起的赝朗道能级中N=0 对应的峰的赝磁场强度;另一个是测量出了N=0 能级中电子波函数的子晶格偏振.利用赝磁场来构建平带的特点是不需要打破时间反演对称性.Mao 等测量了赝磁场下周期为14 nm 的石墨烯超晶格的能带结构与局域态密度,发现在赝磁场效应的影响下,石墨烯能带被重整为一个个分散的能带,能带的宽度反比于赝磁场的强度.随着赝磁场的增强,能带越来越窄,可以预测,在赝磁场强度无限大的时候,会产生平带结构.屈曲结构的形状、周期和对称性等这些参数在实验中可以通过石墨烯制备手段来进行控制,从而控制应变分布,调控赝磁场的强度.

另外,Mao 等[64]还利用赝磁场研究了平带的相关性效应.由于NbSe 衬底上的石墨烯不能将费米能级带入平带,因此他们采用绝缘hBN 层上的石墨烯作为研究对象,施加电压实现应变调控,结果显示,随着栅极电压的增加,样品的dI/dV光谱曲线的最小值逐渐从空穴掺杂过渡到电子掺杂.这一结果表明通过赝磁场效应可以探索并调控平带中的相互作用效应.

2.5 讨论与展望

赝磁场效应的实验研究主要集中于石墨烯体系,而对其他二维材料体系的探索较少.根据连续模型,赝磁场存在的一个关键条件是费米能级附近低能态电子色散具有无质量狄拉克锥的特征.石墨烯正是这样的典型体系.而很多二维体系在费米能级附近的低能态电子是有质量的费米子,锥的特征不明显.然而,连续模型的建立,仅仅考虑低能态电子结构,高能态的电子态对非均匀应变的响应被忽略.此外,连续模型一般采取最近邻近似.但长程作用对电子结构的影响很多场合下是不可忽略的.解决这个问题的一个方案是进行原子级模拟,对二维材料体系进行系统的计算研究.

3 挠曲电效应

近些年来,挠曲电效应作为一种新型的机电耦合机制受到广泛的关注[68−70].它已经被用来实现许多包括挠曲光伏效应在内的重要应用[71−74].挠曲电效应描述的是应变梯度诱导的电极化现象,它与压电效应有着相似之处,曾有研究人员将挠曲电效应视为压电效应的高阶效应[75,76].但挠曲电效应与压电效应又有非常大的不同之处.比如,压电效应只出现于非中心对称的介电材料中,而挠曲电效应则存在于所有电介质中[77];相比于压电效应,挠曲电效应导致的电极化要弱很多[78,79].

挠曲电可以由电极化的本构方程引入[80]:

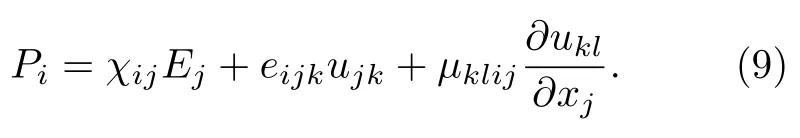
方程的右侧3 项依次表示了介电响应、压电响应与挠曲电响应.其中,χij为介电磁化率,Ej为宏观电场,eijk为压电张量,ujk为应变张量,µklij即为挠曲电张量,它是一个四阶张量,可以定义为

从(9)式可以看出,挠曲电效应强度与应变梯度成正比.在块体材料中,实际可实现的应变梯度的水平通常比较低,因而获得强电极化比较困难.力学上,材料可允许的应变梯度的水平与材料尺寸的大小成反比.因此,采用纳米材料是实现强挠曲电效应的一个重要途径[71,81].低维下,材料通常具有良好的力学柔韧性,同时,它们纳米级别的尺寸允许较大的应变梯度.

3.1 理论模型

对于挠曲电效应的微观机制的描述,可以与压电效应对比[77,82].压电效应指应变诱导的电极化现象.在一个具有反演对称性的介电材料上施加应变,并不能使材料产生电极化,因此,压电效应仅存在于非中心对称体系.但是,当材料经受非均匀应变时,介电材料的对称性在应变梯度方向上被破坏,造成正负电荷中心分离,引起电极化.当然,挠曲电效应的影响因素很多,不仅与材料的应变有关,还与材料的内部结构在应变下的弛豫、缺陷性质等因素相关.一般而言,挠曲电效应主要包含两个方面的来源:电子贡献和晶格贡献[69].

考虑晶格贡献,Tagantsev[80,83,84]利用刚性离子球模型提出了一套挠曲电效应的微观理论,对于有限晶体,平均偶极矩密度的变化可以表示为

其中,Pi是点电荷近似下的有限晶体的平均偶极矩密度,Qn则表示点电荷,Rn,i表示点电荷初始位置的坐标,V与Vfin分别代表样品形变前后的体积.当样品发生形变,第n个原子的位移的第i个组分包含两部分:

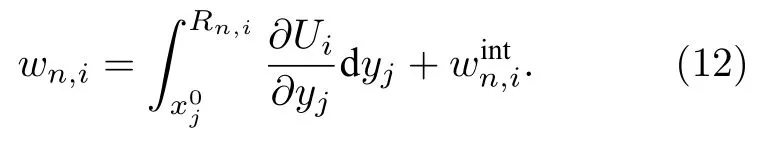
第一项代表外部应变,第二项代表内部应变.应变梯度下,原子位移引发的电荷密度重分布对应挠曲电的电子贡献,而内部位移则对应其晶格贡献[69].内应变来源于晶体的离散性质,通常远小于外应变,在较低的形变限度下,内应变可以被写为应变张量和梯度的线性函数:

式中,H和N分别为应变张量和其梯度的系数因子,与晶体性质相关,在理想晶体中,可以用晶格动力学计算.将(12)式和(13)式代入(11)式得到:

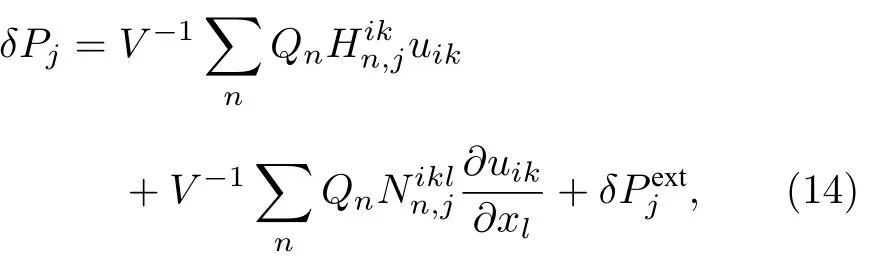
其中,第一项为内应变的压电贡献,第二项为内应变的挠曲电贡献,对应的挠曲电系数即为

(14)式中最后一项的组成较为复杂,它与外应变和体积变化有关,表示表面挠曲电效应.应当提到,这个表面挠曲电效应在理论上存在争议[85].

在类似的理论框架下,电子贡献可以通过一个电荷的连续性模型来表示[86]:

这里,ρ(r) 是应变梯度引起的电子电荷密度变化.

3.2 计算模拟

挠曲电效应微观机制理论模型的建立同时为计算模拟奠定了基础[83,86,87].近年来,挠曲电的计算模拟逐渐增多[78,88−90],尤其是在用第一性原理计算各材料挠曲电系数方面[91−95].对低维材料的挠曲电理论研究也成为了人们关注的重点.近期,Springolo 等[96]利用第一性原理研究了一系列二维材料的挠曲电响应,并提出了一套二维材料中的挠曲电连续性模型.

2008 年,Kalinin 和Meunier[97]以纳米石墨条带、聚乙炔等碳基纳米结构为主,用密度泛函理论对400 个原子组成的低维系统进行计算,得出挠曲电系数量级约为0.1e(就石墨条带而言,若与三维体系对应,则约为0.01 nC/m 量级),并探讨了碳基纳米结构中的强挠曲电效应在机械传感器、纳米机电系统等方面的应用.2019 年,Zhuang 等[98]利用原子模型计算了一系列二维材料的本征挠曲电系数,其构建的材料结构如图5 所示,他们采用弯曲模型来消除压电对总极化的贡献,以MoS2为例,其原子构型如图6 所示,他们发现在计算的石墨烯及其同质异形物、氮化物、IV 族类石墨烯材料、过渡金属双卤代烷(TMDCs)等二维材料中,TMDCs材料具有最大的挠曲电系数.2021 年,Kumar 等[99]用第一性原理计算了单层膜面外弯曲下的横向挠曲电系数,他们发现,挠曲电效应与单层膜的厚度、弯曲方向的弹性模量、组分原子极化率的总和这些因素有着正相关性.同年,Codony 等[95]从第一性原理出发推导了计算纳米结构有限形变下横向挠曲电系数的公式,并运用密度泛函理论计算了C,Si,Ge,Sn 单层结构的横向挠曲电系数,结果如表1 所列.

图5 研究材料的结构 (a)石墨烯同素异形体;(b)氮化物XN,X=B,Al,Ga;(c) IV 族 元素X,X=Si,Ge,Sn 的石墨烯类似物;(d)过渡金属二硫族化合物XS2,X=Cr,Mo,W.(a)—(c)中,h 为屈曲高度,(d)中,h1 和h2 为层内距离[98]Fig.5.Structures of the studied materials:(a) Graphene allotropes;(b) nitrides XN,X=B,Al,Ga;(c) graphene analogues of group-IV elements X,X=Si,Ge,Sn;(d) transition metal dichalcogenides XS2,X= Cr,Mo,W. For(a)–(c),h refers to the buckling height,while in (d),h1 and h2 refer to intralayer distances[98].

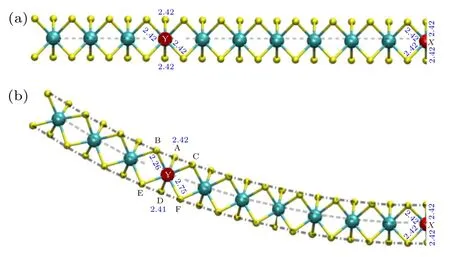
图6 MoS2 片的(a)未形变与(b)形变下的原子构型[98]Fig.6.Atomic configurations of MoS2 sheet under (a) undeformed and (b) deformed[98].

表1 IV 族原子单层膜的横向挠曲电系数µT[e] [95]Table 1. Transversal flexoelectric coefficient µT[e]for group IV atomic monolayers[95].

3.3 实验研究

实验中测量挠曲电效应时,通常要考虑到挠曲电系数的具体分量[81,82],常用的测量方法主要有两种,悬臂弯曲法测量横向挠曲电系数(如图7 所示[100]),金字塔压缩法测量纵向挠曲电系数[77].而对于低维情况,实验研究则相对较少,这是由于以实验手段在一维或者二维材料中实现大应变梯度时测量出由挠曲电引发的电学响应较为困难.低维体系的实验相关测量以悬臂弯曲法为主.

图7 弯曲悬臂梁中的挠曲电极化[100]Fig.7.Flexoelectric polarization induced in a cantilever beam under bending[100].

最近,有报道提出莫尔超晶格中存在挠曲电效应贡献的极化响应[101].Li 等[102]利用扭转下的两个双层石墨烯构成莫尔超晶格并进行了研究,他们通过对上层双层石墨烯施加横向应力,让上层双层石墨烯与下层双层石墨烯之间存在扭转角度,两个双层石墨烯之间的排列方式与原子结构发生变化,最终以ABAB,ABBC 和ABCA 这三种原子堆垛方式为主.Li 等首先用密度泛函理论和有限元模拟计算了莫尔超晶格内的应变梯度与挠曲电极化,发现在以ABAB 形式堆叠区域和以ABCA 形式堆叠区域的交界区,即畴壁区,由于堆垛方式的转变而产生了本征应变,且具有应变梯度,两种堆垛区域附近则出现极化且极化方向相反;而后,他们用侧向压电力显微镜(LPFM)进行了实验测量,通过对测得的本征挠曲电响应做矢量分析,发现所得结果与理论预测的LPFM 相位、幅值分布一致.

挠曲电效应在较小尺寸下的增强也是一个有意义的实验研究内容.Kwon 等[103]采用微米级钛酸锶钡制成多层结构,运用悬臂弯曲法测量了其尺寸效应下增大的横向挠曲电系数,他们发现,相比于单层结构,多层结构显示出了输出电荷的增强.

3.4 挠曲电的应用

3.4.1 挠曲光伏效应

研究发现,利用挠曲电效应可以调控半导体的光伏效应,这为增强现有的光伏器件性能以及制造新型的光伏器件提供了理论支持与新的思路.20 世纪70 年代以来,人们在一些非中心对称的铁电材料中发现了特殊的光伏效应,即铁电光伏效应,也称为体光伏效应,这种光伏效应在理论上不受肖克利-奎伊瑟极限的限制[104−107].2018 年,Yang 等[72]则提出,利用挠曲电效应,可以在任何半导体中诱导出类似的铁电光伏现象.他们的实验发现,具有中心对称的半导体,在具有较大应变梯度时,光电流将出现增强,光电流密度将得到极大增加.Yang等认为,在中心对称的半导体中引发挠曲电效应时,应变梯度引起了质心对称性的破缺,半导体内部极化促进了电荷分离,他们将这种挠曲电效应诱导出的类铁电光伏效应称为挠曲光伏效应.

2021 年,Jiang 等[108]在二维材料中研究了挠曲光伏效应,他们以MoS2为研究对象,通过相变材料VO2引入应变梯度,MoS2的尺寸大于VO2,MoS2一部分直接置于衬底上,一部分则置于放置在衬底上的条形VO2上,这样,条形VO2两侧区域的MoS2将具有不小的应变梯度,同时,通过控制温度来调控相变材料的结构相变可以控制应变梯度的大小.Jiang 等[108]通过扫描光电流显微镜测量发现,在532 nm 的光照下,VO2两侧接触的MoS2,即具有显著应变梯度的区域,相较于其他区域产生了明显增强的光电流.在室温下研究MoS2的电流-电压曲线发现,在具有应变梯度的区域,可以观察到较大的短路光电流与开路光电压,这标志着应变梯度在二维材料MoS2中诱导出了挠曲光伏效应.此外,Jiang 等还进一步测量了在不同温度下的情况,结果表明,当VO2由于温度的改变发生相变而晶格常数增大,MoS2的应变梯度增大时,光生电流将会增强,这说明挠曲光伏效应的光生电流会随着应变梯度的增强而增强.

另外,Artyukhov 等[109]通过第一性原理计算,研究了挠曲电效应对碳纳米管的光学和电学性能的影响,结果表明,在双壁纳米管中,挠曲电效应会导致电子发生跨层的带隙跃迁,这一现象也将有利于增强光伏效应中的电荷分离.

3.4.2 纳米发电机

在不使用电池的情况下,将振动能有效地转化为电能并为纳米机电系统提供动力,是一个十分重要的研究课题.在这方面,压电纳米发电机成为了人们关注的重点.近些年,随着挠曲电效应受到学术界的广泛关注,人们开始将挠曲电效应与压电效应结合起来进行纳米发电机的研究.由于挠曲电效应与应变梯度直接相关,在纳米量级或者低维情况下,挠曲电效应可能会十分显著,有时甚至超过压电性,为纳米发电机的工作效率带来极大提升[74].Qi 等[110]利用压电陶瓷的纳米薄带进行纳米机电研究,报道了薄带在波状或者弯曲情况下由挠曲电效应增强的压电响应,与没有挠曲电贡献的薄带相比,压电响应提高了70%.

目前,对纯挠曲电纳米发电机的研究不多,且实验研究通常是在微米或者几百纳米的系统中进行的.关于低维情况,挠曲电对纳米发电机的影响相关研究主要在于计算模拟与理论解析方面.Wang 等[111,112]提出了具有挠曲电效应的纳米级压电发电机的解析模型,他们的理论研究表明,在构建的发电机模型具有极小的厚度时,挠曲电效应所产生的电压输出和功率输出会高于压电效应所带来的电压输出和功率输出.

挠曲电纳米发电技术的发展,提供了一种获取能源的新的途径,在一些具有特定结构的纳米发电系统中,与压电纳米发电相比,挠曲电效应能带来更高的发电性能.由于压电效应要求材料具有非中心对称性,而挠曲电效应不受限于材料对称性,所以挠曲电效应也为纳米发电机材料的选择提供了更多的可能性.

3.5 讨论与展望

挠曲电效应作为近些年才受到广泛关注的新型机电耦合,其研究方法还有着许多需要完善的地方.关于挠曲电效应的一些具体理论还存在着争议,如表面挠曲电效应是否存在,挠曲电效应的具体物理机理,这些都还需要进一步的研究与讨论.对于低维体系,挠曲电效应研究的不足之处主要在于实验方面的研究很少,也还没有发现挠曲电系数能与BaTiO3这类铁电材料相比的低维材料,研究宏观材料各个挠曲电分量所使用的实验方法无法直接应用于低维材料,而在低维体系中准确调控出较大的应变梯度具有不小的难度,近些年对于挠曲电效应的研究中,关于低维材料尤其是二维材料的挠曲电实验研究及其应用的探讨是匮乏的.

4 广义布洛赫方法

4.1 计算方法

理论计算是研究低维材料电子性质的重要手段.多数情况下,利用材料的晶体平移对称,只对材料原胞进行计算模拟即可探讨相应性质,常见的计算方法如第一性原理计算[113,114]、密度泛函紧束缚[115,116]等在计算中仅需要考虑少量原子.但是,在非均匀应变的情况下,由于晶体平移对称消失,常规计算方法不再适用.

力学上,低维体系的基本形变包含三种类型:拉伸与压缩、弯曲和扭曲.若是考虑二维材料,弯曲形变存在面内弯曲与面外弯曲两种情况.面内弯曲、面外弯曲和扭曲形变,都将在低维材料中引入非均匀应变,打破材料的平移对称性.此时,如果想要用第一性原理等常用方法进行严格的理论计算,则需要采用足够大的晶胞,涉及到的原子数量较大,有时甚至需要将整个材料的所有原子都纳入计算范围中[117],这显然在计算资源以及时间成本的花费上极不划算.

广义布洛赫方法在布洛赫定理的基础上将旋转对称性与螺旋对称性引入计算中.从而在基本的非均匀结构变形中(如弯曲、扭曲),能够以较少的原子进行精确计算,保证精度的同时极大地减少了计算量.对于非均匀应变下的低维材料,广义布洛赫方法能够进行结构优化、能带与电子声子性质的计算、分子动力学模拟等一系列计算研究.

考虑扭曲体系,以扭曲的G/hBN 横向异质结这一低维体系为例,如图8 所示,定义一个沿着扭曲轴的螺旋操作[118]:

图8 (a)扭曲形变下的G/hBN 横向异质结与(b) 其未应变情况[118]Fig.8.The G/hBN lateral heterojunction (a) under twisting deformation and (b) its unstrained state[118].

其中,T为平移分量,Ω为转动分量的转动角度.那么,扭曲形变下的结构可以被描述为

其中,X0,n是初始原胞中第n个原子的位矢,Xλ,n即是执行了λ次螺旋操作后得到的原胞内第n个原子的位矢.此时,广义布洛赫波函数写为

其中,φn,α(r) 表示第n个原子的α轨道的原子波函数,Sλφn,α(r) 则表示螺旋对称匹配下相应的原子轨道[119−121],exp(iκλ)为螺旋操作的本征值,κ是螺旋量子数,其范围为−π ≤κ<π,ζ为允许的螺旋操作的次数.

对于弯曲体系,以弯曲的石墨烯为例,如图9所示,定义一个沿着曲率方向的旋转操作[118]:

图9 (a)弯曲形变下的石墨烯与(b)其未应变情况[118]Fig.9.Graphene (a) under bending deformation and (b) its unstrained state[118].

其中,Ω为旋转角度.那么弯曲形变下的结构可以被描述为

式中,R为旋转矢量,T1为平移矢量,X0,0,n是初始原胞中第n个原子的位矢,Xλ1,λ2,n即是执行了λ1 次平移操作与λ2 次旋转操作后得到的原胞内第n个原子的位矢.此时的广义布洛赫波函数可以写为

其中,φn,α(r) 同样表示第n个原子的α轨道的原子波函数,而表示旋转和平移对称匹配下相应的原子轨道,相位因子exp(ikλ1+iκλ2)由旋转算符和平移算符的特征值组成,κ为旋转量子数,−π ≤κ<π,k为波矢,ζ1是允许平移的次数,ζ2是允许旋转的次数,有ζ2Ω2π,λ20,1,2,···,ζ2−1.

如果同时考虑螺旋对称性与旋转对称性,而平移操作又相当于一种特殊的螺旋操作,则可以得到广义布洛赫方法描述晶体结构的统一表达式[122]:

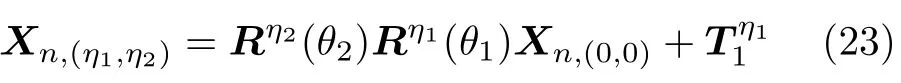
广义布洛赫波函数则写为[118,123]

其中,Oαα′即是相应的对称操作.

在程序的实现上,广义布洛赫方法的建立可以修改已有的基于标准布洛赫定理的计算程序,如基于密度泛函的紧束缚计算方法[124,125].

4.2 计算实例

广义布洛赫方法在计算中没有引入新的近似,所以其计算精确度由选用的理论模型来决定,将基于密度泛函的紧束缚理论与广义布洛赫方法相结合,可以研究各类非均匀应变下低维材料的电子性质.

运用广义布洛赫方法,我们证明扭曲的石墨烯条带中非均匀应变能够诱导出赝磁场效应.考虑石墨烯条带的扭曲变形.图10 和图11 分别给出了170 nm 宽zigzag 型 和176 nm 宽armchair 型 石墨烯纳米条带未形变和扭曲形变下的能带结构及对应的态密度[126].zigzag 型石墨烯条带扭曲率为0.61(°)/nm,armchair 型扭曲率为0.66(°)/nm.尽管有理论预测显示扭曲并不是朗道量子化的理想选择[30,45,127,128],但广义布洛赫方法的计算结果表明,无论是哪种结构的石墨烯条带,在扭曲应变下诱导出的赝磁场都能引发电子的朗道量子化,产生定义良好的朗道谱,正如图10 和图11 的态密度图中垂直虚线所示.这一结果既说明了原子量级的计算模拟的重要性,印证了低维材料中赝磁场效应的应用,也为计算非均匀应变下的低维材料电子性质提供了新的思路.

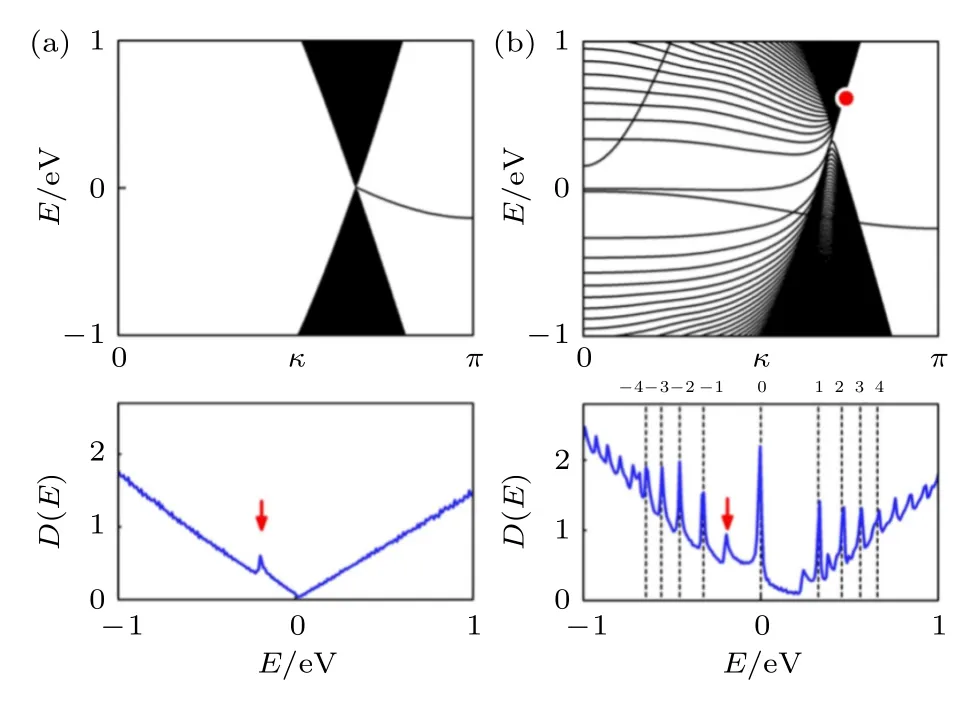
图10 170 nm 宽zigzag 型石墨烯条带在未应变(a)与0.61(°)/nm 扭曲率(b)下的能带结构(上图)和态密度(下图)[126]Fig.10.Band structures (upper) and density of states(lower) of a 170 nm wide zigzag graphene nanoribbon at(a) no strain and (b) twist rate=0.61(°)/nm[126].

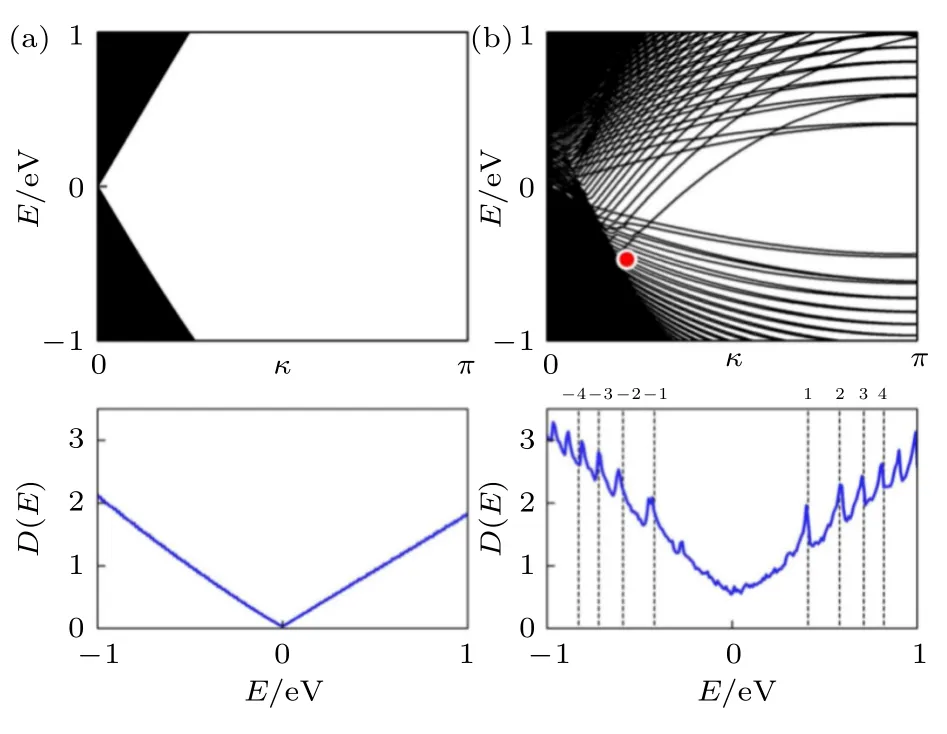
图11 176 nm 宽armchair 型石墨烯条带在未应变(a)与0.66(°)/nm 扭曲率(b)下的能带结构(上图)和态密度(下图)[126]Fig.11.Band structures (upper) and density of states(lower) of a 176 nm wide armchair graphene nanoribbon at(a) no strain and (b) twist rate=0.66(°)/nm[126].

另一个例子是关于弯曲应变调控石墨烯/六方氮化硼(G/hBN)横向异质结半金属特性的.在低维体系中实现显著并且稳定的半金属性是纳米自旋电子学研究[129−132]的重要内容.由作为半金属的石墨烯和作为绝缘体的六方氮化硼杂化而成的横向异质结中,由于石墨烯与氮化硼界面处碳原子与氮原子、硼原子之间存在电荷转移,导致界面态自旋分裂从而能够产生半金属相[133−135],而G/hBN这一低维结构的合成已在实验中实现[136−142],因此G/hBN 已然成为研究半金属性调控的优秀材料.G/hBN 在常态下半金属带隙非常小,使其半金属特性并不显著[143,144],所以如何在保持半金属性的情况下增大其半金属带隙成为了研究的一大关键.运用广义布洛赫方法,计算面内弯曲下G/hBN 横向异质结的电子能带结构.G/hBN 横向异质结以及弯曲的结构如图12 所示,计算结果如图13 所示[118].在弯曲形变下,导带中,自旋向上态向上移动而自旋向下态向下移动;价带中,自旋向上态向下移动而自旋向下态向上移动,趋势随着弯曲角度的增大而越来越明显.最终,在G/hBN 中得到了具有较大半金属带隙的稳定的半金属特性.这一计算结果证明非均匀应变可以在低维体系中实现半金属性的调控,为改善纳米自旋电子器件的性能与工艺提供了新的途径.

图12 (a)石墨烯/六方氮化硼横向异质结及其(b)面内弯曲下的结构[118]Fig.12.(a) Grapheme/hexagonal boron nitride lateral heterojunction and (b) its structure under in-plane bending[118].

图13 石墨烯/六方氮化硼横向异质结在(a)弯曲0°、(b)弯曲0.3°、(c)弯曲0.6°情况下的电子能带结构[118]Fig.13.Electronic band structures of the grapheme/hexagonal boron nitride lateral heterojunction with the bending angle of (a) 0°,(b) 0.3° and (c) 0.6°[118].

5 结论

非均匀应变对材料性质的影响一般与均匀应变的影响不同.本文介绍了二维材料中由非均匀应变诱导的赝磁场效应和挠曲电效应,并综述相关的研究进展.当然,非均匀应变对材料物性的影响不限于这两个效应.从原理上看,一个非均匀的结构变形破坏了晶体的平移以及其他对称性.这为分析材料中电子-结构关系提供了一个出发点.首先,对称性的破坏能够消除能级简并(或者引起能级的劈裂).如石墨烯条带中,弯曲变形使得自旋极化但能量简并的边缘态发生劈裂,即自旋劈裂,并最终导致半金属特性的出现.其次,对称性的破坏还会引起材料不同部分电子与声子性质的异质性.如在弯曲的氧化锌半导体纳米线中,由于价带和导带对拉伸和压缩的不同响应,造成了第二类能带偏置[145].

从材料结构特点以及现有研究进展看,弯曲变形是低维材料中产生非均匀应变场的普遍形式.如,除赝磁场效应和挠曲电效应外,实验上人们还常常通过弯曲变形来观察材料中电子色散和声子色散的红移现象.然而,从模拟计算的角度看,由于平移对称的破坏,一个简单的弯曲变形却带来了原子级计算的困难.广义布洛赫方法是解决这个问题的一个合适方法,为低维材料非均匀应变下的物性调控提供了量子力学模拟的解决方案.