偏载工况下深沟球轴承力学性能和疲劳寿命分析
2022-07-19张文昊王立萍刘嘉雯厉秀英翟敬宇
张文昊,王立萍,刘嘉雯,厉秀英,翟敬宇
(1.辽宁科技大学 机械工程与自动化学院,辽宁 鞍山 114051;2.大连理工大学 机械工程学院,辽宁 大连 116024)
深沟球轴承是机械装备的基础部件,制造和安装误差、载荷和运行条件变化等会使轴承偏载,引起接触状态和力学性能发生变化,进而产生不正常磨损甚至疲劳破坏,故有必要分析偏载工况下深沟球轴承的力学性能和疲劳寿命[1-4]。
国内外对滚动轴承力学性能和疲劳寿命做了大量研究。在力学性能分析方面,主要采用的分析方法包括静力学、拟静力学、动力学分析的解析理论,以及有限元法、网格法等数值计算仿真方法[5-9]:文献[10]基于数值分析方法计算了轴承的内部载荷分布,并基于ABAQUS软件和赫兹理论建立了单滚子接触内、外滚道模型,得到了轴承接触应力状态;文献[11]提出了一种非赫兹法求解倾斜工况下轴承的力学性能,并与赫兹法对比,结果表明非赫兹法更适用于倾斜工况下的轴承应力计算;文献[12]考虑游隙建立轴承时变刚度模型,提出采用平均刚度和刚度幅值变化率来表征刚度的时变特性,并分析了径向游隙、载荷、滚动体数对轴承时变刚度的影响;文献[13]基于ANSYS建立了圆柱滚子轴承热-应力耦合有限元模型,分析了对数修形滚子的凸度值对轴承接触应力的影响以及径向载荷和转速对最优凸度值的影响;文献[14]考虑滚子直径误差和内、外圈安装过盈量建立了滚子与滚道的接触应力和内圈中心运动轨迹计算模型,实现了对单个滚子受力的数值计算;文献[15]以轴承拟静力学和沟道控制理论为基础,考虑轴承安装过盈量等因素,计算了角接触球轴承球与内、外圈的接触刚度和轴承整体的径向刚度、轴向刚度和角刚度;文献[16]基于UGNX软件建立轴承配合模型,分析了过盈量对轴承接触应力和变形的影响;文献[17]推导了轴承内圈与轴配合尺寸和两者相互作用力的关系。
在疲劳寿命分析方面,主要是L-P寿命理论及在其基础上的改进:文献[18]在L-P寿命理论的基础上,考虑滚子寿命和滚子长度方向上的载荷分布对轴承整体寿命的影响,建立了滚子轴承基本额定寿命计算方法,并考虑过盈配合、温度等对套圈内部周向应力的影响,建立了基于次表层最大剪应力的轴承寿命修正计算方法;文献[19]基于ANSYS软件建立了薄壁深沟球轴承三维有限元模型,考虑外圈受载后弯曲变形对球载荷分布的影响,分析载荷、轴孔配合间隙及球数对球载荷及轴承寿命的影响;文献[20]考虑内、外圈运动状态对轴承应力循环次数的影响,修正了L-P寿命模型,计算了轴承内圈、外圈、滚动体以及轴承整体的寿命。
上述研究基于理论模型和仿真模型分析了在不同过盈配合量、径向游隙、温度、偏载下滚子轴承和角接触球轴承的刚度和寿命,然而关于径向载荷、偏载和过盈量对深沟球轴承力学性能和疲劳寿命影响的研究较少。鉴于此,基于接触力学理论,借助ANSYS建立有限元模型,分析径向载荷、偏载角和过盈量对轴承力学性能和疲劳寿命的影响。
1 偏载工况下深沟球轴承力学分析
在偏载工况下深沟球轴承会受到轴向载荷、径向载荷和偏载力矩,内、外圈会相对移动,如图1所示。

图1 联合载荷下内、外圈受力示意图
根据弹性壁厚圆环理论可以得到过盈配合时深沟球轴承的径向游隙变化量和初始接触角[21],内圈膨胀量为
(1)
游隙变化量为
ΔGr=-Δs,
(2)
初始接触角为

(3)
式中:I为过盈配合量;d,d1分别为内圈内、 外径;ν1,ν2分别为内圈和轴材料泊松比;E1,E2分别为内圈和轴材料弹性模量;Dzi为空心轴直径;Gr为轴承初始径向游隙;A为内、外圈沟曲率中心距。
建立内圈的力和力矩平衡方程组,即
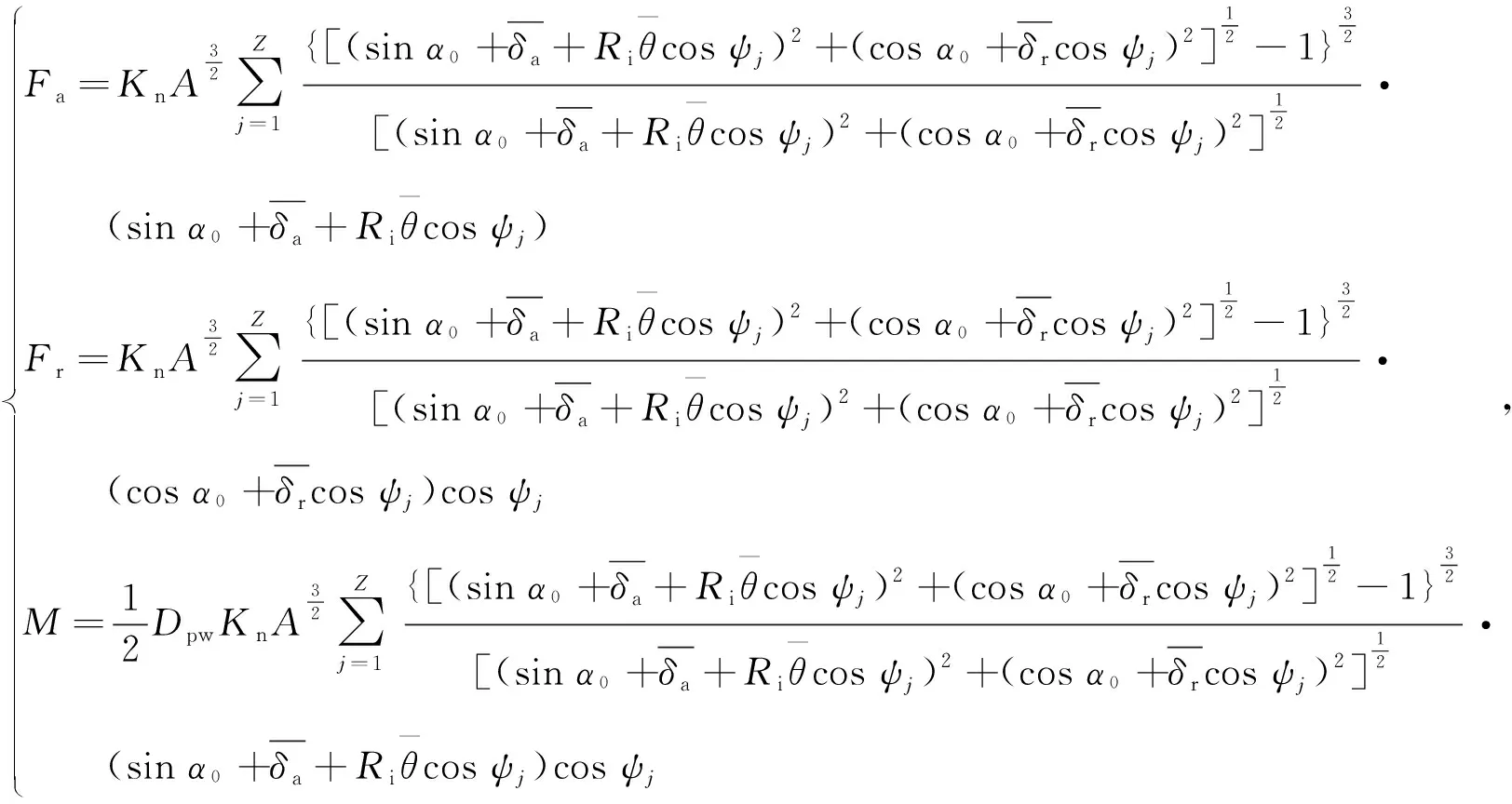
(4)

式中:Fa为轴向载荷;Fr为径向载荷;M为力矩载荷;Kn为载荷-变形系数;Z为球数;ψj为第j个球方位角;Ri为内沟曲率中心运动轨迹半径;Dpw为球组节圆直径;δa为内圈轴向位移;δr为内圈径向位移;θ为内圈角位移(偏载角)。
求解(4)式可得轴承轴向位移δa,径向位移δr和偏载角θ,进而可求得球接触载荷Qj和轴承径向刚度Kr,即
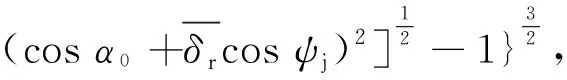
(5)
(6)
根据球接触载荷,基于L-P疲劳寿命可得球轴承疲劳寿命[22],套圈沟道额定动载荷为
(7)
套圈沟道当量接触载荷为
(8)
套圈沟道疲劳寿命为
(9)
轴承整体疲劳寿命为
(10)
式中:f为沟曲率半径系数;γ为量纲一的几何参数;Dw为球径;对于内圈,±取+,∓取-;对于外圈,±取-,∓取+;下标i,e分别代表内、外圈。
2 偏载工况下深沟球轴承有限元模型
以6012深沟球轴承为研究对象,其主要结构参数见表1。内圈材料弹性模量为210 GPa,泊松比为0.3。空心轴内外径分别为30,60 mm,材料弹性模量为210 GPa,泊松比为0.3。

表1 6012深沟球轴承主要结构参数
深沟球轴承倒角和边棱对轴承接触应力和变形影响较小,建模时忽略。拟静力学分析时不考虑保持架的影响[23],采用约束球自由度来模拟保持架的作用。建立轴承CAD模型,并导入ANSYS Workbench中。球选择四面体网格划分,内、外圈和轴选择六面体网格划分,使用“Face Meshing”工具使内、外圈和轴表面网格均匀。球、内圈及外圈的网格密度为1 mm,轴网格密度为2 mm。该模型共生成105 225个单元和370 509个节点,有限元模型网格划分模型如图2所示。

图2 6012轴承网格划分模型
每个球与内、外圈沟道均需设置接触对,共计26个接触对。轴与内圈内表面也需设置接触对,为摩擦接触。设内、外圈沟道表面为目标面,球表面为接触面,摩擦因数为0.15。通过修改轴与内圈接触设置中的“Offset”值调整过盈量,过盈量为0~0.02 mm。
施加约束和载荷条件(图3):1)外圈外表面施加固定约束;2)轴内表面施加旋转副,仅保留y方向的平移自由度和z方向的旋转自由度;3)保留内圈在y方向的平移自由度;4)建立柱坐标系,在该坐标系下限制球公转方向的转动自由度。在轴内表面施加径向载荷,并在其旋转副上施加角位移载荷。
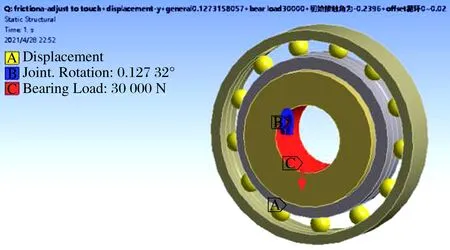
图3 约束与载荷设置
基于有限元模型计算结果以及后处理工具可得球接触载荷和轴承径向位移,再通过(6)~(10)式可得轴承径向刚度和疲劳寿命。
3 模型验证
由于力学模型和有限元模型轴承径向刚度和疲劳寿命均通过将球接触载荷和轴承径向位移的计算值代入(6)~(10)式得到,在此取球接触载荷和轴承径向位移验证有限元模型。
轴向载荷为0,过盈量为0 时,在6种工况(表2)下轴承的径向位移和工况3下球接触载荷分布(在径向载荷作用方向球方位角为0°,方位角±90°范围为主要承载球,主要分析该范围内的球接触载荷)分别如图4和图5所示,最大误差为2%,在允许范围之内,说明了有限元模型的正确性。

表2 工况条件

图4 在6种工况下6012轴承的径向位移
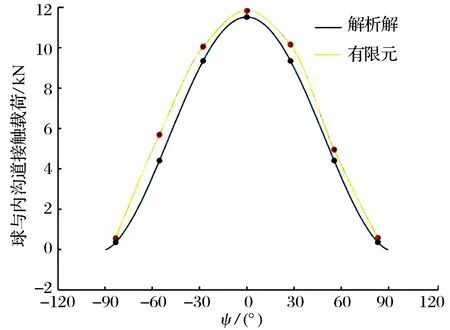
图5 在工况3下球接触载荷分布
4 轴承力学性能和疲劳寿命分析
基于有限元模型分析径向载荷、偏载角、过盈量对深沟球轴承力学性能和疲劳寿命的影响。
4.1 径向载荷
在轴向载荷为0,偏载角为0.127°,过盈量为0.02 mm时,径向载荷对轴承力学性能和疲劳寿命的影响如图6所示:1)球接触载荷和接触应力随径向载荷增大而增大;2)轴承径向刚度随径向载荷增大而增大,但增大幅度随径向力增大而减小,这是由于随径向载荷增大,轴承内部游隙和球间距变大, 接触区球的接触面积减小, 球与沟道的接触刚度增幅减小, 径向刚度增大幅度随径向力增大而减小;4)轴承疲劳寿命随径向载荷增大而减小。

(a)球接触载荷
4.2 偏载角
在轴向载荷为0,径向载荷为30 kN,过盈量为0.02 mm时,偏载角对轴承力学性能和疲劳寿命的影响如图7所示:1)随偏载角增大, 球接触载荷变化较小,方位角0°及其附近的球接触载荷增大,其他位置的球接触载荷减小; 2)随偏载角增大,方位角为0°的球接触应力增大, 0°附近的球接触应力先减小再增大, 其他位置的球接触应力减小;3)轴承径向刚度随偏载角增大而减小,这是由于随偏载角增大,球与内、外圈沟道的接触角增大,从而部分抵抗径向位移的能力转化为抵抗轴向位移的能力,轴承径向刚度减小;4)随偏载角增大,轴承疲劳寿命先增大后减小,在偏载角为0.137°时轴承疲劳寿命最大,说明存在合适的偏载角使轴承寿命最佳。
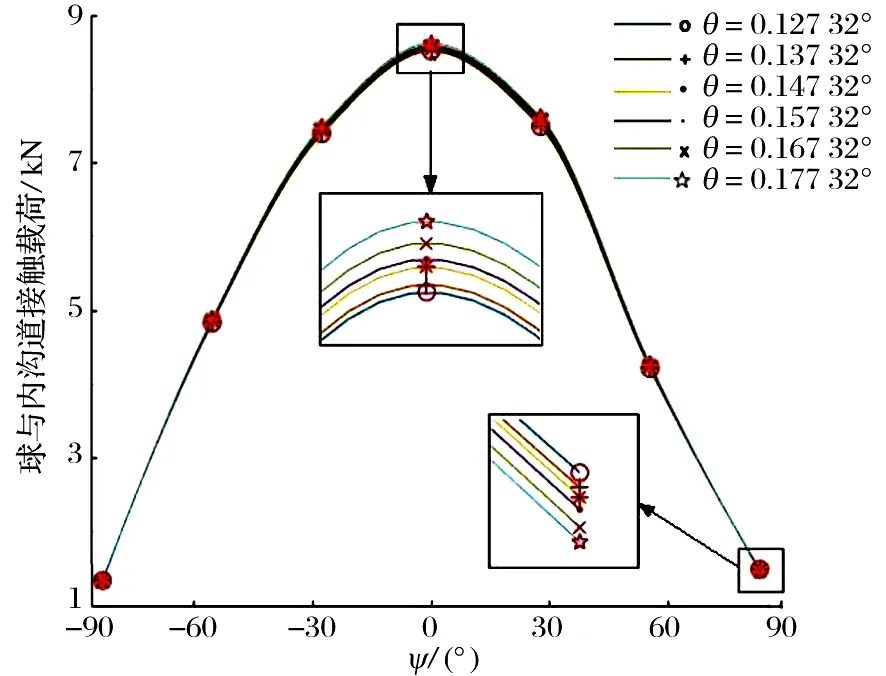
(a)球接触载荷
4.3 过盈量
在轴向载荷为0,径向载荷为30 kN,偏载角为0.127°时,过盈量对轴承力学性能和疲劳寿命的影响如图8所示:1)随过盈量增大,方位角为0°附近的3个球接触载荷和接触应力减小,其余位置的球接触载荷和接触应力增大,这是由于随过盈量增大,轴承内圈膨胀量增大,两侧接触区球的接触面积逐渐增大,承担了更多的载荷;2)随过盈量增大,轴承径向刚度先减小后增大,这是因为当过盈量增大时,轴承内圈在所受膨胀力、径向力和偏载角的联合作用下, 轴承径向位移也随之增大,轴承径向刚度减小,但当过盈量增大到一定值时,轴承内部间隙减小,球与内、外圈沟道的接触刚度增大,轴承径向刚度增大;3)随过盈量增大,轴承疲劳寿命增大,这是由于随过盈量增大,两侧接触区球的接触面积逐渐增大,两侧的球承担了更多的载荷,球受力均匀,轴承疲劳寿命增大。
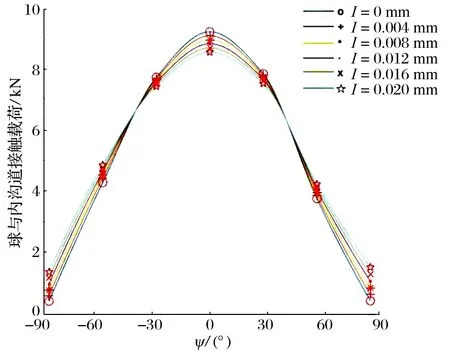
(a)球接触载荷
5 结论
考虑偏载和过盈量建立深沟球轴承力学分析模型和有限元模型,以6012深沟球轴承为研究对象,验证了有限元模型的正确性,并分析了径向载荷、偏载角和过盈量对球与内圈的接触载荷和接触应力、轴承径向刚度和疲劳寿命的影响,得出如下结论:
1)轴承疲劳寿命并不一直随偏载角增大而减小,存在合适的偏载角使轴承疲劳寿命最佳;
2)在一定的过盈量范围内,随过盈量增大,球受力均匀,轴承疲劳寿命增大。
本研究的数学模型中涉及了轴向载荷,但文中并未分析轴向载荷对轴承力学性能和疲劳寿命的影响,后续有待进一步研究。
