带有logistic源的三维趋化系统弱解的最终光滑性

姜 永 峰

(电子科技大学 数学科学学院， 成都 611731)

0 引 言

生物学、物理学和医学等自然科学中存在着大量的非线性现象，这些非线性现象在数学上可利用非线性偏微分方程组来进行模拟和刻画，特别地，对于生物趋化方程组的研究是当前数学领域中一个具有意义与价值的研究方向。其中，趋化性是指细胞朝着有利于自身生长的环境移动的一个特征。一般地，如果细胞朝着化学信号浓度高的方向移动称为化学吸引，反之称为化学排斥。对于趋化现象，最早是由Keller和Segel[1]在20世纪70年代提出的一个开创性的描述趋化性的数学模型：

(1)

‖u0‖Lq(Ω)<ε、‖v0‖Lp(Ω)<ε

一般地，由于经典的Keller-Segel系统式(1)只考虑了细胞的趋化性和扩散。但是，在实际的生物学背景下，大多数情况下都是需要考虑细胞的产生和死亡，在数学模型上体现出来就是 logistic 增长项的出现，因此便得到如下系统：

这里，κ∈和μ>0分别表示出生率和死亡率和参数α>1。在2015年，Xiang[6]证明了当空间维数d≤2，参数α=2时，对于任意小的μ>0。 上述系统存在全局一致有界解。

特别地，对于结构简单的细胞也会朝着消耗营养物质的方向运动，故与上述系统相对应的一个典型变体是考虑如下具有信号消耗机制的趋化模型

(2)

基于以上所得到的结果，研究了当1<α<2时，对于任意充分光滑的初始值，如下一类具有 logistic 增长项的趋化方程组在三维情形时弱解的最终光滑性：

(3)

其中，Ω⊂R3是一个具有光滑边界∂Ω的有界区域，给定的非负初值满足：

(4)

这里首先给出本文的主要结果。

定理1 设Ω⊂R3是一个具有光滑边界的有界区域，那么对于满足式(4)的任意初始值(u0,v0)，系统式(3)的解(u,v)满足对所有的T>0和γ∈(0,1)，有

1 准备工作

为了获得式(3)的弱解的最终光滑性，基于文献[14]，对任意的ε∈(0,1)，这里首先考虑如下正则化系统：

(5)

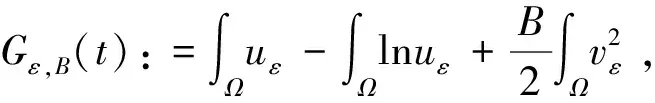
(6)

(7)

一方面，由式(7)可以直接得到

(8)

与

(9)

将式(8)、式(9)代入式(7)，有

故而引理1成立。

引理2 设对任意的ε>0，存在常数k>0与C>0,使得

(10)

(11)

证明对任意的ε>0和t>0，将式(6)在0-t上积分，可得

特别地，对任意的t>0，有

(12)

另外，由式(12)可以得到

即引理2成立。

引理3 设对任意的η>0，存在T>0，使得对所有的t>T时，满足

证明对式(5)的第二个方程在Ω×(0,t)上积分，可得

由文献[14]中的引理4.1，可知

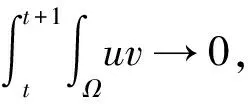
(13)

一方面，由Poincaré不等式、Hölder可得

(14)

另外，由Gagliardo-Nirenberg不等式、文献[14]的引理2.4和引理4.1可知，存在正常数C2，C3，C4，满足

(15)

故引理3证毕。

接下来，通过应用Sobolev最大正则性的方法，可得uε与vε更高阶的正则性估计。

引理4 设p∈(1,∞)，则存在常数C>0，ε0>0，T>0，γ∈(0,1)，使得对任意的t>T，ε∈(0,ε0)，满足

进一步，有

证明该引理的证明可以参考文献[15]中引理3.13的证明。

引理5 设p∈(1,∞)，则存在常数C>0，ε0>0，T>0，γ∈(0,1)，使得对任意的t>T，ε∈(0,ε0)，满足

进一步，有

证明类似地，该引理的证明可以参考文献[15]中引理3.14的证明。

引理6 设存在常数γ∈(0,1)，T0>0和序列(εj)j∈N⊂(0,1)，使得对任意的t>T0，当ε=εj→0时，有

此外，存在正常数C，使得

证明由引理4和引理5直接可证得引理6.

引理7 设存在常数γ∈(0,1)，T>0，使得

证明设ξ:R→[0,1]是一个光滑单调的函数，并且在(-∞,0]上满足ξ≡0，在(1,∞)上满足ξ≡1.对任意的t0∈R，记ξt0:=ξ(·,-t0). 则ξv是以下方程的解

最后，结合ξ的定义，可以得到

同样地，ξu是以下初边值问题的解：

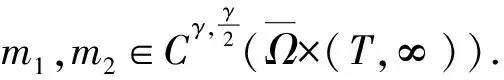
于是，引理7证毕。

定理1的证明：由引理7可以直接证得定理1。

2 结论与讨论

生物趋化方程组的研究具有重要的理论价值和极强的现实意义。本文利用能量方法、先验估计等一系列偏微分方程的理论知识研究了一类具有logistic源的信号消耗型趋化方程组。证明了结论: 当空间维数d=3时，参数α满足1<α<2时，带有logistic源的三维趋化系统的弱解在一定的等待时间后变成经典解。关于此类模型解的适定性的研究，目前已有的结果都是建立在α≥2或者对初值有小性假设的前提下。而对于logistic 源为次二次增长形式时的结论还比较少，仍然有许多问题还值得进一步地研究。比如:于维数d>3的情况，该系统的弱解是否是最终光滑的。同样地，对带有多孔介质趋化系统的解的最终光滑性也是值得进行相应研究。

对非线性抛物型方程解的适定性进行研究，目前是数学领域中一个重要的研究方向。一方面，这些非线性的抛物型方程有着重要的理论价值和极强的现实意义。另一方面，也提出了许多具有挑战性的数学问题，对于这些问题的研究将会有助于完善数学的理论方法。