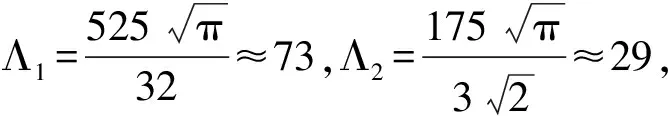一类非线性项带导数的分数阶微分方程边值问题正解的存在性和多解性
2022-07-18褚丽敏胡卫敏苏有慧
褚丽敏,胡卫敏,苏有慧
(1.徐州工程学院 数学与统计学院,江苏 徐州 221018;2.伊犁师范大学 a.数学与统计学院;b.应用数学研究所,新疆 伊犁 835000)
自然生活中的很多问题用通常的整数阶微分方程很难解释与描述,而与整数阶微分方程相比,分数阶微分方程在描述自然、物理、化学等现象时更有普遍性和准确性.因而,近些年分数阶微分方程吸引了越来越多学者的关注,并取得了一些重要的成果[1-9].
文献[10]研究了一类Riemann-Liouville型分数阶微分方程边值问题
正解的存在性,其中Dα表示α阶Riemann-Liouville分数阶导数,2<α≤3,1<β≤2,1+β≤α,f∈C([0,1]×[0,+∞),(0,+∞)).
文献[11]研究了一类Riemann-Liouville型分数阶微分方程多点边值问题

文献[10]考虑了Riemann-Liouville型分数阶微分方程边值问题正解的存在性,但其非线性项不包含导数,而研究非线性项带导数的分数阶微分方程,更具有普遍意义和现实意义.文献[11]研究了非线性项内含导数的分数阶问题3个正解的存在性.
受以上文献启迪,本文研究非线性项内含导数的Riemann-Liouville型分数阶微分方程
问题(1)
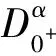
1 预备知识
定义1[12]设α>0,使得函数u:(0,+∞)→R的Riemann-Liouville分数阶积分定义成
定义2[12]设α>0,使得函数u:(0,+∞)→R的Riemann-Liouville分数阶导数是
其中:n-1≤α u(t)=c1tα-1+c2tα-2+…+cntα-n, 其中:ci∈R,i=1,2,…,n,n=[α]+1. 引理2[12]若α>0,β>0,u∈L(0,1),则有 1)‖Ax‖≤‖x‖,∀x∈P∩∂Ω1且‖Ax‖≥‖x‖,∀x∈P∩∂Ω2; 2)‖Ax‖≥‖x‖,∀x∈P∩∂Ω1且‖Ax‖≤‖x‖,∀x∈P∩∂Ω2; 运用Leggett-Williams不动点定理证明问题(1)的多解性.设Ω是巴拿赫空间X中的锥,Ω上的一个非负连续凹泛函α,为α:Ω→[0,+∞),并且满足: α(tx+1-ty)≥tα(x)+(1-t)α(y),∀x,y∈Ω,0≤t≤1. 令 Ωr={u∈Ω|‖u‖ Ωa,b,d={u∈Ω|b≤α(u),‖u‖ 3)当u∈Ω(a,b,c)且‖Tu‖>d时,有α(Tu)>b,则A至少有3个不动点u1、u2、u3满足 ‖u1‖ 引理5若3<α≤4,函数y∈C[0,1],则分数阶微分方程边值问题 有唯一解 其中 问题(2) 证:由引理2可知 其中,3<α≤4.由边值条件u(0)=u′(0)=u″(0)=0,意味着c2=c3=c4=0, 又因为u′(1)=0,故 综上 引理6引理5中的格林函数满足以下性质: 1)对与任意的t,s∈[0,1],G(t,s)∈C([0,1]×[0,1]); 2)对与任意的t,s∈[0,1],G(t,s)≥0,G′(t,s)≥0; 证:性质1)易得.下面主要证明性质2)、3)、4).为了方便表达,令G1(t,s),G2(t,s)为 由于t,s∈[0,1],显然0 当0≤s≤t≤1时, 当0≤t≤s≤1时, 综上可得,对与任意的t,s∈[0,1],有G(t,s)≥0,同理G′(t,s)≥0,故性质2)成立. 因为 当0≤s≤t≤1时, 当0≤s≤t≤1时, 根据性质3)有 问题(3) 令 根据洛必达法则, 因此 故性质4)成立. 本节在Banch空间上构建了一个全连续泛函,将边值问题解的存在性转化为研究这个全连续算子的不动点存在问题.定义Banch空间 E={u(t)|u(t)∈C[0,1]}, 定义锥P⊂E为 定义算子T 引理7设u∈U, 则 证:对∀u∈U,t∈[0,1],有u(t)-u(0)=u′(ξ)t.由于u(0)=0,故 因此 引理8设f∈C([0,1]×[0,+∞)×(-∞,+∞),[-∞,+∞)),则算子T:P→P是全连续的. 证:对∀u∈P,因为f和G(t,s)具有非负性,所以(Tu)(t)≥0.又由引理6中4)得 因此T(P)⊂P,即T:P→P. 证T:P→P是一致有界的.令 Ω={u(t)∈E:‖u(t)‖≤R,R>0,t∈[0,1]}. 有 KL1, KL2, 因此 ‖Tu‖=max{‖Tu‖1,‖Tu‖2}≤max{KL1,KL2}, 故T(Ω)是一致有界的. 证明算子T:P→P是等度连续的.因为G(t,s)和G′(t,s)在[0,1]×[0,1]上是连续的,所以G(t,s)和G′(t,s)在[0,1]×[0,1]上一致连续.取t1,t2∈[0,1],对任意ε1,ε2>0,存在常数δ>0,当|t2-t1|<δ时,有 且 进一步有 |(Tu)(t2)-(Tu)(t1)|≤ 且 |(Tu)′(t2)-(Tu)′(t1)|≤ 取ε=max{ε1,ε2},则 ‖(Tu)(t2)-(Tu)(t1)‖=max{|(Tu)(t2)-(Tu)(t1)|,|(Tu)′(t2)-(Tu)′(t1)|}<ε, 故算子T:P→P是等度连续的. 综上,由Ascoli-Arzela定理可知T(Ω)是紧集,所以T:P→P全连续. 为了方便证明,记 定理1设f∈C([0,1]×[0,+∞)×(-∞,+∞),(-∞,+∞)),若存在两个常数m>n>0,且满足如下条件: 1)f(t,u(t),u′(t))≤mΛ1,(t,u(t),u′(t))∈[0,1]×[0,m]×[0,m]; 2)f(t,u(t),u′(t))≥nΛ2,(t,u(t),u′(t))∈[0,1]×[0,n]×[0,n]. 则边值问题(1)至少存在一个正解. 证:首先令 Ωm={u∈E:‖u‖ 则对∀u∈∂Ωm,都有0 因此∀u∈P∩∂Ωm,有 ‖Tu‖≤‖u‖. 令 Ωn={u∈E:‖u‖ 则对∀u∈∂Ωn,都有0 因此∀u∈P∩∂Ωn,有 ‖Tu‖≥‖u‖. 由引理3可知算子T存在一个不动点u,即u是边值问题(1)的一个正解. 利用Leggett-Williams不动点定理给出分数阶微分方程边值问题(1)3个解的存在性定理. 定理2设f∈C([0,1]×[0,+∞)×(-∞,+∞),(-∞,+∞)),若存在两个正数0 1)f(t,u(t),u′(t)) 3)f(t,u(t),u′(t))≤cΛ1,(t,u(t),u′(t))∈[0,1]×[0,c]×[0,c]. 则边值问题(1)至少存在3个解u1,u2,u3,满足 证:令 故有{u∈Ω(θ,b,d)|θ(u)>b}≠∅. 另一方面,若u∈Ω(θ,b,d),有 b≤θ(u)≤u(t)≤‖u‖≤d. 根据条件2)可得 即u∈Ω(θ,b,d),θ(Tu)>b,满足引理4中条件1). 对∀u∈Ω(θ,b,d),和‖Tu‖>b,类似可得θ(Tu)>b,这意味着引理4中条件3)成立. 综上,由引理4则边值问题(1)至少有3个正解u1,u2,u3,满足 例子1考虑非线性分数阶微分方程边值问题 例子2考虑非线性分数阶微分方程边值问题


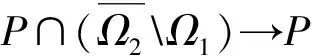

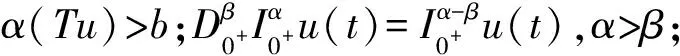

2 Green函数及其性质
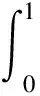
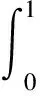

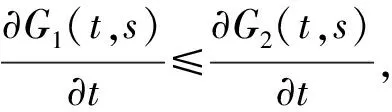
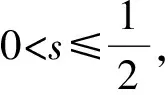

3 全连续算子

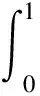
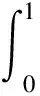

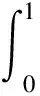
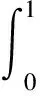
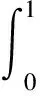
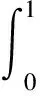
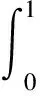
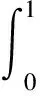
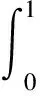
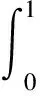
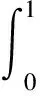
4 一个解的存在性
5 3个解的存在性
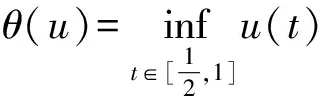



6 应用举例