风浪流作用下考虑筒-土接触的吸力筒导管架响应

潘宏冠， 陈超核,2*， 倪道俊， 樊天慧,2

(1. 华南理工大学 土木与交通学院， 广东 广州 510641；2. 南方海洋科学与工程广东省实验室(珠海)， 广东 珠海 519080；3. 三峡珠江发电有限公司， 广东 广州 510030)

0 引 言

海上风电基础具有重心高、所受海洋环境载荷复杂、承受水平力和倾覆弯矩大等特点。降低基础造价、提高施工工效是海上风电走向平价上网的必由之路。目前国内外研究和应用的海上风电基础从结构形式上主要有桩基础、筒型基础和漂浮式基础。与桩基础相比，筒型基础中的吸力筒导管架基础具有可整体安装、施工工效高、便于拆卸、可循环使用、便于运输等优点[1]。使用吸力筒导管架基础可大幅度提高岩基海床风电场的建设效率、缩短建设周期、降低风场造价。

吸力筒导管架作为一种新型的海上风电基础形式，其承载机理和失效模式与传统的桩基础有着显著的不同。近年来，国内外学者对吸力筒基础进行大量研究。朱焰[2]、杨俊等[3]对筒型基础的承载机理和失效模式进行理论研究，建立吸力筒参数的基本设计方法。TRAN等[4]、ISHFAQ等[5]等通过一系列有限元分析，研究三筒吸力筒的筒高、直径、筒间距之间的比例关系对承载力的影响，并提出优化设计方案。WANG等[6]通过有限元分析研究复合筒基础的承载性能，结果表明增加隔板能提升筒型基础在非匀质黏土中的弯矩承载力。马鹏程等[7]通过大比尺模型试验研究复合筒基础在受荷过程中受到土压力的变化规律，结果表明在结构受荷过程中不能将筒内土体和筒体看成一个整体进行分析。在以往的研究中，对单柱复合筒的研究较多，对吸力筒导管架的研究较少；对吸力筒安装过程中的渗流[8]、挤土效应[9]、受力特性[10]等研究较多，对安装后结构在极端工况下的响应研究较少；以往的研究大多把环境载荷简化为集中载荷、均布载荷或正余弦载荷，把基础边界条件简化为固定约束或弹簧约束，对基础进行风浪流-筒体结构-土体的耦合分析研究较少。

本文以中国南海某实际海上风电吸力筒导管架基础为分析对象，以50 a重现期的极端工况作为载荷条件，建立吸力筒导管架与土体耦合的三维有限元模型，分析风浪流联合作用下基础的结构动力响应。分析结果能对基础沉降量的合理预留、基础最佳安装方向、基础承载力校核等实际工程问题提供科学参考。

1 计算分析理论

1.1 波浪载荷

当吸力筒导管架结构特征尺寸与波长的比值D/L≤0.2时，工程上广泛采用Morison方程计算其波浪载荷：

(1)

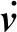
令CM=1+Ca，则式(1)可写为

(2)

将式(2)左边写成运动方程：

(3)

式中：M、C、K分别为结构质量矩阵、阻尼矩阵和刚度矩阵；u为结构位移列阵。合并同类项，有：

(4)

式中：Ma为附加质量矩阵；右边为单位长度的水动力矢量，第1项为与流体加速度成正比的惯性力项，第2项为与流体速度平方成正比的拖曳力项[11]。将式(4)右边从海底至波面位移积分，即可求得作用在结构物上的波浪力。

ANSYS APDL提供多种波浪理论模型，如深度衰减经验修正的微幅波理论模型、Airy波理论模型、流函数波浪理论模型和Stokes五阶波理论模型等。由于Stokes五阶波理论模型更接近实际波浪，本研究选用Stokes五阶波理论模型进行计算。

1.2 流载荷

海流载荷是海洋结构物的主要载荷之一，对海上风电基础的稳定性有着显著影响。海流通常近似处理为一种稳定的平面流。海流与单位长度圆柱形结构物间的相互作用可表示为

(5)

式中：fc为单位长度圆柱上的海流载荷；vc为海流速度。

将式(5)右边从海底至波面位移积分，即可求得作用在结构物上的海流力。

波浪在波峰与波谷之间会交替拉伸或压缩海流剖面速度，因此有必要对海流剖面速度进行修正[12]。ANSYS APDL提供几种不同的波流耦合作用下海流剖面速度的修正方法，如图 1所示。当波流耦合作用方式序号KCR取0时，海平面以下使用输入的海流剖面速度，海平面以上使用最高的海流剖面速度；当KCR取1时，海流剖面速度被线性拉伸或压缩以适应波浪速度；当KCR取2时，海流剖面速度被拉伸或压缩，且所有的海流方向必须一致以满足连续性方程；当KCR取3时，海流剖面速度被非线性拉伸或压缩。由于本工况下波幅较大，为满足API RP 2A-WSD设计规范，取KCR=2，采用满足连续性方程的波流耦合作用方式对海流剖面速度进行修正。

图1 波流耦合作用下海流剖面速度修正

1.3 风载荷

极端风载荷对海上风电的安全稳定性影响较大。空气在一定速度下运动作用在曲面上产生风压，其空气动能函数为

(6)

式中：p为基本风压；ρa为空气密度；vT,Z为T平均时间内Z高度处对应的平均风速。

总风力为

Fw=pCZCSAw

(7)

式中：CZ为受风结构高度因数；CS为构件形状因数(圆柱体取0.5)；Aw为承受风压的结构物迎风面积。

1.4 筒-土接触

吸力筒与土接触会产生相互作用。接触分析是一种高度非线性的行为，随着接触状态的改变，接触表面的法向和切向刚度都有显著变化[13]。ANSYS提供多种接触算法，对于实体表面的法向接触问题，较常用的有罚函数法。罚函数法认为接触压力与渗透量有关，当筒土分离时接触压力为零。采用罚函数法求解接触问题，相当于在接触表面的节点上设置一系列法向界面弹簧，如图2所示。当接触面的间隙小于0，即发生渗透时，接触压力为

图2 接触渗透示例

Fn=KnXp

(8)

切向接触问题采用库伦(Coulomb)摩擦模型，认为切向接触力即界面摩擦力τ不大于临界摩擦力τcrit：

τ<τcrit=μFn

(9)

式中：μ为筒土间摩擦因数。

当界面摩擦力小于临界摩擦力时，接触面处于黏滞状态，没有发生位移；当界面摩擦力大于临界摩擦力时，接触面间发生滑移。

1.5 筒基承载力

吸力筒基础与传统桩基础的承载特性有所不同。传统桩基础的承载力主要由侧摩阻力和端承力提供，而吸力筒基础的承载力除了由侧摩阻力和端承力提供外，还由顶盖板承力提供。本工程海域的地质条件复杂，吸力筒顶盖板和大部分筒壁所处土层为淤泥质土层，筒底端所处土层为粗砂层。因此，需结合黏性土和和非黏性土的承载力计算方法进行计算。

对于上端开口的短桩，API-RP 2A WSD给出极限承载力计算方法为

Qd=Qf+Qp=fAs+qAp

(10)

式中：Qd为极限承载力；Qf为桩侧摩阻力；Qp为桩端阻力；f为单位桩侧摩阻力；As为桩侧面积；q为单位桩端阻力；Ap为桩端面积。

对于上端闭口的吸力筒，在计算竖向承载力时还须加上顶盖板阻力，即

世界剪纸看中国，中国剪纸看蔚县。蔚县位于张家口南面，是联通口内外的咽喉要道，商贾云集于此，能工巧匠往来频繁。正是多元文化的融合，各个民族的交流，在这个人杰地灵的地方，催生了民族工艺的一朵奇葩——蔚县剪纸。

(11)

式中：QT为顶盖板阻力；q′为单位顶盖板阻力；AT为顶盖板面积。

黏土中单位侧摩阻力fi和砂土中单位侧摩阻力fj分别为

fi=αc

(12)

fj=βp0

(13)

式(12)和式(13)中：c为土的不排水抗剪强度；β为轴摩擦因数，中密粗砂取0.37；p0为有效土压力；α为无量纲因数，计算式为

(14)

式中：ψ=c/p0。

黏土中单位顶盖板阻力qi和砂土中的单位筒端阻力qj分别为

qi=9c

(15)

qj=p0Nq

(16)

式中：Nq为无量纲因数，根据本工程海域土体参数，查表取Nq=20。

2 数值模型建立

2.1 模型参数

基于某海上风电项目，对吸力筒导管架基础和土体进行建模。该海域水深为27.69 m，吸力筒导管架相关参数和土体相关参数如表1和表2所示。导管架与塔筒之间通过过渡段进行连接，塔筒共有4段，参数如表3所示。由于下端塔筒需要承受更大的载荷，塔筒采用渐变式直径设计。表3中，尺寸参数第1项为该段塔筒下端直径、第2项为上端直径、第3项为该段长度。为降低土体边界对分析结果的影响并平衡计算量，土体计算区域取200 m×200 m×38 m的长方体模型。

表1 吸力筒导管架主要参数

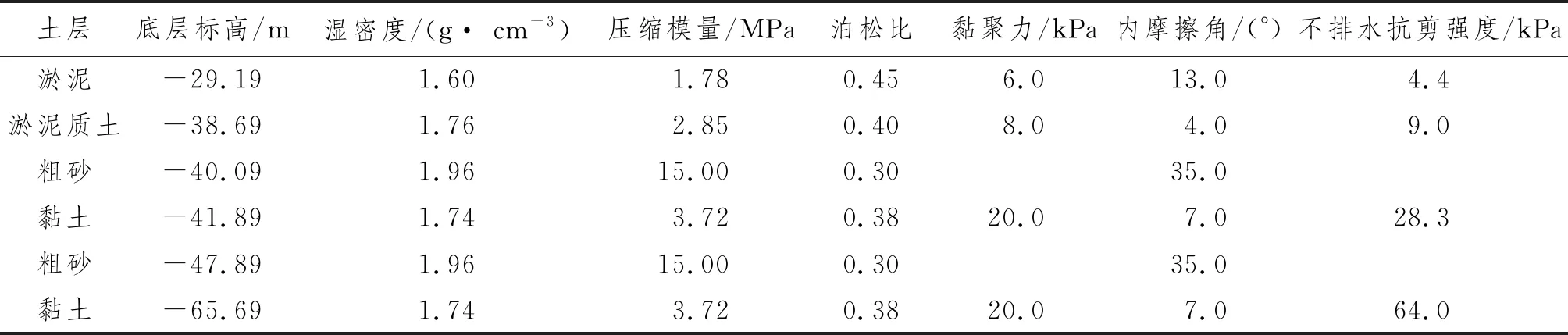
表2 各层土体参数

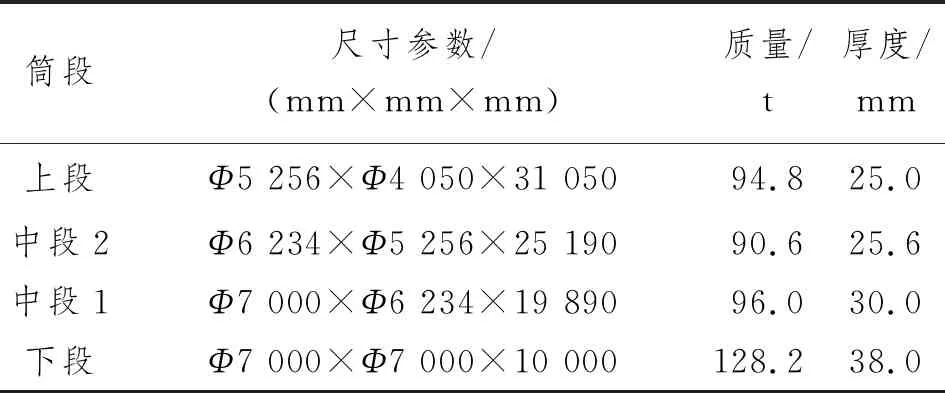
表3 塔筒参数

2.2 网格划分及边界条件

采用扫掠划分方法对结构和土体进行网格划分，在ANSYS中建立如图3所示的有限元模型。其中：土体基于Drucker-Prager本构模型，采用Solid 45实体单元；吸力筒和塔筒采用Shell 181面单元；加强筋采用Beam 189梁单元；导管架结构采用能够计算水动力的Pipe 59管单元；主机和叶片的质量以Mass 21结构质量单元的形式均布至塔筒顶端的节点上。

当一个对象比另一个对象刚度大很多时，可视为刚性体-柔性体接触问题。接触分析需要在接触面建立接触对。将刚度较大的吸力筒界面定义为目标面(TARGET)，刚度较小的土体界面定义为接触面(CONTACT)，在接触区域生成目标单元和接触单元。接触区域包括筒体内壁与筒内土体，筒体外壁与筒外土体，盖板内壁与筒内土体，接触状态如图3所示。通过定义法向刚度因子FKN，程序会根据变形体单元的材料特性估算接触刚度。经过计算，发现在本模型中FKN取0.2能获得不错的收敛性。接触面的初始容许穿透容差指定了接触面的初始穿透范围。通过迭代调整，当最大初始容许穿透容差为0.15时，可以将整个目标面(连同变形体)移动至指定的初始穿透范围，使其成为闭合接触的初始状态。结构与土体之间的摩擦阻力对基础的沉降和抗倾覆稳定性发挥重要作用。基于工程地勘资料并结合文献[14-15]，将筒与淤泥质土及软塑黏土的摩擦因数取0.20，筒与饱和粗砂的摩擦因数取0.28。在网格划分完成后，对土的4个侧面施加法向位移约束，对底面施加位移和转角全约束。

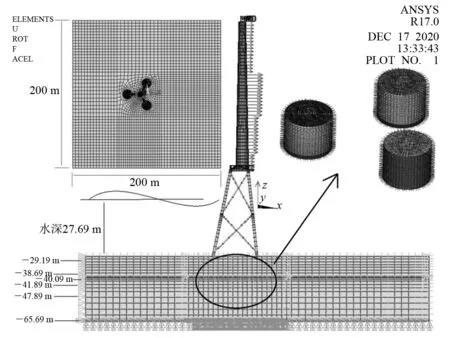
图3 吸力筒导管架有限元模型

2.3 计算工况

据水文观测站统计，五十年一遇累计概率为1%的波高为13.9 m，波周期为14.1 s，表层、0.6H层(H为水深，0.6H层即水面以下0.6倍水深处)和底层海流流速统计值分别为209.1 cm/s、140.2 cm/s、99.4 cm/s，距海平面高度10～120 m处10 min平均风速如表4所示。基于第1节介绍的风浪流理论，在ANSYS APDL中对吸力筒导管架基础进行载荷施加。

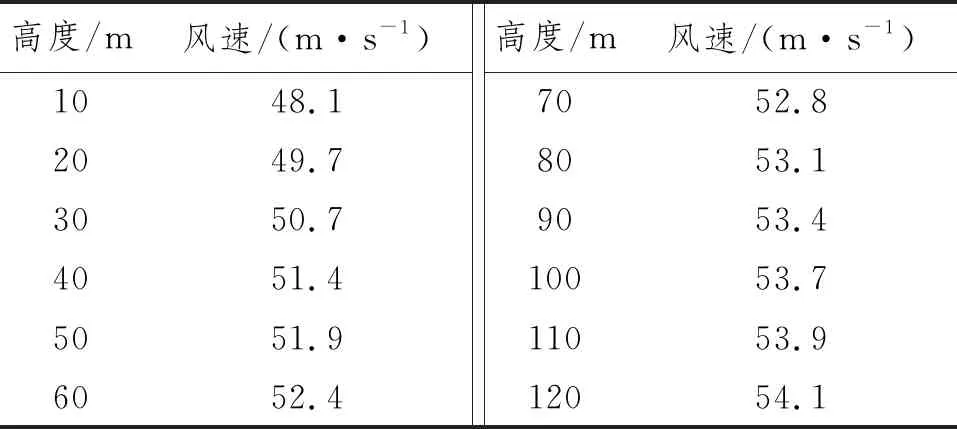
表4 距海平面10～120 m处五十年一遇10 min平均风速

3 结果分析

3.1 波浪相位与浪流方向的影响

在采用Stokes五阶波理论时，波浪相位角φ的取值对于作用在结构上的波浪载荷有较大影响。当波浪作用于结构物时，其作用力的大小与波浪相位角紧密相关。在进行结构静力分析时，假定波浪以最大作用力作用于结构上，以此来考虑结构受波浪载荷的最不利工况。因此，在进行静力分析时，有必要对波浪相位角φ进行0°～360°全方位搜索，以确定波流耦合力最大时的相位角取值。通过ANSYS APDL命令流功能，编制相应的波浪相位角搜索程序，提取不同相位角作用时吸力筒底部的波流耦合作用节点反力，并绘制如图4所示的波流耦合节点反力-相位角关系曲线。由图4可知，当相位角为34°时，波流耦合节点反力最大。后续分析的相位角取值均基于此计算结果。

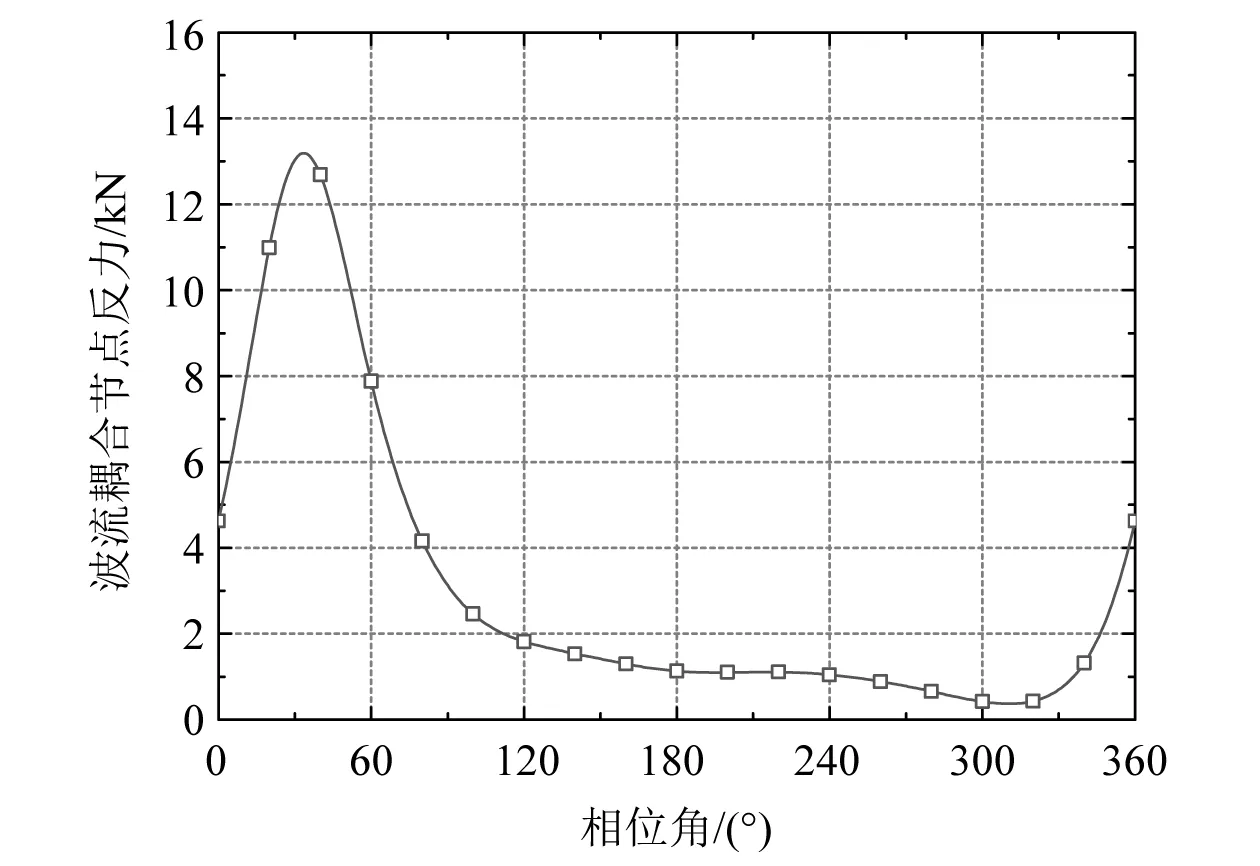
图4 波流耦合节点反力-相位角关系曲线

场址海域波浪测站的周年观测资料显示，观测期间常浪向为ESE(东南偏东)，出现概率为52.04%，浪向出现在ESE～SSE(东南偏南)的概率大于90%。讨论浪流方向对吸力筒导管架基础的影响有助于找到吸力筒的最佳安装方向。夏可等[16]的研究表明，导管架基础所受载荷会随浪流夹角的增大呈现略微增大后减小的趋势。出于简化计算，将浪流夹角为0°视为最不利工况。由于吸力筒导管架基础具有轴对称性，仅计算浪流与结构相对夹角在0°～180°的结构应力。浪流与吸力筒导管架结构的相对作用方向如图5所示。

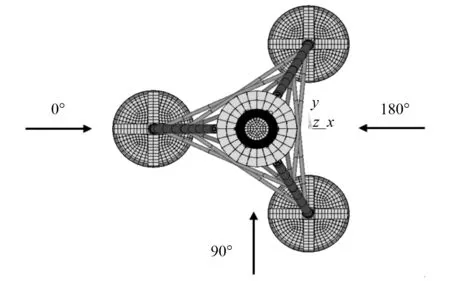
图5 浪流作用方向

改变浪流与结构相对作用方向，每隔15°提取一次结构最大应力，统计如图6所示浪流作用方向与结构的最大应力的关系。由于吸力筒导管架基础具有轴对称性，结构的最大应力关于0°和180°对称。由图6可知，当浪流作用角为120°～240°时，结构所受最大应力较小，且当作用角为120°和240°时结构最大应力最小。

图6 不同浪流作用角下结构最大应力

3.2 吸力筒导管架强度校核

五十年一遇极端风浪流载荷下的最大结构等效应力如图7所示。由图7可知，在极限工况下吸力筒导管架基础的最大等效应力为220 MPa，小于DH36高强度结构钢的屈服强度335 MPa，强度满足要求。最大应力出现在背浪侧的筒盖板上，背浪侧筒盖板的应力显著大于迎浪侧筒盖板应力。在风浪流载荷弯矩的作用下，导管架倾向于往背浪侧倾覆，导致背浪侧的2个筒受压增大，迎浪侧的筒受压减小。因此，在吸力筒设计阶段可根据吸力筒基础的安装方向对迎浪侧和背浪侧的吸力筒壁厚进行差异性调整。

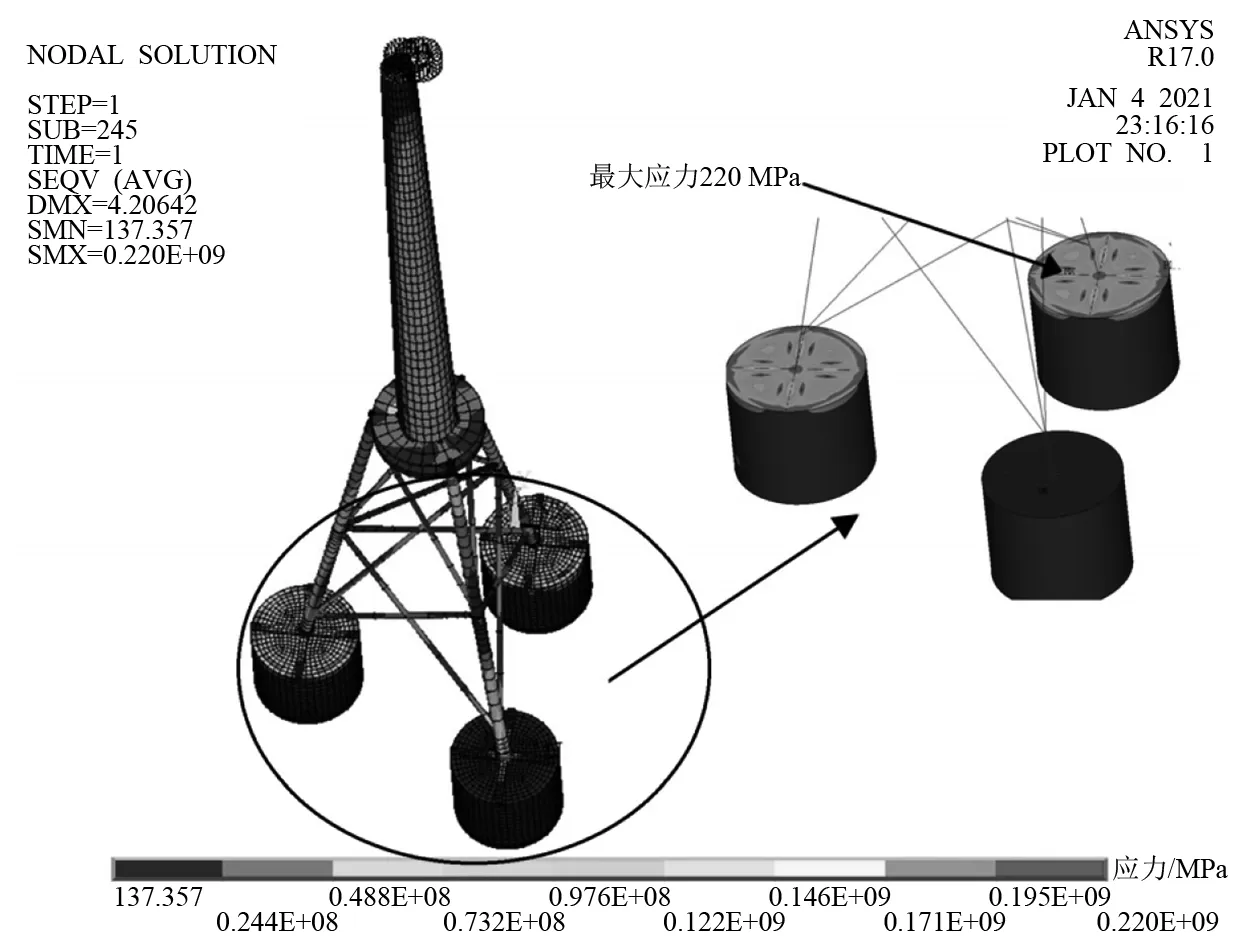
图7 五十年一遇极限工况下最大结构等效应力

3.3 地基沉降

在实际工程中，在风机基础施工前，土体已经基本完成自重固结沉降。在有限元计算中，土体的自重作用会引起土体的压缩。因此，为了确定由基础安装产生的地基沉降，需要求出基础及风机安装前后地基的沉降差[17]。土体在基础及风机安装前后随深度变化的沉降量及沉降差如图8所示。由图8可知，基础及风机安装后筒内土体最大会产生0.431 m的沉降。由于天然淤泥和淤泥质土层所受的有效上覆压力较小，因此该土层的自重固结沉降比较小。由于筒内90%的土层为淤泥质土，且筒内土体只能向下压缩，因此筒内土体的沉降差幅度最大。随着深度增加，沉降差逐渐降低。深度41.89～47.89 m为粗砂层，由于粗砂压缩性较小，因此该层的沉降差幅度较小。深度47.89～65.69 m为黏土层，压缩性增大，沉降差幅度再次变大。由沉降分析结果可知，本工程所在场址的软弱土层较厚，淤泥压缩性较大，在基础设计及安装过程中，必须为这种状况预留足够的沉降量。

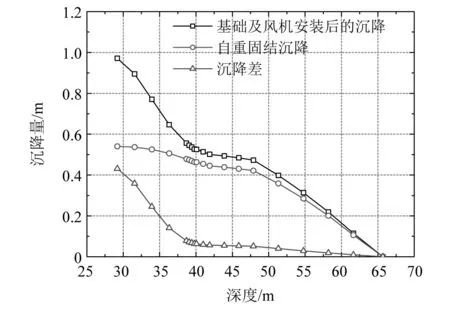
图8 基础及风机安装前后土体沉降量随深度变化

3.4 筒基承载力校核

采用有限元软件计算载荷与位移关系是通过寻找外力与内力平衡的迭代过程，迭代程序需要满足收敛标准才能继续运行。当所采取的载荷步长计算不收敛时，程序会自动采用二分法对步长进行折减，直至这一步收敛。若载荷步长折减至最小步长，程序依然无法从有限元方程组中找到一个既满足静力平衡又满足应力-应变关系和强度准则的解，则计算不收敛。位移突变与计算不收敛存在一一对应的关系。当载荷缓慢增大却发生位移突变或计算不收敛时，在滑动边界范围内土体处于塑性破坏状态，地基丧失稳定，此时的承载力为极限承载力[18-19]。

在结构载荷加载过程中，吸力筒盖与土体的接触压力-土体压缩位移关系如图9所示。由图8和图9可知，当土体压缩位移达0.971 m时，结构自重载荷已加载完成，此时继续加载。当土体压缩位移达1.170 m时，产生位移突变，此时施加的载荷即为极限承载力。结构实际载荷为32 183 kN，小于土体屈服时所施加的载荷48 930 kN，也小于基于式(16)算得的抗压承载力56 043 kN，筒基的承载力满足要求。由计算结果可知，基于有限元计算的载荷位移曲线法比规范法保守。

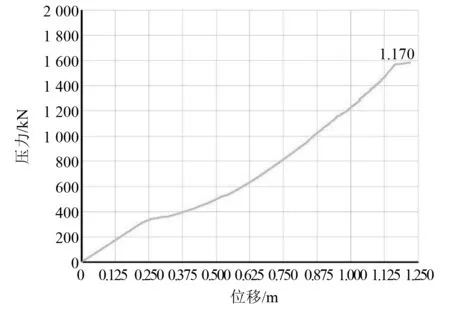
图9 接触压力-土体压缩位移

4 结 论

以中国南海某实际海上风电吸力筒导管架基础为分析对象，以50 a重现期极端工况作为载荷条件，采用三维有限元软件对吸力筒导管架的安装角度、结构强度、地基沉降和筒基承载力进行分析。结果表明：(1) 当波浪相位角为34°时，波浪会对结构产生最大的波流耦合力；当基础安装方向与浪流作用方向的相对作用角为120°时，基础所受载荷响应最小，该角度能够指导吸力筒导管架基础的安装。(2) 吸力筒导管架结构的最大等效应力为220 MPa，小于材料屈服强度。最大应力出现在背浪侧的吸力筒盖板上，在设计时可根据安装方向对壁厚进行差异性设计。根据有限元载荷位移法和规范法算出的筒基承载力都符合要求，有限元载荷位移法的计算结果偏于保守。(3) 由于软弱土层较厚，在基础及风机安装过程中最大会产生0.431 m的固结沉降，在设计过程中必须为此情况预留足够的沉降量。