单线循环固定抱索器索道运载工具力学特性研究

2022-07-18蔺鸿达

起重运输机械 2022年12期

蔺鸿达罗原徐伟纪兵陈琳

国家客运架空索道安全监督检验中心北京 100007

0 引言

客运索道主要由钢丝绳、迂回装置、驱动装置、线路支架、托压索轮、抱索器、吊具（吊椅、吊厢、吊篮）等组成。吊具通过固定式抱索器固定在钢丝绳上，由电动机通过减速器带动驱动轮旋转，驱动轮通过摩擦力带动钢丝绳做循环运动，从而达到来回运送乘客的目的。我国客运索道类型大体分为往复式索道、地轨缆车、单线循环脱挂抱索器式索道、单线循环固定抱索器式索道，在用索道为788条，其中单线循环固定抱索器式索道数量为526条，占我国索道总量的67%左右，吊椅式索道又占该类型索道数量的40%左右。

以国内某索道为单线循环固定抱索器双人吊椅式索道为例，对运载工具进行力学特性分析具有一定代表性，分析结果对客运索道在用固定抱索器和吊杆的无损检测位置以及客运索道总体设计具有指导意义。

1 主要参数

示例索道为单线循环固定抱索器双人吊椅式索道，其水平距离为791 m，斜长为811 m，高差为211 m，速度为1.25 m/s，吊椅70个，运量600人/ h，

2 运载工具的形式及固定抱索器结构原理

本文所研究的客运索道载人装置如图1所示，该装置主要由抱索器、吊架、吊椅、保护架等构件组成。

图1 客运索道的载人装置

抱索器是客运索道中最重要的受力部件，通过抱索器，吊椅与运载索一起运动，同时它还要承受乘客和载人装置的全部质量。如果抱索器出了问题，将导致吊椅从运载索上脱落，造成严重的人身伤亡事故，故对抱索器的研究是客运索道设计的重要内容。

目前国内在用单线循环固定抱索器式索道所采用的抱索器为弹簧式固定抱索器，其结构如图2所示，这种抱索器主要由外抱卡、内抱卡、芯轴、碟形弹簧、弹簧罩等部件组成。弹簧式固定抱索器采用的是蝶形弹簧，位于压盖与心轴之间（见图2），主要用于储存载荷能量，以保持恒定的抱紧力。弹簧先将力传给芯轴，芯轴将力传给顶杆，顶杆再将力传给内抱卡，实现内外抱卡的夹紧。

图2 抱索器的结构原理

蝶形弹簧最大工作负荷下单圈变形量在800 N/mm左右，且具有1.5 mm左右的伸缩量和3 mm左右的调整量。这样可根据运载索的直径变化进行调整，使其具有适宜和恒定的抱索力与防滑力，以保证吊椅索安全、可靠的运行。

3 抱索器及吊椅应力状态的实验研究

3.1 测试方法的选用

应变片电测技术是实验应力应变分方法中应用最广泛和适用性最强的方法之一。由于所使用的传感器(应变片)具有尺寸小、质量轻、灵敏度高等优点，该方法被广泛应用于机械设备的状态监测、故障诊断及各种力传感器的制作等领域。故本实验采用应变片电测法对角山索道的抱索器及吊椅关键部件在各种载荷状态下的应力应变进行检测。

3.2 测量系统

本次实验的信号采集与信号处理系统如图3所示。被测应变信号通过电阻应变仪进行信号调理，然后由数据采集卡进行采集，再由计算机进行信号显示与存储。在本次实验中，数据采集与处理采用基于LabVIEW虚拟仪器技术。

图3 信号采集与信号处理系统图框图

3.3 运载工具力学特性实验研究之测试点位置的选取

国外相关研究中，对客运索道运载工具力学特性的实验研究较多，国内对索道的试验研究工作开展较少缺乏针对运载工具的实验数据。

为了深入研究索道运载工具的真实应力状态，采用应变片测量技术，对角山索道的抱索器及吊杆在各种载荷状态下的应力进行了检测。吊杆上选择了6个测试点，图4为测点位置；考虑到粘帖应变片的可行性，分别在抱索器内、外抱卡的表面各选择了1个测试点，图5为抱索器内、外抱卡测点位置。

图4 实测现场及测点位置

图5 内、外抱卡粘贴应变片位置

3.4 应力波形分析

3.4.1 吊椅空载时抱索器抱紧与松开过程的测点信号变化

图6 为吊具空载时抱索器拧紧过程中外抱卡与内抱卡测点的信号输出波形，其中曲线8为外抱卡应变信号，曲线7为内抱卡应变信号。在抱索器拧紧力矩的作用下，内、外抱卡测点信号随着抱紧力的增加而增加，图7为抱索器卸载过程测点应变波形，内、外抱卡测点信号随着抱紧力的减小而减小，由图可见，测点应力与抱索力矩一一对应，反应了实测信号变化的真实性。

3.4.2 加载工况1

图8为第1种加载工况，即一个人乘坐吊椅时，内外抱卡及吊架上的应力变化曲线。由图可见，曲线对游客上吊椅、乘坐与下吊椅时的各个过程有明显响应。即信号的大小随加载过程的变化而变化。比较图中各曲线可发现，当游客乘坐缆车后，吊杆应力变化明显，但内外抱卡应力变化不大，说明吊椅受力对内外抱卡的应力状态影响不大。

图8 1人乘坐吊椅时的实测波形

3.4.3 加载工况2

第2种加载工况是抱索器抱索过程和吊椅上分别乘坐1人和2人时的实测信号输出波形。由图9可知，在抱索过程中，抱索器内外抱卡信号明显增加，而吊杆上的测点信号只有轻微波动，而无量值变化。当吊椅内乘坐1人时、吊杆测点信号值明显增加。乘坐2人时，吊杆信号值进一步加大，而在载荷稳定阶段，信号值非常稳定，进一步证实了实测结果的正确性。此加载过程抱索器内外抱卡信号无明显变化。

图9 抱索器抱索-吊椅加载减载全过程实测波形

当吊椅卸载时，吊杆的信号随吊椅乘坐人数的减少，逐步降低，并趋于空载时状态。而抱索器内外抱卡上的实测信号值随吊椅内乘客人数的减少略有下降，说明吊椅受力后抱卡受力状态有所变化，信号值有所降低，但下降幅度不大。

3.4.4 过压索支架时实测应力波形

图10为抱索器过压索支架时，各信号的颤振现象，虽然振幅不大，但容易引起抱索器及吊杆的疲劳破坏，同时也会使处于空中的游客产生不适感与恐惧感，由此在索道总体设计时，应尽可能减少压索支架的数量，尽量减少索道运行过程中的振动，减轻抱索器及吊杆的疲劳破坏，延长其使用寿命。

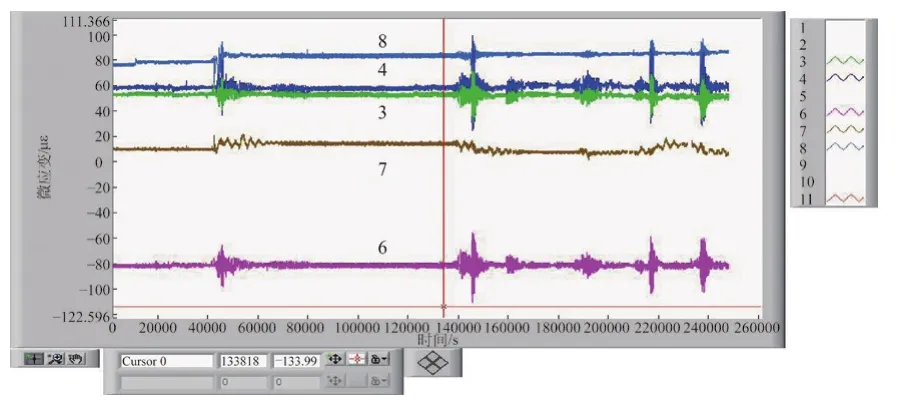
图10 过压索支架时的颤振现象

3.4.5 实验结果分析

在实验过程中，抱索器的抱索拧紧力矩为95.354 N·m。吊椅载荷：一人85 kg，另一人80 kg，仪器质量10 kg。图11为抱索器内抱卡与外抱卡在抱索、松开与吊椅受载状态时的应变变化曲线。图12为吊架上各测点的应变与应力变化，图中点1为抬起吊椅时的绝对零位，2点为吊架在承受吊椅质量时的应力，点3、点4为乘坐1人时的测点应力值，点5、点6为乘坐2人时的测点应力值。由图12可知，测点应力变化规律基本为线性。

图11 抱索器测点应变变化

图12 吊架的应变与应力变化

通过对索道抱索器与吊杆的现场实测，给出了运行过程中这些关键部件测点的真实应力状态，再以这些真实应力点为参考点，采用有限元法分析对构件整体进行力学分析，可得到更加符合实际的计算结果。

4 固定抱索器及吊杆的力学特性有限元分析

为了更全面地了解索道运载工具力学特性，考察非测量点的应力应变状态，利用有限元分析法对抱索器及吊杆的应力状态进行了计算，并以实测点的实测值为依据设置其边界条件，使计算结果更加符合实际。

4.1 固定抱索器受力分析

抱索器的简化力学模型如图13所示。为确定抱索器前端抱索卡处的应力状态，沿吊架安装中心将抱索器剖分，根据力学平衡条件，在剖分面的A点作用有与G相等的支反力RA及附加力矩MA。q为抱索力Pk与吊椅质量G在圆弧面上的压强。假设由抱索力Pk引起的压强均匀分布，沿着抱卡圆弧面，其各方向合力之和为0。

图13 抱索器力学模型

由于运载索是柔性的，在平衡状态下MA很小，故在计算过程中可忽略MA的影响。

4.1.1 内抱卡应力与应变分析

1）内抱卡应力分布

图14a为无损检测过程中内抱卡经常出现裂纹的位置，图14b、14c为内抱卡的米塞思应力分布云图，在内抱卡卡身与抱卡圆弧面的几何形状过渡区，分布着最大应力362 MPa，属于内抱卡的高应力区。在该区域内应力梯度也很大，说明该处应力集中比较严重，易产生疲劳裂纹，实际工作中，无损检测结果与有限元分析结果相吻合。其余位置的应力为40～120 MPa之间，卡身处应力更低。

内抱卡的材料为35CrMo，其屈服强度为950 MPa，可见在高应力区安全系数小于5，所以需要对内抱卡的结构进行进一步的合理设计，提高它的安全系数。

2）内抱卡位移分布

图15为内抱卡的位移云图，内抱卡最大位移区域位于抱卡的两个翼端，由于该处刚度较低，最大位移为0.108 mm。

由图14b、14c与图15可知，抱索器抱索部位的应力主要集中在中部，而位移则出现在边部，故应对抱索器钳口的长度应进行合理的设计。

图14 抱索器的应力云图

图15 内抱卡位移云图

4.1.2 外抱卡应力与应变分析

1）外抱卡的应力分布

图16为外抱卡的应力分布云图，其应力范围为23～139 MPa，最大应力为209 MPa，位于钳口内表面的应力集中区域。外抱卡的材料为35CrMo，其屈服强度为950 MPa，其安全系数也小于5，需要改善应力集中情况。

图16 外抱卡应力云图

2）外抱卡的位移分布

由图17可知，外抱卡的最大位移量为0.144 mm，位于外抱卡钳口中部的外侧圆弧表面。

图17 外抱卡位移云图

4.1.3 芯轴（顶杆）

1）芯轴（顶杆）的应力分布

由图18可知，顶杆应力分布均匀，主要分布在59～78 MPa。其最大应力点位于与内抱卡接触的端面上，是由于加载引起的局部应力，最大应力值为90.5 MPa。顶杆的材料为40Cr，其屈服极限为1 100 MPa，顶杆的安全系数远大于5，满足安全要求。

图18 芯轴（顶杆）的应力云图

2）芯轴（顶杆）的位移分布

图19为顶杆的位移分布情况，顶杆的最大位移量为0.077 32 mm，位移方式为沿轴线压缩变形，由于位移量较小，不会影响其正常使用。

图19 芯轴（顶杆）的位移云图

4.2 吊杆受力分析

吊杆是抱索器与吊椅的连接件，其强度指标非常重要。吊杆的几何形状如图20所示，是一个截面为矩形的空心平面弯曲杆。正方形截面的几何尺寸为75 mm×75 mm，壁厚5 mm。吊杆承受吊椅加乘客的重力，吊椅总重量为2 500 N，作用于吊架的下端，见图21。

图20 吊杆三维实体

图21 吊杆的受力

1）吊杆应力分布

图22为吊杆的应力分布云图，杆的最大应力值为53.4 MPa，位于拐弯处。吊杆的材料为40Cr，其屈服极限为1 100 MPa。其安全系数远大于5，满足安全要求。

图22 吊杆的应力云图

2）吊杆的位移分布

图23为吊杆的位移分布。吊杆的最大位移区域位于下端面，即与吊椅的连接处，其最大位移量为5.224 mm，该位移量为吊椅系统中位移最大的构件。

图23 吊杆的位移云图

4.3 有限元分析结果与实验结果的对照

将粘贴应变片部位面上所有节点的应力提取出来，取平均值，即得到有限元结果。表1为在乘坐2人的情况下得到的实测值与有限元值的比较。由表2可见，测点的有限元分析结果与实测结果比较吻合。

表1中相差最大的点是吊架上的测点3，实测值与计算值的误差为8.8%。分析产生误差的原因主要是测点与有限元分析结果的取点不完全重合，同时有限元力学模型的简化，使计算工况与实际工况存在一定差距，也会引起一定的计算误差。

表1 有限元结果与实验结果对比

5 客运索道吊椅的模态分析

5.1 计算结果分析

图24为吊椅的5阶模态，第1阶固有频率为吊椅沿X轴方向摆动，频率为2 Hz，最大振幅为6.228 mm，乘客会感到座椅的前后摇晃。第2阶振型为沿Z轴的摆动，频率为4 Hz，座椅扶手处位移6.462 mm，乘客会感到座椅左右摇晃。第3阶振型为沿Y轴的上下振动，频率为9 Hz，脚蹬处位移量21.86 mm，乘客的腿部会随座椅的振动而来回弯曲。第4阶频率为12 Hz，吊椅的高阶振型主要表现为复合振动，振幅最大位置在刚度最低的脚蹬处。吊椅的第5阶频率为14 Hz，围绕Y轴的转动振动，乘客会感觉到左右扭动。

图24 吊椅的5阶振型

吊椅的各阶频率、最大振幅、振型见表2，分析结果表明，在第1、2阶固有频率处，吊椅本体位移较大，而对应于高阶频率，脚蹬处的位移最大，说明吊椅保护架整体刚度较低，易于诱发振动。

表2 吊椅的1～5阶固有频率及振型

5.2 风载的影响

在实际工况下，风载荷对索道的运行具有不可忽视的影响，特别是索道的吊椅在横向风力的影响下会产生摆动。如果风力过大，会使吊椅产生较大的振幅，将直接影响到乘客的安全，在极端情况下，索道将无法安全运营。

图26为横向风对索道的作用效果，即风载荷使索道产生沿着X轴方向的舞动。势必会使吊椅产生对称于Z轴的摆动，若吊椅固有频率与运载索舞动频率重合，将导致吊椅的激烈振动。由吊椅安装方式可见，吊椅的迎风面为侧面，在横向风作用下应该产生对称于Z轴的摆动。由吊椅的模态分析结果可见，第1、2阶固有频率的振型主要表现为吊椅的前后摆动，X方向的最大位移为1.676 mm，而且作用在刚度最小的脚蹬处。3～5阶固有频率的振型为复合振型，但对称于Z轴的最大位移量都较小，第3阶位4.794 mm，第4阶位5.604 mm，作用在脚蹬处。加之运载索舞动频率较低，一般在0.1～3 Hz。若仅从吊椅动态特性分析结果考虑，在横向风的作用下吊椅不会产生共振。然而风载是复杂多变的，分析索道及吊椅在风载作用下的动态特性，依然是一个重要的研究课题，有待于做更深入地理论分析与实验研究。