相依竞争失效模型下细纱机性能退化对成纱质量的影响

邵景峰，董梦园

(西安工程大学 管理学院，陕西 西安 710048)

棉纺织品是当今世界最受欢迎的服用和家用织物，但其品质因受设备、质量控制等的制约，不同国家和地区棉纺织品品质相比差距较大。细纱机作为棉纺过程中的关键设备，其性能直接决定了纱线成品的品质。

细纱机作为一种大型复杂机电一体化设备，其内部结构复杂、加工工况多变、器材专件繁多，在整个纺纱过程中，易受温度、湿度、振动等多因素的交互作用致使其性能退化，最终对纱线的质量指标造成严重影响，因此，如何在保障细纱机可靠性前提下探讨其对纺纱质量的影响，是一个亟待解决的问题。

已有研究主要集中在可靠性的分布规律、指标构建和故障频率预测方面。例如：He等[1]利用流体力学软件对细纱机的运动模拟和表征使纱线性能得到了提高；Chen等[2]在分析细纱机系统和子系统故障次数的基础上，利用蒙特卡罗仿真模型提出了细纱机可靠性预测的仿真方法，而且将可靠性增长系数与蒙特卡洛仿真模型相结合，建立了细纱机可靠性预测模型；Cui等[3]从牵伸系统的改进出发以提高成纱质量，研究了常规牵伸系统与改进型牵伸系统的不同之处，以及工艺参数对细纱机的影响；宋晓亮等[4]研制了一种光电反射式故障诊断器，与环锭细纱机的断纱检测系统结合应用，监测到了钢丝圈的运动轨迹，解决了细纱机运行规律的变化对纱线断纱的监测问题；杨敏等[5]研究了原材料集聚纺纱线的结构及其对成织物质量的影响，分析了不同原材料的结构特征对纱线性能的直接影响；朱艳萍等[6]利用改进的小波算法，在原料、工艺配置以及设备零部件的更换方面进行成纱质量的控制，有效解决了细纱机罗拉故障中产生混频的问题；邵景峰等[7]的研究实现了对细纱机成纱质量的多工序控制；魏艳红等[8]针对细纱机的牵伸元件配置问题，研究了不同的元件用材参数对成纱质量的影响等。

随着对于细纱机这种大型复杂设备研究的深入，细纱机构造复杂造成数据采集困难，工作环境复杂多变造成自身评估的随机性问题变得越来越复杂，而基于随机过程的性能退化模型的构建对于问题的解决提供了方法基础，例如：Si等[9]利用对Wiener模型进行了深入的研究以用来描述退化轨迹，针对模型中的随机参数分别进行了理论推导和验证，给出了剩余寿命分布和可靠性函数解析形式；Li等[10]通过对系统或产品性能退化信息易受到随机误差的影响，提出了具有测量误差的Wiener过程退化模型，推导和验证了其模型误差对性能退化模型的影响；牛一凡等[11]通过对利用神经网络的方法构建退化指标，建立了多阶段的Wiener过程模型，解决了大型设备寿命预测和可靠性评估困难的问题。

可见，已有研究主要集中在性能退化建模、寿命分布以及可靠度推导应用方面，而且目前也已经解决了细纱机可靠性分析、成纱质量预测以及器材专件对成纱质量的影响问题，但还存在细纱机性能退化对成纱质量指标的影响问题尚未彻底解决。因此，本文构建了基于Wiener过程细纱机性能退化模型，并利用Weibull分布对性能突发失效过程进行预测，使细纱机的设备可靠性达到提高纱线合格率的要求。

1 成纱质量关键指标选择

按照纱线质量国家标准，在细纱工序，表征棉纺质量的指标主要有：质量偏差、棉结杂质粒数、条干均匀度、粗节、细节、毛羽、单纱断裂强度、断裂伸长率等[7]。在此基础上，借助咸阳纺织集团的“纺织厂生产信息管理系统”，从中选取相关的棉纺生产数据，进行棉纺质量指标关系的聚类分析，其结果如图1 所示。

图1 棉纺质量指标的聚类结果Fig.1 Clustering results of abnormal cotton spinning quality index

由图1可知，在整个棉纺过程中，条干不匀、粗节、细节、毛羽以及断裂强度和断裂伸长率6个指标易受各类异常因素的影响而表现显著，其中单纱断裂强度最为显著、其次依次为断裂伸长率、毛羽、粗节。这其中的主要原因在于这6个指标之间的相关性最高，而且呈正相关关系(如单纱断裂强度与断裂伸长率之间)。现以最常用的纱线品种JC7.29 tex精纺棉纱为例，从上述“纺织厂生产信息管理系统”数据中，选取得到如表1所示的28个试样数据，进一步对比分析条干不匀、粗节、细节、毛羽、单纱断裂强度、断裂伸长率6个指标的关联关系。

通过表1可知，在数据归一化处理的基础上，对条干不匀、粗节、细节等6个指标之间的关系进行仿真，得到如图2所示的结果。

表1 JC7.29 tex纱线质量波动试样数据表Tab.1 Sample data of JC7.29 tex yarn quality fluctuation

由图2可见，品种JC7.29 tex的成纱过程中，纱线的粗节、毛羽、单纱断裂强度3个质量指标受异常因素影响波动表现最为显著，这一结果与图1所示的结果一致。为此，可将粗节、毛羽、单纱断裂强度3个指标视为判断异常因素影响成纱质量波动的关键指标。

图2 JC7.29 tex纱线质量指标关系仿真结果Fig.2 Simulation results of yarn quality index of JC7.29 tex yarn

2 细纱机故障及其对成纱质量的影响

根据纺纱工艺原理，可将细纱机的常见故障分为如表2所示的2类。

由表2可见，细纱机的故障，一方面是由外部作用导致的突发失效模式，如电动机损坏、装置损坏、罗拉头断裂等，因为细纱机在整个成纱过程中处于不间断的连续工作状态，在性能退化的同时可能存在某一时间突然出现功能完全丧失的情形[12]，从而导致细纱机性能突发失效、纺纱过程终止，致使纱线断裂；另一方面是自身性能退化导致的失效模式，如前胶辊损伤、钢丝圈跑道磨损、前罗拉头发热等，而这种突发失效将会影响纱线的结构，容易导致成纱质量特征值发生突变。因此，无论哪种故障，都会直接影响成纱质量，特别是当细纱机的退化严重时，退化部位在牵伸过程中不能正确地控制成纱纤维，导致纱线质量指标突变或整个纺纱过程中断。

表2 细纱机常见故障模式Tab.2 Common failure modes of spinning frame

3 细纱机退化过程表征

3.1 性能退化参数筛选

细纱机的性能退化过程具有多种退化过程的特点[13]，正是这个特点，意味着并非所有的数据都能表征细纱机的性能退化。因为细纱机性能参数的变化，反映的是细纱机自身运行状态的变化，不同的参数对于细纱机性能变化的敏感程度不同，而且参数对细纱机的性能变化越敏感，则其变化幅度越大，同时参数权重越大，在性能退化中所占比重越大，反之越小。当然，从根本上讲，对一些不敏感的参数而言，随着细纱机性能的退化，其并不会出现较大波动。

为了筛选细纱机性能退化的参数，特引入敏感度、相关度、重要度3个判断标准，以实现细纱机性能退化的可靠性评估。

3.1.1 敏感度

现定义细纱机台数为n，第j个参数的变化幅度为cj，即敏感度，在失效监测范围内的最大值、最小值分别表示为Cmax和Cmin[14]。

(1)

3.1.2 相关度

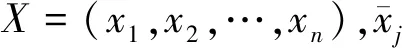
(2)

3.1.3 重要度

利用序关系分析法[15]，对细纱机性能退化的特征参数yi(i=1，2,…，n)进行重要度的比较。在式(3) 的基础上，对特征参数的重要度排序，可得到第j个特征参数的重要度pj。

(3)

(4)

由于仅单一参数标准不能很好地表征细纱机的性能退化，故将这些参数进行综合考虑，并通过权重赋值融合成综合指标，以形成综合退化指标。

由此，将上述敏感度cj、相关度sj、参数重要度pj进行综合考虑，得到综合筛选参数的标准hj。

hj=cjsjfj

(5)

根据纺纱工艺原理，为了表征细纱机性能退化状态，选择综合权重hj>0.5的参数作为细纱机性能退化的关键参数。

3.2 性能退化指标建立

令筛选的关键参数个数为m，对应的细纱机状态特征集为X={x1,x2,…,xm}。现将状态特征集X={x1,x2,…,xm}进行归一化处理，得到每个参数xj对应的权重wj。同时，将wj与对应的xj进行融合，并计算得到第k个细纱机的综合退化指标yk。

(6)

(7)

3.3 性能退化过程的统计

在成纱过程中，细纱机通常会伴随着一个或多个部组件性能指标的退化，这意味着细纱机的性能退化是一个平稳退化。由于Wiener 过程具有良好的统计分析特性和物理意义能够描述非单调的退化过程[16]，这为细纱机性能退化的统计分析带来了便利，而且更加符合实际。

为此，利用Wiener过程来表征细纱机的性能退化过程，具体如下所示。

Y(t)=Y(0)+μt+σB(t)

(8)

式中：Y(0)是初始时刻的综合性能退化量；μ是飘移系数；B(t)是标准布朗运动；σ是扩散系数。

假设细纱机性能失效阈值为ω，寿命为T，则通过式(8)，细纱机的寿命T可定义为

T={t:Y(t)≥ω|Y(0)<ω}

(9)

由式(9)可见，细纱机的寿命T服从逆高斯分布，进而寿命T的概率密度函数fT(t)和可靠度函数Rw(t)可分别表示成如式(10)、(11)所示的形式。

(10)

(11)

式中Φ(·)为标准正态分布函数。

通过式(10)、(11)，可对未知参数μ和σ2进行计算并得到估计值。

3.4 性能突发失效过程预测

由于威布尔分布(Weibull分布)具有良好的适应性，可以拟合不同类型的分布[17]，这为细纱机突发失效过程的预测提供了可能。为此，设细纱机t时刻退化量为x对应的突发失效故障概率为λc(t|x)，则根据威布尔分布建立如下关系式。

(12)

通过式(12)为得到的突发失效时间tc的概率密度函数fc(t|x)和累积分布函数Fc(t|x)。

(13)

Fc(t|x)=P(t>Tc|x)=1-exp(-(tx/a)b)

(14)

由此，细纱机在t时刻性能突发失效的可靠度Rc(t|x)可以表示成如下关系式[18]：

(15)

3.5 细纱机性能相依竞争失效模型

3.5.1 竞争失效模型构建

假定细纱机在性能退化过程中突发失效与退化失效不相关，那么可以将2种过程视为简单的串联系统，其可靠度Ri可以表示为

Ri=Rw(t)Rc(t)

(16)

但这种串联并不适合细纱机的工作实际，因为细纱机性能的突发失效与退化失效之间存在一定的相关性。为了解决这一问题，利用Copula函数在相关性研究方面的灵活性，构建了基于Copula函数的细纱机性能相依竞争失效模型，对不同过程间的相关性进行构造[19]。

设FY(t)表示基于维纳过程的细纱机自身性能退化过程函数，FX(tc)表示基于威尔分布的细纱机突发失效过程函数，则{FX(t),FX(tc)}的联合分布函数可以用式(17)表示：

H(Y(t),X(tc),θ)=C(FY(t),FX(tc),θ)

(17)

同时，{FX(t),FX(tc)}的联合密度函数为

h(x,t,θ)=c[FY(t),FX(tc),θ]FY(t)FX(tc)

(18)

在此基础上，根据AIC 准则，在常见的Gaussian Copula、Clayton Copula、Frank Copula和Gumbel Copula函数等函数中选择最优的函数进行细纱机性能的突发失效与退化失效相关性分析[20]。

3.5.2 模型参数估计

假设性能指标在初始时刻t0的退化量Y0=0，则ΔYi=Yi-Yi-1为细纱机在时刻ti-1和ti的退化增量，Δti=ti-ti-1为时刻ti-1和ti的时间间隔，则由Wiener随机过程的性质可得：ΔYi～N(μΔti,σ2Δti)。由此，基于Wiener随机过程的细纱机性能退化模型参数的似然函数如式(19)所示。

(19)

在式(19)的基础上，对μ和σ2进行求偏导计算。令偏导为零，则可以对方程进行求解得到μ和σ2的估计值分别为：

(20)

(21)

结合式(20)、(21)，将综合指标退化数据代入式(10)、(11)，可得到细纱机性能退化过程中的寿命密度函数和可靠度。

记录n台细纱机在性能突发失效时间(Tc1,Tc2，…,TcN)对应的性能退化量为(x1,x2,…，xN)，则根据式(14)可以得到似然函数：

(22)

目前，基于Copula 函数的参数估计方法相对较多，但大部分计算过程复杂，再加之细纱机性能退化模型复杂，未知参数较多等问题，使得常见的参数估计方法不适合细纱机性能的参数估计[21]。

基于贝叶斯理论的Gibbs算法为该参数估计提供了可能[22]。由此，将2个过程所有的未知参数定义为γ，这样γ可视为一个n维变量，即γ=(γ1,γ2,…，γn)，与其对应的先验分布为p(γ1,γ2,…，γn)。由此，基于 Gibbs的细纱机性能参数估计过程如下所示。

1)设定马尔科夫链的初始值γ(0)=(γ1(0),γ2(0),…，γn(0))；

2)从条件概率密度p(γn|γ1(0),γ2(0),…，γn-1(0))抽取γ1(1)；

3)重复步骤2)，直到从p(γn|γ1(0),γ2(0),…，γn-1(0))抽取γn(1)，完成一次迭代；

4)重复步骤2)、3)迭代m次，可以得到样本γ(m)=(γ1(m),γ2(m),…，γn(m))。

4 模型验证

4.1 参数选择

结合表2中的故障模式，从细纱机自身、电气系统两方面入手，选择细纱机运行过程中的性能参数、故障数据以及工艺参数，其中主要包括捻度、转速、钢领板上升螺距和下降螺距、管纱总高度、钢丝圈绕钢领环的旋转角等，并将其作为细纱机性能退化的原始性能参数。经整理，得到的性能参数如表3所示。

表3 细纱机性能参数Tab.3 Performance parameters

4.2 综合指标建立

结合敏感度、相关度、重要度3个标准，对细纱机性能退化参数进行筛选和量化评估。

现选取50台细纱机的运行数据作为样本集，以30台细纱机作为筛选和量化评估的样本库，以 20台细纱机作为测试，验证综合指标构建的有效性。经聚类分析，得到的3个标准和综合标准权重结果如图3所示。

由图3可见，在敏感度标准中，第4个参数(锭子速度)的计算结果最为显著，依次为第5个参数(前罗拉转速度)、第7个参数(前罗拉线速度)、第9个参数(牵伸倍数)、第10个参数(电动机功率)和第13个参数(钢领板上升速度)，在相关度标准中，除了第6个参数(中罗拉转速度)外，其他参数之间存在强相关性，而且锭子速度、前罗拉线速度、捻度、牵伸倍数之间关系最为显著。在重要度标准中，锭子速度的计算结果最为显著，依次为前罗拉转速、前罗拉线速度、牵伸倍数、电动机功率和钢领板上升速度。

图3 细纱机性能参数筛选Fig.3 Selection of performance parameters.(a) Sensitivity;(b) Correlation;(c) Importance;(d) Weight

在此基础上，按照敏感度、相关度、重要度3个标准，在数据归一化处理的基础上计算得到选取最显著的6个参数锭子速度、前罗拉转速、前罗拉线速度、总牵伸倍数、电动机功率、钢领板上升速度的权重分别为0.426 8、0.217 8、0.082 9、0.072 5、0.095 8、0.104 2，并将这6个参数权重其作为计算综合指标融合的权重。根据权重计算出的综合指标，从20台测试所用细纱机中选择综合指标最为显著的5台，对其变化趋势进行拟合，得到如图4所示的结果。

图4 综合指标变化趋势Fig.4 Change trend of comprehensive indicators

4.3 模型优化

(23)

(24)

经检验，得到的退化数据与预测数据拟合优度系数R值为0.945 7，即综合退化指标的拟合程度为94.57%。这一结果说明构建的细纱机性能相依竞争失效模型对综合退化指标的拟合程度较好。

结合图4，发现5号细纱机在成纱过程中有一段时间(10～20 d之间)其性能退化发生了突变。此时，需借助相依竞争失效模型对5号细纱机进行跟踪，在获取监测数据的基础上，将数据代入式(15)，计算得到其可靠度，得到图5所示的曲线表明细纱机突发失效在监测时间间隔内平稳下降。

图5 突发失效可靠度曲线Fig.5 Sudden failure reliability curve

由于细纱机突发失效和退化失效之间具有相关性，因此在图5的基础上还需利用Copula 函数分析细纱机性能突发失效以及自身性能退化的影响，利用AIC准则进行检验[24]。得到的4种常见的Copula 函数的结果分别为：Gumbel Copula、Frank Copula、Clayton Copula、Gaussian Copula函数AIC值分别为-22.43、-22.29、-12.65、-21.12，按照AIC值越小拟合效果越好的原则，选择Gumbel Copula函数进行相关性退化建模，得到的概率密度函数和联合分布函数分别如图6、7所示。

图6 概率密度函数Fig.6 Probability density function

图7 联合分布函数Fig.7 Joint distribution function

图6、7显示的结果表明5号细纱机性能退化失效和突发失效之间具有相依性。为此，利用式(18)所示的可靠度函数，将两个过程进行相依可靠度分析，得到的不同结果的可靠性曲线结果如图8所示。当突发失效以及性能退化失效两者具有相关性时细纱机的可靠度如图8中Rc所示，细纱机真实性能故障数据评估的可靠性曲线如图8中RI所示，Rg为5号细纱机仅考虑性能退化失效的可靠性曲线。Rh为5号细纱机仅考虑突发失效的可靠性曲线。由图8可知，曲线Rc与RI之间拟合度最高。这一结论说明：构建的基于Gumbel Copula 函数的细纱机相依竞争失效模型，其准确度较高，而且能够较好地描述5号细纱机的性能退化轨迹。

图8 不同模型可靠性曲线Fig.8 Reliability curves of different models

5 建模前后关键质量指标的对比分析

将构建的细纱机性能相依竞争失效模型应用于细纱机的可靠性评估过程当中，同时对比分析应用模型前后，对细纱机可靠性降低的时间进行预测，在这个时间周期内对细纱机进行检修，对比分析检修前后对选取成纱质量指标(粗节、毛羽、单纱断裂强度)的变化情况，其在应用模型前后的成纱质量指标如表4所示。

表4 纱线质量指标数据对比Tab.4 Comparison of yarn quality index data

利用检修后的指标值进行比较，得到各指标变化的百分数。粗节减少了10.09%，毛羽减少了23.5%。单纱断裂强度提升了4.26%。这一结论表明：细纱机性能相依竞争失效模型不仅提高了单纱断裂强度，降低了毛羽值，减少了纱线的不合格率，同时又保证了细纱生产过程中的设备参数的要求，达到了对细纱机的设备可靠性的要求。

6 结 论

从细纱机性能退化对纱线质量波动的因素出发，选取细纱机性能退化对成纱质量影响的主要质量指标。同时，选取了粗节、毛羽、单纱断裂强度作为判断细纱机性能退化影响成纱质量的关键指标。进而，分析了细纱机性能退化的主要原因，将影响细纱机性能退化的模式分为由于外部作用导致的突发失效模式和由于自身性能退化导致的失效模式，引入敏感度、相关度、重要度3个标准，对细纱机性能退化参数进行了筛选和量化评估。

在此基础上，构建了基于Wiener过程细纱机性能退化模型，同时利用Weibull分布对性能突发失效过程进行预测，研究了细纱机性能退化失效与突发失效之间的相依性，构建了一种基于Copula函数的相依竞争失效模型，并利用Gibbs算法进行了参数估计。最后，通过细纱机性能相依竞争失效模型的应用，粗节减少了10.09%，毛羽减少了23.5%。单纱断裂强度提升了4.26%，结果表明：细纱机性能相依竞争失效模型不仅提高了单纱断裂强度，降低了毛羽值，减少了纱线的不合格率，达到了对细纱机的设备可靠性的要求。

FZXB