地震作用下三层钢框架结构的弹塑性响应分析
2022-07-18田钦胡振秋霍振坤黄发明
田钦,胡振秋,霍振坤,黄发明
(1.南昌大学工程建设学院,江西 南昌 330031;2.江西省近零能耗建筑工程实验室,江西 南昌 330031)
近年来,钢结构因其抗拉强度大,刚度适中、耗能显著,并且在加入混凝土后可提高混凝土的抗拉强度,适中的配筋率可避免混凝土的脆性破坏,减小混凝土的收缩、徐变等优点而被广泛应用于各类桥梁、房屋结构中,尤其适用于构件发生较大变形处。因此,高层钢框架结构的抗震问题已逐渐成为建筑工程领域重点探讨和关心的问题[1-2]。目前对钢结构进行地震作用下的弹塑性时程分析时,主要有多尺度模型和板壳模型。多尺度模型是一种新兴模型,计算效率较高。该计算模型将一个截面划分为多个微小面元,再将各面元通过积分、胡克定律计算出整个截面的相对应力状态[3];板壳模型则因为所需的前提少,且能同时考虑动轴效应、多向应力状态以及局部屈曲等诸多影响因素,被认为现有计算精度较高的模型之一,能较为准确、客观地模拟钢结构在受到强烈地震冲击时所可能产生的损坏[4-5]。
Ge等[6]的试验和计算分析表明,当钢结构受到过大损害而产生明显应变后,多尺度模型能保证计算精度的前提下,提高计算效率,有很好的应用前景。来少平等[7]对一个复杂多层建筑结构进行多尺度模型分析,绘制出钢结构在承受地震作用下结构的动力时程曲线,研究结果表明多尺度模型能提高计算效率。另外,多尺度模型不但能准确体现各个结构的整体状态,还能准确显示各个节点在受到地震作用下所产生的应力应变。李双江等[8]对三层四跨Benchmark钢框架结构建立多尺度模型并进行在地震作用下钢框架结构的应变分析。通过分析多尺度模型、梁单元模型以及实体单元模型在地震作用下存在的差异,验证了多尺度模型在进行结构分析和计算时具有不占用过多的计算空间的优势。因此,多尺度模型可用于大型、复杂建筑结构的数值模拟分析。Zhao等[9]通过设计和建立不同板壳节段长度的钢框架结构的多尺度模型,分析不同尺寸的模型在受到地震作用后的变形情况,探讨板壳节段长度对分析结果精度的影响。研究表明多尺度模型板壳节段损伤域的数量将直接影响该模型与试验结果是否相符。潘存瑞等[10]采用多尺度模型建立多层钢筋混凝土框架结构。通过对比多尺度模型和板壳模型的弹塑性地震响应分析,证实了多尺度模型可以有效节约计算时间,并且与实际试验情况的拟合程度较好。Mahmoud等[11]采用多尺度有限元分析方法,对钢框架进行地震作用下的弹塑性反应分析,并采用UI-SIMCOR分析并对比。发现多尺度有限元分析方法能够在保证计算精确度的同时又不会增加太多的计算时间。赵中伟[12]建立了家堡交通枢纽站房的多尺度模型,在结构中选取关键点,精确模拟边界条件。研究结果表明多尺度有限元计算模型应用于复杂结构的分析计算是有效的,能兼顾计算效率和计算精度。邹国胜[13]建立多尺度模型,对结构局部节点精细化单元分析,准确模拟边界条件。研究结果表明,多尺度有限元计算模型分析耗时短、消耗计算机内存小,能显著提高计算精度。
目前,对三层钢框架的静力分析已趋于成熟,但对其动力分析结果并不多见[14]。本文通过建立三层钢框架的多尺度模型,并于钢框架底部在垂直于强轴方向输入集集地震动,提取了钢框架6个节点的塑性应变图,并对两种模型下各层的位移-时间曲线进行对比,证明了多尺度模型计算精度高,效率好,验证了板壳节段公式的合理性。
1 三层钢框架的弹塑性研究
采用有限元分析软件ABAQUS,对三层钢框架结构分别设计板壳模型和多尺度模型,在垂直于三层钢框架强轴方向输入地震动,分析并对比两种模型之间的弹塑性响应[15]。
1.1 建立有限元模型
本文采用Q235钢材,三层钢框架模型的平面尺寸如图1所示。
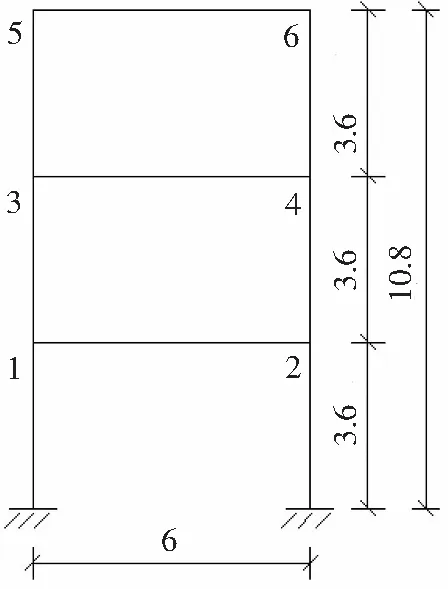
图1 三层钢框架平面尺寸(单位:m)Fig.1 Plane size of three-story steel frame (unit:m)
梁柱截面尺寸如图2所示[16]。钢构件密度ρ=7.9 g·cm-3,杨氏模量E=200 GPa,泊松比μ=0.3,屈服应变εy=1.14×10-3。分析方法采用动态隐式分析法。通过约束MPC-BEAM连接纤维单元B31与板壳单元S4R,从而建立多尺度模型,该模型中的同类单元采用Tie约束方式连接,钢结构框架的多尺度模型如图3(a)所示。板壳模型通过S4R单元进行模拟,板壳模型如图3(b)所示。
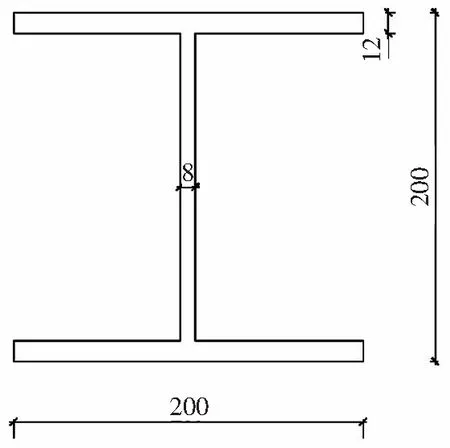
(a) 柱截面
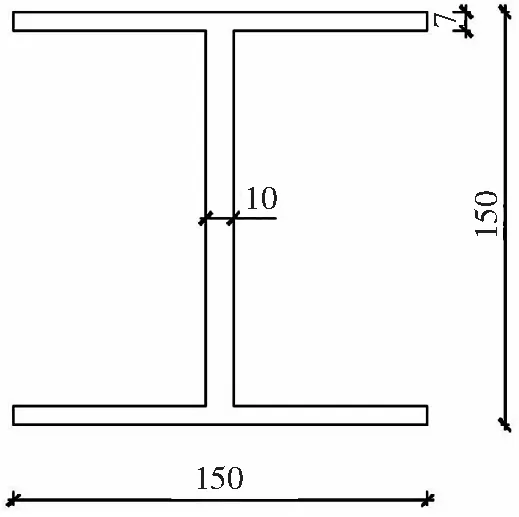
(b) 梁截面图2 梁柱截面尺寸(单位:mm)Fig.2 Cross-sectional dimensions of beam and column (unit:mm)

(a) 多尺度模型

(b) 板壳模型图3 模型示意图Fig.3 Schematic diagram of the finite element model
1.2 荷载输入
本文采用集集地震,地震动输入位置为三层钢框架底部两个参考点RP-1、RP-2。如图4所示截面强轴为z轴,集集地震波如图5所示。
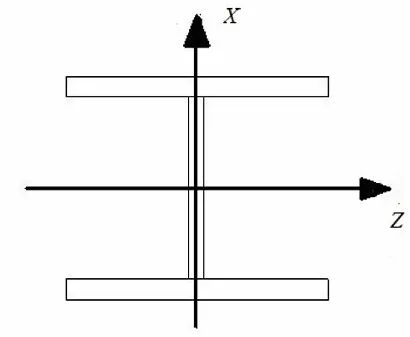
图4 截面强轴图Fig.4 Strong axis of section

t/s图5 集集地震波Fig.5 Chi-Chi earthquake wave
1.3 弹塑性有限元分析
H型钢在受到垂直于强轴方向荷载作用时,其损伤域计算长度采用以下公式[17]:
L=0.136 7x1+0.073 5+0.000 5max{0,70-x2}
x1>0.1
(1)
L=0.073 5+0.000 5max{0,70-x2}
x1≤0.1
(2)
式中:x1=N/Ny(轴压比);x2=λ(长细比)。
本文轴压比x1和长细比x2分别取0和50,通过损伤域计算式(1)、式(2),可确定多尺度模型板壳节段长度为83.5 m。为使板壳节段包含全部损伤域长度,模型中适当放长板壳节段长度,取值为155 mm,最后各层损伤域长度分别为80,85,83 mm。同理,当x1=0.2,x2=50时,节段长度为110.84 mm,最后各层损伤域长度分别为104,108,115 mm。以上结果表明数值分析结果与理论计算结果相近,损伤域长度的计算公式比较合理。
进行数值模拟后,分别得到两种模型各层位移-时程曲线,如图6所示。板壳模型与多尺度模型的各层位移-时程曲线几乎重合,误差很小。
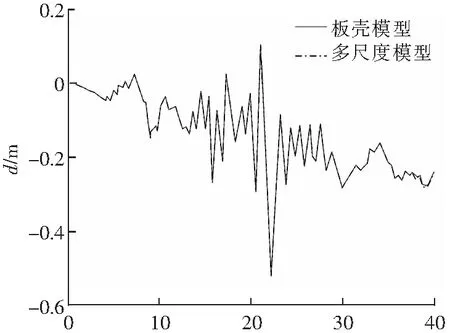
t/s(a) 一层

t/s(b) 二层

t/s(c) 三层图6 三层钢架位移-时程曲线Fig.6 Displacement-time curve of three-story steel frame
图7所示是三层钢框架结构中的6个节点(图1)局部应变云图。由应变云图可知,6个节点最大变形处的应变均已超过钢材屈服应变,但多尺度模型中的板壳节段包含了节点附近大应变的区域,从而起到与板壳模型分析节点应变相同的效果。因此,多尺度模型在一定程度上能代替板壳模型进行弹塑性有限元分析。

(a) 节点1(b) 节点2(c) 节点3

(d) 节点4(e) 节点5(f) 节点6
综合图6与图7分析的结果可知,对于H型钢柱受到垂直于强轴方向的地震荷载时,提出的板壳节段计算公式可应用于钢结构分析,两种模型的结果有较好的契合度。另一方面,多尺度模型分析时长约为3 h,但板壳模型所需时长约为5 h,多尺度模型的计算效率高。
2 结论
本文分别采用板壳模型和多尺度模型建立三层钢框架的结构模型,当地震波作用在垂直于钢框架强轴方向时,进行钢框架模型的弹塑性响应分析。基于各层的位移-时程曲线和节点应变云图,得出如下结论:
(1)多尺度模型所需分析时间约为3 h,板壳模型所需时间约为5 h,多尺度模型可显著提高计算效率且计算精度与板壳模型基本一致。
(2)基于H型钢柱提出的损伤域长度计算公式,建立三层钢框架多尺度模型,该模型中的板壳节段能包含损伤区域。
(3)轴压比分别取0和0.2,长细比取50时,通过理论公式计算损伤域长度分别为83.5,110.84 mm。在垂直于H型钢构件强轴方向的地震作用下,多尺度模型与板壳模型的计算结果基本一致,验证了多尺度模型中板壳节段计算公式的合理性。
