二维线性谐振子在不同坐标下的研究
2022-07-18郑兴荣高晓红
杨 伟, 张 杰, 郑兴荣, 高晓红, 张 郃
(陇东学院 电气工程学院,甘肃 庆阳 745000)
量子力学作为现代物理学的基础和核心理论课程,是研究微观粒子运动规律的物理学分支学科[1—2].它阐述了物质的波粒二象性,以及能量与物质的相互作用,是现代学科领域的基础,如大数据、生物科学、通信工程、电力电子、自动化和量子通信等[3—7].谐振子作为量子力学中最重要的模型之一,它的研究对于量子理论,乃至微观世界的探索至关重要.谐振子运动及其相关特性的研究, 无论在理论上还是应用上都具有重要意义.近些年,许多研究者对谐振子及其特性的大量研究趋于活跃[8—17],并且取得了一些成果,尤其是一维线性谐振子.而二维各向同性谐振子是谐振子模型中较具代表性的模型之一, 也是量子力学中的重要模型之一, 因此,谐振子及其模型的研究具有重要意义.要正确深入研究此模型, 必须分析其基态能量和波函数.
本文从两种不同的角度对此问题进行了探讨与研究, 即选用不同的坐标系(直角坐标系和极坐标系), 采用两种不同的方法(理论推导法和仿真模拟法)计算了二维各向同性谐振子的基态能量、波函数和概率密度,并对其特性做了可视化的研究与分析,包括二维谐振子的三维图形、等高线、伪真彩图.这种不同角度、不同思路的研究更有助于对抽象概念的理解与掌握.
1 研究方法及推导过程
1.1 量子力学中的二维线性谐振子
根据一维线性谐振子的原理[7—12],结合二维线性谐振子理论[16,18—19],分别在直角坐标和极坐标下进行讨论.
1.1.1直角坐标系下的二维线性谐振子 二维线性谐振子的势能函数为U=ω2(x2+y2)/2时,体系中定态薛定谔方程为
(1)
根据分离变量法ψ(x,y)=φ(x)φ(y)[15],得到二维谐振子的波函数为
(2)
式中:体系的能量E=(nx+ny+1)hω;Nnx,Nny为归一化系数,选择自然单位h=μ=ω=1(则有α=1),其表述为
(3)
Hnx(x),Hny(y)为Hermitian多项式,表达式为
(4)
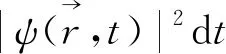
因此,根据归一化条件,可得粒子在dτ中出现的概率
Pdτ=|Ψ|2dτ,
(5)
式中:|Ψ|2=Ψ*Ψ称为粒子空间分布的概率密度;Ψ*表示Ψ的共轭复数.
1.1.2极坐标系下的二维线性谐振子 在极坐标系下,体系的定态薛定谔方程为
(6)
在自然单位(h=μ=ω=1)的情况下,利用分离变量法求解.通过对r→0和r→∞两种特殊情况进行研究[16—17],结合归一性,得到径向波函数
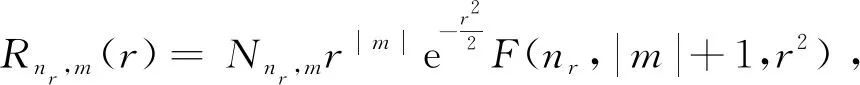
(7)
式中:Nnr,m为归一化系数,其表达式为
(8)
F(-nr,|m|+1,r2)为合流超几何函数,即
(9)
则波函数的表达式为
[sin(mφ)+cos(mφ)].
(10)
同理,根据归一化性质,得到粒子在dτ中出现的概率
Pdτ=|Ψ|2dτ.
(11)
2 仿真结果与讨论
2.1 直角坐标系下的数值仿真
根据(2)~(4)式,采用MATLAB软件,绘制直角坐标系下不同粒子数,不同能级下二维线性谐振子的波函数仿真图,得到了9种直角坐标系下的波函数网格图(图1).同时,结合二维谐振子的理论推导,得到了9种波函数图对应的9个波函数概率密度分布图(图2).
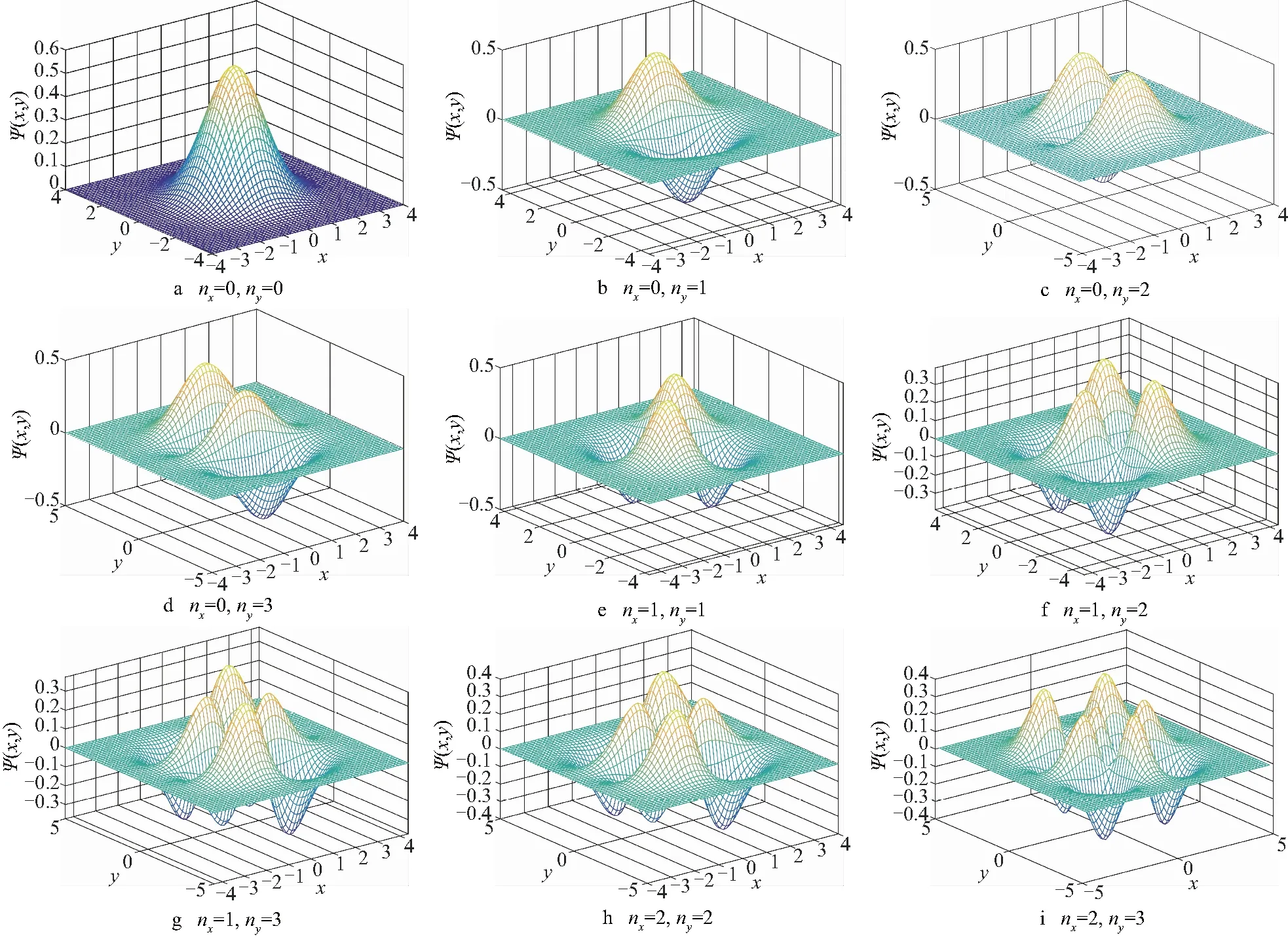
图1 直角坐标系下波函数的仿真
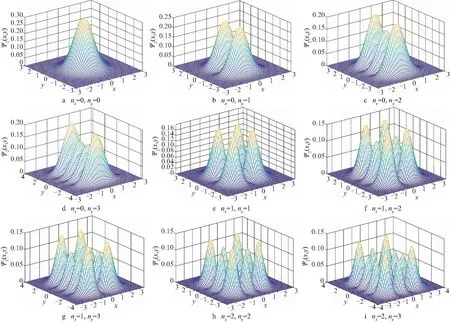
图2 直角坐标系下的波函数概率密度分布
结合理论推导,由图1和图2可以得到:在直角坐标系中,二维线性谐振子的简并度为nx+ny+1,对应的能量本征值为hω(nx+ny+1);但在nx+ny=0时,其对应的基态波函数无简并,如图1a的nx=0,ny=0;波函数与Ψ=0平面的交线数为nx+ny.一般情况下,二维线性谐振子的概率密度分布的极大值个数为(nx+1)(ny+1).图1和图2的结果和理论结果完全符合[13,18—20],很好地反映了直角坐标系下波函数及其概率密度的特性.
2.2 极坐标系下的数值仿真
根据二维线性谐振子在极坐标系下的理论推导,结合MATLAB软件,得到了极坐标系下二维线性谐振子波函数和概率密度的仿真图(图3和图4).
由图3和图4可以得到:极坐标系下,除特殊情况nr=0, |m|=0外,二维线性谐振子的简并度为2nr+|m|+1,对应的能量本征值为hω(2nr+|m|+1);波函数与平面Ψ=0的交线数为2nr+|m|.在nr=0的情况下,概率密度分布的极大值个数为2|m|.图3和图4的结果和理论结果完全符合[16,21],很好地反映了极坐标系下波函数及其概率密度的特性.
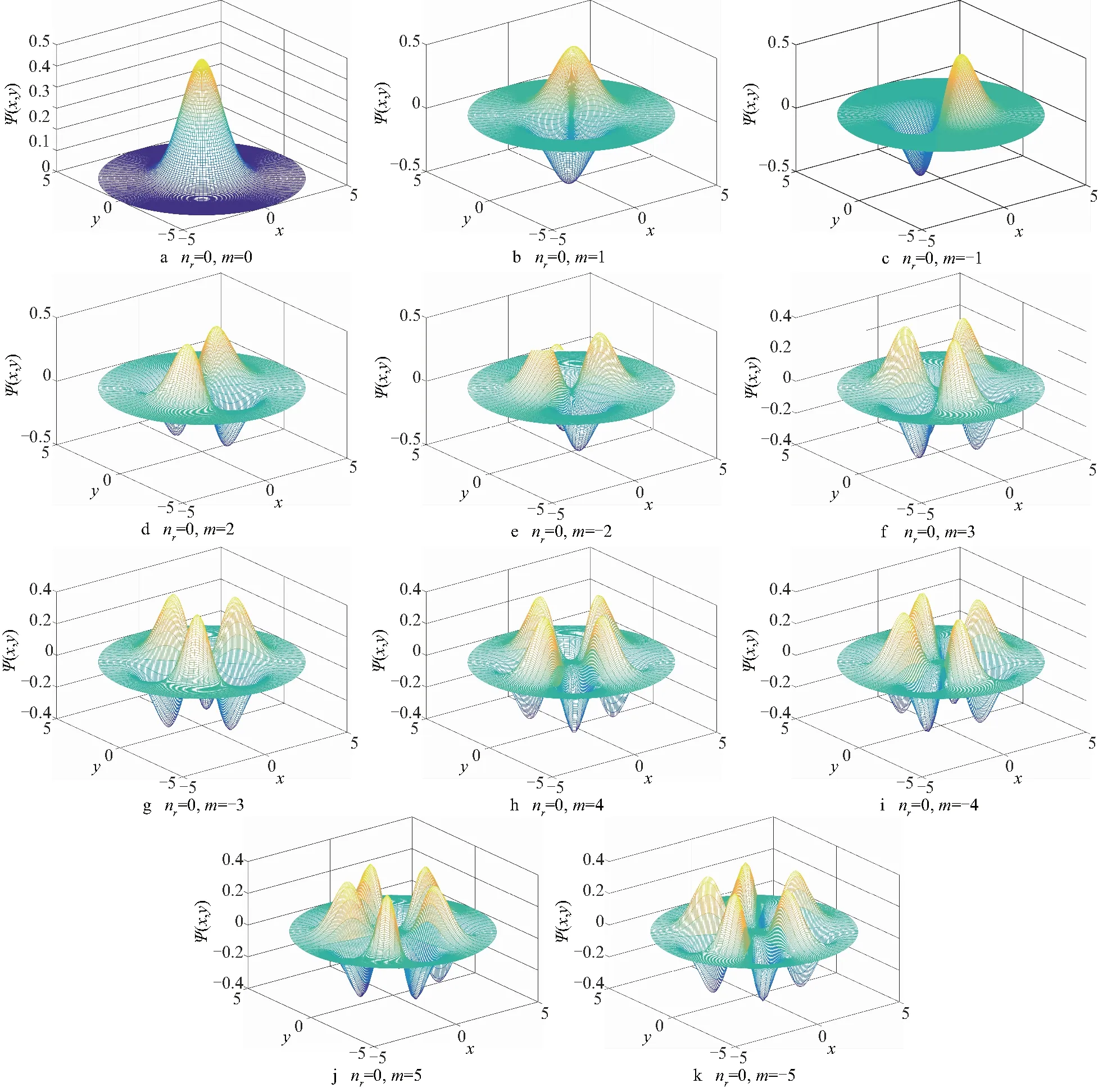
图3 极坐标系下波函数的仿真
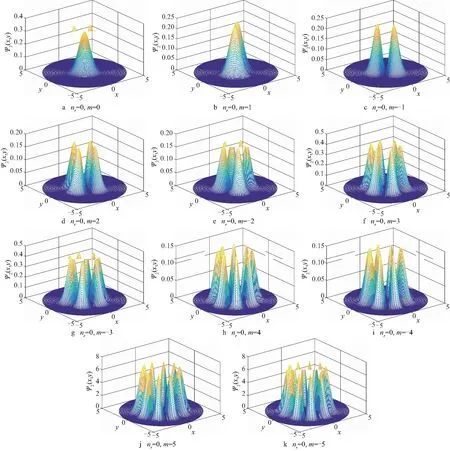
图4 极坐标系下的波函数概率密度分布
3 结论
1)在直角坐标系下,二维线性谐振子的简并度为nx+ny+1,对应的能量本征值为hω(nx+ny+1).但当nx+ny=0时,对应的基态波函数无简并;波函数与平面Ψ=0的交线数为nx+ny;一般情况下,波函数的概率密度分布的极大值个数为(nx+1)×(ny+1).
2)在极坐标系下,除特殊情况nr=0, |m|=0外,二维线性谐振子的简并度为2nr+|m|+1,对应的能量本征值为hω(2nr+|m|+1);波函数与平面Ψ=0的交线数为2nr+|m|.在nr=0的情况下,概率密度分布的极大值个数为2|m|.
3)通过与理论推导结果比较,直角坐标系和极坐标系下的仿真图形结果很好地反映了波函数及其概率密度的特性,且与理论结果完全符合.这种不同坐标系下的可视化研究结果可以相互验证,开拓了一种新的研究思路,也为其他量子理论模型的研究提供了思路.这种研究方法为理解抽象性概念提供了新的方法和思路.
