贝雷梁结构计算方法对比分析

程明明

(1.中交第二航务工程局有限公司 武汉市 430040； 2.长大桥梁建设施工技术交通行业重点实验室 武汉市 430040)

0 引言

贝雷梁原为军用产品，随着我国公路建设的发展，贝雷梁逐渐被利用在公路桥梁临时结构中。高效的周转性、较高程度的装配化以及高效的钢材截面利用率，贝雷梁结构在工程建设尤其是公路桥梁建设中发挥了重要的作用。

纵观国家标准和行业规范，均无贝雷梁设计计算针对性的标准规范，仅部分地方标准有所涉及。引用程度最高的为广州军区工程科研设计所编写的《装配式公路钢桥多用途使用手册》，以下简称《装配钢桥手册》。然而《装配钢桥手册》主要设计依据为1986年颁布的《公路桥涵钢结构及木结构设计规范》(JTJ 025—86)，以下简称《老钢桥规范》。

《老钢桥规范》采用的是容许应力法，然而现行规范均广泛采用考虑分项系数的极限状态法。如果参考现行规范对贝雷梁结构进行设计计算不免会产生歧义。

工程实践过程中，不同企业不同设计者会根据自身经验参考不同的规范以及选择不同的计算方法。本文将具体介绍分析常见的3种计算方法，并通过一系列的试验，分析对不同计算方法的差异以及缺陷。

1 贝雷梁以及设计指标介绍

工程上常见为321型贝雷(图1)，本文只针对321型贝雷进行讨论。

图1 单片321型贝雷梁结构示意图[1]

根据《装配钢桥手册》介绍贝雷梁为桁架结构，桁架的弦杆由2根10号槽钢组合而成，斜杆和竖杆由8号工字钢制成，所有杆件材质为16Mn。贝雷与贝雷之间通过销轴连接。

1.1 桁架单元杆件设计指标

根据杆件截面面积以及当时的《老钢桥规范》，装配钢桥手册得到各杆件理论容许承载力如表1。

表1 贝雷桁架单元杆件理论容许承载力[1]

其中桁架各单元在各种受力状态下不考虑压弯稳定时的承载能力。

1.2 桁架等效梁单元设计指标

工程实践中贝雷梁系由单元桁架销接而成，单元间完全依靠销轴传力，结构分析可以单元桁架为研究对象，《装配钢桥手册》将内力分为受纯弯和纯剪两部分叠加而成[1]。

根据受力分析，弯矩由弦杆承受，剪力由竖杆和斜杆。再根据杆件的容许承载力推导出桁架单元等效梁单元特性，如表2。

表2 贝雷桁架梁单元特性表[1]

2 常见设计计算方法介绍与对比分析

2.1 等效梁单元计算控制贝雷弯矩和剪力

本文定义为方法一，设计方法采用容许应力法，贝雷等效为实腹钢梁。计算贝雷梁内力时荷载组合中各分项系数均取1.0，计算所得的贝雷弯矩和剪力与表2的贝雷容许弯矩和容许剪力进行比较。贝雷以外的构件设计采用极限状态设计方法，荷载组合各分项系数均依照现行规范取值。

此方法的优点是，结构计算简便明了，贝雷设计与《装配钢桥手册》保持高度的统一。

缺点主要有两点：

(1)同一设计中容许应力法和极限状态共存，可能会产生一定混淆和理解不当。例如，重庆市地方标准《现浇混凝土桥梁梁柱式模板支撑架安全技术规范》(DBJ 50-112—2016)，该规范采用的是极限状态设计法，但其附录C 贝雷梁的承载力设计值及截面几何特性中所给的弯矩和剪力承载力设计值与本文1.2节所述的桁架等效梁单元容许弯矩和容许剪力一致。贝雷抗力设计与容许值取值一样，难免会给设计者造成一定困扰，影响设计结果。

(2)某些情况下，等效梁单元无法反映真实受力情况。《装配钢桥手册》中贝雷有特定的使用和构造要求，使用方法不当或构造不合理会导致贝雷杆件实际受力与理论受力出现偏差，导致贝雷无法达到等效预期效果。若实际使用过程中将贝雷支点设置在非竖杆处，必然会导致部分杆件内力偏大，而计算过程仍然按照梁单元等效简化，实际与理论不符。如图2所示，左边非标准贝雷制作随意，右边贝雷支点设置在非节点非竖杆处。

图2 贝雷实际使用示例

2.2 桁架计算控制杆件轴力

表3 贝雷桁架单元杆件承力设计值

此方法的优点是，计算过程较为简便，能比较好地反映贝雷构件真实受力。

此方法的缺点主要有两点：

(1)单一轴力并不能完全反映贝雷杆件受力情况。按照现行的钢结构设计相关的标准和规范，贝雷按照桁架计算均达不到可以忽略节点刚性的条件，也就是说贝雷构件的弯矩不可忽略，特别是在侧向荷载作用下，贝雷构件内力弯矩占比较大。

(2)《装配钢桥手册》贝雷构件理论容许承载力的计算考虑了构件的轴稳定性的折减，但是其构件的轴压稳定性计算与现行规范不一致。

①手册[1]计算如下：

自由长度l0=0.9×99=89cm

回转半径ry=1.18cm

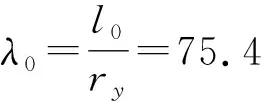
查表的轴心受压构件的稳定系数φ=0.66

②按《钢标》计算：

计算长度取桁架杆件节间长度l0=99cm

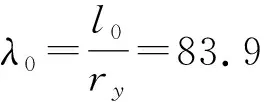
查表的轴心受压构件的稳定系数φ=0.544

可见二者相差1.2倍，对贝雷杆件的设计影响较大。

2.3 桁架计算控制杆件强度和压弯稳定性

本文定义为方法三，设计方法采用极限状态法，按照桁架对贝雷进行设计计算，控制贝雷杆件强度和稳定性，计算贝雷杆件的内力时荷载组合按照现行规范取分项系数。计算得杆件轴力和弯矩，然后按照相应的钢结构设计规范和标准进行杆件强度和稳定性验算。

此方法的优点是，完全依照现行的规范进行设计计算，可以真实地反映杆件受力情况，同时保证了杆件强度和压弯稳定性。

3 常见设计计算方法试验对比

为更加具象三种计算方法对设计结果的差别，笔者将进行一系列试验。主要试验方法为，针对同一结构和同一荷载，分别通过三种方法进行计算并进行比较。

3.1 方法一试验计算

工程实践中，普通321型贝雷的跨度一般在6～21m之间居多。本试验将选取单跨简支结构进行试算，试验跨度设计在6～21m之间，荷载为使贝雷达到其容许的弯矩或剪力所需的荷载，荷载定义为恒载，容许应力法荷载不乘分项系数，不考虑贝雷自重。结果如表4所示。

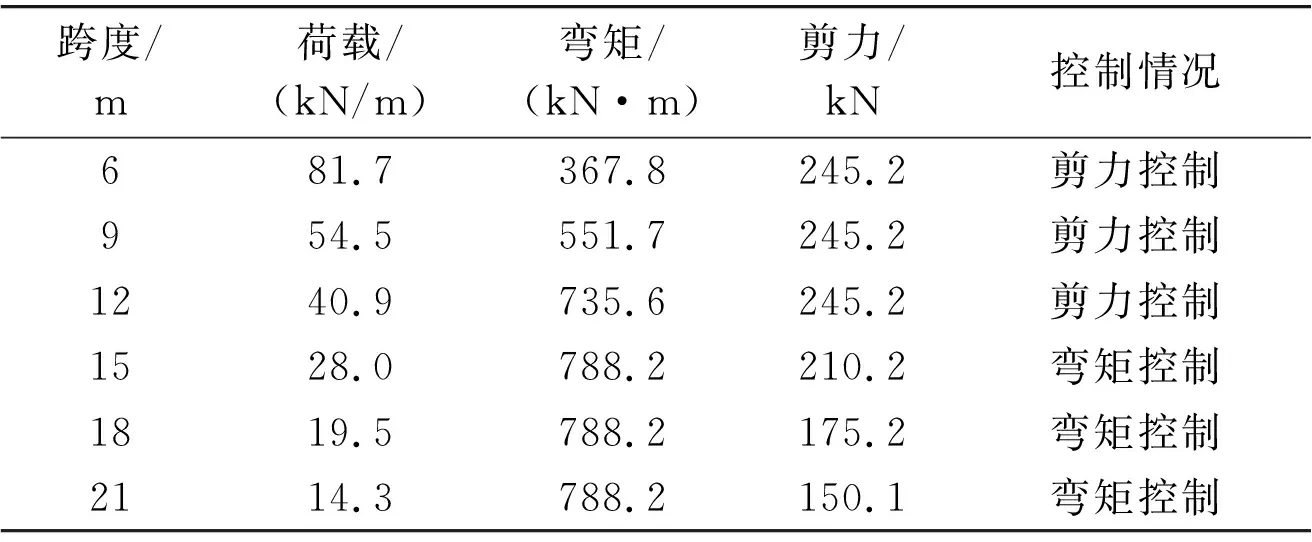
表4 方法一试验计算结果

3.2 方法二试验计算

试验对象为试验一中的跨度和荷载，按照《钢结构设计标准》(GB 50017—2017)进行计算，恒载分项系数取1.35。计算提取各杆件的轴力，整理如表5所示。

表5 方法二试验计算结果

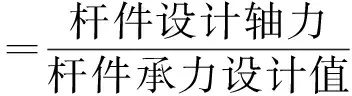
将方法二试验计算结果与方法一试验计算结果对比可知，按方法一计算满足要求时，贝雷在现行的规范体系内存在一定的安全风险。

二者差异主要原因有：2.2节中杆件承力提高比例系数1.117与荷载分项系数1.35存在着不对等情况；荷载施加方式不同，《装配钢桥手册》荷载均以节点荷载施加，但是工程实际存在很多均布荷载的情况。

3.3 方法三试验计算

试验对象为试验一中的跨度和荷载，按照《钢标》进行计算，恒载分项系数取1.35。计算提取各杆件的轴力和弯矩，分别计算杆件强度和压弯稳定性，整理结果如表6所示。根据计算分析可知，贝雷各构件均为平面外稳定性控制设计，故表6只列出平面外稳定计算结果。

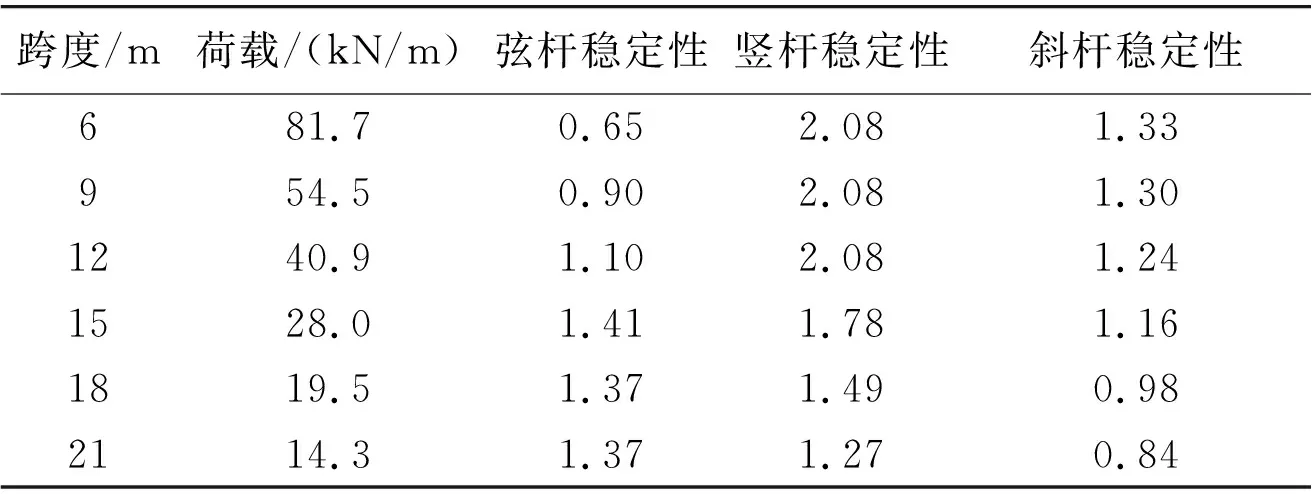
表6 方法三试验计算结果

从结果可知，方法三计算结果最不利。

方法三与方法二结果差异主要原因有：轴心受压构件的稳定系数计算存在差异；计算稳定性时弯矩是否考虑了弯矩的影响。

4 常见设计计算方法实例对比

4.1 工程背景

汉江孤山航电枢纽主体二标二期工程，左区泄水闸共7跨9个排架柱，两个排架柱之间设置系梁，系梁跨度17.8m，梁高1.5m，梁宽1m。系梁浇筑时采用贝雷梁结构，支架结构图如图3所示。

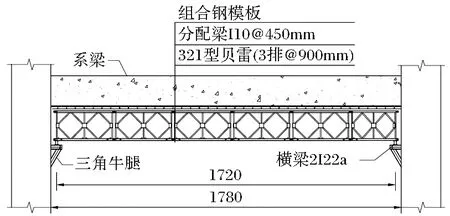
图3 系梁支架结构图

4.2 计算方法

对系梁支架分别按照3种方法进行建模计算，方法一贝雷按照梁简化建模，方法二和方法三贝雷按照桁架建模。

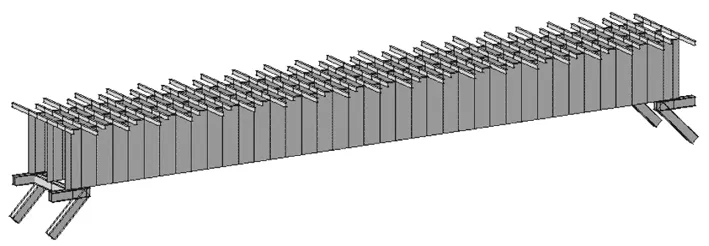
图4 贝雷按梁简化计算模型图

图5 贝雷按桁架简化计算模型图

4.3 计算结果对比

方法一计算结果：贝雷最大弯矩为678kN·m，最大剪力为169kN，满足要求，计算通过。

方法二计算结果：弦杆最大轴力为632kN，不满足要求，其他杆件均能满足要求。综合结果计算不通过。

方法三计算结果：弦杆最大应力为408MPa，不满足要求，上弦杆满铺分配梁，下弦杆受压，不计算弦杆稳定性；竖杆最大应力为268MPa，稳定性1.62，不满足要求；斜杆最大应力为223MPa，稳定性1.34。综合结果计算不通过。

从实例计算结果对比分析可知，在方法一计算通过的情况下，方法二计算不通过，方法三计算不通过。其中方法三计算结果更加不利，总体而言使用方法一的风险更大，方法二风险稍小，计算结果总体趋势与试验对比比较吻合。

5 结论及建议

从上述试验对比分析和实例对比分析可知，在现行规范体系下，方法三更加适用于贝雷结构的计算。方法三的计算方法既能模拟贝雷的真实受力，又能很好地契合现行规范，安全可靠。