BFe10-1-1 合金变形抗力的研究

付利国，郭 悦，马 宁，郭 桦，吕光辉，陶 欢，郁 炎

（中国船舶集团有限公司第七二五研究所，河南 洛阳 471023）

BFe10-1-1 合金是以镍、铁、锰为主要添加元素的铜合金[1]，具有优良的耐海水腐蚀性能和抗海生物污损性能，长期以来铜镍合金以其优异的可加工性，耐腐蚀性以及抗海生物附着等优点在海洋工程、船舶系统等领域中有着重要的应用[2-4]。在实际应用中，BFe10-1-1 合金主要是以管材及管系附件（如凸缘、法兰等）的形式应用，而其形成方式需要经过高温塑性加工成形[5-6]。变形抗力是表征合金塑性加工性能的一个基本参量，是材料成形过程中变形和受理计算的基础。金属的变形抗力值对于计算各种压力加工的力和功，制定工艺规程，设计、校核压力加工设备和工具都是必不可少的。正确揭示热变形过程中组织和性能的变化以及塑性变形的机理及其规律，对于建立合理的变形抗力数学模型，提高计算机在线控制能力，改善产品质量，具有重要作用[7-8]。

本文以BFe10-1-1 合金为研究对象，利用Gleeble-3500 对其进行热模拟圆柱压缩试验，分析BFe10-1-1 合金塑性加工过程中变形温度、变形程度、变形速率等参数对该合金变形抗力的影响，建立其塑性变形抗力模型，旨在为该合金的热加工工艺制定和有限元模拟提供理论和数据支持。

1 实验材料与方法

1.1 实验材料

实验材料为半连续铸造方法制备的BFe10-1-1合金铸锭，其化学成分如表1 所示。图1a 为实验合金铸锭原始组织，可以看出，主要由树枝状单相α 组织组成。为了便于塑性变形，防止开裂，实验前须对铸锭进行均匀化退火，以使晶内偏析扩散均匀。均匀化退火后铸锭的组织见图1b，可以看出为近似的等轴状晶。经均匀化处理后的铸锭采用线切割加工成尺寸为ø10mm×15mm 的圆柱试样，两端开槽，槽宽s=0.4mm，深t=0.2mm。

图1 实验合金均匀化前后的金相组织

表1 实验用BFe10-1-1 合金的化学成分/（质量分数%）

1.2 实验方法

实验在Gleeble-3500 热模拟试验机上进行，实验过程如图2 所示。将试样以10℃/s 的升温速度升至变形温度T 后，保温3min，以消除温度梯度，然后开始压缩变形。合金的变形温度T 分别为800、850、900、950、1000℃，应变速率 分别为0.01、0.1、1、10、15s-1，变形量均为60%。

图2 合金热压缩过程示意图

热压缩试验过程中，试样两端的凹槽内填充专用润滑剂（75%石墨+20%机油+5%硝酸三甲苯脂），以减少试样与试验机压头之间的摩擦，使试样在热压缩过程中变形均匀。

2 结果与分析

2.1 变形温度对变形抗力的影响

变形温度对变形抗力的影响如图3 所示。由图可知，在变形程度一定时，实验合金的变形抗力随着变形温度的升高而降低，在变形程度和变形温度一定的情况下，变形速率越大，变形抗力也随之增大。在变形温度和变形速率一定的条件，随着变形程度的增加，实验合金的变形抗力也相应增加。这是因为温度对变形抗力的影响主要表现在以下两个方面：首先随着变形温度的升高，发生的回复软化作用越来越强，位错在变形过程中通过交滑移和攀移等方式运动，在位错积聚区会发生部分位错的重新排列，有利于降低由于位错应力场引起的畸变能；其次，在畸变能的积聚区会发生动态再结晶现象，较低温度的大变形量会诱发大量的动态再结晶，使动态再结晶成为主要的软化方式，随着变形温度的升高，畸变能不易累积，动态再结晶难以发生，只有在足够的变形速率下才能发生动态再结晶的软化作用。

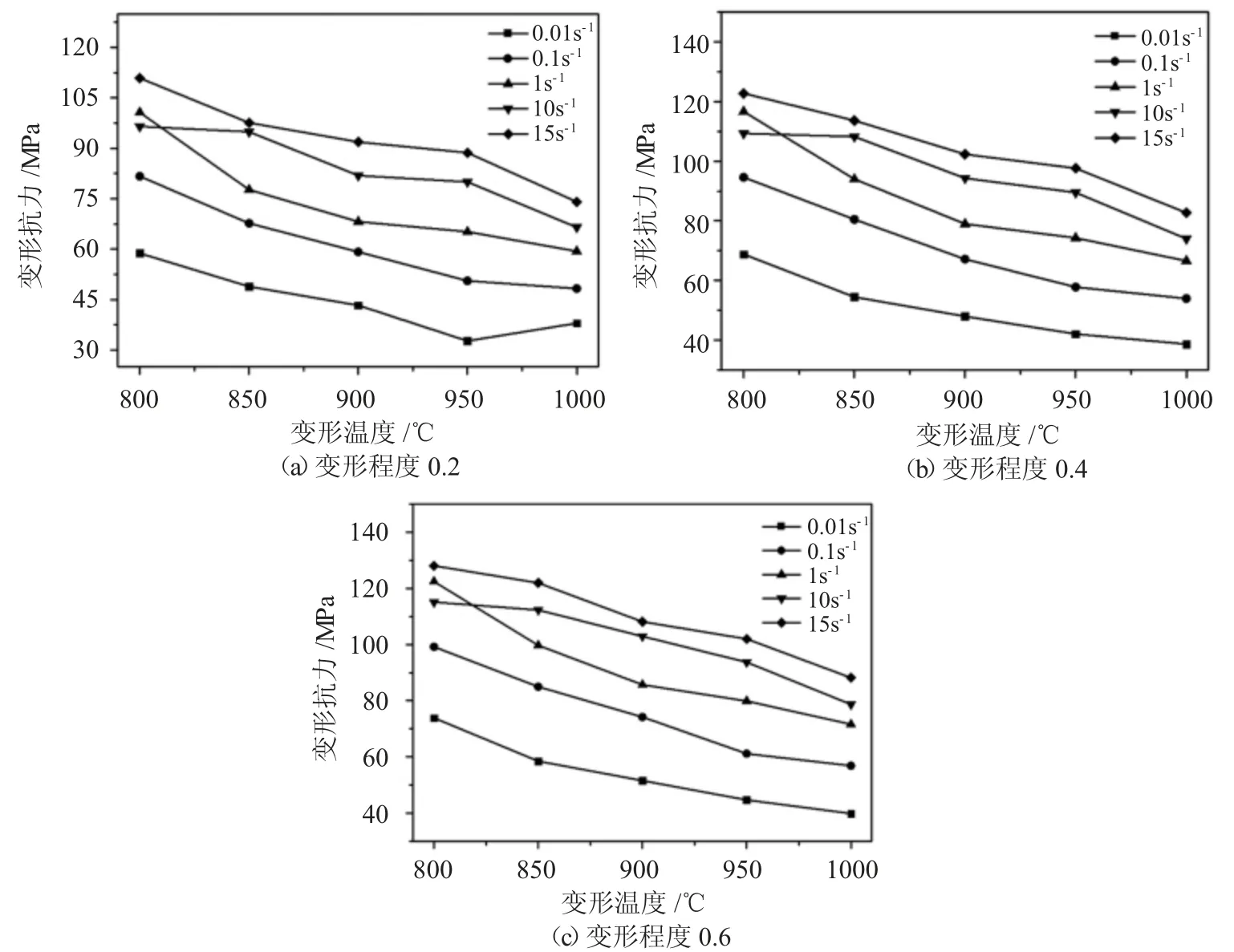
图3 变形温度对变形抗力的影响

2.2 变形程度对变形抗力的影响

图4 为变形程度与变形抗力的关系曲线。由图可知，变形抗力均随着变形程度的增加而增大。在变形程度一定时，随着变形温度的升高，变形抗力降低。当变形温度较低时，变形抗力随着变形程度的增加有比较明显的增加；变形温度较高时，变形抗力随变形程度的增加变化趋势减缓。变形速率增加时，同一变形温度和程度的变形抗力也增大。这是因为在变形程度一定时，在较低变形温度、较高变形速率的条件下，动态再结晶需要的驱动能增加，金属在高温塑性变形过程中来不及发生回复和再结晶，硬化作用大于软化作用，变形抗力增加。在变形速率一定时，在较高的变形温度条件下，随着变形程度的增加，金属发生了动态回复和再结晶，抵消了加工硬化，随着变形量的增加，位错密度增大引起的变形抗力与动态回复和再结晶处于平衡状态，所以曲线变缓。

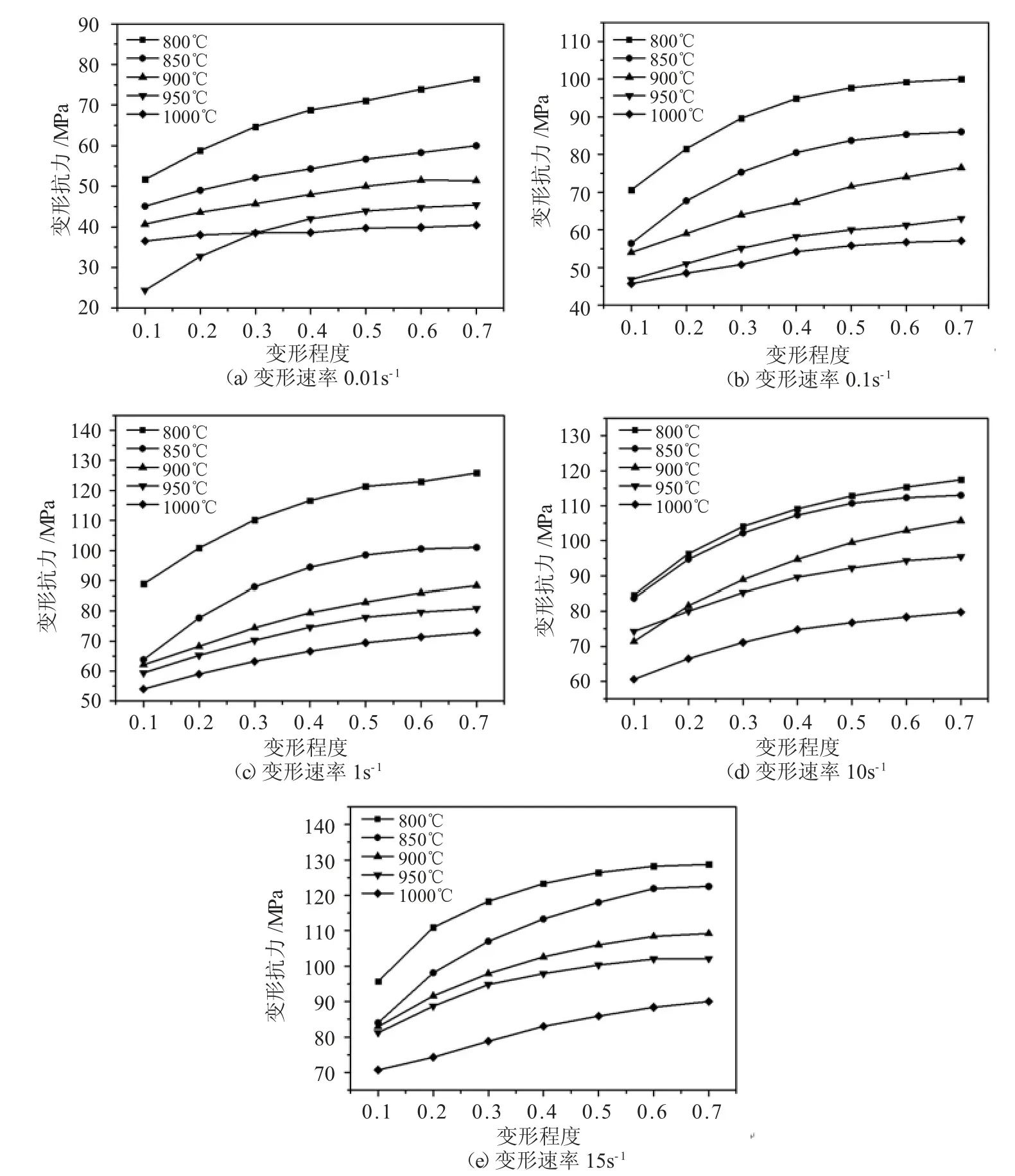
图4 变形程度对变形抗力的影响

2.3 变形速率对变形抗力的影响

图5 为变形速率与变形抗力的关系曲线。由图可知，当变形速率小于2s-1时，随着变形速率的增加，变形抗力有比较明显的增加；当变形速率在3～15 s-1之间时，随着变形速率的增加，金属变形抗力的增加比较缓慢。这是因为当应变速率较低时，金属的加工硬化起着主导作用，且由于应变速率较低，无法积累足够的畸变能，硬化作用远远大于回复和再结晶的软化作用，因此变形抗力增加较快。当应变速率增加到3s-1以后，尽管金属的加工硬化持续增加，但由于变形较快，金属中的畸变能得以快速积累，畸变能达到一定程度后，动态回复与再结晶软化作用于加工硬化作用达到动态平衡后，变形抗力曲线便进入稳定阶段。动态再结晶属于不完全软化，但软化率较高，随着应变速率的增加再结晶软化率降低，变形抗力缓慢增加。

图5 变形速率对变形抗力的影响

2.4 变形抗力数学模型

金属变形抗力的大小，决定于金属的组织成分、变形温度、变形速率、变形程度以及加工过程中的加工硬化、动态回复和再结晶。这些因素共同影响着金属的变形抗力。冷加工过程中，由于扩散作用被抑制，金属的变形抗力被加工硬化所主导，软化因素只有少量的位错回复、交滑移等不完全软化方式。热加工过程中，包括各种回复以及再结晶的发生，其中静态再结晶属于完全软化因素，动态再结晶属于不完全软化，但软化作用明显，这些因素在热加工过程中对变形抗力的影响巨大，不能像冷加工过程忽略。因此，热加工过程的变形抗力数学模型可用公式（1）表达[9]：

金属中的合金元素对金属变形抗力的影响相当复杂，不仅要考虑各个元素被添加进金属中的影响，还需要考虑各元素间的交互作用。此外，金属的应力状态、各部分变形程度不同等也会导致金属各部分表现出不同的变形抗力，因此很难实现把各种合金都放到一个变形抗力模型中，通常按不同的合金建立各合金的变形抗力模型，这种方法可以得到简化的变形抗力模型。

以金属的变形条件、组织状态及化学成分在某一特定条件下得到的变形抗力为基值，用σ0表示，对应的变形温度、变形程度、变形速率分别用t、ε、表示，则公式（1）可简化为：

在建立变形抗力模型时，有将变形温度、变形程度、变形速率视为独立变量互不影响，也有认为三者之间互相影响加以考虑，本文选用的模型考虑了t、ε、之间的相互影响，可由公式（3）表示[10]：

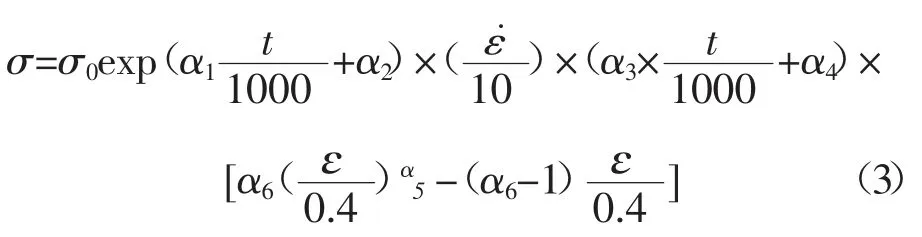
将实验各变形温度、变形速率和变形量下的变形抗力进行非线性回归，计算各回归系数值，表2 为变形温度950℃、变形量0.4、变形速率1s-1变形抗力模型回归系数。

表2 变形抗力回归系数分析结果

从表2 中可知，公式计算值与实测值的平均相对误差为4.21%，相关系数R 为0.9853，表明回归方程具有较好的曲线拟合特性。

3 结论

（1）在一定变形温度和变形程度下，变形抗力随变形速率的增加而增加。在一定变形速率和变形程度下，变形抗力随着变形温度的增加而减小。在较小的变形温度和较高变形速率下，变形抗力增加显著。

（2）在考虑变形温度、变形速率、变形程度对变形抗力交互影响下，建立了实验合金变形抗力数学模型，由实验数据通过回归分析得到的变形抗力数学模型有较高的预测精度。