基于重复脉冲法的发电电动机转子匝间短路诊断实践

张 利，孙士涛，王晓军，张 婷，邵卫超，张 杰，雷 雨，刘柏延

（1.国网新源控股有限公司北京十三陵蓄能电厂，北京市 100037；2.华北电力科学研究院有限责任公司，北京市 100045）

0 引言

抽水蓄能电站在电网中承担着峰谷调节的重要作用，发电电动机目前广泛应用于抽水蓄能机组。发电电动机的转子为显极式的磁极结构，绕组匝数较多，匝间绝缘多为很薄的绝缘垫片，由于机组启停频繁、采用空气间接冷却、运行中巨大的离心力等因素，匝间短路故障发生频次较高。虽然轻微的转子匝间短路并不意味着机组无法运行，但如果继续发展会导致转子振动增大、无功降低，甚至会引发转子接地导致停机[1]。

目前，在水轮机转子匝间短路的诊断上，有采用磁通探测线圈[2]的在线监测方法，但该方法的诊断灵敏度容易受到机组有功、无功负荷的影响，并不能完全替代离线试验手段，而目前主要的离线诊断手段是磁极的交流阻抗测试[3]，但该试验一般只能在机组拆除机盖或吊出转子后进行，不能做到随停随检，在机坑内进行还会受到定子磁路的影响，诊断灵敏度比较低。近年来，重复脉冲法（以下简称RSO法）[4]在汽轮发电机等隐极式转子上应用较为广泛，诊断效果明显，已经列入相关的电力行业标准[5]。由于RSO法属于一种转子绕组整体进行而非单个磁极分别进行测试的方法，若其能够应用至发电电动机，那么，结合抽水蓄能机组启停灵活的特点和该方法测试快速简捷的优势，可以根据需要做到转子匝间短路的随停随检，及时发现缺陷并进行处理，具有十分广阔的应用前景。但显极式转子与隐极式转子在结构上差别较大，RSO法在抽水蓄能发电电动机上的应用甚少，其适用性以及诊断效果尚缺少深入的研究。

本文尝试采用RSO法进行发电电动机转子匝间短路诊断，通过实验平台的搭建和真实机组上的测试，对该方法的适用性和关键因素进行了研究。

1 RSO法

RSO法属于一种时域脉冲反射方法，如图1所示，其基本原理是将一对完全一致的具有快速上升边沿的脉冲电压注入转子绕组两极和地（轴）之间，通过对比两极的响应波形来判断转子有无匝间短路。如果转子绕组没有匝间短路，由于正负极绕组的高度对称性，两极电压响应是完全相同的。如果存在匝间短路，破坏了两极绕组的阻抗对称性，则两极电压响应会出现差异。对于应用较多的隐极同步发电机转子，重复脉冲的形式有双指数波、方波等形式，激励脉冲顶值一般在10V左右。

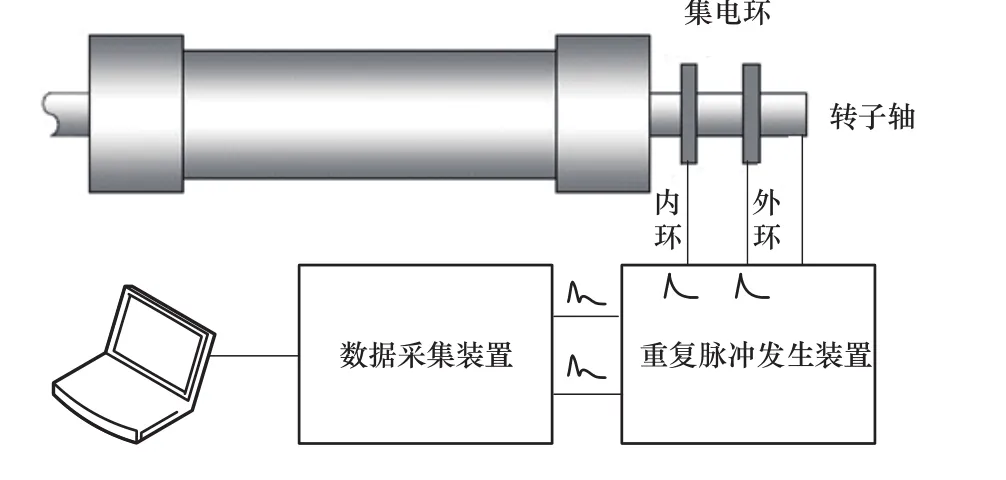
图1 RSO法测试示意图Figure 1 Test sketch map of RSO

发电电动机转子绕组虽然由多个分立的磁极组成，但各个磁极从结构和参数上都是高度一致的[6]，因此，从转子绕组首末两端看，无论其极数是多少，其也应是高度对称的。因此，从原理上来说，重复脉冲法对于发电电动机也同样适用。但是，由于显极式转子的极数、绕组匝数更多，绕组的长度更长，RSO法的脉冲形式和参数需要进一步考虑。

2 实验平台

基于重复脉冲法的基本原理，本文采用方波重复脉冲，搭建通用的实验平台，并结合发电电动机转子绕组特点确定平台参数。该平台由信号发生装置、功率放大装置、可调电阻、采集装置组成。

信号发生装置采用通用的信号发生器，能够输出标准方波脉冲，要求具备两通道输出同相位功能，保证两路输出尽量在同一时刻触发，这是重复脉冲法的基本要求。另外，方波脉宽、占空比、幅值、直流偏置应可调，保证脉冲的激励与负载相匹配。

发电电动机转子的结构和尺寸对重复脉冲的能量提出更高的要求，信号发生器产生的方波幅值有限，一般最大为±5V，且带载能力有限，因此需要采用功率放大装置对其进行放大。功放要求为两路，且应满足以下要求：

（1）可调而且足够大的增益，以便研究不同脉冲幅值下的故障诊断效果。

（2）足够的带宽，防止对高频上升沿的大幅衰减，导致功放次级输出激励信号的带宽下降，影响诊断效果。

（3）足够的容量，因为激励脉冲幅值越高，负载脉冲电流有效值也越高。

（4）功放输入阻抗要与信号发生器输出阻抗相匹配，否则会导致输出电压产生误差。

功率放大器对信号发生器的输入信号放大后，对外是一种低阻输出，目的是提高负载电压，因此，需要可调电阻实现测试系统内阻与绕组负载阻抗的匹配，最大限度地增强故障信号。本文选取0～2kΩ可调电阻。

采集装置采用具备20M/S的采样率和16位的采集精度的录波仪，保证微小的故障差值能够有效识别，减小采样的背景噪声。另外，采样装置的量程要满足高幅值电压的测量需要，并具备合理的自动触发模式。由于重复脉冲法的原理为两路信号作差，采集装置最好还要具备通道作差功能，以便直观地观察故障特征。

本文搭建的试验平台如图2所示。

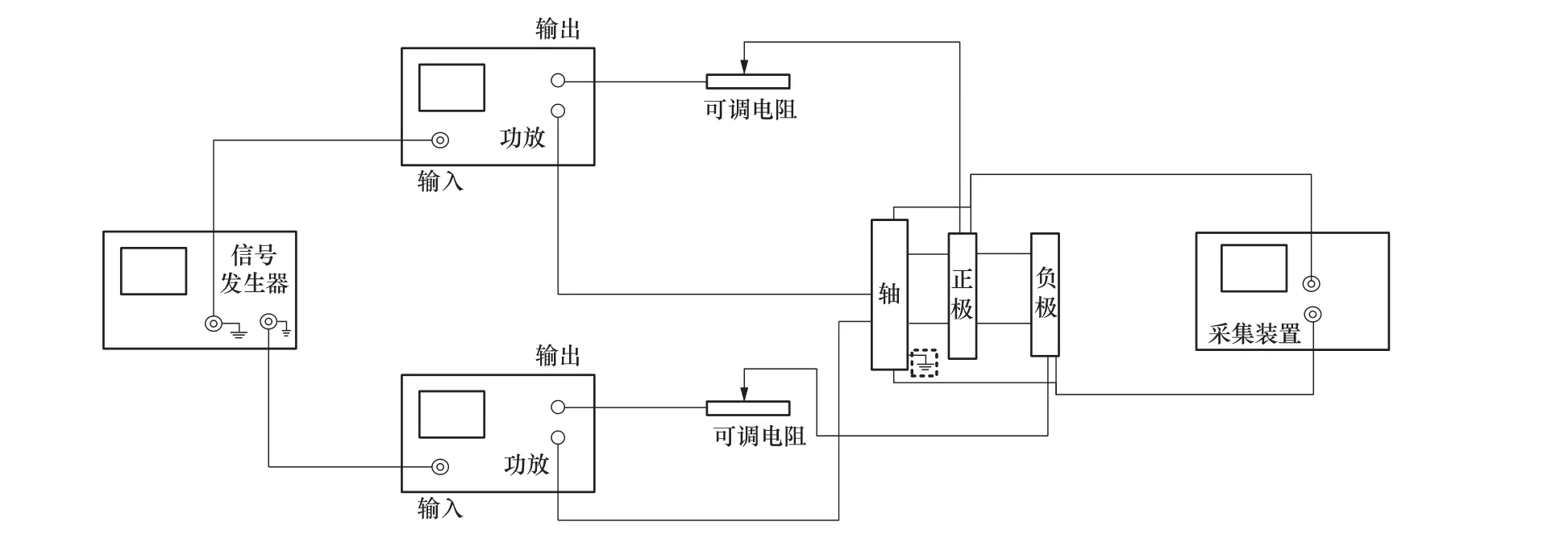
图2 平台组成与接线Figure 2 Platform’s composition and wiring

3 现场测试与分析

本文利用上述试验平台在北京十三陵抽水蓄能电厂2号发电电动机转子上进行测试。该机组容量为200MW，转子有12个磁极，每个磁极有29匝线圈。由于该转子磁极为返厂后的新磁极，因此，其本身的绝缘状态是良好的，不存在任何形式的匝间短路或接地，通过在绕组上人为模拟各种类型和位置的匝间短路故障点，可以得到比较细致的真实故障数据。

3.1 绕组中波的传播特性测试

在转子绕组末端开路时，首端施加1kHz，占空比50%，0～8V的低幅值方波信号（无需功放放大），首端内阻R=0，转子首末两端的电压波形如图3所示，其中，ChC1为首端电压波形，ChC2为末端电压波形，纵坐标为电压，横坐标为时间（图4～图8图示与此相同）。可见，负载波形直接阶跃至8V，且上升沿出现振荡，说明内阻的存在是必需的，内阻为零会导致负载分压直接等于空载输出电压，将观察不到故障点导致的负载分压的差异。另外，末端波形与首端波形起始处相比存在一定延时，可以认为是方波脉冲在绕组中传播的时间。

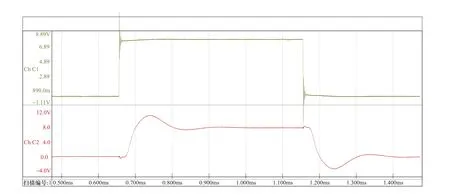
图3 末端开路，R=0时的测试波形Figure 3 Test waveform at R=0Ω with open end

末端开路，调节首端R=1270Ω，此时内阻过大，负载分压很小，半周期内脉冲难以达到稳态又进入下一个半周期，如图4所示，说明内阻过大会导致负载分压及暂态过程延长，同样会影响故障诊断效果。

图4 末端开路，R=1270Ω时的测试波形Figure 4 Test waveform at R=1270Ω with open end

末端短路，首端R=200Ω时的波形如图5所示。此时首端能观察到明显的末端反射，该反射使得输入电压出现跌落，证明转子绕组对于具有高频分量的脉冲波呈现传输线特性[7]。

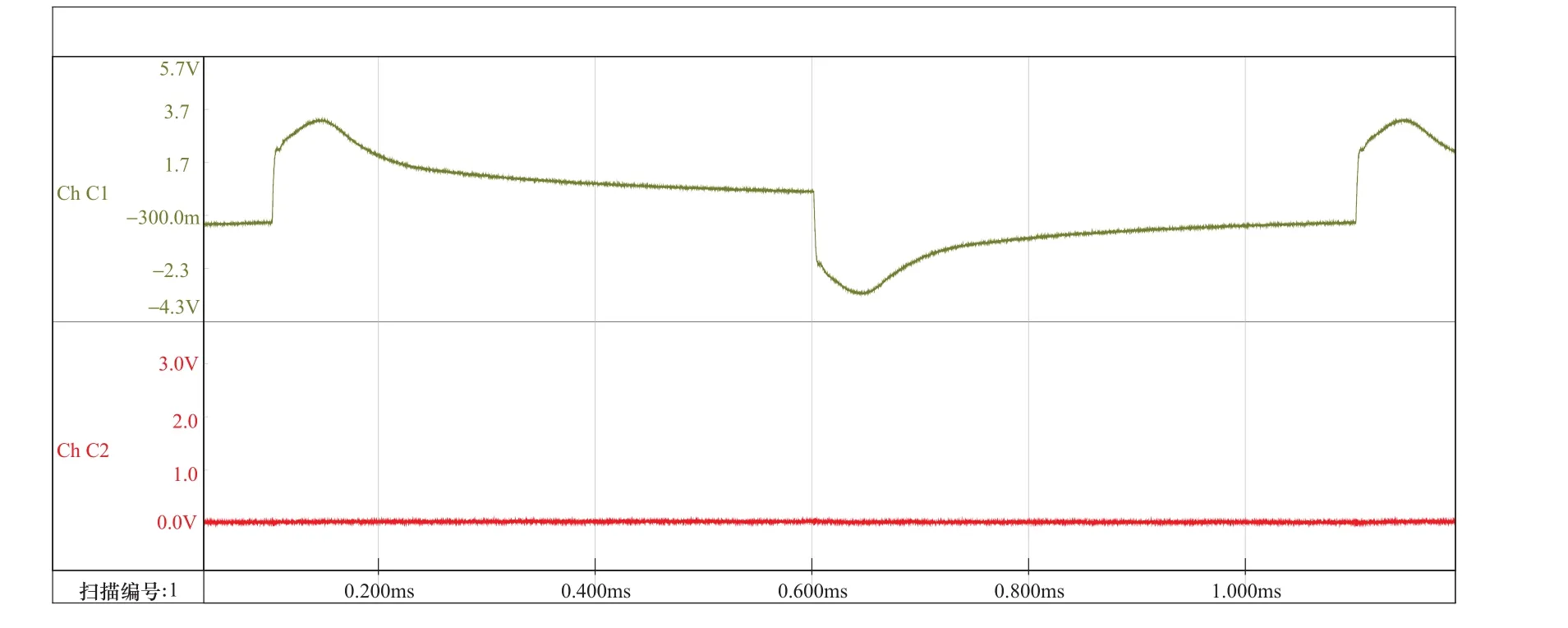
图5 末端短路，R=200Ω时的测试波形Figure 5 Test waveform at R=200Ω with short-circuit end

在末端并接电阻，调节末端电阻值，使得首端波形平滑上升至稳态直流值，此时末端反射回波效应基本消失，证明末端电阻与绕组阻抗达到匹配，得到匹配电阻约为475Ω，如图6所示。

图6 双端匹配后单端测试波形Figure 6 Single - end test waveform when double-end matched

3.2 故障模拟与RSO法测试

首先，调节两端内阻为匹配值，提高方波脉冲的幅值进行正常绕组的测试，得到绕组无故障状态下的典型RSO波形如图7所示，脉冲幅值为40V。可见，无故障状态且阻抗匹配时，绕组两端的负载电压波形基本重合，且上升边沿平稳过渡至直流稳态，无明显过冲或跌落等反射现象，符合前述匹配规律。

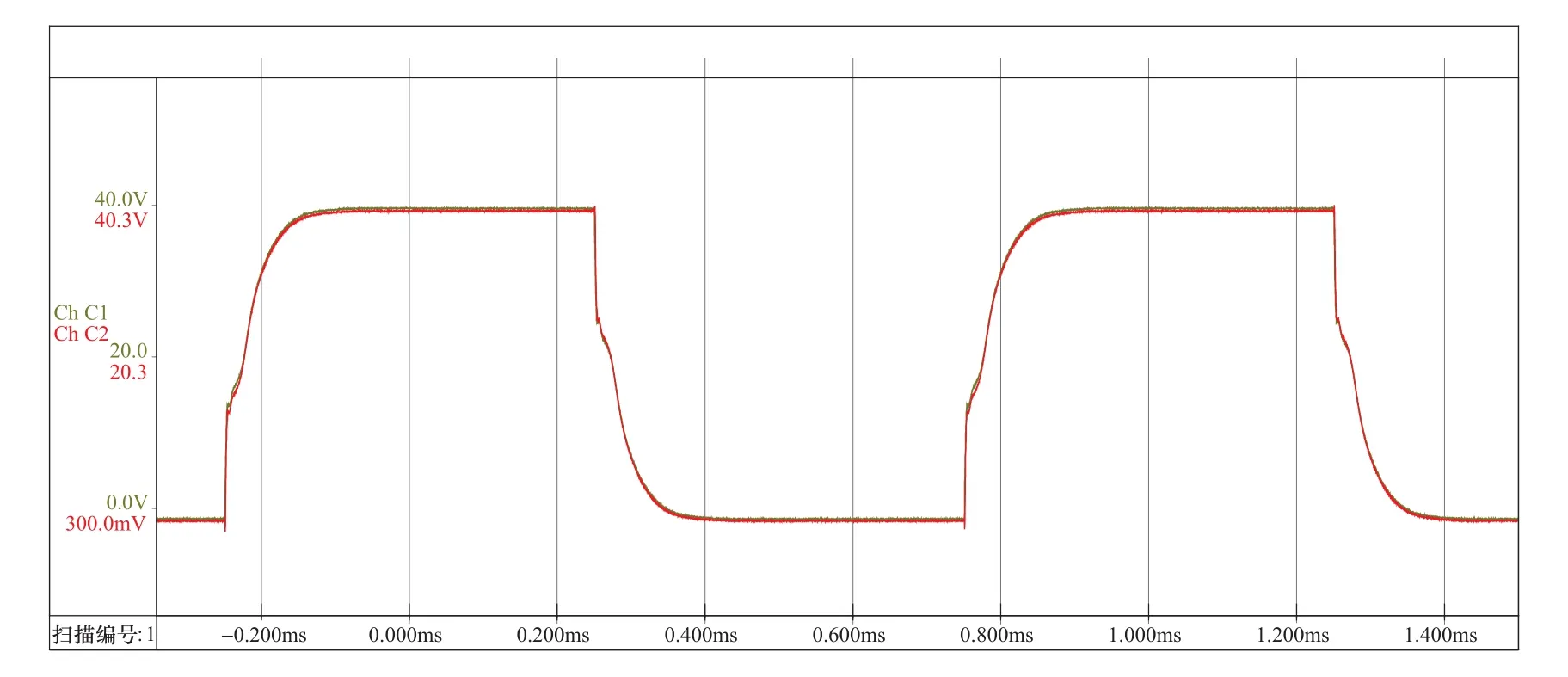
图7 双端匹配后正常绕组RSO测试波形Figure 7 RSO test waveform of normal winding when double-end matched

通过各磁极人为模拟匝间短路，得到了绕组匝间短路时的故障响应，其中典型故障波形如图8所示。此时整体波形还是符合匹配规律，但在负载波形的上升阶段，两端响应局部出现差异，不再重合，如图8中虚线圆形标记所示。

将各磁极末端匝（28匝与29匝）分别短路时测得的两端差值波形汇总在图9，波形0时刻对应于图8中方波脉冲起始时刻，各极故障时的差值峰值大小和出现时刻汇总在表1。

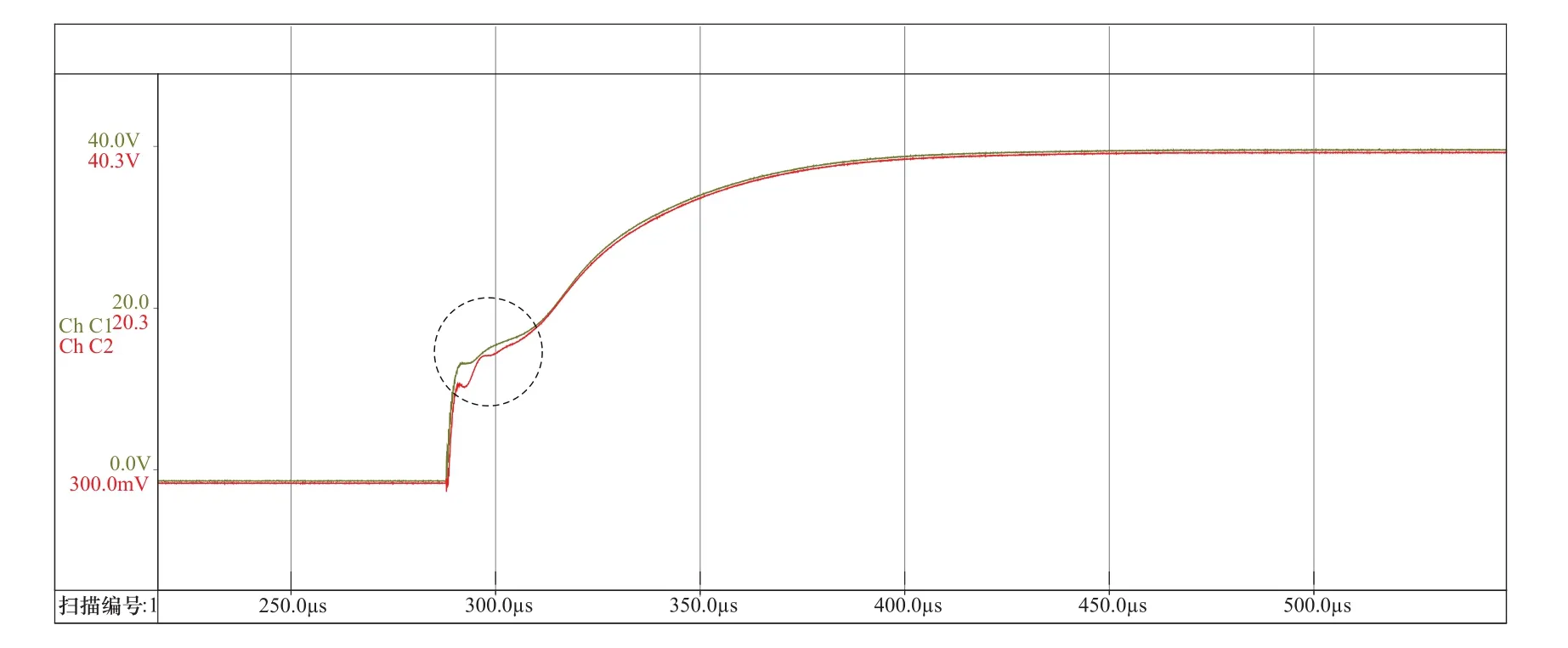
图8 典型故障波形Figure 8 Typical fault waveform

作为对比，信号发生器输出脉冲调整为±2.5V、±3V（未加偏置），不经功放放大，直接注入转子绕组两端，进行低幅值脉冲下的故障响应测试，结果如图10所示。由图10可知，采用5V峰峰值的方波激励时，第2极28匝发生匝间短路时，故障差值为0.13V，十分微弱，而采用6V峰峰值的方波激励时，第6极28匝发生匝间短路时，由于故障位置离测试端口更远，故障点引起的差值衰减严重，此时与正常绕组的响应波形一样已不存在明显的故障差值，说明采用低幅值的脉冲激励的诊断灵敏度较差，甚至无法有效检出远端故障。对比表1和图9，对于第2极28匝故障以及第6极28匝故障，提高脉冲幅值至40V后，故障特征差值提高至1.29V及0.4V，对于第6极故障，进一步提高脉冲幅值至73.5V，故障特征差值提高至0.59V。可见，提高激励脉冲幅值能够有效增强故障特征，增大故障诊断灵敏度，尤其是对于远端故障，可以诊断出低幅值下无法检出的故障。由于对12极的转子绕组，第6极28匝位于绕组中心，发生一匝的匝间短路时产生的故障特征是最微弱的，此时诊断灵敏度已经能够保证，对于其他位置和更多匝数的匝间短路同样能够诊断。

图9 各极故障差值Figure 9 Fault difference of each pole

图10 低幅值脉冲下的故障波形Figure 10 Fault waveform under low-amplitude pulse

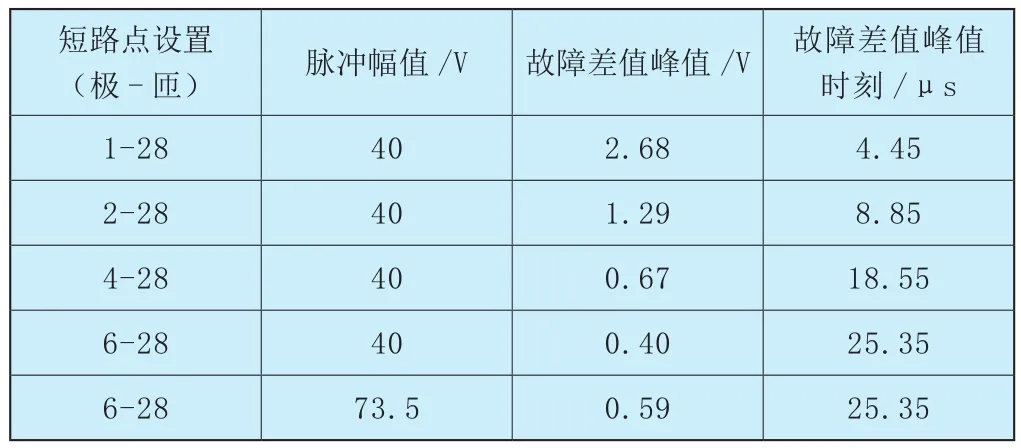
表1 不同磁极的故障特征数据Table 1 Fault characteristic data of different magnetic poles

从不同磁极位置的故障特征峰值时刻来看，随着故障点越来越远离测试端，故障峰值出现的时刻也越来越晚，基本成比例增加，说明注入脉冲在绕组中的传播速度近似为恒定值，因此，可以采用行波原理进行故障的初步定位[8]，如式（1）所示，其中tn可以根据图3中绕组首末端波形的延时得到，所谓近端指的是负载响应波形中出现差值的部分中电压较低的一端，如图8中ChC2端，这是由于故障点的反射信号会导致更近的一端电压波形率先出现跌落。

式中：Lf——故障点距近端端口的距离，m；

tf——故障差值峰值时刻，s；

tn——波在整个绕组中的传播时间，s；

Ln——绕组长度，m。

根据图9，不同磁极绕组发生匝间短路时，同样的故障程度下，故障差值的大小随故障点位置衰减非常明显，因此，不能用一个统一的故障差值判据来对相同的故障严重程度做出判定，诊断时可以结合故障点位置，分磁极设定故障诊断阈值。

4 结论

本文搭建了发电电动机转子匝间短路RSO法通用测试平台，并针对真实转子进行了现场实践，对重复脉冲在绕组中的传播特性、诊断效果及适用性等进行了分析，得出以下结论：

（1）在具有高频分量的脉冲激励下，发电电动机转子绕组呈现传输线特性，存在端口反射、阻抗匹配等特征。

（2）采用高幅值的激励脉冲能够明显提高RSO法的故障诊断灵敏度，增强波形的故障特征。

（3）RSO法通过选择合理的脉冲形式和参数保证诊断灵敏度后，可以应用于发电电动机等长绕组转子，与隐极发电机转子类似，以双端的故障响应差值为特征，可以对故障进行诊断和初步定位。

另外，在实际应用方面，高幅值的激励形式对成型测试设备的容量、测量系统提出了更高的要求，需要在脉冲产生形式、重合度保证、带载能力等方面做进一步的考虑。