基于聚类与Markov 链法的西安市某线路城市客车工况构建
2022-07-17李耀华邵攀登翟登旺任田园宋伟萍赵承辉
李耀华,邵攀登,翟登旺,任田园,宋伟萍,刘 洋,赵承辉
(长安大学 汽车学院,西安 710064,中国)
汽车行驶工况是基于汽车实际行驶数据,并结合相关数理统计方法来定量描述典型道路车辆行驶状况的速度—时间曲线。高精度的汽车行驶工况能够真实反映在实际行驶过程中车辆状态的变化规律和用户的使用需求,是汽车行业中的一项极其重要的共性技术[1-3]。中国幅员辽阔,地区差异较大,各个城市间的道路和交通状况和驾驶员驾驶习惯存在差异。刘希玲等曾对北京、天津、上海、大连和广州5 个城市的汽车行驶工况做了对比,结果表明各城市间的车辆行驶状况有很大差别。因此,针对特定区域构建符合当地车辆行驶特征的行驶工况就有着较大的意义[4]。
目前,工况构建方法大多基于短行程,采用V-A矩阵法、聚类分析法、Markov 链法等方法构建工况。S. K. Mayakuntla 等[5]提出了一种基于行程段的汽车行驶工况构建方法。王国林[6]等利用传统的短行程法构建了轻型乘用车的行驶工况。杜常清等[7]基于GPS/GIS 的短行程构建方法,将交通领域的大数据应用于城市工况构建中。N. H. Arun 等[8]基于全球定位系统(global positioning system, GPS)数据构建印度金奈地区乘用车和摩托车的行驶工况。G. Günther 等[9]利用短行程构建德国汉堡公交车行驶工况。李耀华等[10]基于主成分分析与聚类分析法构建了西安市电动客车行驶工况,并与其他典型城市工况进行了对比分析。C. Chandrashekar 等[11]探索了随机选择和k均值聚类2 种方法来构建工况。董恩源等[12-13]通过聚类分析法构建城市公交行驶工况。L. Berzi 等[14]扩充了部分运动学特征参数,构建意大利佛罗伦萨电动汽车的行驶工况。李耀华等[15-17]基于Markov 链法构建城市公交线路工况。P. G. Seers 等[18]考虑了郊区车辆和机场车辆的运行特殊性,构建有针对性的行驶工况。G.Amirjamshidi 等[19]利用多目标遗传算法校准仿真模型,基于仿真数据构建多伦多地区不同类型汽车的行驶工况。
本文结合聚类与Markov 链法构建了西安市某线路城市客车的行驶工况,确定了聚类个数及特征参数组合,提出了Markov 链法构建工况长度的确定方法,从能耗角度定义汽车行驶时的单位里程比能耗作为工况选取标准,从50 条候选工况中筛选出该线路的代表工况,并建立了基于Cruise 软件的纯电动客车整车模型,从数据结构和百千米能耗对比了聚类法工况、V-A矩阵法工况、基于聚类与马尔科夫结合法工况与样本数据的偏差情况。
1 数据采集及预处理
1.1 数据采集及片段划分
车辆实际运行数据是行驶工况构建的基础。本文采用车辆无线行驶记录仪对车辆行驶数据采集,将其固定安装在西安市某公交线路运营车辆上,从而实现对构建线路工况所需数据的不间断采集。本文选取了西安市某公交线路,该线路由西安市西南至东北,贯穿西安市一环至三环区域,涵盖了西安市主干道、次干道、城郊等典型的城市公交路线,线路路线长,运营强度大,具有较好的代表性。针对特定公交线路构建工况可为该线路公交车动力系统匹配选型和混合动力系统控制策略优化标定提供依据,实现精确的定制化服务和一线一标,为公交线路的运行能耗、排放及驾驶行为经济性评价提供依据,为特定公交线路运营提供数据服务,并可结合整车建模建立关键零部件的耐久性极限测试工况[20-22]。
本文以所选线路上的若干正常运营车辆作为试验车,进行了为期16 天的无间断数据采集,最终得到111组车辆从起点站到终点站的运行数据,并进行数据预处理,对不合理采样数据进行清洗。通过对采样数据分析,发现GPS 和尖点数据。怠速异常点表现为当车辆处于停止状态,由于GPS 存在扰动,采集数据有时并不为零,保持为一个较低数值。经分析,当车速处于4 km/h 以上时,车辆明显处于运行状态。车速数据处于4 km/h 以下时,速度处于0~1.5 km/h 的数据占比达到80%。因此,选取速度阈值为1.5 km/h。当车速低于1.5 km/h,则将其设定为零。从而保证怠速片段的精确性和完整性。车速离群点表现为车速明显高于序列一般水平。经调研,该线路主要在西安市内运行,拥堵严重,公交车运行车速一般低于40 km/h。因此,将高于40 km/h 的数据视为车速离群点。经统计,该类异常值所占比重极小,对数据完整性影响也极小,故采用直接删除处理方式。尖点数据表现为由于GPS 信号存在干扰,GPS 信号产生,使得加速度值出现过大的尖点。调研发现,该线路公交车实际运行的最大加速度与最大减速度分别为2.5、-3.5 m/s2,因此,将加速度超过限值的数据视为尖点,采用线性插值法处理。
研究表明:当样本数据达到饱和后,数据量的增加已很难提高工况精度,反而会增加后续的工作量[13]。本文选择加速比例、匀速比例、减速比例、怠速比例、平均车速和平均运行车速这6 个参数作为稳定性判定指标。定义其平均值随采样数据组增大的变化率为稳定度K,并将这6 个参数稳定度的平均值定义为综合稳定度,分别如式(1)和式(2)所示,其中和Ā6(j)分别为样本数据增加到j组时的加速比例、匀速比例、减速比例、怠速比例、平均车速及平均运行车速。

随着采样数据的增加,综合稳定度K的变化趋势如图1 所示。

图1 综合稳定度K 的变化趋势
由图1 可知,综合稳定度K随着数据量的增加逐渐收敛至0。从第41 次采样开始,连续5 次K的绝对值均小于0.002,且收敛速度开始变缓。因此,可认为样本数据在采样次数为45 时达到饱和。考虑到一定的裕度,本文取50 组采样数据作为构建工况的样本数据。
将车辆两个怠速点之间的运行片段定义为一个短行程,如图2 所示。通过对50 组数据的处理,本文最终得到2 830 个短行程。
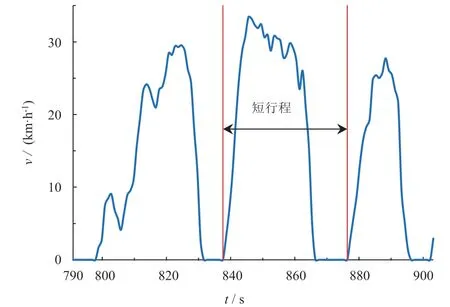
图2 短行程示意图
2.2 特征值组合及状态个数确定
运行片段可以由片段的特征参数描述。车辆工况构建一般采用平均速度(vmean)、平均加速度(amean)、平均减速度(Dmean)、平均运行速度(vmr)、运行时间(t)、速度标准差(vsd)、加速度标准差(asd)、最大速度(vmax)、最大加速度(amax)、最大减速度(Dmax);0~10 km/h 的时间比例为λ0-10、10~20 km/h 的时间比例为λ10-20,以此类推,20~30、30~40、40-50 km/h 的时间比例分别为λ20-30、λ30-40、λ40-50;加速时间比例(λa)、减速时间比例(λd)、匀速时间比例(λc)、怠速时间比例(λi)、加速时间(ta)、减速时间(td)、匀速时间(tc)、怠速时间(ti)、运行距离(Lr),共24 个特征参数。为了消除这些特征参数由于量纲和取值范围不同而引起的差异,本文对这24 个特征参数进行了z-score 标准化处理,如式(3)所示,
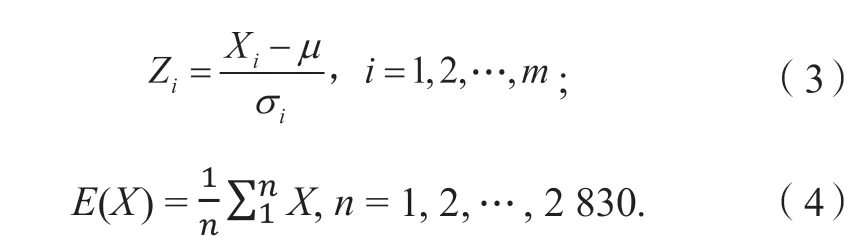
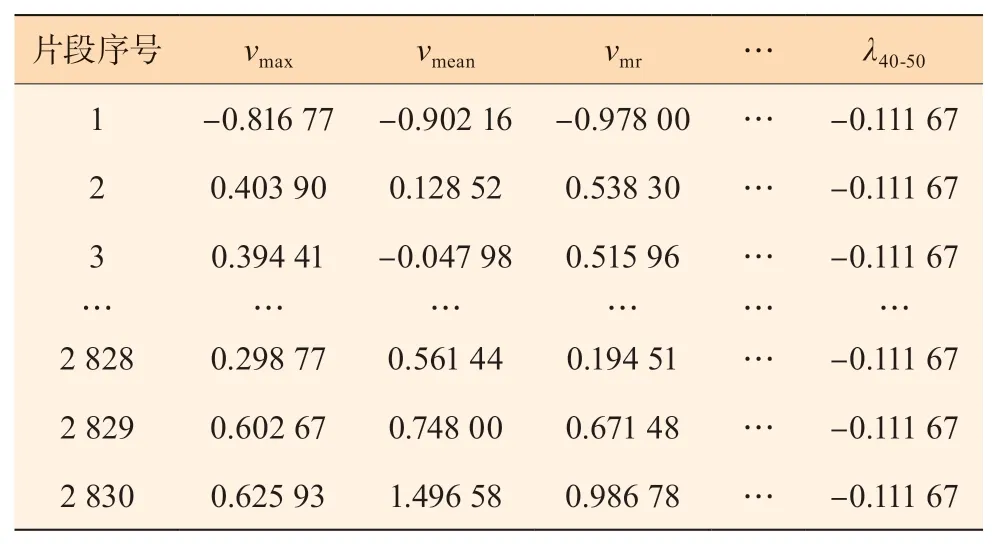
表1 特征参数标准化矩阵
聚类是构建工况中的关键一步。通过聚类可将数据片段合理的划分到不同的状态,然后根据各片段隶属状态的结果求取状态转移概率矩阵,最后在片段拼接时从所跳转的状态中挑选合适的片段进行工况长度的延伸。因此,聚类的结果好坏对工况构建的精度有较大的影响。
聚类试验结果表明,选取不同特征值组合与类的个数进行聚类,聚类的结果会有较大的差别[23-29]。为找出最佳特征值组合和类的个数,本文选取了30 组不同的特征值组合进行了类个数为3 个、4 个和5 个共90 次聚类交叉试验。90 次聚类试验的各类短行程个数分布如表2 所示。
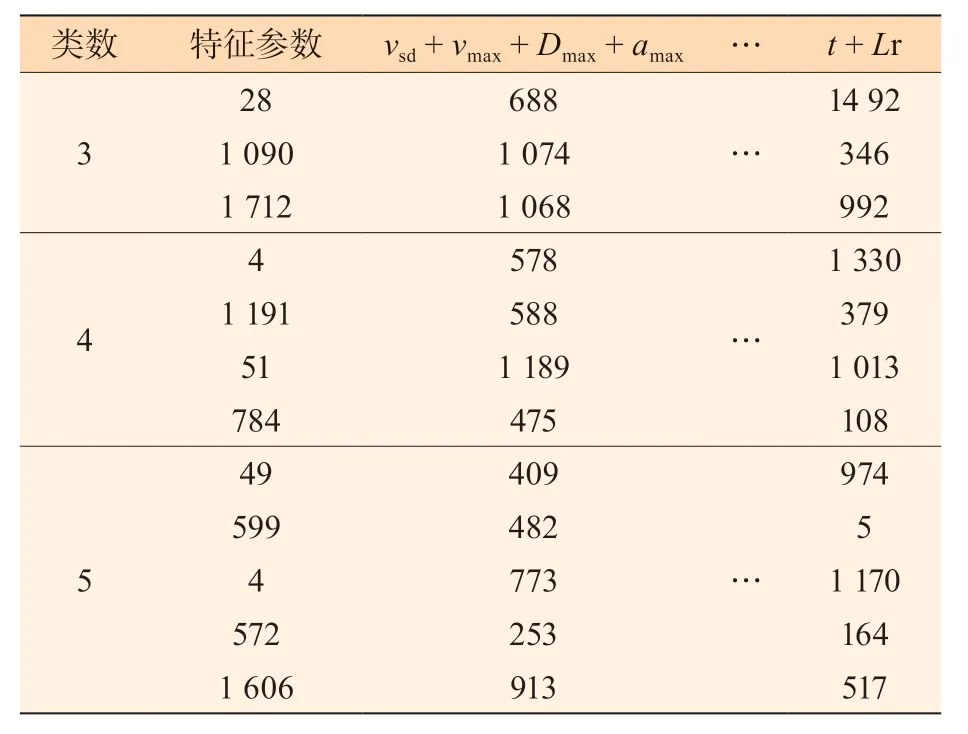
表2 不同类个数和不同特征参数组合的聚类分析结果
经过交叉试验可知,绝大多数情况下,选择的类的个数越多,聚类后在每一类中短行程个数的分布越不均衡,出现某一类中短行程个数过小情景的概率越大。对于本文的工况构建,聚类得到的结果即为Markov 链的状态空间。如果状态空间中某一状态的短行程个数过少,在进行状态跳转时,从上一时刻的状态跳转到该状态的概率几乎可以忽略不计,即使跳转到该状态,对最终构建出来工况的精度也有很大影响。因此,在选择状态空间时,应极力避免这种状况,结合表2,本文选择的聚类个数为3 个。此时,不同特征值组合聚类后得到的状态转移概率矩阵(P)如图3 所示。
车辆的行驶过程是一个连续且稳定的过程,发生状态跃迁的概率不大,反映到状态转移概率矩阵上即为对角线上的概率明显大于其他区域。聚类试验所得的结果中,图3d 所示的状态转移概率矩阵明显符合此特征。该特征值组合聚类所得样本数据的状态转移概率矩阵如式(4)所示。式(4)中对角线上数据最大,符合状态转移概率矩阵特征。
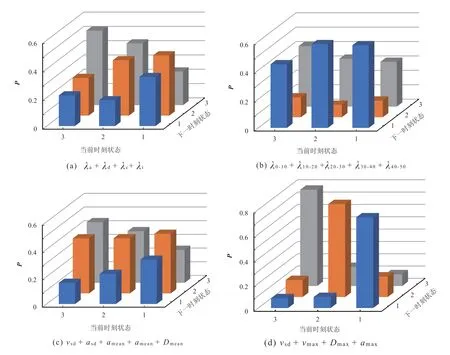
图3 不同特征值组合聚类后样本数据的状态转移概率矩阵

因此,本文选取的特征值组合为速度标准差vsd、最大速度(vmax)、最大加速度(amax)和最大减速度(Dmax)。
3 候选工况构建
在进行候选工况构建时应先选择合适的初始片段,判断初始片段的状态后结合状态转移概率矩阵进行状态跳转,而后从跳转的状态中选择拼接后与样本数据最相似的片段进行拼接。在多次的状态判定、状态跳转和片段选择的循环后,若拼接片段达到稳定即可结束工况构建,候选工况构建的主要流程如图4 所示。
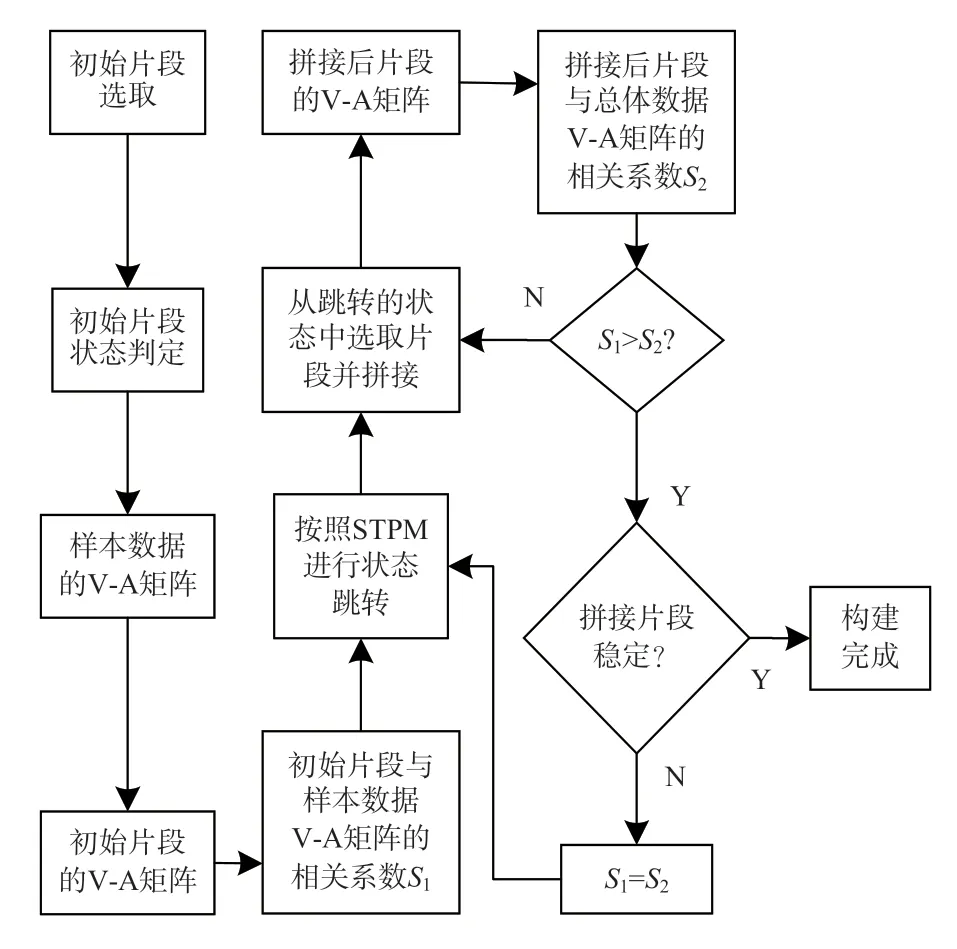
图4 候选工况构建流程
3.1 Markov 状态转移过程
Markov 过程是一个随机过程,记为Zt(t= 1, 2,…,T),状态空间记为S={1, 2, …,K}。Zt为每个状态t的模型事件,状态空间S是收集了相似模型事件编入事件组对的集合。对于t和所有的状态s1,s2, …,st,当前状态st的概率只与前一个状态st-1有关,对于一个Markov 过程,根据最大似然函数,其状态转移概率方程如式(5)所示。

其中:prs为状态转移概率,Nrs表示时间为(t-1)时状态r转移到时间为t时状态s的事件个数。
3.2 初始片段选取
初始片段的选取在Markov 法构建工况过程中对后续片段的拼接和最终结果的偏差有着至关重要的作用。本文将每个长行程的第1 个短行程(即公交车起点起步过程)作为候选工况的初始片段。图5 为某条候选工况初始片段。
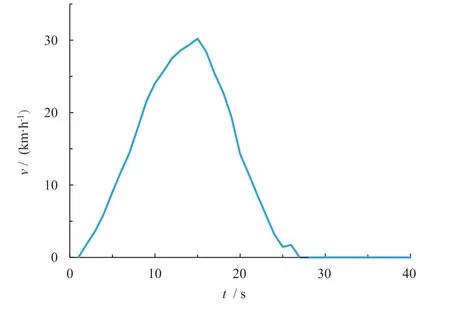
图5 某候选工况初始片段
3.3 工况构建
在工况构建时,每次状态跳转时都选择在不重复的情况下该片段在当前状态中拼接后与样本数据的V-A 矩阵相似度最高的片段进行拼接。判断片段与样本数据V-A 矩阵相似度的方法是先将2 个矩阵按同一种方式转化为一维数组,然后计算二者的Pearson 相关系数[r(x, y)]。Pearson 相关系数是将数据归一化后进行的余弦相似度计算,如式(6)所示,其中x和y为矩阵降维后的一维向量;为矩阵中所有元素的平均值;xi和yi为一维向量中的元素。该系数越接近于1,说明两个矩阵的相似度越高。
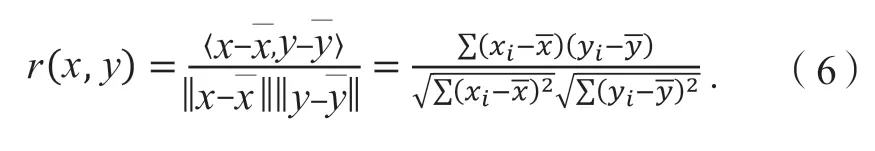
合理的工况长度对构建工况也很重要。工况长度如果过短,则无法反应城市客车的实际运行状况,但如果长度过长,则会无谓地增加工况构建及后期应用的工作量。本文将进行拼接后的片段与样本数据的V-A矩阵欧氏距离作为判断该矩阵是否稳定的标准,通过判断工况构建过程中的V-A 矩阵是否稳定来确定工况构建的长度是否合适。
V-A 矩阵的欧氏距离(D)计算式如式(7)所示,其中uij为样本数据V-A 矩阵元素;vij为拼接后片段V-A矩阵元素;m和n为V-A 矩阵行列数。
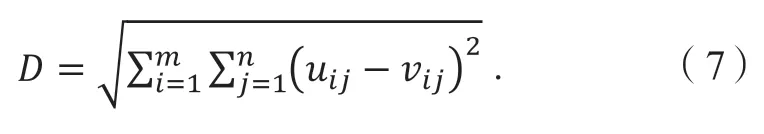
某工况构建过程中欧氏距离D值的变化如图6 所示。由图6 可知:该工况在拼接14 次(D= 0.033 919)之后曲线已经趋于稳定,此时再增加长度,对工况的精度提升不大,故该工况在拼接次数达到14 次时可跳出循环,结束工况构建。

图6 某工况构建过程中欧氏距离D 值的变化
4 代表工况选取
为了体现汽车行驶时的能耗状况,本文从能耗角度定义汽车行驶时的单位里程比能耗作为工况选取参考,如式(8)所示。

其中:Ws为车辆行驶过程中的单位里程比能耗[J/(kg·km)],γp为机动车比功率(kW/kg),L为车辆行驶里程(km)。根据比功率的定义,该采样车型γp计算公式如式(9)所示[30-32]。

其中:v为车速,a为车辆加速度。
单位里程比能耗直接反映了车辆行驶过程中克服阻力做功的大小,其值越大表明做功越多。经计算,50 条候选工况的单位里程比能耗计算如表3 所示。
经计算,样本数据的平均单位里程比能耗为168.04 J/(kg·km)。由表3 可知,第14 条候选工况与样本数据的单位里程比能耗相差最小,为168.06 J/(kg·km),相差0.02 J/(kg·km),偏差率最小,仅为0.012%。因此,本文将其作为西安市该线路城市客车的代表工况,如图7 所示,工况时长为1 419 s。

图7 西安市某线路城市客车行驶工况
该代表工况的部分特征值如表4 所示。
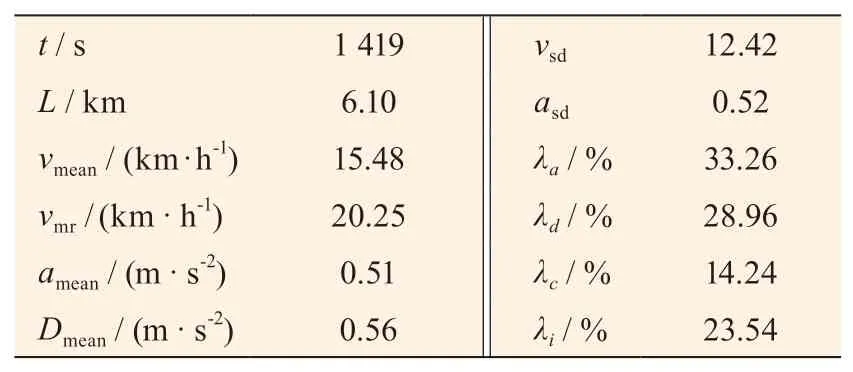
表4 西安市某线路城市客车行驶工况特征值
本文从数据结构相似度也对代表工况进行验证。样本数据和该代表工况的速度与加速度联合概率分布如图8 所示。图8 表明本文构建的工况与样本数据的速度与加速度联合概率分布基本一致。经计算,二者V-A 矩阵的欧氏距离仅为0.036 742,具有很高的相似度。
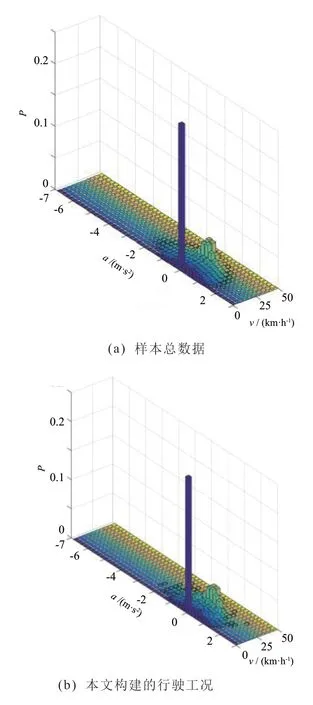
图8 速度与加速度联合概率分布图
同时,本文选取了平均速度(vmean)、平均加速度(amean)、平均减速度(Dmean)、平均运行速度(vmr)、速度标准差(vsd)、加速度标准差(asd)、加速时间比例(λa)、减速时间比例(λd)、匀速时间比例(λc)、怠速时间比例(λi)等10 个在工况构建中非常重要的统计量,分别计算了这50 条候选工况的10 个特征值,并将其分别与样本数据做了平均偏差检验。50 条候选工况与样本数据这10 个特征值的偏差率的平均值定义为平均偏差率,经计算结果如表5 所示。由表5 可知,本文构建的行驶工况与样本数据偏差较小,平均偏差率为1.17%。在数据结构上与样本数据相似度较高。
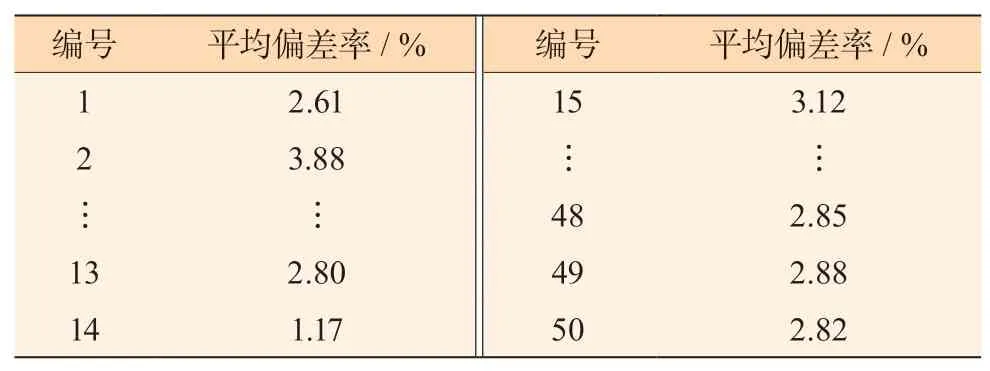
表5 50 条候选工况与样本总数据平均偏差率
5 仿真验证
为了验证基于聚类与Markov 结合法构建工况的精度,基于相同的样本数据,本文分别使用聚类法和V-A 矩阵法构建了2 条工况。采用聚类与Markov 链法 (简称B 法)、聚类法和V-A 矩阵法构建得到的工况与采样数据的数据特征如表6 所示,其误差分别为1.17%、5.80%、9.37%。从数据特征角度表明采用聚类与Markov 链法构建得到的工况与采样数据的误差更小。

表6 数据特征值
基于Cruise 软件搭建了纯电动客车整车模型,对3 条工况及样本数据进行能耗仿真。纯电动客车整车参数如表7 所示。
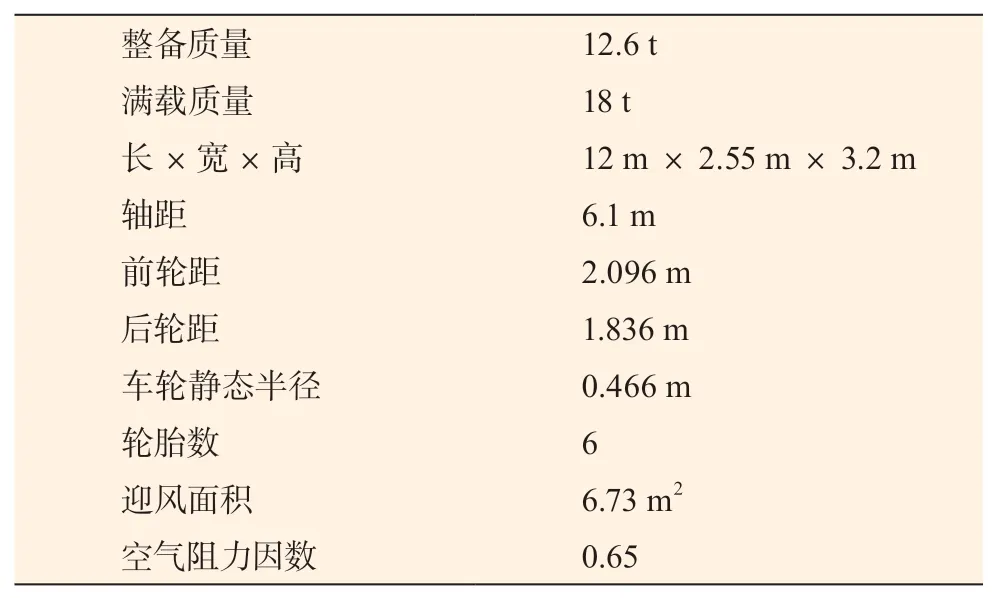
表7 仿真建模所用整车参数
为了避免因工况长度不同带来的影响,将仿真能耗结果换算成百千米电耗。使用样本数据的百千米电耗为72.91 kWh。聚类与Markov 链法结合(B 法)、聚类法和V-A 矩阵法构建工况百千米电耗及与样本数据百千米电耗的偏差率如表8 所示。
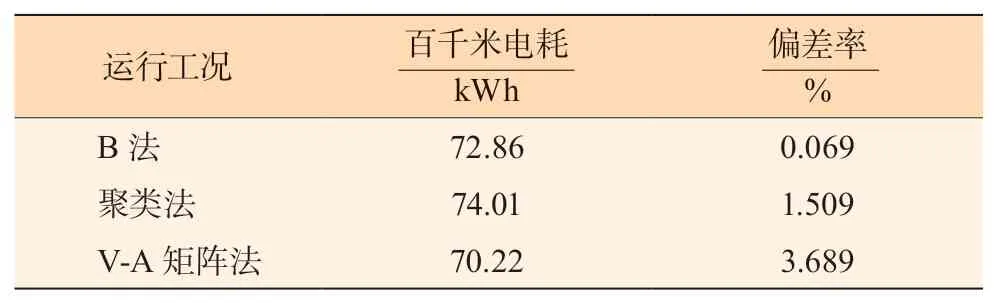
表8 能耗仿真结果
由表8 可知,聚类与Markov 链法构建得到的工况百千米电耗仿真结果为72.86 kWh,与样本数据百千米电耗相差最小,偏差率仅为0.069%,说明利用该方法构建的行驶工况精度更高,更能反映车辆的实际行驶状况,百千米电耗仿真数据也可为该公交线路的运行能耗和驾驶行为经济性评价提供依据。
6 结 论
本文基于聚类与Markov 链结合的方法构建了西安市某线路城市客车的行驶工况,以单位里程比能耗为标准选取典型工况,并与聚类法和V-A 矩阵法构建得到的工况进行了数据特征误差率和仿真百千米电耗对比,得出结论如下:
1) 聚类与Markov 链法中聚类个数和特征参数的选取应以每类短行程个数和状态转移矩阵决定,并不是特征参数选取越多,聚类效果越好。
2) 聚类与Markov 链法工况构建过程中,可根据片段拼接后的V-A 矩阵的欧式距离是否稳定来决定构建工况的长度,从而满足工况构建需求,并减小工况构建及后期应用的工作量。
3) 可定义汽车行驶时的单位里程比能耗作为代表工况选取标准,从能耗角度来筛选代表工况。由此得到的工况与样本数据的数据结构相似度也很高。
4) 数据特征误差率和仿真能耗对比表明:与聚类法和V-A 矩阵法相比,聚类与Markov 链法构建得到的工况与样本的数据特征和能耗结果最为接近。
5) 基于构建得到的工况,后续可开展动力系统匹配选型、混合动力汽车最优能耗及控制策略确定、公交线路的运行能耗、排放及驾驶行为经济性评价研究,并可结合整车模型构建关键零部件的耐久性极限测试工况。
