基于改进F-AHP模型的典型公路边坡稳定性研究

宋春来，李洪艳，朱晓涵

(1.宜昌市轨道交通投资发展有限公司，湖北 宜昌 443002；2.中国葛洲坝集团第二工程有限公司，四川 成都 610091；3.三峡大学土木与建筑学院，湖北 宜昌 443002)

1 概述

在我国中西部地区，路堑边坡分布广泛，其治理、防护已逐渐成为穿山或穿丘陵高速公路建设与运营维护工作中的重大工程问题之一。

国内外专家、学者在路堑边坡工程稳定性研究方面取得了诸多成果。王浩等[1-2]结合边坡稳定度、强度折减法和开挖有限元仿真技术对边坡变形发育演化过程进行了分析和评估，同时对施工的全过程开展数值模拟与优化分析；Adnan Aqeel[3]根据沙特阿拉伯麦地那居民区地质特点分析了岩石路堑边坡的稳定性；Kedir Mohammed Bushira等[4]采用极限平衡法和有限元法对不同形式的路堑边坡稳定性进行了对比分析。还有一部分学者从评价机制的角度进行了分析，王浩等[5]、阮航等[6]考虑到影响路堑边坡稳定性信息的不完整性、随机性和模糊性，结合模糊评判法、专家系数修正和最大隶属度原则，建立了复杂路堑边坡安全评估模型和方法；朱泽奇等[7]通过统计分析分别建立了三类边坡的典型地质概化模型，初步建立了基于深部位移曲线特征的边坡稳定判据；C.Irigaray，R等[8]提出了一种基于GIS技术和概率分析的岩体边坡开挖空间稳定性分析方法。

虽然目前可采用各种方法对路堑边坡进行稳定性分析，但路堑边坡的稳定受多因素耦合作用，因此无论何种评价机制，其结果的准确性在于边坡稳定性影响因素指标的权重。本文基于三峡高速(S58)公路伍家岗收费站路堑边坡，引入三角模糊数以解决在判断风险因素时的含糊性、不确定性和主观性，综合考虑路堑边坡岩土体物理力学性质、地形地貌特征、外界自然因素和人为因素建立改进的F-AHP模型进行稳定性评价，并采用Geo-Slope软件进行边坡稳定性求解，以验证模型的适用性。

2 工程背景

三峡高速(S58)公路位于沪渝高速宜昌城区西延段，起于宜昌市猇亭区高家店枢纽互通，路线向西延伸，先后经过临江溪大桥、伍家岗互通、花艳大桥、宜昌主线收费站，终点在宜昌市东山高新开发区与三峡专用公路顺接。三峡高速伍家岗收费站的东迁，是提升宜昌交通格局的的关键，新收费站拟建场地位于宜昌市伍家岗区，收费广场拓宽和房建区两侧属丘陵、垄岗地貌，地形标高在 57～127 m，相对高差达70 m，地形高差变化较大，其地质剖面如图1所示。

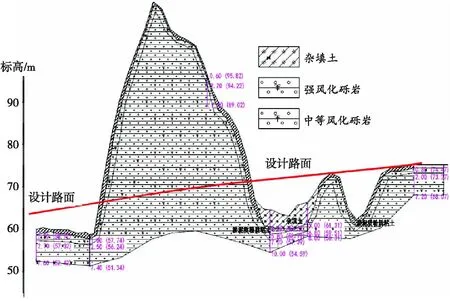
图1 工程地质剖面图Fig.1 Engineering geological section

收费广场道路左侧边坡(见图2)稳定性则是收费站安全建设及运营的重点，须建立一种科学的多因素耦合评判模型，对边坡进行稳定性分析。由勘察结果可知，边坡地层主要由种植土以及强风化、中风化砾岩组成，属岩土质复合边坡。其中种植土呈松散状态，强风化砾岩为散体结构，根据《公路路基设计规范》(JTG D30-2015)确定其边坡岩体类型为Ⅳ类；中风化砾岩为巨厚层状结构，岩体较完整，结构面结合一般，外倾结构面倾角75°，其边坡岩体类型为Ⅱ类。

图2 收费广场道路左侧边坡Fig. 2 Left side of the road slope toll plaza

3 基于三角模糊数改进的F-AHP模型建立

3.1 F-AHP理论

模糊层次分析方法(F-AHP法)是一种分析多因素耦合作用的数学方法。其分析思想可以描述为：首先要从问题全局出发，综合考虑对目标造成影响的全部可能因素；其次，将全部可能因素按照对目标影响的程度进行多层分解；然后，根据因素与因素之间的相互、从属等关系，建立一个多层次的分析模型；最后，计算得出被评价对象的最优评价。具体步骤如下。

1)建立影响因素评价集合U，设有n个评价指标，则数学表达式为：U={u1，u2，…，un}。

2)建立从属集合V，数学表达式为：V={v1，v2，…，vn}。

3)单个因素评价，即构建从影响因素评价集合U到从属集合V的一种关系矩阵。

4)确定因素的权重集合，模糊权向量：A={a1，a2，…，an}

其中∑ai=1，ai≥0(i=1，2，3，…，n)。

5)整合判断矩阵和模糊权重向量矩阵，得到综合评价的评判结果W，即：

6)由上述综合评价计算得出的W进行分析对比。

3.2 三角模糊数理论

F-AHP模型在实际使用中得到的判断矩阵因为未能充分考虑各个因素，故存在很强的离散性与不连续性。但三角模糊数则可很好地解决在判断风险因素时存在的模糊性、不确定性以及评判人的个人主观性。

1)三角模糊数的定义和运算法则。

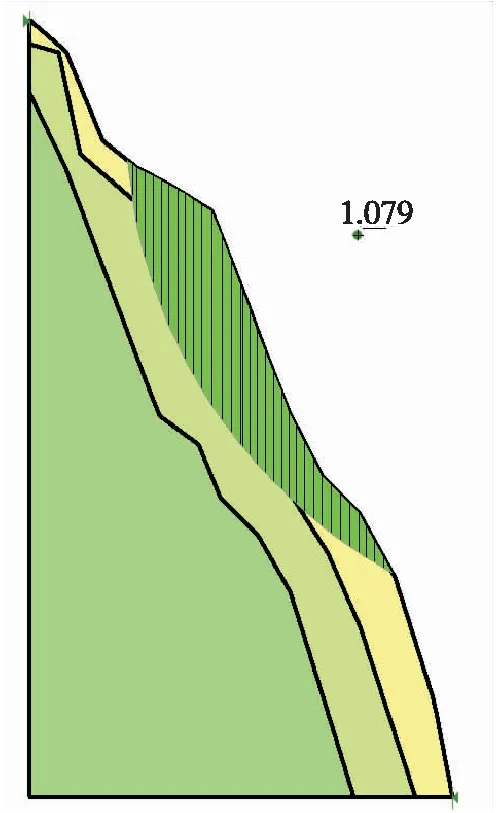
定义1：若p=(l，m，s)，且0

(1)

任意设P1、P2，其中P1=(l1，m1，s1)，P2=(l2，m2，s2)，则P1、P2的计算规则如下：

p1+p2=(l1+l2，m1+m2，s1+s2)

p1×p2=(l1×l2，m1×m2，s1×s2)

λp1=(λl1，λm1，λs1)

定义2：若P1≥P2，则可能度函数可用三角模糊函数，定义为：

v(p1≥p2)=supx≥y⎣min(fp1(x)，fp2(y))」

(2)

v(p1≥p2)=μ(d)=

(3)

2)基于三角模糊数重要性语言标度。一般的层次分析法运用1～9的比例标度，这并不符合人们对于一个常规数字的模糊性描述或者是不确定性的描述。本文选用基于三角模糊数的语言标度来削弱这些影响，具体如表1所示。

3)三角模糊数互反矩阵的确定在判断矩阵P=(pij)中，pij=(lij，mij，sij)，对于任意的i≠j，lij=mij=sij=0.5，且lij+lji=mij+mji=sij+sji=1，则称P=(pij)为三角模糊互不判断矩阵。

3.3 基于三角模糊数的F-AHP的构建

综合3.1节和3.2节的理论，构建基于三角模糊数改进的F-AHP评价模型，该模型分析计算步骤如下。

1)确定所需评价的目标，建立各因素之间的层次结构模型，得到影响因素评价集合，即构建分级评价指标集合。记为U，即U=(U1，U2，…，Un)，其中n为具体的评价指标数量，n=1，2。

2)建立评价结果集合，全部评价者对所评价目标作出的合理的评价结果所组成的集合。记作V，即V={v1，v2，…，vn}。

4)构建权重集合。逐级按结构层次确定指标权重，整合得到总排序权重W，并对判断矩阵进行一致性检验。一致性指标比例记为CR，表达式为CR=CI/RI，若CR≤0.1，表明判断矩阵的一致性通过，若CR>0.1，表明判断矩阵需要修正。

5)最优方案的获取。采用模型T(∧，∨)将总排序权重向量与判断矩阵进行计算，获取最优方案。

4 边坡稳定性评价

4.1 构建评价体系

本文对三峡高速公路伍家岗收费站进城一侧边坡稳定性进行评价，从目标出发综合考虑本工程边坡的岩土体物理力学性质、地形地貌特征、外界自然因素、人为因素等4个指标因素建立评价模型，又因为路堑边坡稳定具有复杂性这一特点，故而每个指标因数又受众多指标影响，同时考虑到无法将所有制约因素均包涵，故而对比参考已有的路堑边坡稳定性评价方案体系，列举了12个主要指标评价路堑边坡的稳定性。本文建立的评价指标体系如图3所示。

图3 路堑边坡稳定性评价指标体系图Fig.3 Circular slope stability evaluation Index system

路堑边坡所属状态为最终目标，即为目标层 A；选取岩土体物理力学性质为B1、地形地貌特征为B2、外界因素为B3以及人为因素B4等4项指标，建立准则层B；再根据权重合理分配的原则，将准则层的每个指标进一步划分为各子指标，建立指标层 C。

4.2 构建模糊判断矩阵

为了综合评价本路堑边坡各因素的优劣，本模型对有多年经验的设计、施工、管理等人员进行随访，通过问卷的形式开展单因素评价。共计发出35张问卷，收回26张，其中可用于评价的表格20张，统计3种状态下各因素所占人数，得到评价结果，如表2所示。

表2 三种稳定状态单因素评价结果表Tab. 2 Three stable state single factor evaluation results

由表2数据计算得到判断矩阵R：

4.3 确立F-AHP权重集

根据构建的判断矩阵R，采用模糊三角数整合专家意见，得出判断数据，并根据式(4)计算一级指标权重dB。

(4)

计算得到：DB1=(0.128，0.199，0.315)，DB2=(0.262，0.433，0.700)，DB3=(0.100，0.165，0.274)，DB4=(0.128，0.201，0.315)。

再根据定义2对DB1、DB2、DB3、DB4去模糊化，得到B1、B2、B3、B4对A的权重dB1、dB2、dB3、dB4，分别为0.094、1、0.043、0.186 ，归一化处理得W0=(0.131，0.707，0.030，0.132)。

将上述计算结果与判断数据整合到一起，如表3所示。

表3 以A为准则的间接优势对比Tab. 3 Comparison of indirect advantages based on A

4.3.1 计算二级指标权重

在元素B1、B2、B3、B4中构建模糊评价矩阵，计算方法与一级指标权重计算方法一致，仅列出B1评价矩阵和权重W1及其一致性检验，如表4所示。

表4 以B1为准则的间接优势对比Tab. 4 Comparison of indirect advantages based on B1

4.3.2 确定指标层相对于目标层的权重

前一小节的分析计算到了某一层次全体元素对上层某一元素的重要性排序。同理，在单排序的基础上对总目标进行总排序，可获取同一层次全体元素对总目标的重要性排序。各指标层相对于目标层的权重Wi见表5。

表5 各指标层相对于目标层的权重WiTab. 5 The relative weight of each index layer to the target layer Wi

4.3.3 确定综合评价结果

通过T(∧，∨)模型 计算，得到计算权重W对应的综合评判矩阵C：

将C归一化得C′=(0.321 0，0.407 4，0.271 6)

由归一化结果可知：本边坡处于较稳定状态的概率最大为 40.74%，处于稳定状态的概率为 32.10%，处于不稳定状态的概率为27.16%。根据最大隶属度原则判定，本边坡处于较稳定状态。

5 Geo-SLOPE稳定性验证

在路堑边坡的稳定性数值计算中软件Geo-Studio有着广泛运用[9]。然而边坡稳定常采用极限平衡条分法进行分析计算[10]，其中极限平衡条分法又包括瑞典圆弧法、毕肖普法、摩根斯坦-普拉斯法、沙尔玛法等方法。本文计算采用滑裂面为任意形式且收敛性好的摩根斯坦-普拉斯法。

根据地质勘查报告绘制计算模型图并导入Geo-slope计算软件，地层参数按表6数据取值，计算得到天然状态下的最危险滑动面及稳定系数，如图4所示。

表6 地层物理力学参数表Tab.6 Physical and mechanical parameters of the formation

图4 天然状态下最危险滑动面及稳定系数Fig. 4 The most dangerous sliding surface and stability coefficient in the natural state

由图4分析可知：在天然状态下边坡的安全稳定系数为1.079，处于较稳定状态，与上一节所建立的改进模糊数学评价模型所得结果一致。

6 结论

1)引入三角模糊数的理论，解决了在进行路堑边坡稳定性评判时风险因素的含糊性、不确定性和主观性，弥补了层次分析法在实际工程运用中的不足，为路堑边坡稳定性的评判提供了一种受众面广的科学方法，相比于数值计算更具普适性。

2)基于三角模糊数构建了改进的F-AHP路堑边坡稳定性评价模型，并将此模型运用于三峡高速(S58)公路伍家岗收费站段路堑边坡的稳定性评价。根据最大隶属度原则表明此路堑边坡为较稳定状态，其概率为40.74%，处于稳定状态和不稳定状态的概率分别为 32.103%和27.16%。

3)根据勘察资料建立了路段边坡的有限元计算模型，导入Geo-Studio中的SLOPE/W模块求得安全系数为1.079，由此判断此路堑边坡处于较稳定状态，与数学评价模型评价结果一致。由此结果进一步佐证了所构建的改进的F-AHP模型的正确性与合理性。