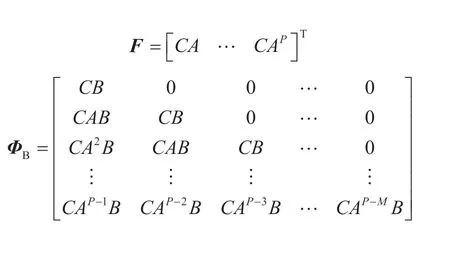基于模型预测控制的光储发电系统VSG频率控制方法

2022-07-15李帅虎胡耀尹罗滇生张志丹

智能电网 2022年4期

李帅虎，胡耀尹，罗滇生，张志丹

（1．长沙理工大学电气与信息工程学院，湖南省长沙市 410114；2．湘潭大学自动化与电子信息学院，湖南省湘潭市 410015；3．湖南大学电气与信息工程学院，湖南省长沙市 410082；4．国网湖南省电力公司电力科学研究院，湖南省长沙市 410004）

0 引言

国家提出“双碳”目标背景下，以新能源为主体的电力系统建设将正式铺开，“十四五”期间以光伏、风电为主的新能源装机规模将大幅增长。光伏发电作为其重要组成部分，自2021年6月20日光伏整县推进政策发布至2021年9月，全国共22个省上报了约500个示范县，总规模超过100 GW，未来分布式屋顶电站总体市场规模将达800 GW以上[1-3]。大量分布式光伏电站接入对配电网的消纳能力和稳定运行将产生较大影响，而且光伏发电都由并网逆变器接入电网，这类电力电子装置转动惯量与阻尼小，使电网应对功率波动的支撑能力变弱，导致新能源电网的频率和电压稳定性受到严峻考验[4-5]。如果没有有效的解决方案，或将直接影响整县推进政策的落地。

在此背景下，有学者提出了虚拟同步发电机（virtual synchronous generator, VSG）技术，使光伏发电系统模拟同步发电机的运行特性，有效改善了新能源电网的稳定性。文献[6]提出了一种由线性化系统模型特征值灵敏度矩阵引导的VSG参数整定方法，该方法以迭代优化的形式确保了系统稳定性，并使系统特征值从关键点移开，改善了传统的参数整定方法在低开关频率下效果欠佳的弊病和动态性能。为了改善VSG暂态响应特性，文献[7]利用速度反馈系数，提出了VSG虚拟转动惯量自适应调控方法，大幅减小惯量的调节量，保证频率变化不超过阈值的同时抑制功率超调。文献[8]针对复杂电网工况下的VSG，在提升其并网稳定性、故障穿越能力、减少电量损耗的同时改善了其频率特性。文献[9]建立了以频率变化率为判断条件的自适应函数控制方法，可根据动态过程中输出频率暂态波动引起的频率变化率的变化进行自适应调节，保证了控制的灵活性。上述研究成果实现了VSG参与系统的一次调频，当发生较小的功率变化时可有效阻止系统频率的快速变化，维持系统频率稳定，但是一旦系统发生较大的负荷扰动，频率变化可能超出安全运行的限制范围[10]。

由此，光伏阵列与储能电池并联的电压源型VSG被提出[11-13]，其能够有效提高并网点母线电压和频率的支撑能力，但是其对储能系统性能过于依赖，尤其对储能系统可靠性的要求非常高。为了解决此问题，有学者提出将光伏阵列和储能系统各自独立并入电网的结构，使其灵活性更高，同时可实现在光储系统并网运行中模拟同步发电机的外特性，能动态支撑由于功率波动或负载变化等扰动引起的母线频率波动[14]。此类结构在交流侧实现VSG控制功能，可降低控制功能对储能的依赖。以上频率响应控制策略的核心在于需要利用转子角频率的变化率对惯量和阻尼进行实时调整，然而其控制系统的输出量总是依照前一次采样的变化率来确定，控制策略的作用总是滞后于系统的变化，就可能出现即使VSG实现了一、二次调频，也无法减小频率变化幅值的现象[15-18]。

为提高VSG并网逆变器的二次调频能力和运行性能，本文建立光储并网发电系统模型，其中光伏并网采用双级式结构实现并网功率控制，储能逆变器实现模型预测控制（model predictive control, MPC）的VSG频率控制方法。该方法首先通过转子运动方程和下垂控制方程建立了VSG的可优化模型，并对该模型进行离散化，再利用MPC得到转子角频率的运动轨迹，取最优的预测控制输入向量的第一项作为下一时刻控制器的反馈输入。通过构建的转子角频率增量与转矩增量间的反馈通道，对频率偏差进行实时预测补偿，提升VSG并网逆变器的二次调频能力和运行性能，改善其并网时的系统频率调节效果。

1 光储并网发电系统的结构

光伏阵列和储能系统各自独立并入电网的光储发电系统结构如图1所示[14]。

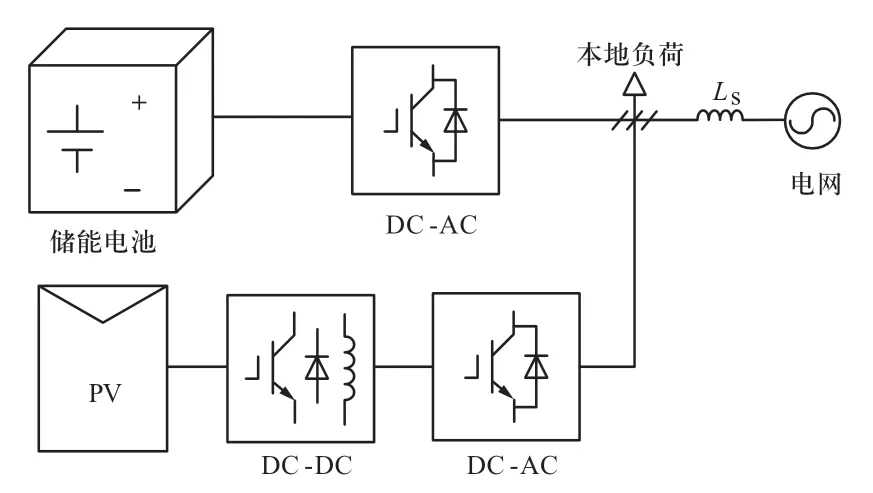
图1 光储独立并入电网的发电系统结构Fig. 1 Structure of photovoltaic system with storage

光伏发电系统中DC-AC并网逆变器采用传统的PQ并网功率控制，DC-DC直流升压变换器采用最大功率点跟踪控制策略。储能电池由独立的并网逆变器并入电网。光伏发电单元与储能单元以功率互补的方式联系起来，并由储能逆变器在交流侧实现VSG控制策略。该系统可以实现惯性和阻尼的引入，在发电功率与电网负载变化时光储系统参与电网的频率和电压调节，在暂态过程中支撑系统频率与电压。此外，若储能并网逆变器失效，光伏发出功率仍能通过其独立的逆变器输送给电网，减小了VSG控制功能对储能系统可靠性的依赖。

2 光储系统的控制策略分析

根据图1所示的光储并网发电系统结构，PV并网逆变器采用电流型PQ控制策略，利用PI调节器调节电压和电流，从而实现有功功率和无功功率的解耦控制。

2.1 VSG的频率控制策略分析

传统的同步发电机（后文简称为发电机）一般采用二阶模型描述，则图1中储能系统等效VSG转子运动方程[17]如下：

式中：J表示发电机的转动惯量；kD为同步发电机阻尼力矩对应的阻尼系数；Te、Tm和TD分别代表发电机的电磁转矩、机械转矩和阻尼转矩；Tm=Pm/ω0；Te=Pe/ω0；Δω=ω-ω0；Pm是发电机的机械功率，Pe是发电机的电磁功率；t代表系统运行时刻；ω代表发电机的角速度；ω0是发电机的额定角速度。

根据同步发电机通过控制原动机的机械转矩来调节发电机有功功率输出的原理，VSG控制框图如图2所示。其中，R为电阻，L为电感，iref为并网逆变器机端电流有效值的指令值，f0、f分别为参考频率与实际频率，ΔEU为极端电压调节单元的输出电势，Uref、U分别为并网逆变器极端电压有效值的指令值和真实值，Qref为并网功率指令，u为机端电压，PR为比例谐振控制器。

VSG的有功-频率环节模拟了传统同步发电机的机械部分，利用下垂控制模拟调速器环节，通过调节Tm实现VSG有功指令的调节。Tm由机械转矩T0和频率偏差反馈转矩ΔT两部分组成；kf为调频系数。VSG的无功-电压环节模拟了传统同步发电机的励磁部分，图2（c）中kq为无功调节系数，同时在无功输出参考值Qref和无功输出实际值Q的共同作用下得到对应无功调节电压ΔEQ；kv为电压调节系数，在Uref和U的共同作用下得到对应无功调节部分的机端电压调节单元输出的补偿电压ΔEU；E0为VSG空载运行时的电势。上述三部分电压共同构成虚拟同步发电机的虚拟电势E。

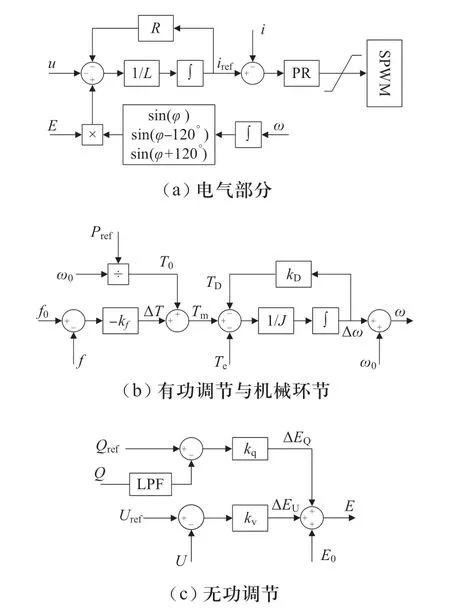
图2 虚拟同步发电机控制框图Fig. 2 Control block of VSG

2.2 VSG的频率调节

储能系统通常利用逆变器的下垂控制策略调节有功以维持频率的动态稳定。一旦系统中发生功率扰动，系统频率也会随之变化。调节的下垂系数kp由发电机功率变化量和角频率变化量共同确定，决定了功率与角频率间的静态关系，表示为

式中：ΔP为VSG输出功率的变化量。由式（2）可知，若负荷增加，系统角频率下降，功率偏差ΔP随之增大，减缓由负荷增加所带来的角频率偏差；反之，若负荷减小，下垂控制减少输出功率，降低机组出力。可以看出，VSG的调频思路是将下垂控制的有功反馈量作用于转子运动方程上，以此构建频率偏差与输入转矩之间的关系。然而下垂控制的有功频率控制仅参与系统的一次调频，无法消除频率静差。

3 基于MPC的VSG反馈控制方法

3.1 建立VSG可优化模型

依据第2.2节VSG控制原理，若忽略PWM环节时滞影响，则系统机械特性仅由式（1）决定。但是该模型中未建立状态变量Δω与输出变量之间的关系，所以该模型无法实现有效控制。本文考虑安全限制、装置运行环境等不确定因素对并网逆变器控制器的影响，例如发电侧出力变化、网侧波动等都会导致偏差的进一步扩大，造成对控制系统运行性能的影响。将电磁转矩改变量ΔTe视为扰动输入，利用输出方程式（2）的下垂系数和转子运动方程式（1）的线性化方程构建VSG的可优化模型状态空间方程，如式（3）所示。

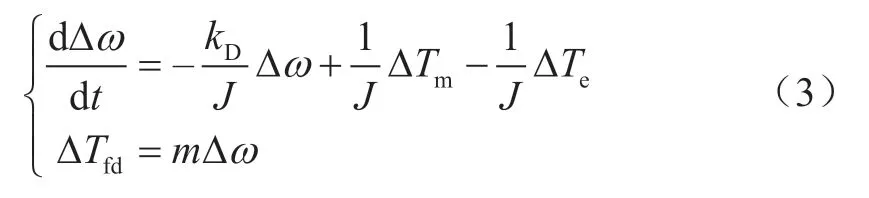
式中：ΔTfd=ΔP/ω0，为状态变量；ΔTm为控制输入；ΔTfd为反馈偏差转矩；m为角频率静态特性系数，反映输出转矩增量与角频率增量之间的静态特性关系，m=kf/ω0。此时，该可优化模型在满足控制要求的同时，也反映了状态变量与期望的输出转矩间的关系。

3.2 MPC-VSG控制方法

本文根据MPC方法的基本原理[19]，对式（3）进行离散化，可得

式中：x(k＋1)为k＋1时刻的预测值；x、u、d、y分别表示Δω、ΔTm、ΔTe、ΔTfd；A=-kD/J；B=-D=1/J；C=m。

以式（4）作为预测模型，设从当前k时刻起，系统输入发生M步变化，之后保持不变，P、M分别表示预测时域和控制时域，且P≥M。由式（4）可预测出在u(k+1)，u(k+2)，…，u(k+M)的作用下，k+j(j=1，2，…，P)时刻转子角频率为

由于VSG频率响应优化的目的是得到最优的输入转矩向量，所以可以通过当前k时刻和预测时刻Δω的值，求得下一时刻ΔTm的给定值。其中k时刻的状态优化主要是确定k时刻起的M个控制量u(k)，…，u(k＋M－1)，其向量形式如下：

式中：Yref为转矩期望值所构成的给定向量；Y为转矩实际值所构成的向量；控制量Q、R是状态空间方程系数矩阵的对角阵，分别被称为误差权矩阵和控制权矩阵。

为求解式（6），通过二次规划求解过程可得下一时刻的预测控制输入向量ΔU的最优解表达式为

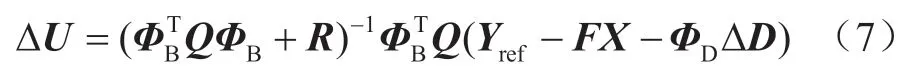
式中：X为状态变量组成的向量；F为预测域内阻尼惯量比系数组成的向量；ΔD为临近两个时刻ΔTe的差值；参数F、ΦB、ΦD的计算式见附录A。

根据滚动时域原则，取预测控制输入向量的第1项作为下一时刻VSG的反馈输入。由式（7）可得

3.3 VSG反馈控制器结构

将式（8）代入式（4）推导可得基于MPC的VSG反馈控制方程，如式（9）所示：

分析式（9）可知，本文提出的反馈控制过程考虑了VSG的惯量和阻尼特性，通过改变KT、Kω、Ke参数的取值改善对系统的频率控制特性。k+1时刻的反馈转矩的大小与输入变量仅为线性关系，且减小了输入变量间的耦合关系，即当某个输入回路出现较大的扰动时，只需调整对应回路的参数即可实现对偏差的补偿。

依据上述反馈控制方法，MPC-VSG反馈控制器的控制结构如图3所示，即在图2（b）的传统控制策略的基础上取消了下垂控制环节，增加了MPC反馈控制环节。

图3 控制系统结构图Fig. 3 Structure diagram of control system

由于频率f与角频率ω之间的线性关系，增加了MPC反馈控制器后，若系统出现频率偏差，则此时MPC控制器目标函数≠0，滚动优化环节会在未来多个时刻进一步调整反馈偏差转矩。而反馈偏差转矩与实际偏差转矩作差（E0-Ee），其差值输入至惯性环节，可实现对偏差电磁转矩的跟踪。通过跟踪电磁转矩的变化量，可应对并网逆变器参数变化和系统模型非线性等因素带来的外部扰动，使得系统输出更加稳定。此外，MPC输出的反馈偏差转矩也会使得目标函数最小，可补偿系统有功功率的差额，实现对频率的无静差控制。

4 仿真分析

为验证本文提出的基于模型预测控制的光储发电系统VSG频率控制方法的有效性与正确性，本文在 MATLAB/Simulink平台搭建如图1所示的光储系统仿真模型。其中，储能本体铅酸蓄电池容量为100 Ah，其额定工作电压是200 V，初始荷电状态是80%，蓄电池最大稳定输出功率是40 kW，其他主要参数见表1[14]。光伏发电系统由500块光伏电池板组成，每块光伏电池板的最大功率输出为213 W。光伏发电系统采用扰动观察法对光伏系统进行最大功率跟踪，因此恒定条件下光伏发电系统的输出功率不变。设置光伏并网系统的光照强度为1000 W/m2，温度为25 ℃，此时光伏并网功率近似为100 kW。

表1 VSG并网逆变器仿真参数Table 1 VSG grid-connected inverter simulation parameters

4.1 储能系统动态响应分析

初始时刻设置光储系统以120 kW/0 kvar的调度功率指令运行，则储能系统的功率指示值为20 kW。0.4 s时在光储系统的输出侧接入或切除40 kW的负载，应用传统VSG控制策略与基于模型预测控制的VSG控制策略时的光储系统的输出有功响应分别如图4、图5所示。

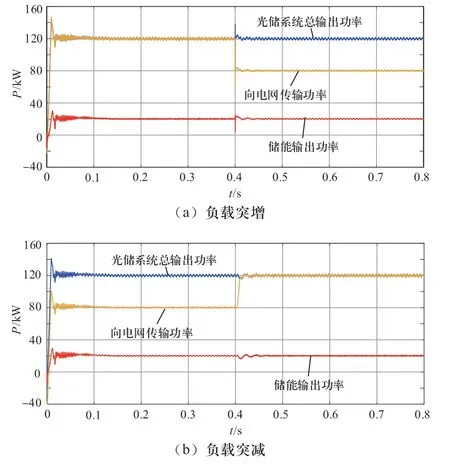
图4 应用传统VSG控制策略时光储系统有功响应曲线Fig. 4 Output active power response of photovoltaic system with storage under traditional VSG strategy

由图4（a）可知，初始时刻光储系统按照调度功率指示值输出120 kW的功率，其中，光伏发电系统输出功率为100 kW，而储能系统输出功率为20 kW。在0.4 s光储系统的输出侧投入40 kW负载时，光储系统的总输出功率以及储能的输出功率都出现短暂上升趋势，在0.015 s后恢复至原有水平。由于40 kW负载的增加，0.4 s时刻光储系统向电网传输的功率将由120 kW调整至80 kW。而在图4（b）中，40 kW负荷切除时，电网吸收功率由80 kW升至120 kW，光储系统的功率调节时间约为0.15 s。

图5中光储系统的有功响应波形与图4相差不大，负荷切换时基于模型预测控制的VSG控制策略对功率的调节响应速度较快。可以发现，由于引入了VSG控制策略，上述两种策略都能在负载变化时利用储能系统为电网提供虚拟惯性以及阻尼，因此负载波动对电网造成的影响较小。

图5 应用基于模型预测控制的VSG控制策略时光储系统有功响应Fig. 5 Output active power response of photovoltaic system with storage under MPC-based VSG strategy

设置光储系统以120 kW/0 kvar的调度功率指令运行， 0.4 s在光储系统的输出侧直接接入或切除40 kW负载。在常规VSG控制策略与基于模型预测控制的VSG控制策略控制下光储系统的频率响应曲线如图6所示。

图6 光储系统频率响应曲线Fig. 6 Frequency response of photovoltaic system with storage

在图6（a）中可以发现，应用传统VSG策略时，正向功率变化使得电网频率存在0.07 Hz的频率波动，在0.17 s左右电网频率恢复至50 Hz；随后，在0.4 s时刻光储系统输出侧突增40 kW负载，系统频率下降至49.87 Hz，在0.12 s后才能恢复到50 Hz。而应用基于模型预测控制的VSG控制策略时，启动时系统频率波动仅为0.04 Hz，恢复时间为0.13 s；负载突增时系统频率波动仅为0.06 Hz，恢复时间为0.09 s。

在图6（b）中，应用传统VSG策略时，正向功率变化使得电网频率存在0.08 Hz的频率波动，在0.25 s左右电网频率恢复至50 Hz；随后，在0.4 s时刻切除光储系统输出侧40 kW负载，系统频率上升至50.12 Hz，在0.11 s后恢复到50 Hz。而相同的负荷条件下，应用基于模型预测控制的VSG控制策略时系统频率响应速度增加，系统频率波动幅值以及时间都进一步减小。

对比分析图4以及图5波形可知，储能逆变器采用VSG控制策略后，光储系统可快速准确地对调度功率指令进行响应，并为系统提供一定的惯性与阻尼，从而提高整体的控制性能。在负荷突然增大或减小的情况下，光储系统并网功率能快速随之做出响应变化。此外，对比图6中常规VSG控制策略与基于模型预测控制的VSG控制策略控制下光储系统的频率响应曲线，显然基于模型预测控制的VSG控制策略频率响应速度更快。所提策略可有效减小功率波动对系统频率的冲击，对维持系统稳定具有重要意义。