大型数控成形磨齿机床装配误差-齿面误差研究*

丁文政，张 虎，王 娟，贺文权

（1.南京工程学院，南京 211167；2.南京工大数控科技有限公司，南京 211816；3.江苏经贸职业技术学院 ，南京 211168）

大模数硬齿面精密齿轮广泛应用在能源电力、航空航天和海洋船舶等战略装备中，齿面误差关系到齿轮的传动精度、传动效率和传动噪音等关键性能指标。磨削是加工硬齿面齿轮最主要的精加工工艺，相比于展成磨削，成形磨削有足够的自由度可以进行齿面廓形修形和螺旋线修形，提升齿轮的传动性能，因而更适合于精加工大模数齿轮；同时成形磨削中，由于砂轮和齿轮之间是线接触，加工大模数齿轮效率更高[1]。2020年我国齿轮产品达到2800亿元，规模位居世界第一，但高档大型数控成形磨齿机床主要被Gleason和KAPP NILES等国外厂商垄断，制约了我国向齿轮制造强国的发展。

目前，国产大型数控成形磨齿机床已有应用，但磨削齿面精度与国外机床相比仍有差距。学术和工程界为此也开展了大量的工作，主要包括4个方面。（1）通过热误差补偿提高机床的磨齿精度，Wang等[2]建立了大型数控成形磨齿机床传动链的热误差理论模型来指导误差补偿；阳辉等[3]研究了刀具热误差对齿距误差的影响规律，提出跨齿分度加工方法来降低齿距误差。（2）聚焦于运动控制以及砂轮和工件的安装参数调整，张虎等[4]以齿面实际拓扑偏差与目标拓扑偏差差值最小为目标，优化磨齿机床的五轴运动控制，有效地减小了齿向修形产生的齿面扭曲；郭二廓等[5]建立了成形磨齿齿向修形误差评价模型，提出了调整砂轮和工件安装参数的优化方法，有效减小了斜齿轮齿向修形误差。（3）合理选取砂轮安装角和砂轮半径，丁国龙等[6]通过计算砂轮曲面和齿轮螺旋面间接触线上任意点诱导法曲率值检验磨削是否干涉，以磨削无干涉为限制条件获得砂轮安装角和砂轮半径的取值范围；李腾等[7]对成形砂轮接触线进行研究，精确计算出最优砂轮安装角，提高了加工效率，避免了极端情况下的磨削干涉。（4）构建数控成形磨齿机床几何误差模型，对几何误差进行预测和补偿[8-9]，丁爽等[10]基于齐次坐标变换矩阵方法建立了五轴机床装配误差模型，并通过逆向解耦运算，在NC代码中进行误差补偿；赵飞等[11]分析了数控机床进给系统装配误差对运动精度的影响，并以此评估数控机床的运行状态，以上研究均未涉及成形磨削齿面误差；夏长久等[12]建立了五轴成形磨齿机床几何误差与齿面误差模型，并通过敏感性分析法识别出关键误差和敏感部件，但未关注磨齿机床的装配误差。

精密磨齿机床对装配误差要求极为苛刻，一味通过收紧零件公差控制装配误差会使零件加工成本急剧上升，甚至无法加工；另外国产机床的装配工艺也缺乏定量化指导，批量生产的机床精度一致性得不到保证[13-16]。现有的数控成形磨齿机床几何误差模型是基于砂轮和工件之间的位姿偏离，无法直接反映成形磨削齿面误差，如何根据齿轮齿面精度要求精准控制装配中的主要几何误差是亟需解决的问题。

为此，本研究基于齿面成形磨削过程中砂轮与工件之间的共轭运动关系，利用曲面族包络理论，建立包含装配几何误差的成形磨削齿面模型，提出实现磨削齿面误差评价的流程方法，定量分析关键装配几何误差对成形磨削齿面误差的影响；然后根据分析结果和齿轮齿面精度要求，优化分配各装配几何误差；最后进行机床装配精度调整和齿轮成形磨削试验。

1 包含装配几何误差的成形磨削齿面建模

1.1 磨削系统装配几何误差

如图1所示，大型数控成形磨齿机床有4个直线轴和2个旋转轴，分别是沿着立柱移动方向的X轴、平行于砂轮旋转轴的Y轴、平行于工件旋转轴的Z轴、平行于砂轮径向的W轴、磨削主轴摆动A轴和工件旋转C轴。另有3个主轴分别是磨削主轴SP1、修整主轴SP2和SP3。这些部件又被分成两个系统：齿轮磨削系统和砂轮修整系统。齿轮磨削系统包括X轴、Y轴、Z轴、A轴、C轴和SP1主轴。砂轮修整系统包括Y轴、W轴、SP2主轴和SP3主轴。磨齿之前，Y轴和W轴联动，用金刚滚轮修整砂轮；然后将X轴运动到砂轮和齿轮的理论中心距位置，Y轴运动到零位，A轴偏转一个和螺旋角相适应的角度；最后Z轴和C轴联动走螺旋线，完成一个磨削冲程。其中齿轮磨削系统的运动链长，影响齿面误差的装配几何误差众多，是本文的主要研究内容。

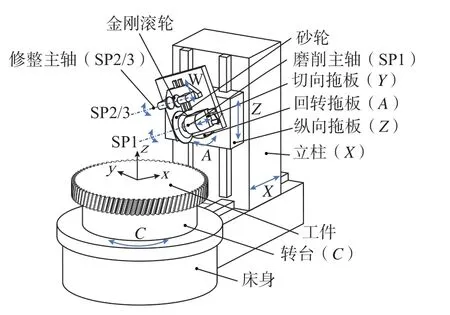
图1 大型数控成形磨齿机床结构图Fig.1 Schematic of a large-scale CNC gear profile grinding machine

图2是成形磨削系统运动链，为了研究磨削系统装配几何误差对齿面误差的影响，建立图3所示的各部件在装配几何误差影响下的坐标系转换来描述成形磨削中各主要部件之间的空间位置关系。

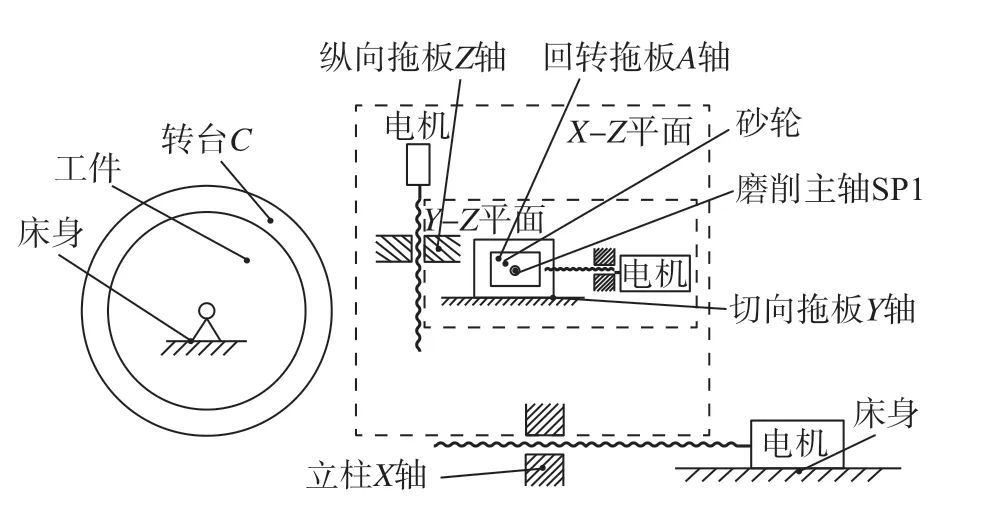
图2 成形磨削系统运动链Fig.2 Kinematic chain of profile grinding system

图3中S表示坐标系，S下标中的数字分别表示的部件1为转台； 2为工件； 3为立柱X轴； 4为纵向拖板Z轴； 5为回转推板A轴； 6为切向拖板Y轴； 7为磨削主轴SP1； 8为砂轮。连在数字后的字母s和d分别表示该部件的静止和运动坐标系；S下标中的其他独立字母a、b、c、d表示的是辅助坐标系。磨削系统装配中的主要几何误差编号和实际物理意义见表1。

表1 磨削系统装配几何误差Table 1 Assembly geometric errors of profile grinding system

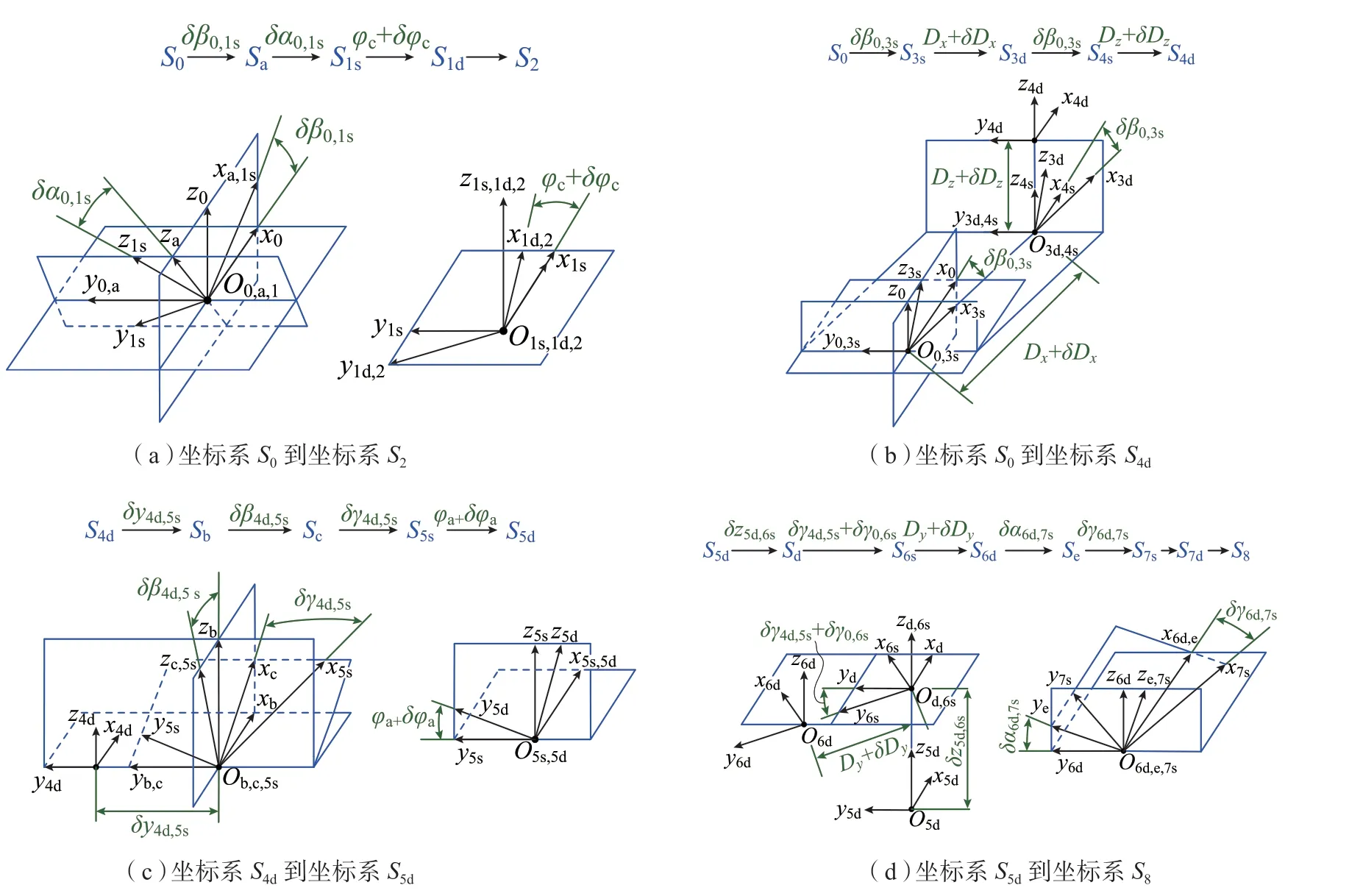
图3 成形磨削系统装配几何误差与坐标系Fig.3 Assembly geometric errors and coordinate systems of profile grinding system

1.2 成形磨削运动建模

齿面成形磨削的过程，可以用磨削运动中砂轮相对于工件位置和姿态的数学模型来描述，该模型包含了上述的装配几何误差，表示为

式中，各个相邻坐标系统的坐标变换矩阵，可以依据图3中坐标系之间的关系得到。

式（1）中，砂轮曲面r8(u,θ)可以由砂轮的轴向廓形绕砂轮的回转轴线旋转而成。如图4所示，xf(u)和yf(u)是砂轮轴向廓形h-h′在砂轮轴向坐标系Sf中的坐标。初始时砂轮轴向坐标系Sf和砂轮坐标系S8重合，当砂轮轴向坐标系Sf绕y8轴旋转时，曲线h-h′在砂轮坐标系S8中扫掠出砂轮曲面。砂轮曲面可以表示为

图4 砂轮轴向廓形扫掠出砂轮曲面Fig.4 Wheel surface swept by its axial profile

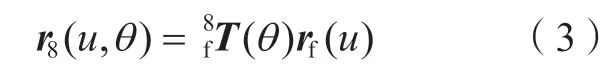
式中，rf(u) =[xf(u),yf(u),0,1]T，

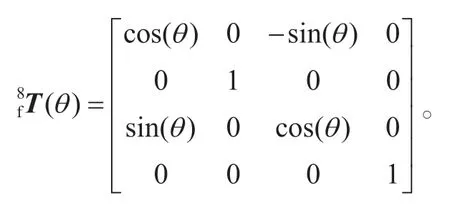
1.3 成形磨削齿面建模

最终成形磨削出的齿面是砂轮单参数曲面族r2(u,θ;t)的包络，为了研究装配几何误差对磨削齿面误差的影响，这里忽略砂轮修整误差，来求解r2(u,θ;t)曲面族的包络面。思路是建立曲面族与包络面的接触条件，然后依据接触条件计算出曲面族上与包络面相切接触的公共点，将这些点提取出来，即可得到包络面。为此，首先将式（1）中齐次变换矩阵改写成旋转变换矩阵R(t)和平移向量的P(t)组合，从而将式（1）变为

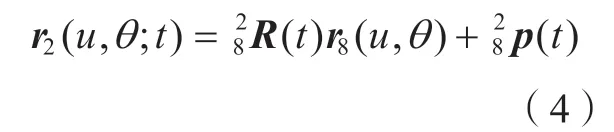
然后，依据空间曲面啮合原理，砂轮曲面族与包络面之间的接触条件应满足

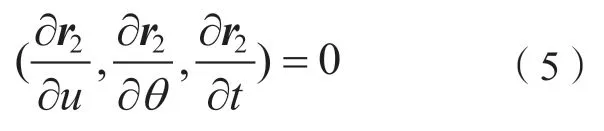
从而得到砂轮曲面族的包络面为

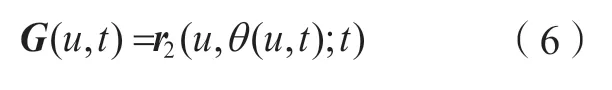
2 成形磨削齿面误差评价

为了评估磨削系统装配几何误差对成形磨削齿面误差的影响，需要对求得的包络齿面进行误差评价。图5（a）中，理论齿面上有一系列的虚线网格，相交形成很多网格点，每个网格点由字母和数字组成。同侧齿面上数字相同、不同的一系列网格点形成的纵向曲线称为齿向曲线。同侧齿面上字母相同、数字不同的一系列网格点形成的横向曲线称为齿廓曲线。齿廓曲线是齿面与端面的截线，齿向曲线是齿面与圆柱面的截线。目前的齿轮评价标准（ISO∶1328—1∶2013、GB/T 10095.1—2008）都是基于齿廓曲线和齿向曲线的，没有针对整个齿面的评价标准。为了依据现行标准评价磨削齿面的精度等级，必须求出齿廓曲线和齿向曲线的误差。图5（a）中一系列的齿廓曲线和齿向曲线组成的网格称为拓扑网格，所有网格点处包络齿面与理论齿面的误差称为磨削齿面误差，大小是式（6）中G(u,t)与理论齿面之间的差值。

每一点的计算如图5（b）所示，成形磨削齿面上G5′与理论齿廓上点G5对应，理想的情况是在理论齿面上每个网格点处，在端面法向上计算成形磨削齿面上对应点到该点的误差。也就是先确定G5的坐标，然后计算G5′的坐标，再计算两点的差值。由于磨削形成的包络齿面没有解析表达式，只能计算得到齿面上很多的离散数据点，为了得到点G5′的坐标必须对离散的磨削形成齿面进行曲面拟合，然后在拟合曲面上计算点G5′的坐标，由于曲面拟合的精度很难达到0.001mm，导致计算得到的G5′坐标误差较大。本文先将磨削形成包络面上的每个离散点在端面内向理论齿面做垂线，由于理论齿面是有解析表达式的，这样可以容易求得对应的理论齿面上的点，再计算两者的误差，然后对这些误差进行拟合和插值，得到网格点处的误差。按照这一方法，可以分别计算出齿廓形状偏差ffα、齿廓倾斜偏差fHα、螺旋线形状偏差ffβ、螺旋线倾斜偏差fHβ，以及齿厚偏差fsn，并对齿轮精度等级进行评价。

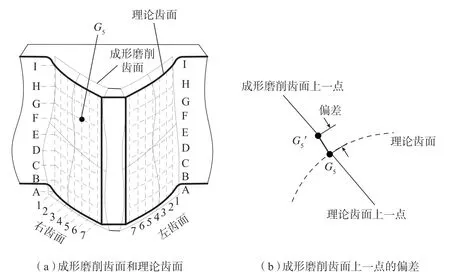
图5 成形磨削齿面与理论齿面之间的偏差Fig.5 Deviations between profile grinding tooth surface and theoretical tooth surface

基于上述模型和误差评价方法，可分析表1所列15项装配几何误差对磨削齿面误差的影响，评价流程如图6所示。主要包括3个步骤：首先计算砂轮的理论廓形rf(u)和坐标变换矩阵；然后计算接触方程θ=θ(u,t)，并将结果代入曲面族，得到磨削形成包络面r2(u,θ(u,t);t)；最后对成形磨削齿面进行误差评价。

图6的误差评价流程中包括A、B、C3个循环过程。A循环过程为在坐标变换矩阵定的情况下，对砂轮廓形上每一点（不同参数u）计算接触方程，得到一系列接触点。这些接触点形成一条曲线，表示磨齿过程中某一时刻，砂轮与实际齿面的接触线。B循环过程包含A循环过程，对磨齿过程的不同时刻，分别求得接触线，这些接触线就是磨削形成的包络面。C循环过程包含B循环过程，分别为不同的误差项设置合理的误差值，得到不同的磨削齿面，并对每个磨削齿面进行误差评价。

3 计算分析与试验

3.1 单值计算分析

某一齿轮成形磨削、齿轮、砂轮规格以及相关参数见表2。按照图6所示的流程，分析表1中每个误差项所产生的磨削齿面误差。表1中长度类误差项的数值设为0.2mm，角度类误差项的数值设为200arcsec。图7为各误差项对应的齿面拓扑误差图，其中fHα1和fHαr分别表示左右齿面中最大的齿廓倾斜偏差；fHβ1和fHβr分别表示左右齿面中最大的螺旋线倾斜偏差；fs为齿面中心点对应的齿厚偏差。此外，15个误差项产生的齿廓形状偏差和螺旋线形状偏差均接近为0。

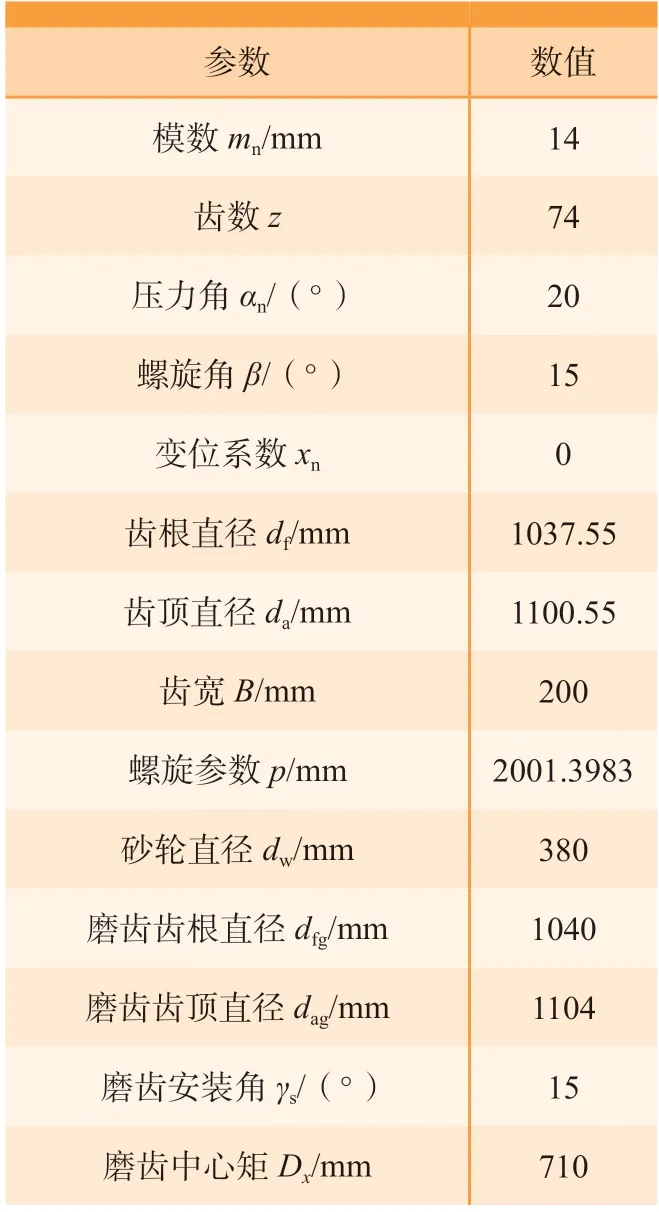
表2 磨齿的基本参数Table 2 Basic parameters for gear grinding

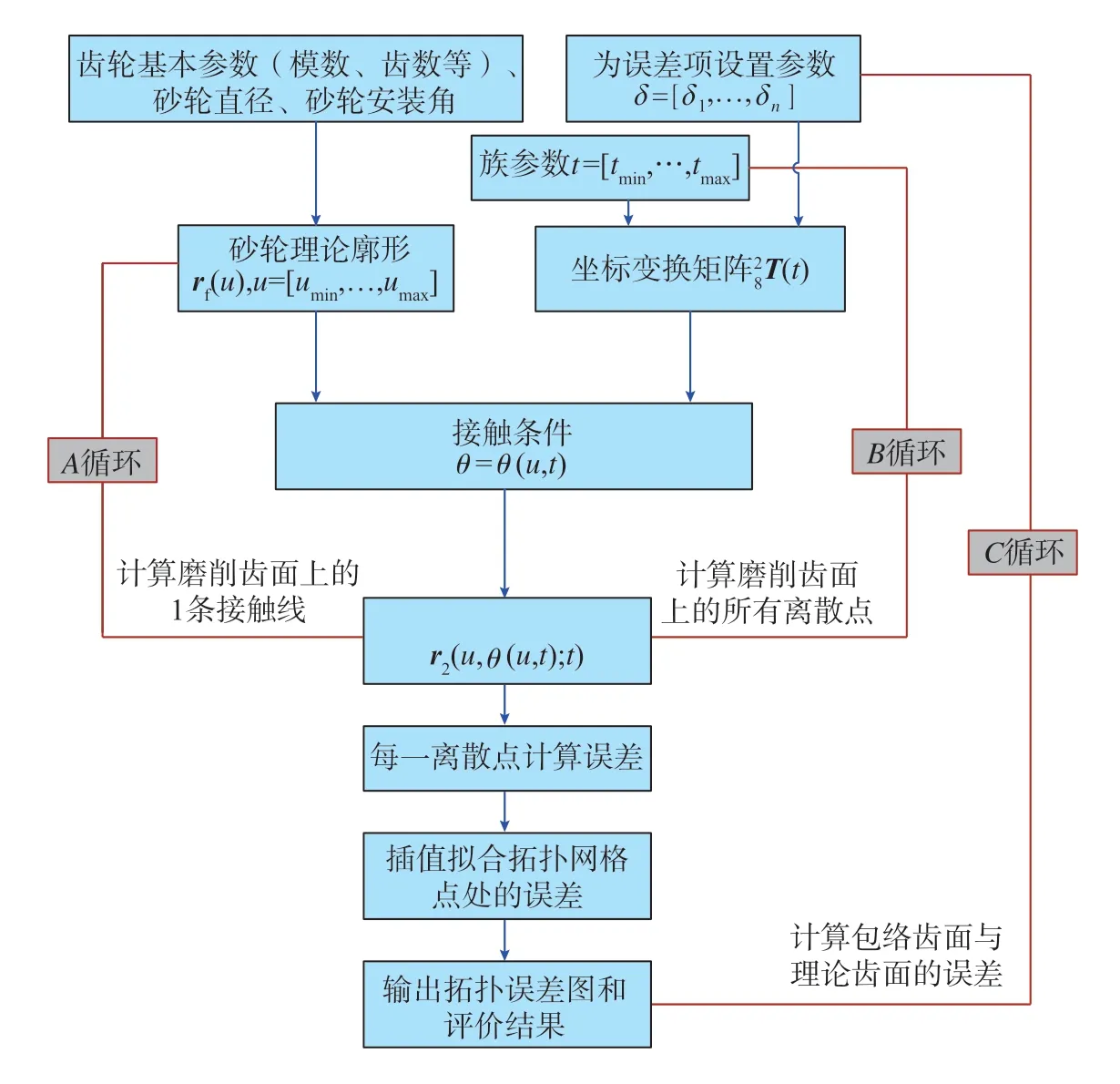
图6 装配几何误差-成形磨削齿面误差评价流程图Fig.6 Assessment flowchart of assembly geometric errors and gear tooth surface errors

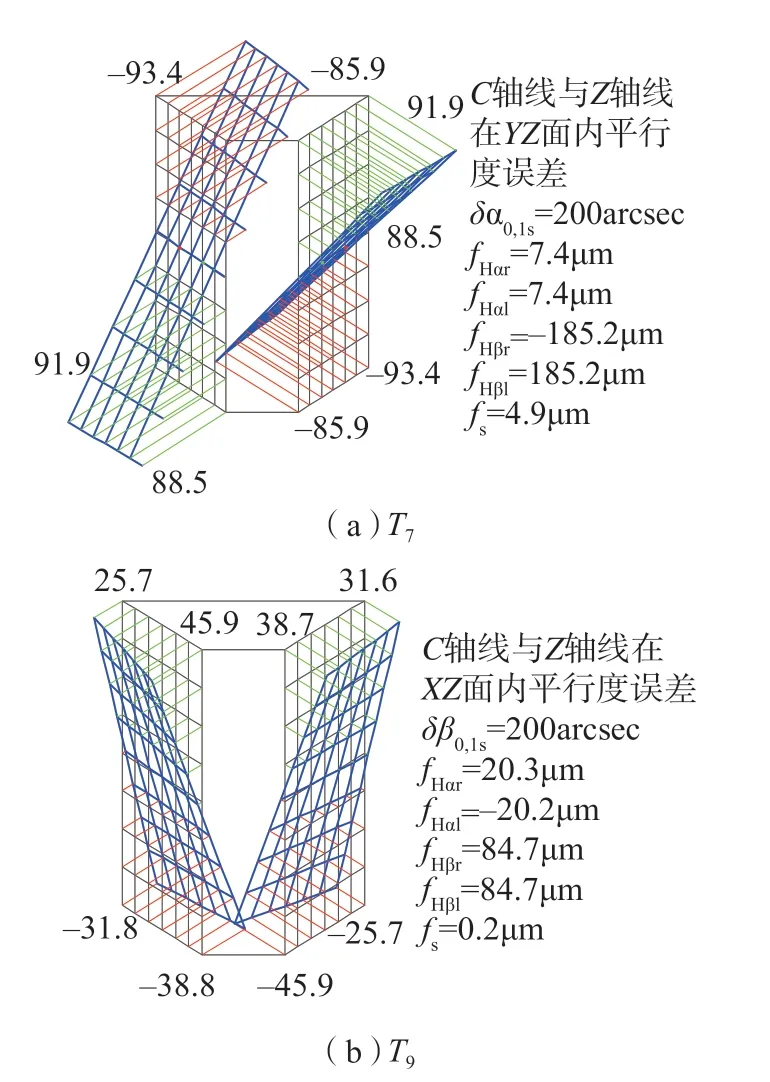
图7 磨削系统装配几何误差项T7和T9产生的齿面拓扑误差Fig.7 Topographical errors of gear tooth surface resulted from assembly geometric errors T7 and T9

进一步分析发现以下6个特点：（1）单个几何误差项产生的磨削齿面误差，在左右齿面上数值大小是相同的，但方向有些相同，有些是相反的； （2）在15个误差项中，如图7所示，只有T7和T9的这两个误差项对螺旋线倾斜偏差有影响，而且影响显著； （3）T1、T2、T3、T5、T6、T8、T11、T13、T14和T15对齿廓倾斜偏差有影响，如图8所示，T1、T3、T6和T8对左右齿面的影响是相同的，如图9所示，T2、T5、T11、T13、T14和T15对左右齿面的影响是相反的； （4）T6为A轴参考点偏移的误差，可以理解为磨齿前砂轮偏摆的角度误差，当该角度误差为200arcsec时，产生的误差大小只有约6μm，而一般该角度误差均＜20arcsec，所以T6对于成形磨齿精度影响较小； （5）如图10所示，T4、T10和T12几乎不会产生任何齿面误差，但是会影响实际加工过程中左右齿面的加工余量，所以实际中也需要控制误差大小； （6）T1对齿厚偏差有显著影响，而其他误差项对齿厚偏差的影响很小。

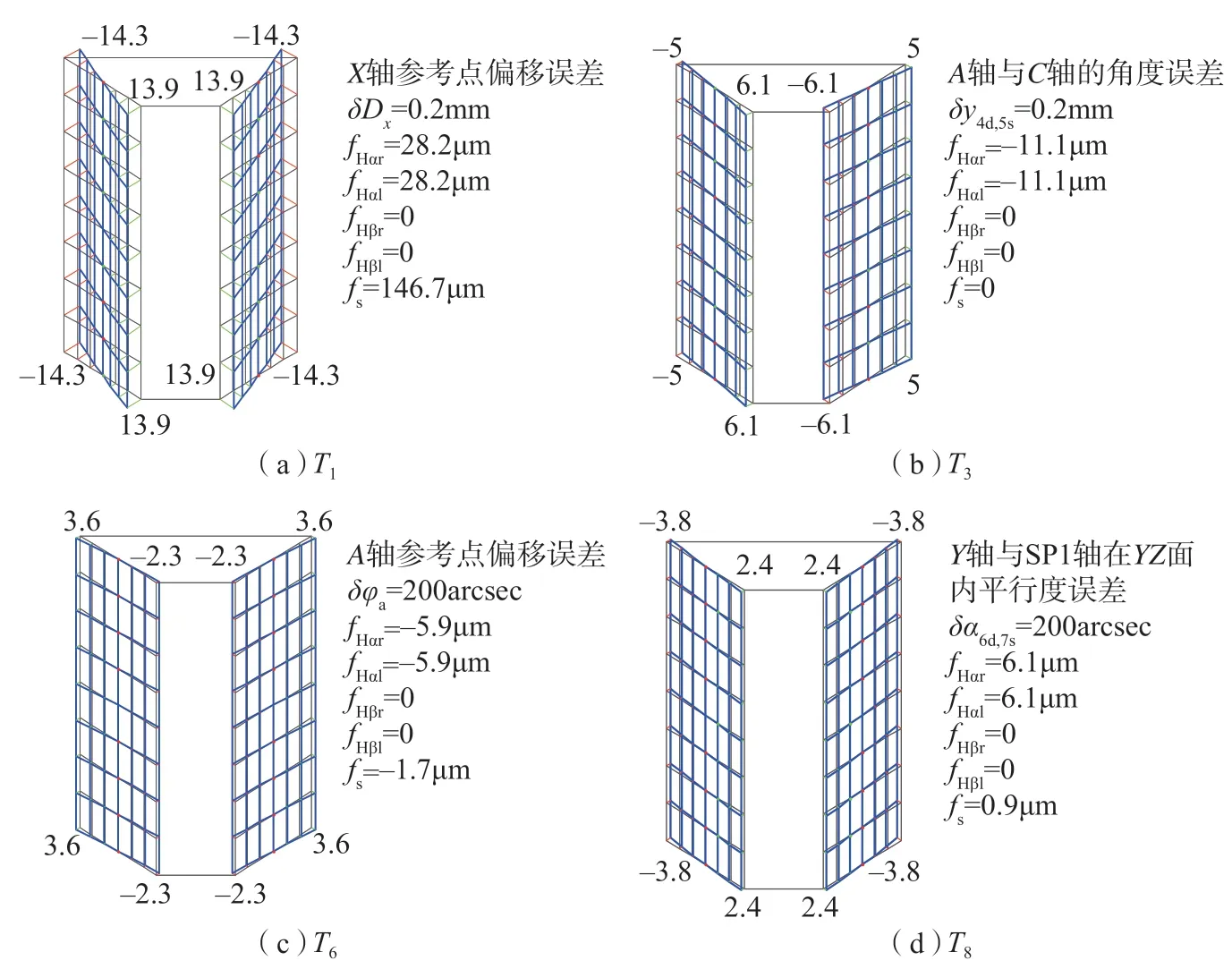
图8 磨削系统装配几何误差项T1、T3、T6和T8产生的齿面拓扑误差Fig.8 Topographical errors of gear tooth surface resulted from assembly geometric errors T1, T3, T6 and T8

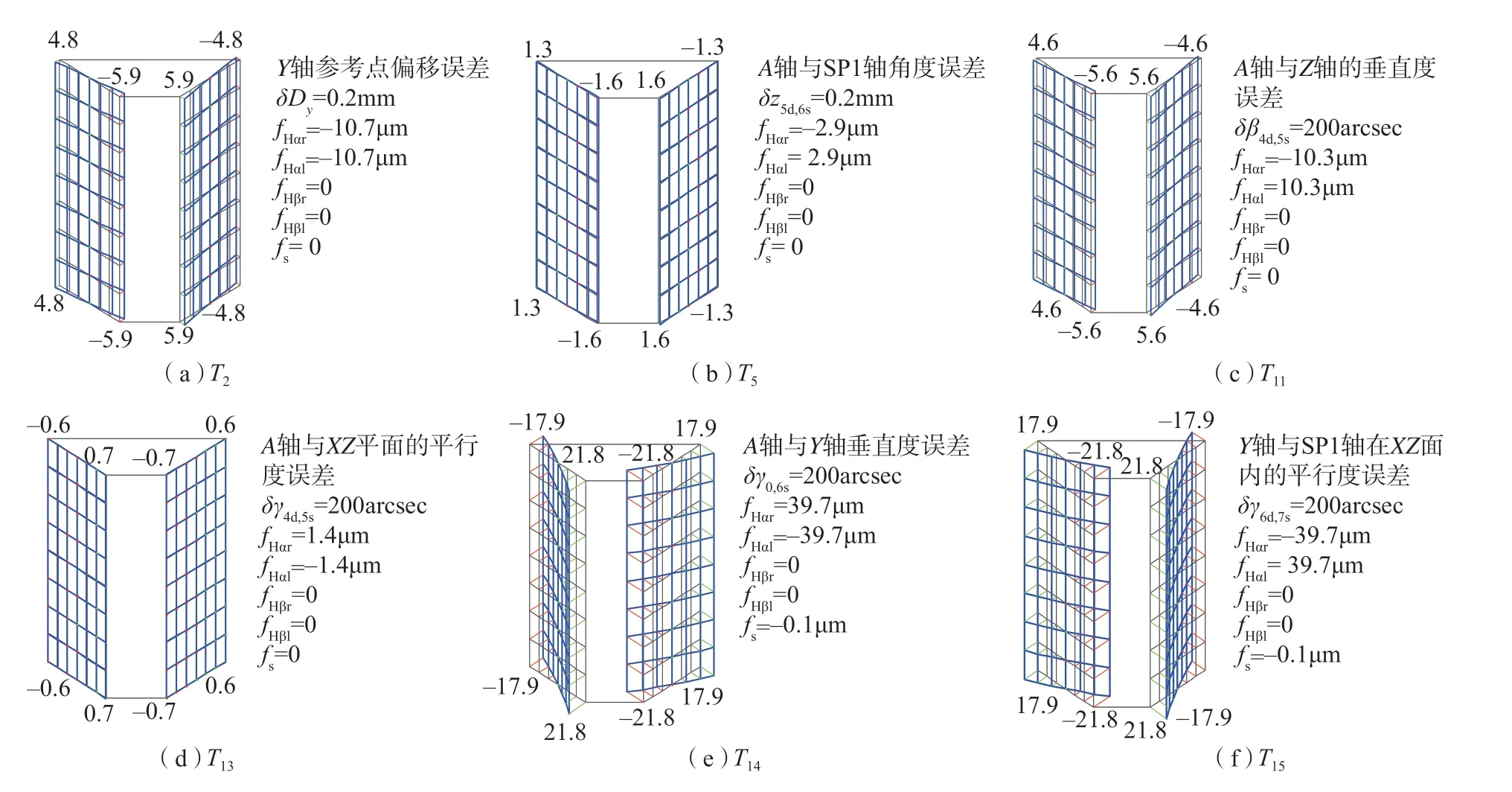
图9 磨削系统装配几何误差项T2、T5、T11、T13、T14和T15产生的齿面拓扑误差Fig.9 Topographical errors of gear tooth surface resulted from assembly geometric errors T2, T5, T11, T13, T14 and T15

3.2 多值计算分析

前述分析可以看出，影响齿厚偏差的为T1；影响齿廓倾斜偏差的为T1、T2、T3、T5、T6、T8、T11、T13、T14和T15；影响螺旋线倾斜偏差的为T7和T9。图11为T1变化时，齿厚误差的变化情况，可以看出T1与齿厚偏差之间呈线性关系。

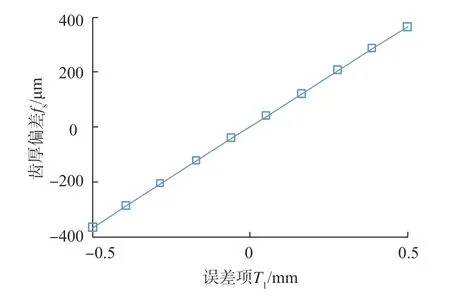
图11 误差项T1与齿厚偏差之间的关系Fig.11 Relationship between tooth thinckness deviations and T1

图12和13分别为直线类误差项T1、T2、T3、T5和角度类误差项T6、T8、T11、T13、T14、T15共10项误差变化时，齿廓倾斜偏差的变化情况，可以看出在规定值范围内，所有这些误差项与齿廓倾斜偏差也呈线性关系，其中T1、T2、T3、T11、T14和T15对齿廓倾斜偏差的影响较大。图14为T7和T9两项误差变化时，螺旋线倾斜偏差的变化情况，也呈线性关系。上述分析结果表明，在研究数值范围内各项误差之间的影响满足线性叠加原理，多个误差项的共同作用使得齿廓倾斜偏差和螺旋线倾斜偏差累计增大。

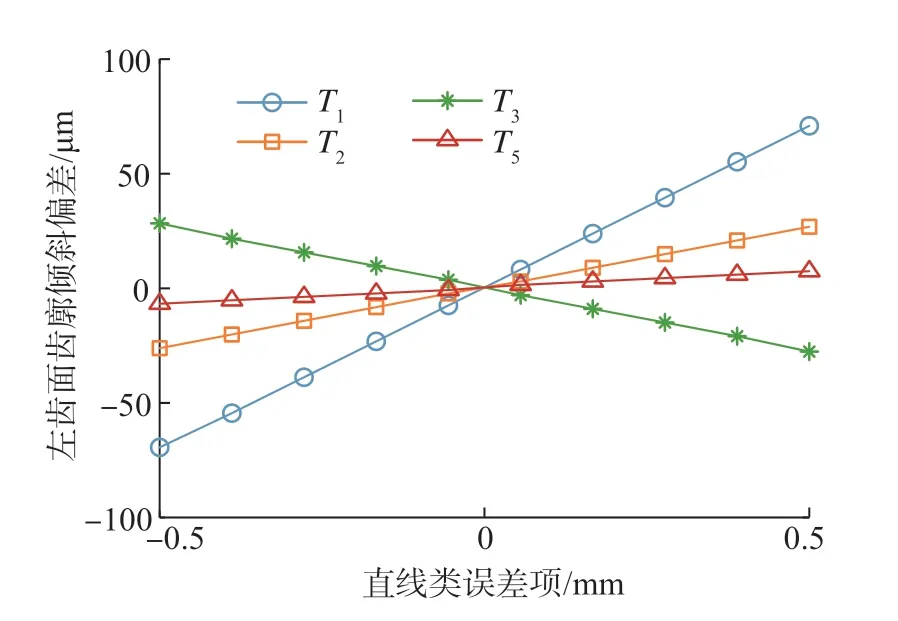
图12 直线类误差项与齿廓倾斜偏差之间的关系Fig.12 Relationship of tooth profile slope deviations and line errors

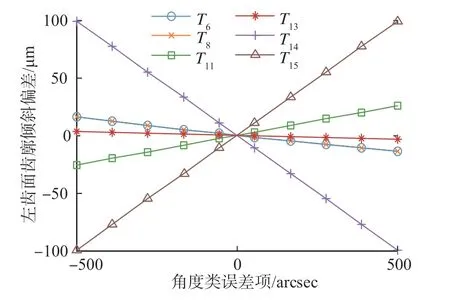
图13 角度类误差项与齿廓倾斜偏差之间的关系Fig.13 Relationship of tooth profile slope deviations and angle errors

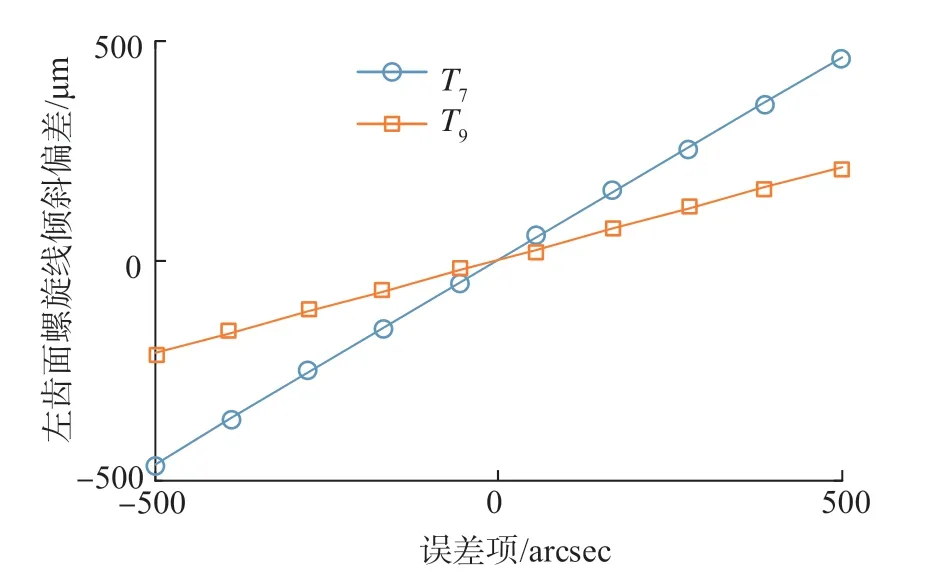
图14 误差项T7和T9与螺旋线倾斜偏差之间的关系Fig.14 Relationship of spiral slope deviations and T7 and T9

3.3 装配精度调整及成形磨齿试验

根据以上分析结果，按照GB4级的齿面精度要求，优化分配了SKMC-1200W/08数控成形磨齿机床的15项装配几何误差允许值，如表3所示。并在调整到位后的数控成形磨齿机床上进行了齿轮成形磨削试验，磨齿的基本参数如表2所示，磨削过程如图15所示。齿轮精磨到尺寸后，在Wenzel三坐标测量仪上进行精度测量，齿廓和螺旋线的检验报告整理后如表4所示，齿廓和螺旋线精度均达到GB4级，满足预期精度设计要求。

图15 SKMC-1200W/08数控成形磨齿机床磨削过程Fig.15 Grinding process of SKMC-1200W/08 gear profile grinding machine

表3 磨削系统装配几何误差允许值Table 3 Allowable assembly errors of profile grinding system

表4 齿廓和螺旋线偏差测量结果Table 4 Measurement results of tooth profile deviations and spiral deviations

4 结论

基于曲面族包络理论，建立了包含磨削系统装配几何误差的成形磨削齿面模型，提出了实现磨削齿面误差评价的流程方法，分析了各装配几何误差对成形磨削齿面误差的影响。根据分析结果和齿轮齿面精度的要求，优化分配了各装配几何误差，并进行了机床装配精度调整和齿轮成形磨削试验。

（1）15项装配几何误差中，T1、T2、T3、T5、T6、T8、T11、T13、T14和T15影响齿廓倾斜偏差，其中T1、T3、T6和T8对左右齿面的影响是同向对称的，其他对左右齿面的影响是反向对称的；T7和T9主要影响螺旋线偏差，其中T7对左右齿面的影响是反向对称的，T9对左右齿面的影响是同向对称的；T1对齿厚偏差有显著影响；T4、T10和T12对磨削齿面误差影响很小。

（2）在研究的误差范围内，当磨削系统的装配几何误差项数值变化时，导致相应的齿廓倾斜偏差和螺旋线倾斜偏差均呈线性变化，各项误差之间的影响满足线性叠加原理；研究结果应用于大型数控成形磨齿机床的装配精度调整，齿轮成形磨削试验结果表明，在数控成形磨齿机床的精度设计中，利用该方法可以指导优化分配各装配误差。