基于经验模态分解法的下穿铁路工程对既有轨道变形监测数据降噪方法
2022-07-15潘兴良刘建国
潘兴良 刘建国
(1.中铁七局集团有限公司, 450016, 郑州; 2.同济大学道路与交通工程教育部重点实验室, 201804, 上海;3.上海轨道交通结构耐久与系统安全重点实验室, 201804, 上海∥第一作者, 正高级工程师)
1 经验模态分解法概述
近年来,随着我国铁路交通网的迅速发展,城市轨道交通下穿铁路工程施工愈加频繁,不限速、长距离、大跨度地安全下穿铁路是未来施工的发展方向。这需要下穿铁路工程在进行合理设计与施工的同时,加强对既有铁路轨道结构变形的实时、高精度监测,及时反映施工情况,达到信息化施工的目的,从而最大程度地控制下穿铁路工程中既有轨道的变形[1]。然而,在对下穿铁路工程中的既有轨道结构进行变形监测时,除了由监测设备本身以及各类环境因素影响而产生测量误差外,其监测对象如既有轨道结构自身还会因环境温度变化而发生变形[2],这些因素会掩盖由下穿铁路工程施工所引起的既有轨道结构的真实附加变形,影响对现场施工实际情况的判别。因此,根据各类影响因素引起的既有轨道结构监测数据的变化特征,有针对性地对监测数据进行降噪,尽可能地还原下穿铁路工程施工引起的既有轨道结构附加变形,有待作进一步的深入研究。
将既有铁路轨道结构测点的变形监测数据视为1组时间序列,其主要由测量误差成分、温度变形成分和下穿施工引起的附加变形成分构成,且具有非平稳性、非线性的变化特征。对于时间序列中的信号成分提取问题,常用的方法主要有低通滤波法[3]、小波分析法[4]和EMD(经验模态分解)法[5]等。
在采用低通滤波法时,首先需要通过傅里叶变换将时间序列转换至频域上进行分析;然后利用下穿铁路工程施工引起的附加变形成分相较于测量误差成分及温度变形成分具有的变化周期最长的特点,运用低通滤波法提取附加变形成分,但运用时必须选择合适的滤波器参数和截止频率,否则会因参数选择的不合理导致附加变形成分过少被提取或提取的附加变形成分掺杂过多的干扰信息。此外,虽傅里叶变换能够完成信号的时、频域转换,但不能同时具有二者信息。因此,该方法仅适用于平稳信号的处理,并不太适用于处理非平稳信号。
小波分析法通过傅里叶变换,将时域上无限长的正弦波函数转换成能量在时域上十分集中的小波方式,解决了傅里叶变换不能同时反映时频信息的问题。但运用小波分析法处理具体信号时,同样需要对小波基、分解层数和去噪方式等进行选择,不合理的参数选择会影响信号的降噪效果。文献[6-7]于1998年提出了希尔伯特-黄变换(以下简为“Hilbert变换”)方法。该方法由EMD法及对应的Hilbert变换构成:首先,通过EMD法,根据信号自身的时间尺度特征将原始信号自适应地分解得到数个IMF(内蕴模态函数),并通过对每个IMF作相应的Hilbert变换,从而获得其随时间变化的瞬时频率与瞬时幅值,即Hilbert时频谱;然后,将Hilbert时频谱在时间上进行积分,可求得Hilbert边际谱,而Hilbert边际谱能够反映对应的IMF的各个瞬时频率的总幅值大小,这是IMF的重要表征函数;最后,利用各阶IMF的Hilbert边际谱特征,将周期变化趋势相近的若干阶IMF叠加,重构周期趋势成分,实现对原始信号中各成分的提取。EMD法从信号的瞬时频率出发,是局部的、自适应的信号成分分离方法,同时适合处理非平稳、非线性的信号。
本文利用EMD法分离下穿铁路工程中既有铁路轨道结构变形监测数据的组成成分,剔除轨道结构变形监测数据中的干扰因素信号,实现该工程中对既有铁路轨道结构变形监测数据的降噪与分析。
2 EMD法的计算原理
任何非平稳、非线性的复杂信号都是由一些不同的IMF构成,且任意两阶的IMF相互独立。
其中,IMF是单分量信号,这就需要其满足下列条件:① 对于整个数据集,IMF上的极值点及过零点的数目必须相等或最多相差1个;② 在任意时刻,由局部极大值点所构成的上包络线和局部极小值点所构成的下包络线的平均值为零,即上包络线和下包络线相对于时间轴而言是局部对称的。
基于上述假设,可以在无需先验证基函数的情况下,根据信号自身时间尺度特征,自适应地将多分量复杂信号分解成多阶内蕴模态函数及余项之和。
(1)
式中:
t——信号采集对应的时间;
ci(t)——IMF分量;
rm(t)——余量;
x(t)——信号幅值。
这种筛分过程能够根据原始信号自身特征,将信号中不同的频率成分按照高频至低频的顺序,分解成符合单变量信号特征的各阶IMF,余项则是原始信号中的趋势项。
利用EMD法从原始信号中分解出的各阶IMF及趋势项不一定具有明确的物理含义。但根据各阶IMF时间尺度上的变化特征,将周期趋势相近的IMF进行叠加,可重构出具有明确物理含义的各周期趋势成分。
由式(2)—式(7)可计算得到各阶IMF的Hilbert幅值谱及边际谱。确定其在频域上的频率分布特征,便于实现对各阶IMF进行分类与组合。
(2)
(3)
(4)
(5)
(6)

(7)
式中:
τ——积分变量;
T——自然数序列;
j——虚数;

a(t)——瞬时幅值;
θ(t)——相位函数;
ω(t)——瞬时频率;
H(t,ω)——Hilbert幅值谱;
h(ω)——Hilbert边际谱。
此外,对于离散的数字信号而言,Hilbert边际谱可由式(8)—式(9)求得:
h(nΔω)=∑kH(tk,nΔω)
(8)
tk=kΔt
(9)
式中:
n——离散的频率间隔,k,n∈Z;
k——离散的时间间隔,k,n∈Z;
h(nΔw)——离散数字信号Hilbert边际谱;
tk——离散时刻;
H(tk,nΔw)——对应于tk的Hilbert幅值谱;
Δω——频率分辨率;
Δt——采样时间间隔。
3 某地铁盾构隧道下穿铁路工程仿真算例
本文采用在某地铁盾构隧道下穿既有铁路工程中,盾构推进至既有铁路影响范围之前的监测数据中添加附加变形模拟数据的方式,构建仿真信号。为贴近工程实际,附加变形模拟数据考虑了既有铁路轨道结构变形控制较为理想(第1类)、不够理想(第2类),以及在发生较大附加变形后采取适当措施使其部分恢复(第3类)的3类典型工况。3类仿真信号如图1所示。
以第1类仿真信号为例,经EMD法分解得到的各阶IMF如图2所示。
由图2可看到,各阶IMF的周期趋势特征大体上以日周期变化为界,分为3类;而各类IMF的叠加分别对应测量误差成分、温度变形成分和附加变形成分。为了进一步明确3类成分所含有的IMF,计算各阶IMF的Hilbert边际谱。为了避免边际谱幅值的影响,将上述边际谱量纲一化,如图3所示。

a) 第1类仿真信号

b) 第2类仿真信号

c) 第3类仿真信号图1 3类仿真信号Fig.1 Three types of simulation signals
由图3可看到,随着IMF的阶数升高,各阶IMF的Hilbert边际谱频率峰值逐渐变小。仿真信号中高频部分主要集中在第1阶IMF,反映了测量误差成分;中频部分主要集中在第2~4阶IMF,反映了温度变形成分;低频部分主要集中在第5~6阶IMF及余项,反映了附加变形成分。

图2 第1类仿真信号经EMD法分离得到的各阶IMFFig.2 IMF of the first type of simulated signals obtained by EMD separation

图3 仿真信号的各阶IMF量纲一化后的Hilbert边际谱Fig.3 Hilbert marginal spectrum of normalized IMF of simulated signals
对各阶IMF归类叠加之后,分离出的3类信号成分如图4所示。
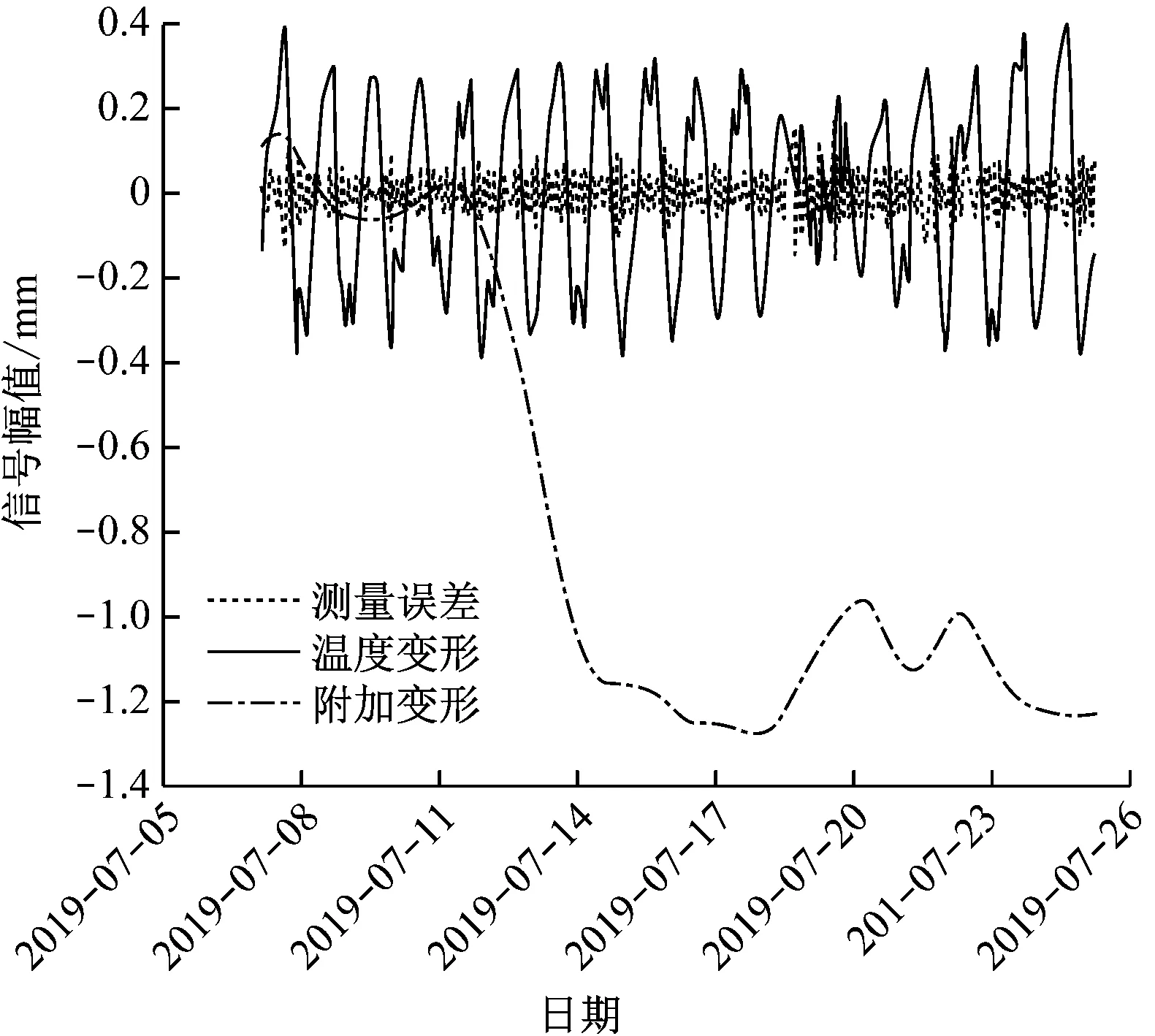
图4 第1类仿真信号中3类信号成分提取结果
从3类信号成分提取结果中可看到,3类信号成分得到了有效分离。其中,测量误差成分集中在±0.05 mm左右;温度变形成分有明显的周期变化趋势,其变化幅值约为±0.3 mm/d,附加变形成分变化趋势与事先添加的附加变形模拟数据基本一致。3类仿真信号附加变形成份提取结果评价见表1。
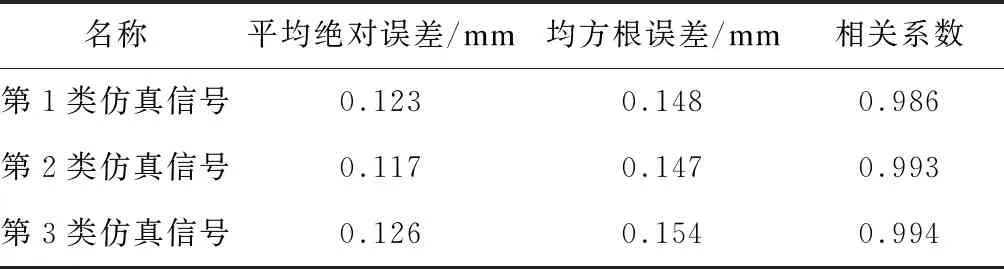
表1 3类仿真信号附加变形成份提取结果评价
4 某地铁盾构隧道下穿铁路工程实测数据分析
为验证降噪效果,选取某地铁盾构工程下穿既有铁路车站工程的轨道结构变形监测数据进行分析。该地铁盾构工程下穿了客货共线铁路、快速铁路及高速铁路。其中,客货共线铁路为非电气化铁路,采用有砟道床、混凝土轨枕,设计速度为120 km/h;快速铁路为Ⅰ级双线,采用有砟道床、混凝土轨枕,设计速度为200 km/h;高速铁路采用有砟道床、混凝土轨枕,设计速度为250 km/h,线下预留350 km/h的提速条件。监测仪器采用徕卡TM30型全站仪,该型仪器角度的监测精度为0.5″,距离的监测精度为0.2 mm+0.4×10-6L(L为距离)。
高速铁路轨道结构某测点沉降监测数据,如图5所示。
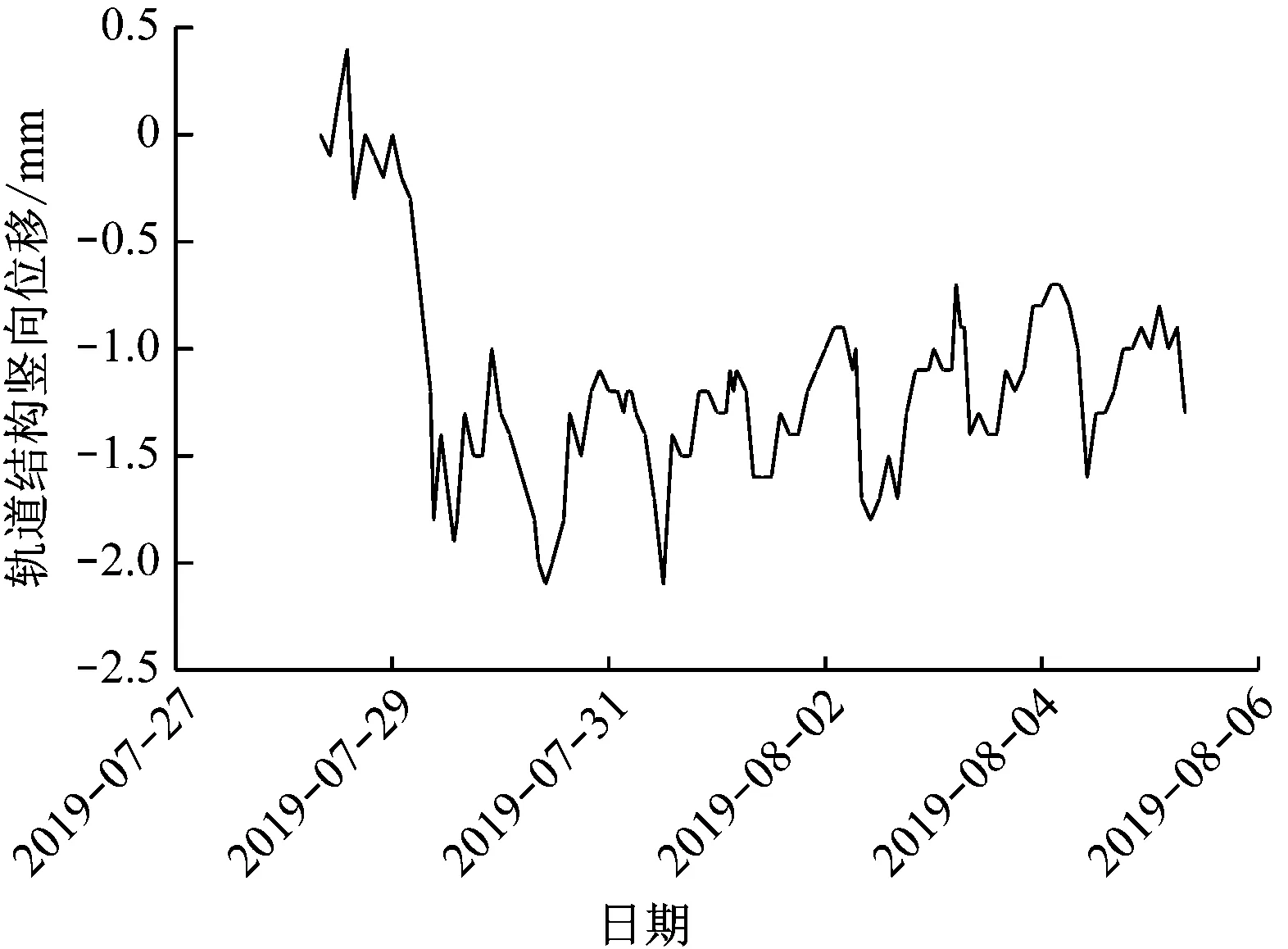
图5 高速铁路轨道结构变形实测数据Fig.5 Measured data of track structure deformation of high-speed railway
由图5可看到,高速铁路轨道结构变形监测数据中除了由盾构下穿引起的线路沉降以外,还明显包含呈周期变化趋势的轨道结构温度变形成分及测量误差成分。通过EMD法分解上述实测数据得到各阶IMF,以及对应的量纲一化后Hilbert边际谱,如图6~7所示。

图6 高速铁路轨道结构实测数据分解出的各阶IMFFig.6 Decomposition of IMF from measured data of high-speed railway track structure

图7 实测数据的各阶IMF量纲一化后的Hilbert边际谱Fig.7 Hilbert marginal spectrum of normalized IMF of measured data
同样地,将各阶IMF的Hilbert边际谱按照频率的集中范围分成高频、中频、低频3组,分别对应3类信号成分。具体地,第1阶IMF对应测量误差成分;第2、3阶IMF对应温度变形成分;第4阶IMF及其余项对应附加变形成分。实测数据的3类信号成分提取结果如图8所示。
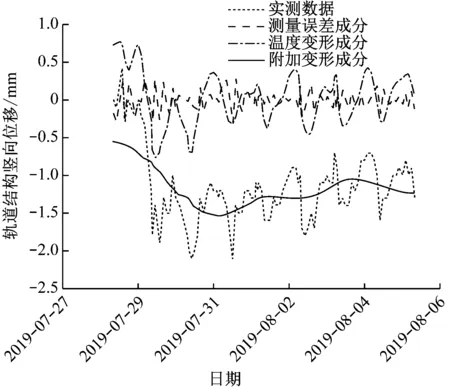
图8 高速铁路轨道结构实测数据中各信号成分提取结果
从实测数据中3类信号成分提取结果可看到,3类信号在时间序列端点处的数值存在明显的失真现象。例如,温度变形成分周期性变化幅值达到了近1.5 mm,同时附加变形成分在下穿盾构还未对线路产生影响时,轨道结构就已产生了0.5 mm左右的沉降,这显然都不符合实际情况。产生此类情况的主要原因在于EMD法中常见的“端点效应”。
由于基于EMD法构建的信号上、下包络线是通过局部极值点得到的,这就导致除非待处理的信号端点正好为局部极值点,否则获得的信号上、下包络线在端点处无法取得精确值而产生拟合误差;且随着迭代过程的进行,该误差始终存在,其影响区域还会从端点处向信号内部扩散,最终“污染”整条信号,这就是所谓的端点效应。
为了克服端点效应,文献[7]提出了特征波延拓法,但并未给出具体解释。在后续针对EMD法的研究中,国内外众多学者都提出了很多延拓方法,大致研究方向主要集中在神经网络延拓[8]、镜像延拓[9-10]和自回归模型延拓[11-12]等。
本文从实测数据变化特点及快速有效的角度出发,选取了镜像闭合延拓的方法。根据信号端点的分布特性,选择适合的对称位置对实测数据信号两端进行延拓,使得实际的端点数据不在待处理信号的端点上,避免产生端点效应。
经过镜像闭合延拓处理之后的实际监测数据分解出的3类信号如图9所示。由图9可看到,在端点处3类信号都得到了有效收敛,抑制了端点效应,提高了EMD法的分解精度。
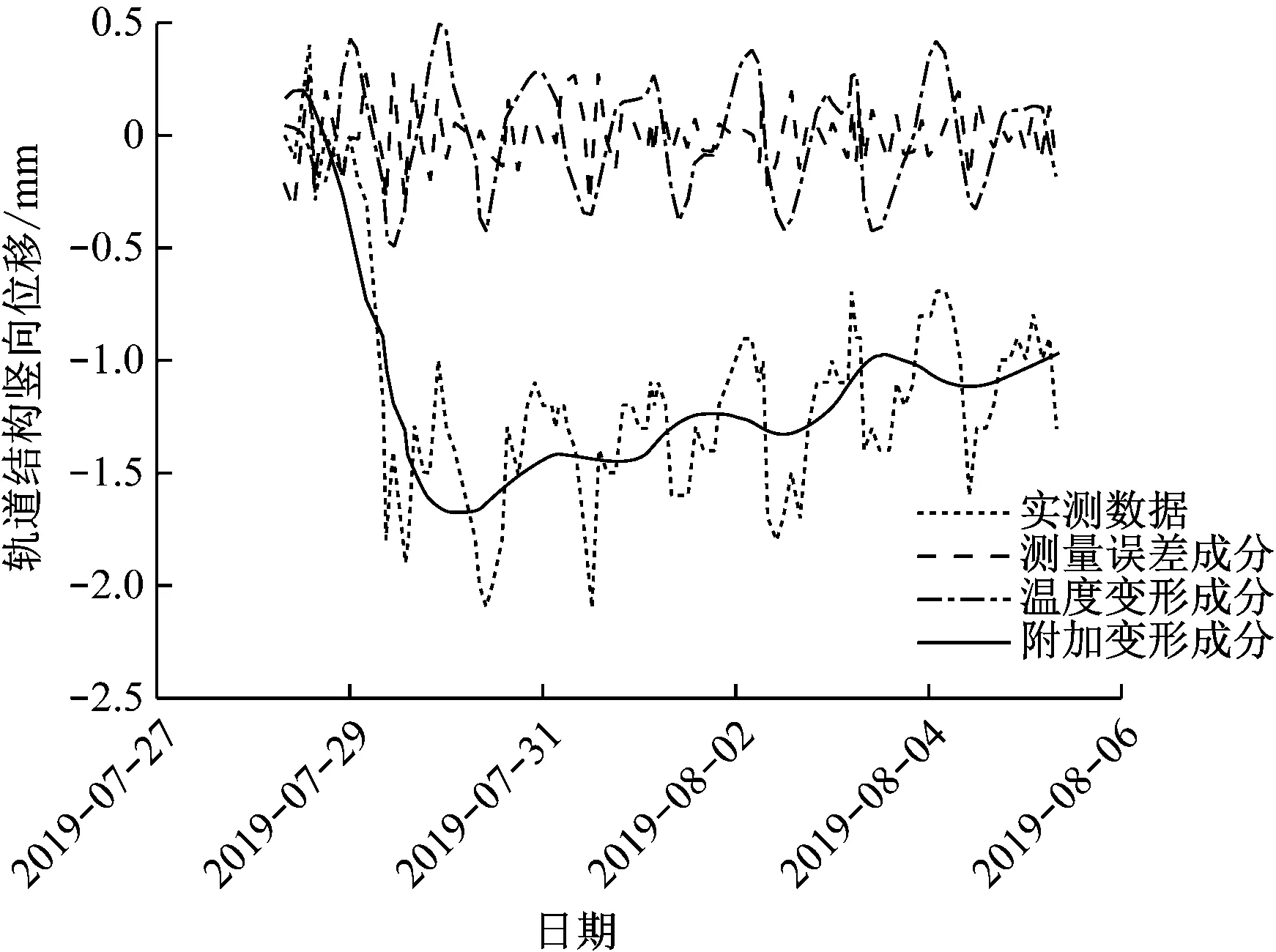
图9 镜像闭合延拓后实测数据各信号成分提取结果
5 结论
1) EMD法能够实现对测量误差、环境温度引起的轨道结构竖向变形,以及邻近铁路工程施工引起的轨道结构附加变形等3类信号成分的有效分离。在3类典型工况下,运用该方法所提取的轨道结构附加变形成分与附加变形模拟信号之间的平均绝对误差在0.1 mm左右。
2) 利用EMD法提取的附加变形成分存在 “端点效应”,即在端点处存在数据发散的失真现象,难以真实反映工程实际情况。利用镜像闭合延拓方法可以有效消除端点效应,实现了对下穿铁路工程轨道变形监测数据的有效降噪。
