城市轨道交通车站站台门抗冲击性能的研究*

2022-07-15吴爱中闭永雷曾骁晹金启华

城市轨道交通研究 2022年6期

吴爱中闭永雷曾骁晹金启华

(1. 上海工程技术大学城市轨道交通学院, 201620, 上海； 2. 上海地铁第一运营有限公司, 200003, 上海；3. 上海市特种设备监督检验技术研究院, 200062, 上海∥第一作者，讲师)

为了实现安全防护功能，城市轨道交通车站站台门应当具有足够的强度。站台门可能承受的载荷包括：隧道活塞风压(正压或负压)，人群挤压和不理智乘客的冲撞等。这些载荷的单独作用或叠加作用会造成站台门结构的弹性或塑性变形。其中，塑性变形会导致结构的破坏，所以应当竭力避免；而弹性变形过大也可能会侵犯地铁限界条件[1]，因此需要对其进行强度验算。相对于风压和人群挤压这样的静态加载而言，站台门玻璃面板受动态冲击载荷时更为脆弱。这是因为站台门玻璃面板是一种脆性材料，受到过大的冲击载荷会导致面板碎裂。

城市轨道交通车站站台门大多采用单片钢化玻璃作为面板材料。钢化玻璃任意局部受到破坏时，整块玻璃会迅速破碎成颗粒。虽然钢化玻璃具有良好的力学性能(其强度是普通玻璃的3～5倍[2])，但站台门玻璃面板碎裂的例子并不罕见。

城市轨道交通站台门玻璃面板的破裂重则危及乘客安全和车辆安全，轻则影响轨道交通的运行秩序，从而造成不良影响。因此，站台门抗冲击性能的研究具有重要的现实意义和学术价值。文献[3]采用有限元方法进行了站台门结构分析，得到了站台门关键部件的变形及应力分布。文献[4]基于ANSYS软件对站台门钢化玻璃面板的承载特性进行了分析，讨论了玻璃面板厚度、开槽尺寸和圆角等参数对玻璃面板应力分布的影响。文献[5]采用数值方法对固定门受到风压、人群挤压及冲击等载荷叠加作用时的变形进行了计算。上述研究工作主要集中在站台门结构的静强度分析，而站台门抗冲击的理论和试验研究鲜有报道。

本文采用试验样机检测与有限元模拟相结合的方法，对站台门的抗冲击性能进行了研究，重点考察了固定门玻璃面板受到乘客冲击的载荷。首先介绍了站台门的摆锤冲击试验方法和装置；然后建立了摆锤冲击的有限元模型，重点分析了摆锤冲击作用下站台门玻璃面板的受力和变形情况，并将不同模型的分析结果与测试结果进行比较；最后建立摆锤冲击扩展有限元模型，初步分析玻璃面板受到重载冲击的破裂行为。

1 站台门摆锤冲击试验方法与装置

城市轨道交通车站站台门的摆锤冲击试验通常在试验样机上进行[1]。典型的站台门样机包括1个固定门、1个应急门、1个滑动门，以及相应的驱动和控制系统。考虑到固定门玻璃面板的尺寸比应急门和滑动门玻璃面板的尺寸大，更容易产生变形和破坏，因此摆锤冲击试验主要针对固定门进行。目前，国内外都有专门针对玻璃面板材料的摆锤冲击测试标准[6-8]，譬如EN 12600—2002非常具体地规定了摆锤冲击测试方法和试验装置(见图1)。EN 12600—2002推荐的试验装置包括支撑框架、冲击体和悬挂部件等核心组件，需特别注意，该标准规定的冲击体为充气轮胎。

GB 15763.3—2009《建筑用安全玻璃》亦详细规定了摆锤冲击试验方法和装置(见图2)。该规范要求采用的玻璃支撑框架和摆锤悬挂方式应与EN 12600—2002的要求大体上相同。但与EN 12600—2002明显不同的是，GB 15763.3—2009规定的冲击体是1个霰弹袋，其袋体面料为皮革，袋内填充物是公称直径小于2.5 mm的铅砂。皮革袋的中心轴设计了1根金属杆，起固定和支承作用，同时连接φ3 mm的悬挂钢丝绳。为了使摆锤束紧充实且经久耐用，铅砂袋外部采用玻璃纤维增强聚酯尼龙帯卷缠起来，整个摆锤的质量为(45.0±0.1)kg。

注：h0为摆锤的冲击(下落)高度。

考虑到充气轮胎摆锤冲击玻璃门后的回弹比较大，容易形成多次冲击，因此操作不方便，而铅砂袋摆锤冲击玻璃门体后的回弹相对较小。同时从冲击体硬度而言，人体肌肉组织与充气轮胎差别较大，而与铅砂填充的皮革袋更为接近，因此选择铅砂袋摆锤作为冲击体。试验时，将摆锤悬挂在固定门上方的梁上，摆锤冲击点为固定门站台侧玻璃面板的中心。参照产品制造商的要求，从2 mm逐步增大到700 mm。为了测量玻璃门体受摆锤冲击后产生的位移，在固定门玻璃门体的轨道侧对应于冲击点的位置装设了位移传感器(型号为PM11-R1-30L，精度为0.001 mm)。级联信号调理器和数值显示设备，可以记录和显示玻璃门体冲击处的最大位移。

2 站台门摆锤冲击数值模拟分析

2.1 站台门摆锤冲击模型的建立

由于站台门钢化玻璃的造价较高，破坏性试验成本较大，同时受试验条件限制，部分试验载荷不容易达成。因此，为了进行比较和拓展，开展了站台门摆锤冲击试验的数值模拟工作。本文采用ABAQUS有限元软件对固定门的摆锤冲击过程进行了有限元建模和非线性分析。由于固定门的几何外形、载荷及边界条件具有对称性，取1/4实体进行建模计算，建立的模型包括钢化玻璃、圆形摆锤及金属框架3个部分。模型中，玻璃与金属框架之间设置为完全黏结的约束方式，而玻璃与摆锤之间设置为接触相互作用。其中，玻璃与摆锤的接触属性包括法向硬接触和切向库伦摩擦接触(摩擦系数设置为0.1[10])。模型中，金属框架和摆锤采用三维八节点六面体单元(C3D8)，玻璃面板采用壳单元和三维实体单元。考虑到固定门玻璃面板的厚度(10 mm)远小于其长度(2 480 mm)和高度(2 100 mm)，因此采用壳单元能够很好地反映玻璃面板变形情况，而且其变形量相对实体单元模型而言更小。为在后续研究中应用一些经典的基于实体单元的断裂分析手段，需重点关注三维实体单元模型。站台门摆锤冲击有限元模型见图3。

a) 实体单元3部件模型

b) 壳单元3部件模型

c) 实体单元2部件模型

d) 壳单元2部件模型

e) 采用实体单元玻璃面板的摆锤自由坠落冲击模型

f) 采用壳单元玻璃面板的摆锤自由坠落冲击模型图3 站台门摆锤冲击有限元模型Fig.3 Finite element models for platform screen door pendulum impact

图3 a)和3 b)分别为采用三维实体单元和壳单元的玻璃门体有限元模型。其中，壳单元模型共有78 501个单元，83 172个节点；而三维实体单元模型共有93 573个单元，97 136个节点。在上述两种模型中，金属框架、玻璃面板和摆锤的材料参数完全相同，具体见表1。由于铅砂袋摆锤的材料组成非常复杂，使用弹性模量、泊松比等力学参数对摆锤的材料力学性质进行描述并不准确。因此在本文模型中，尝试采用一种黏弹性材料的广义Maxwell材料模型对其进行模拟[9-10]。有限元模型中，金属框架底面被完全固定，选择在冲击体的对称面上施加相应的载荷，包括冲击初速度和冲击力。轨道交通站台门的招标技术文件中，针对站台门冲击载荷的常见规定是：冲击力为2 800 N，冲击时间为0.08 s，作用面积为0.01。分析了不同加载条件下玻璃面板的变形(有限元模型见图3 c)和3 d))。采用ABAQUS/Standard程序对站台门摆锤冲击有限元模型进行静态分析，输出冲击力和玻璃面板冲击点位移；采用隐式动力学算法，分析摆锤从处自由坠落而后冲击玻璃门体引起的变形(有限元模型见图3 e)和3 f))。采用隐式积分算法求解固定门撞击过程的瞬时动力学响应时，先计算节点加速度，然后对其积分得到节点速度，而后对速度积分得出节点位移，最后可算出应变、应力、反力等数值结果。隐式积分算法基于向后差分格式对控制方程进行时间积分运算，具有无条件稳定的优点。

为了模拟玻璃面板破裂行为，使用XFEM (扩展有限元方法) 对站台门摆锤冲击过程进行数值分析。XFEM增添了带有不连续性质的形函数来代表单元内的间断，不需设置精细网格也能够捕捉裂纹的扩展行为，是模拟不连续问题(譬如裂纹)的新方法。其最大优点是不需在实体内部的几何物理界面上划分网格，从而克服了传统有限元在裂纹尖端高应力区域必须细化网格所带来的困难。

在扩展有限元模型中，将整块玻璃面板考虑为可能破裂的区域，但不限定裂纹的初始位置、数量和扩展路径，而是通过设定断裂准则来判定材料起裂位置和裂纹扩展路径。具体而言，玻璃面板的初始状态是完整的，无初始裂纹缺陷。随着加载的进行，玻璃面板的应力、应变状态不断发展，采用最大主应力判据和能量释放率准则来确定起裂位置和裂纹扩展路径，通过适时计算单元积分点的最大主应力判断单元是否达到断裂条件。扩展有限元法无需在裂纹尖端区域设置精细网格，且基于ABAQUS/Standard的隐式分析具有较高的精度，较为适合于玻璃面板的断裂分析[9]。但实际模拟中依然会面临很多挑战，常常会遇到数值收敛困难，特别是模拟玻璃面板从局部起裂，到整片玻璃面板完全碎裂成颗粒的全动态过程目前具有很大难度。因此，除了采用一些通用的促进数值收敛的技巧外，本文还采用了一些针对性措施：对于那些满足断裂失效条件的单元，保留其承受压力载荷的能力，限制其承受剪切及拉伸载荷的能力，同时标记失效单元在网格中的存在。这些处理方法已被成功用于研究金属板材受圆柱体弹丸高速冲击所导致的剪切带破坏问题[11]，藉此模型初步讨论玻璃面板受摆锤冲击可能出现的破裂问题。

表1 站台门摆锤冲击有限元模型材料参数

2.2 站台门摆锤冲击模拟结果对比分析

为了校核模型的准确性，比较了玻璃面板变形量随摆锤冲击力变化曲线，见图4。对于三维实体单元模型，图4 a)显示了玻璃面板厚度方向实体单元数量分别为2、4和6时的变形量。由图4 a)可见，玻璃面板厚度方向单元的数量对三维实体单元模型的结果有一定影响；当玻璃面板厚度方向单元数量为2时，其变形量明显偏小；而当玻璃面板厚度方向单元数量为4时，其冲击力-变形量曲线与单元数量为6的模型结果趋于一致。图4 b)给出了不同建模方法时的玻璃面板变形量随摆锤冲击力变化曲线。由图6 b)可见，采用三维实体单元的3部件模型(包括玻璃面板、摆锤和金属框架)和2部件模型(包括玻璃面板和金属框架)计算得出的玻璃面板变形量随摆锤冲击力变化曲线几乎完全一致；而采用壳单元的3部件模型与2部件模型计算得出的结果具有一定差异，但在考察范围(冲击力2 800 N)内，其差值不超过10%。采用壳单元2部件模型的突出优点是计算量小，因为不需要进行复杂的非线性接触运算，因此适合于站台门玻璃面板的静强度校核。

a) 不同玻璃面板单元类型及数量

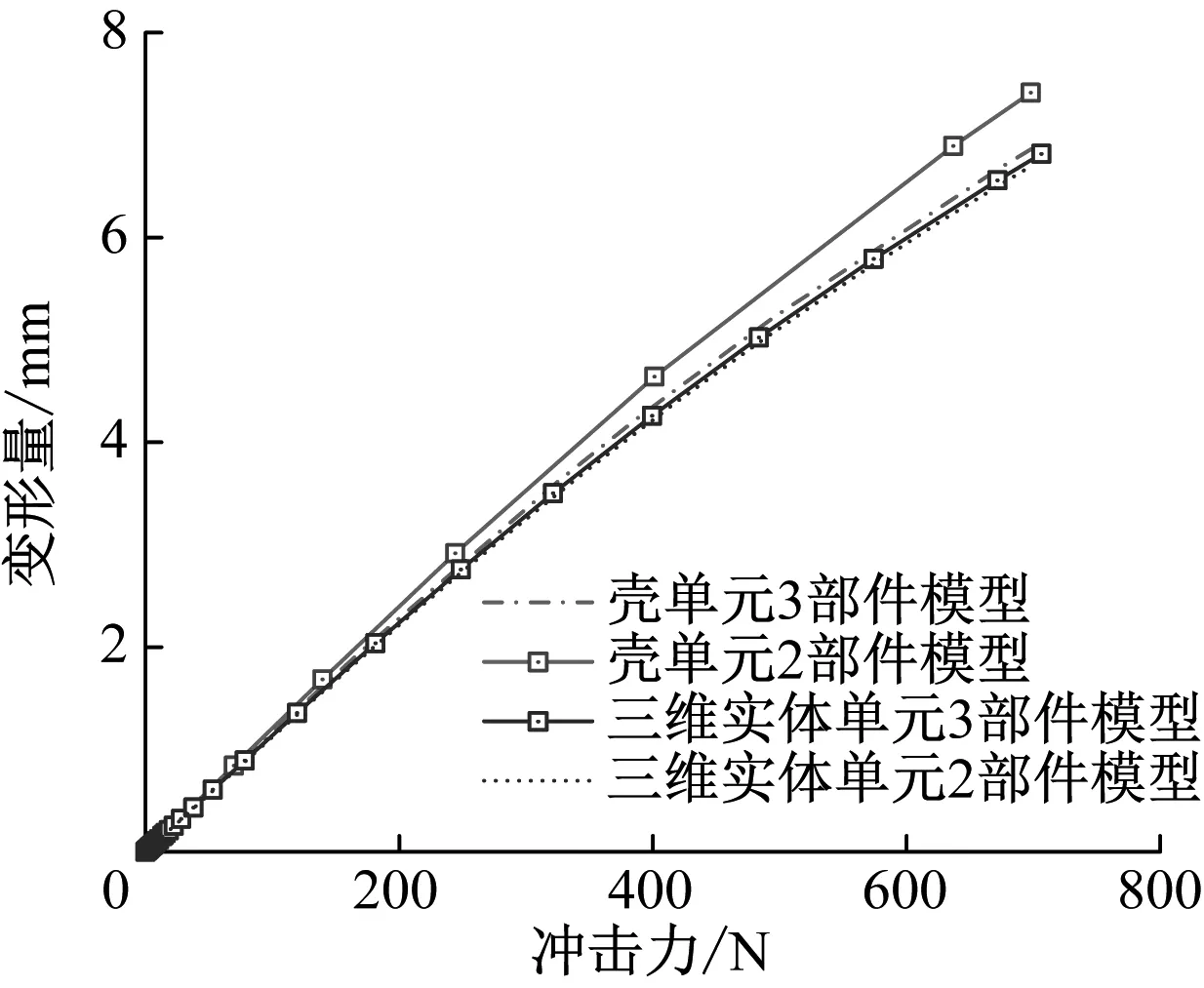
b) 不同加载模型图4 玻璃面板变形量随摆锤冲击力变化曲线Fig.4 Curve of glass panel deformation changing with pendulum impact force

国内大多数城市轨道交通线路中，站台门玻璃面板采用单片的钢化玻璃，显然玻璃面板厚度对于其承载变形特性有直接影响。采用壳单元模型，并验算玻璃面板厚度对其冲击力-变形量曲线的影响，见图5。由图5可见，在冲击力相同的条件下，分析结果符合玻璃面板越厚、变形量越小的规律。当玻璃面板厚度为12 mm时，其冲击力-变形量的关系曲线近似为1条直线；而当玻璃面板厚度为6 mm时，其冲击力-变形量的关系曲线具有上凸幂函数图像的特征。针对检测条件，当玻璃面板厚度为10 mm时，考虑冲击力2 800 N、作用面积0.01 m2的加载情况，玻璃面板的变形量约为7 mm。

图5 玻璃面板变形量随摆锤冲击力变化曲线

基于图3 e)和3 f)所示模型的动力学分析结果，图6给出了不同冲击高度时，玻璃面板冲击点的变形量，并给出了其实测结果与有限元计算结果。由图6可见，玻璃面板变形量的实测结果与有限元计算结果大体上比较接近，其较大差值出现在前2次冲击中，相对误差最大值达到了23%。产生该误差的原因是，图6显示的有限元计算结果为玻璃面板的变形量，而玻璃面板变形量实测值除了其自身变形量以外，还包括门体构件(门框或立柱)的位置变动。由于构件连接(譬如长圆孔螺栓连接)处通常存在间隙，承载时，这些机械连接部位存在一定的位移，因此，玻璃面板的变形量实测结果大于有限元计算结果是合理的。当玻璃面板进行多次冲击后，这些机械间隙逐渐趋于稳定，因此后几次玻璃面板变形量的实测结果与有限元计算结果更加相符。实际检测发现，当冲击高度在200～700 mm范围内，即冲击初速度在1.98～3.70 m/s范围内时，在试验现场可以听到巨大的撞击声，但站台门结构和玻璃面板未发生破坏。

图6 玻璃面板变形量随摆锤冲击高度变化曲线Fig.6 Curve of glass panel deformation changing with pendulum falling height

基于三维实体单元的玻璃面板扩展有限元模型，分析了冲击高度分别为1 200 mm和1 500 mm，对应的冲击初速度分别为4.85 m/s和5.42 m/s时的冲击情况，见图7。由图7可见，通过动态分析得到的玻璃面板冲击力-变形量曲线表现出局部弯折的丰富细节，这些特征与静态分析所得的曲线有显著的差别。这可能是由摆锤动态冲击时应力波在玻璃面板中传播过程中遇到边界发生反射等复杂动力学效应引起的，其中深层次的确定性原因还有待于更进一步探究。当冲击高度为1 500 mm时，玻璃面板在其加载历程的末尾阶段发生了局部单元破损的情况，其标志是单元的损伤耗散能大于0，见图7。此外，考察了专门表征玻璃面板单元损伤的状态变量。图8显示了玻璃面板最先出现破损的单元。分析发现，在玻璃面板冲击点的背面(即玻璃面板轨道侧)最先萌生裂纹，因为该位置受到拉应力，而玻璃面板的冲击面受到的是压应力。这些细节基本符合脆性断裂的特点。然而必须指出：采用扩展有限元方法虽能模拟玻璃面板受重载冲击萌生裂纹的情况，但目前还不能再现整片玻璃面板完全碎裂成颗粒的全过程；甚至也不能很好地模拟玻璃面板脆裂的放射形裂纹形态和周向裂纹扩展行为[12]，除非在玻璃面板中预先设置径向和周向的初始裂纹[9](这种办法限制了起裂位置和裂纹扩展路径，具有相当的局限)。后续将采用内聚力单元模型和显式动力学方法[13-15]，研究站台门玻璃面板受冲击破裂的裂纹扩展行为。