基于遗传算法-BP神经网络的动车组列车轮对磨耗模型*

高明亮 邵俊捷 常振臣 王连富 刘德权 牛振虎 陈之恒

(1. 中车长春轨道客车股份有限公司检修研发部， 130062, 长春；2. 西南交通大学牵引动力国家重点实验室， 610031， 成都∥第一作者， 高级工程师)

轮对是动车组走行部的核心部件之一。准确预测轮对的磨耗，可以提前安排镟修计划，并做出精准镟修决策，从而延长轮对的使用寿命，保证列车的运行安全。因此，建立一个精准、高效的轮对磨耗预测模型很有必要。本文构建了相关性算法-GA算法(遗传算法)-BP神经网络预测模型，对轮对磨耗的历史数据进行了相关性分析。提取影响轮对磨耗的两个主要参数:轮径磨耗,轮缘厚度磨耗，并将其作为BP神经网络的输入参数。同时采用GA算法优化BP神经网络，对轮径磨耗、轮缘厚磨耗两个参数进行拟合。

1 基于相关性算法的轮对磨耗影响因素分析

动车组轮对从运行开始，磨耗便伴随其整个服役周期直至报废。由于不同条件下轮对磨耗速率有很大差别，故确定轮对磨耗的影响参数是准确预测轮对磨耗的前提。针对各参数间关联形式的不确定性，结合线性、非线性相关算法计算相关系数，并提取相关性强的影响参数，得到训练模型的样本集。

Pearson系数rp的计算公式如下：

(1)

式中：

yi、bi——分别为两个相关参数的实际数值；

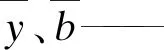
n——样本数量。

rp的取值范围为[-1,1]。若|rp|越靠近1，表明轮对磨耗与该检测参数的线性相关性越高。

Spearman算法是一种非线性相关系数的计算方法。Spearman系数rs的计算公式如下：

(2)

式中：

mi、si——分别为两个相关参数的实际数值；

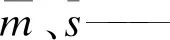
根据两种算法计算出rp、rs，并分别给予其对应的权重p、q。本次p取0.6，q取0.4。则：

rab=prp+qrs

(3)

式中：

rab——总相关系数。

以某路局某型动车组列车为例，整理出近500条轮对磨耗数据。选取车厢号、轴号、间隔天数、轮径值、轮缘厚度、轮径差、轮缘厚度差等影响因素做相关性分析。根据式(1)—式(3)，计算相关系数,见表1。

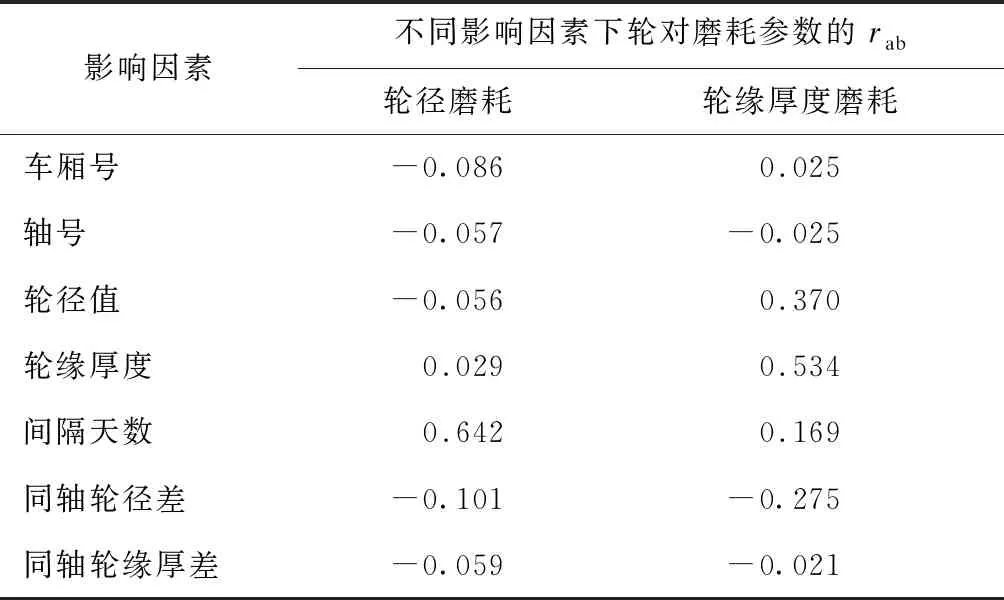
表1 某型动车组列车轮对磨耗相关性分析结果

由表1可见，对轮对磨耗的影响由大到小依次是：间隔天数，轮缘厚度，轮径值，同轴轮径差，车厢号，轴号，同轴轮缘厚度差。其中，间隔天数对轮径磨耗、轮缘厚度磨耗的影响最大，此处的间隔天数可近似当作“里程”。偏相关系数反映了两个变量间的净相关程度，在控制了轮径值、轮缘厚度的线性影响后，轮缘厚差与轮缘厚磨耗之间的偏相关系数为-0.14，有较大相关性。结合车厢号、轴号的特殊性，选取间隔天数、轮径值、轮缘厚度、轮径差、轮缘厚度差5个因素作为BP神经网络的输入参数。

2 BP神经网络模型结构的确定

如图1所示，BP神经网络模型结构由3层构成，即1个输入层、1个隐含层和1个输出层，n、m、o分别为输入层、隐含层和输出层的层数。其中，输入层和输出层不变，隐含层的层数可以根据模型要求而调整。设输入X=[X1,X2,…,Xn]，输出Y=[Y1,Y1,…,Y1],隐含层个数为m。

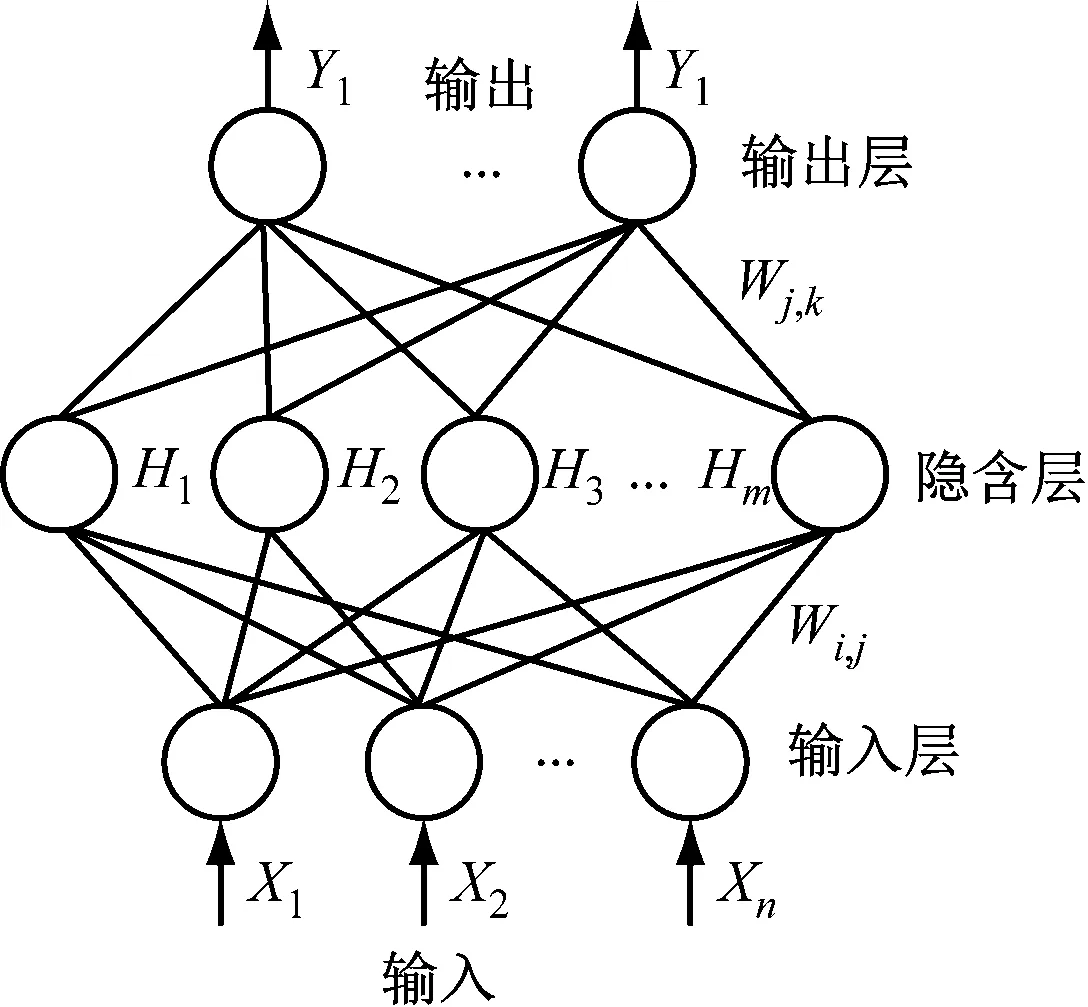
注：Wi,j为输入层与隐含层之间的连接权值； Wj,k为隐含层层与输出层之间的连接权值； Hm为第m个隐含层的输出值； m为隐含层的节点个数。

该模型的训练原理如下：随机设置连接权值W，以及隐含层、输出层的阈值γj、θk,然后进行隐含层的输出计算。计算公式为:

Hj=f(αj-γj)

(4)

其中:

(5)

式中：

Hj——第j个隐含层的输出值；

γj——第j个隐含层的阈值；

f——隐含层激励函数；

αj——第j个隐含层的输入。

输出层输出Yk的计算公式为：

Yk=g(βk-Θk)

(6)

其中:

(7)

式中：

g——输出层激励函数；

Θk——第k个输出层的阈值；

βk——第k个输出层的输入；

l——输出层的节点个数。

由网络预测输出Y和期望输出O，计算均方误差Ek：

(8)

任意参数νi的更新估计式为：

νi+1=νi+Δνi

(9)

BP神经网络算法基于梯度下降策略，以目标的负梯度方向对权值和阈值进行调整。根据计算出的均方误差Ek，设定学习速率η。Wj,k的调整方法为：

(10)

(11)

同理可得:

(12)

(13)

输出层阈值的更新方法为：

(14)

(15)

根据上述算法对权值、阈值进行迭代调整。若迭代算法结束，则输出相关结果；若迭代算法未结束，则返回重复该训练过程。

3 BP神经网络优化步骤

采用遗传算法来优化BP神经网络，即采用遗传算法优化BP神经网络的初始权值和阈值。实现步骤如下：

1) 整理数据。对数据进行预处理，并确定BP神经网络的输入、输出变量。

2) 确定BP神经网络的基本模型。确定BP神经网络的各层层数，并初始化其权值和阈值。

3) 初始化种群和构建适应度函数。确定各权值和阈值的个数，给每个个体进行编码。适应度函数的计算公式如式(14)：

(16)

式中：

n——预测数据量；

Oi——输出参数实际值；

Yi——输出参数预测值；

F——个体适应度。

根据式(16)计算出初始种群每个个体的适应度值。

4) 种群的选择、交叉与变异。随机选择个体的概率与其适应度函数值成反比，遗传算法选择轮盘赌法；交叉是为了将上一代优秀基因组合遗传至下一代，随机选取两个个体的1个基因位置作为交叉位置，组成新的优秀个体：

(17)

式中：

Aj0、Bj0——两个个体；

j0——基因位置；

e——[0,1]内的随机数。

则变异参数f(g0)为:

f(g0)=[r(1-g0/G)]2

(18)

若p>0.5，则第i个个体j0位置的基因数值ai,j,n+1为:

ai，j,n+1=ai,j,n+(ai,j,n-amax)f(g0)

(19)

若p<0.5，则：

ai，j,n+1=ai,j,n+(amin-ai,j,n)f(g0)

(20)

式中：

r——随机数；

g0——已进化代数；

G——总进化代数;

amax——基因上界；

amin——基因下界。

5) 完成参数优化。当遗传算法迭代次数且预测结果满足期望误差值时，输出最优个体。

6) 构建BP神经网络。将通过遗传算法优化后的初始权重和阈值分配给BP神经网络，进行训练和预测。

4 GA-BP神经网络模型训练及结果分析

以某路局某型动车组列车为例，共得到485条试验数据，将前400条数据用于训练，剩余85条数据用于检测。设置GA-BP神经网络的结构为5-12-2，即5个输入层、12个隐含层、2个输出层。其中，输入层中的5个参数分别为间隔天数、轮径值、轮缘厚度、轮径差、轮缘厚度差，输出层的2个参数分别为轮径磨耗、轮缘厚度磨耗。模型共有84个权值、14个阈值。GA-BP神经网络隐含层激励函数选用tansig，输出层激励函数选用purelin，训练函数选用traingd(梯度下降法)，学习率为0.01，最小目标值误差为0.1。种群数目为20，进化代数为30，交叉概率为0.2，变异概率为0.1。要求轮径值磨耗预测误差在0.5 mm之内，轮缘厚度磨耗误差在0.1 mm之内。

对GA-BP神经网络进行训练、预测。由图2可见，大部分轮径值磨耗预测误差小于0.5 mm，大部分轮缘厚度磨耗预测误差小于0.1 mm，基本满足了精度要求；轮径磨耗预测误差稍大于轮缘厚度磨耗预测误差。

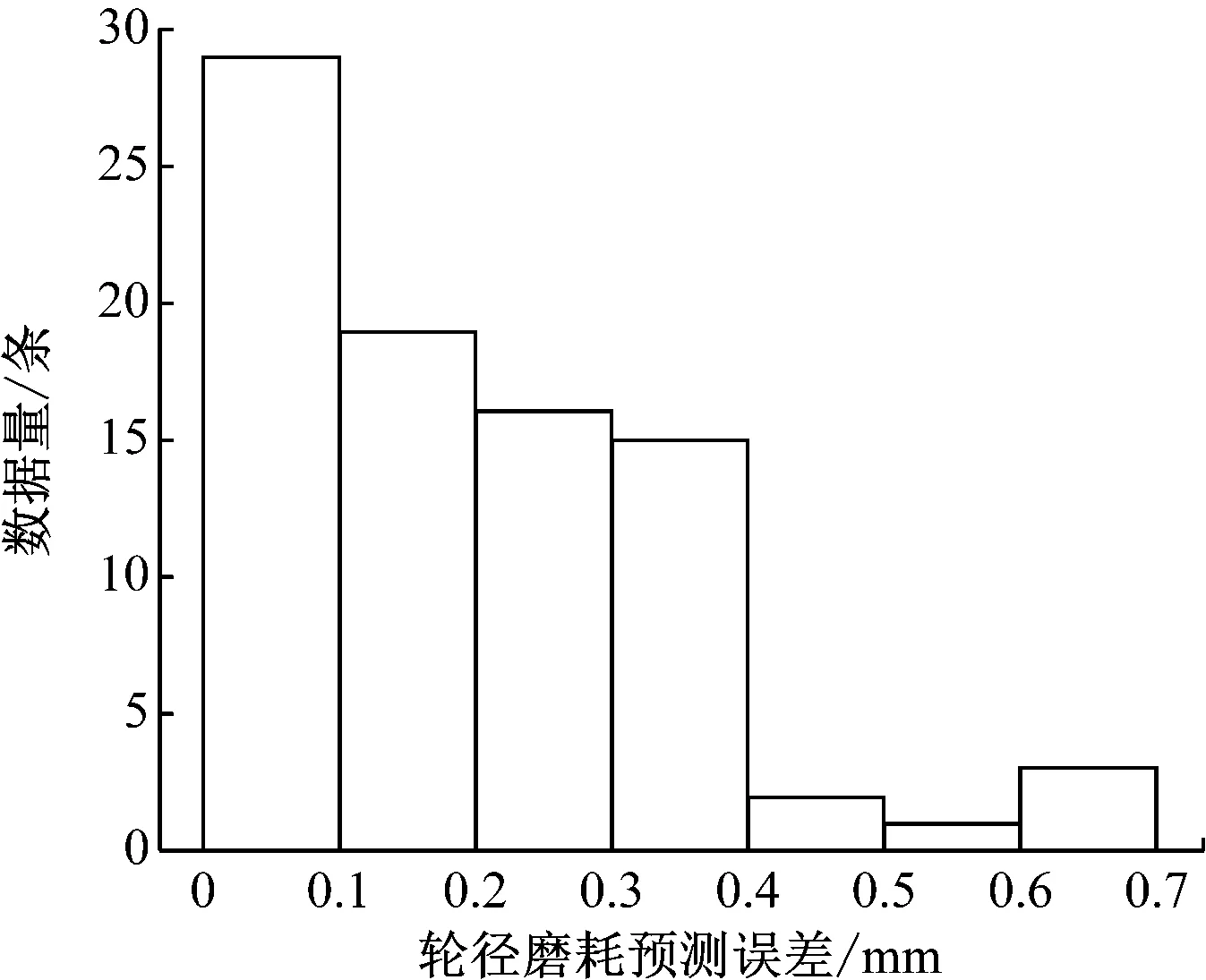
a) 轮径磨耗

图3为GA-BP神经网络预测模型中遗传算法迭代30次的适应度变化图。由图3可见，随着遗传算法的优化，该模型的误差显著降低；在进行17次迭代时，适应度降低至最小值，此时的BP神经网络参数即为模型的最优参数。

为验证遗传算法对BP神经网络的优化作用，选取BP神经网络模型的预测结果与其作比较。根据预测的准确率和平均误差来评估预测效果。对于预测数据，当其误差满足精度要求时，认为此预测数据是准确的(即轮径磨耗预测误差在0.5 mm之内，轮缘厚度磨耗误差在0.1 mm之内)；反之，当误差不满足精度要求时，认为其预测是不准确的。具体结果见表2。

由表3可见，在采用遗传算法对BP神经网络进行优化前，BP神经网络的轮径值、轮缘厚度预测准确率分别为82.73%、76.88%，轮缘厚度预测的准确率偏低。经优化，轮径磨耗预测的准确率提高到了95.29%(提升了12.56%)；轮缘厚度磨耗预测准确率提升幅度更大，达到了91.76%；预测平均误差亦有明显提高。

由此可见，将遗传算法引入BP神经网络有明显的优化作用。通过对比轮对磨耗模型中的轮径值和轮缘厚度可以发现，无论是传统BP神经网络模型还是优化后的GA-BP神经网络模型，其轮径磨耗预测的准确性总是高于轮缘厚度磨耗。这一方面是由于模型对轮缘厚度磨耗预测误差的要求更高；另一方面是由于影响轮缘厚度磨耗的因素很多，导致轮缘厚度磨耗预测的不确定性较大。

5 结语

为对动车组列车运行中的轮对磨耗做出更好的预测，本文利用相关性算法分析确定了轮对磨耗的影响因素；引入BP神经网络算法，并应用GA算法优化BP神经网络的初始权值和阈值，从而构造出GA-BP神经网络模型。利用历史数据对模型进行训练，最终训练好的模型在对轮对轮径磨耗、轮缘厚度磨耗的预测中展现了较好的预测能力，满足了精度需求，证明了GA-BP神经网络模型用于轮对磨耗的预测是可行的。