挠性板弯折的数值分析方法
2022-07-15任桃桃白俊磊王一波
胡 亮 李 欢 任桃桃 白俊磊 王一波
(上海航天控制技术研究所,上海 201109)
0 引言
现阶段航空航天领域产品轻量化、小型化、集成化的趋势愈来愈明显,这对电路印制板结构、尺寸和可靠性的要求越来越高。刚挠结合印制板将传统PCB 板与尺寸更小、安装方式更加灵活的挠性板结合在一起,不仅提高了电子系统连接的可靠性,还使得结构设计方式更加简单、可靠[1-2]。挠性板作为刚挠结合印制板的中间连接部件,制造工艺决定了其自身的刚度、强度等力学性质[3-4],然而在实际使用中挠性板往往存在弯折情况,特别是直角弯折和翻转弯折[5],导致局部应力过大进而造成其失效。挠性板的长度设计需为弯折预留足够的操作空间,还应使弯折到位后板内的应力尽量小,特别是挠性板与PCB板连接处,以及挠性板弯折曲率最大处[6]。
利用有限元分析软件可以方便地计算挠性板弯折的位移、变形、应力以及连接处的弯矩、剪力等情况[7-8],但无法系统地给出各力学参数随挠性板长度变化的曲线,不便于在设计之初给出合适的设计参数。
本文以挠性板翻转弯折为例,从材料力学中梁受力弯曲的挠曲线方程出发,利用数值积分方法求得给定弯矩和剪力情况下的挠性板弯折曲线,再以板长和跨度作为约束条件反算弯矩和剪力的取值[9],在取得板长-跨度-弯矩-剪力4 者关系曲线后作进一步的分析。
1 挠性板弯折的受力分析
一种典型的挠性板翻转弯折如图1所示。图中两块PCB 板平行放置,其右侧端面重合,中间由等宽等厚的均匀挠性板连接,挠性板自由弯曲变形。
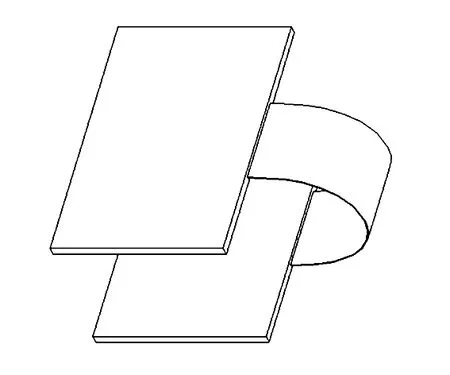
图1 挠性板弯折模型Fig.1 Model of bending flexible plate
挠性板为线弹性变形,采用材料力学中梁弯曲时的中性层假设,认为该层的长度在弯曲时无变化,截面内水平方向应力相同[10],将问题简化为二维受力问题,挠性板的受力情况如图2所示。图中A、B点为挠性板中性层曲线的两端点,C 点为曲线顶点,挠性板在两端点处收到弯矩和剪力的作用,挠性板总长为L,弯折后AB跨度为D,曲线高度为H。
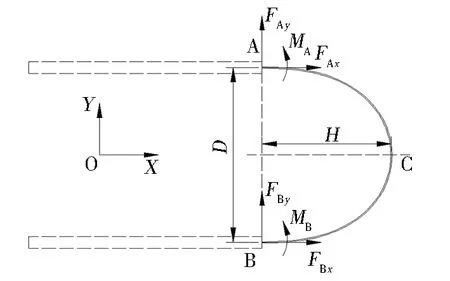
图2 挠性板弯折的受力分析Fig.2 Force analysis of the bending flexible plate
由于挠性板自由变形,其变形具有对称性,且X方向的外力为零。只取上半部分AC 段进行分析,将坐标原点取为A 点,曲线上坐标为X的一点P 的受力如图3所示。
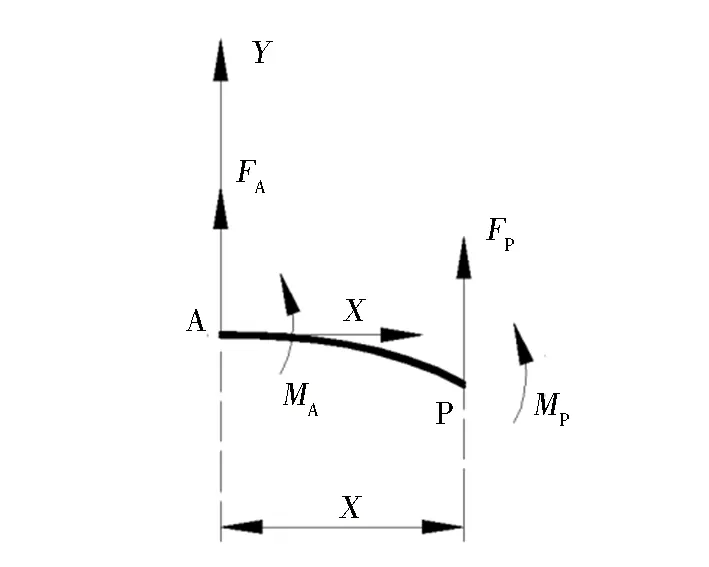
图3 挠性板变形曲线上任意一点的受力分析Fig.3 Force analysis of any point of the bending flexible plate
取力和力矩的正方向与坐标轴正方向相同且满足右手法则,由力和力矩平衡可知:FP=-FA及MP=FAx-MA。即曲线上各点的剪力相同,且力矩为:

2 弯折曲线的数值积分
挠性板视为均一的线弹性材料,同时算例中梁的跨度远大于截面高度,因此根据材料力学中梁的挠曲线方程[10],可得:

式中,E为挠性板材料的弹性模量,I为截面的惯性矩,矩形截面宽度为b,高度为h,则有I=bh3/12。
曲线二阶导数y″与力矩Mx符号相同,根据力矩方向定义,若Mx>0(即力矩为逆时针方向),此时曲线具有上翘(下凸)趋势,对应的二阶导数y″>0。注意到AC 段的末端必然向内弯曲,即斜率为负且迅速减小,可知此处的力矩必然为负值。
将式(1)代入式(2)中,整理得:

已知x0=0,y0=0,y′0=0,上式可用数值积分的方法求取曲线的一阶和二阶导数,进而求得曲线方程。积分方法可选择欧拉法或四阶Runge-Kutta 法[11],后者具有更高的求解精度,且计算量不大,本文选择后者进行求解,递推公式如下:
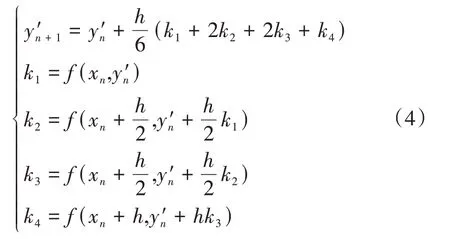
式中,h为步长。坐标y和弧长Δs的递推采用前一点的一阶和二阶导数计算:
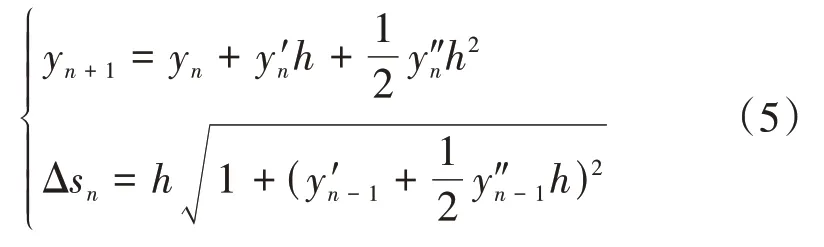
利用MATLAB 软件编写计算程序,考虑到曲线末端斜率增加很快,采用变步长算法来减小计算误差。计算时以终点的斜率作为终止的条件,阈值取为-50 000。积分求解时需确定FA和MA的数值,为方便初值选取,考虑到此时挠性板受纯弯矩作用时其曲率理论上为常数,即弯曲曲线为半径为R的圆弧,则有:1/R=MO/EI,同时取F0=MO/R。挠性板长度为L,则FA和MA的取值定义为:
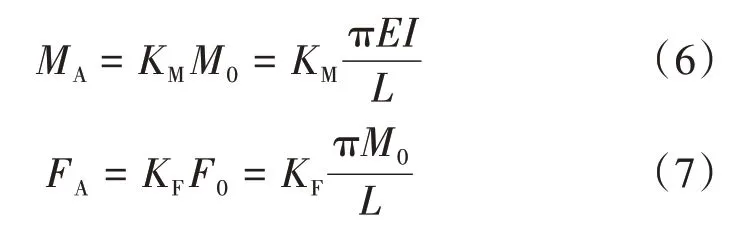
式中,KM和KF分别为力矩和力取值的系数。
MATLAB 中数值计算流程图如图4所示,仿真计算所采用的参数见表1。
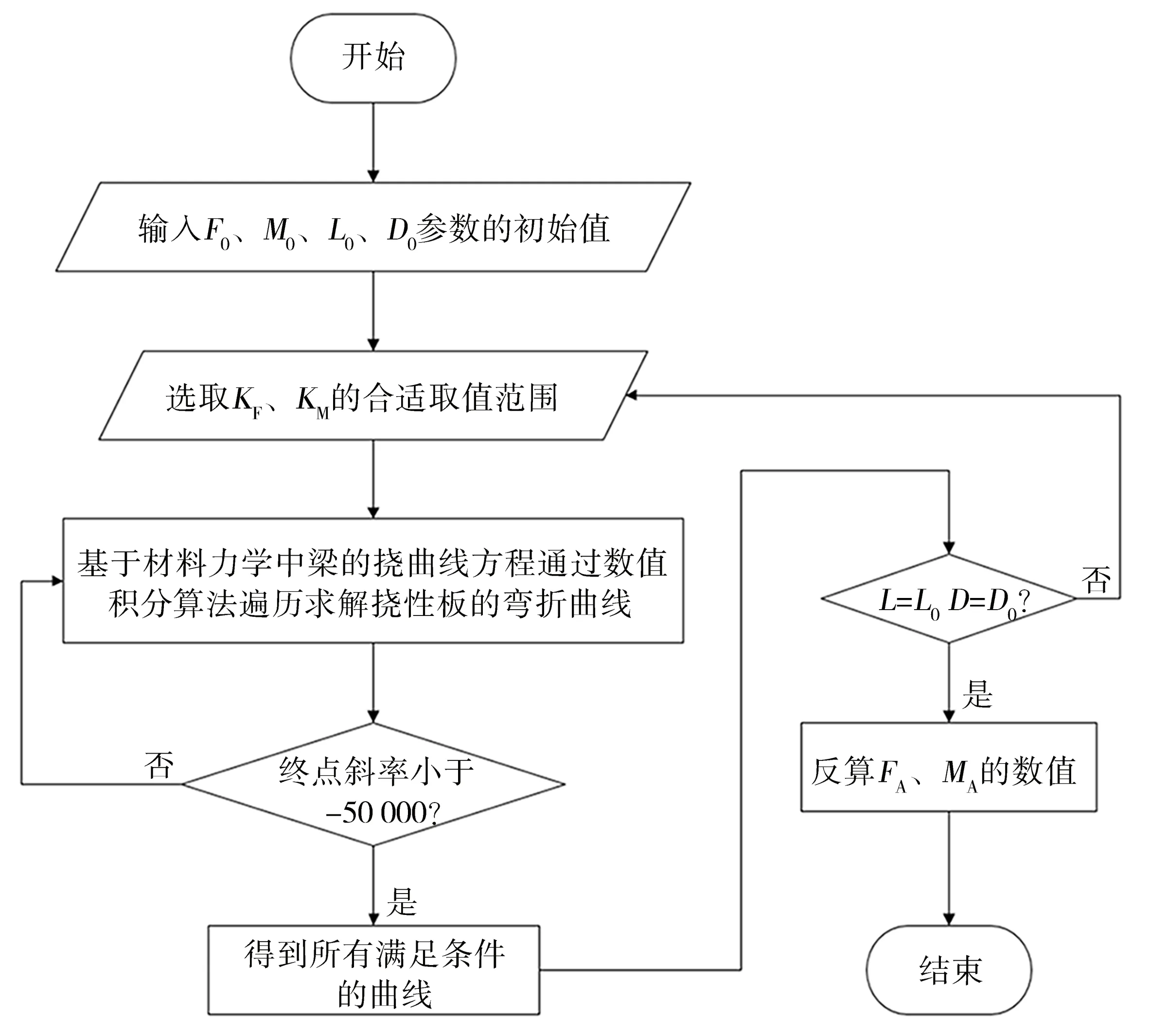
图4 MATLAB数值计算流程图Fig.4 Flow chart of the numerical calculation in MATLAB

表1 仿真计算参数表Tab.1 Parameters of the simulate calculation
对所有的组合分别求解,结果如图5所示。图中数值积分工具对于每个KM和KF值下不同跨度曲线均进行求解,同时曲线构型首先要满足同一长度条件和AC 段(初始段)向下弯曲的条件。边界曲线以下部分为不满足初始段曲线向下弯曲构型的组合,长度条件曲线为满足挠性线长度60 mm 的组合,跨度条件曲线为挠性线弯折后满足相应跨度的组合,两者的交点即为同时满足长度和跨度条件的取值组合(求解精度为1%)。
从图5中可以明显看到随着跨度不断增大,跨度条件曲线向右侧移动,且其右上段逐渐向长度条件曲线靠近,满足相应跨度的取值组合点也在长度条件曲线上向右上方移动。从数值上可以看出:

图5 数值积分结果Fig.5 Numerical integration
(1)D=2R时(本算例中R=60/pi),剪力系数为0,力矩系数为1,符合梁纯弯曲构型时受力状态;
(2)剪力绝对值随跨度增大首先逐渐减小,剪力值减小为0后,剪力改变方向,且绝对值逐渐增大;
(3)力矩绝对值随跨度增大同样先减小后增大,但力矩方向改变时刻先于剪力。
3 有限元仿真验证
为验证数值分析结果的有效性,本文用ANSYS Workbench软件对相同模型进行了有限元求解[12],仿真参数设置同前。得到挠性板弯折至跨度30 和20 mm时的变形和应力情况,如图6所示。
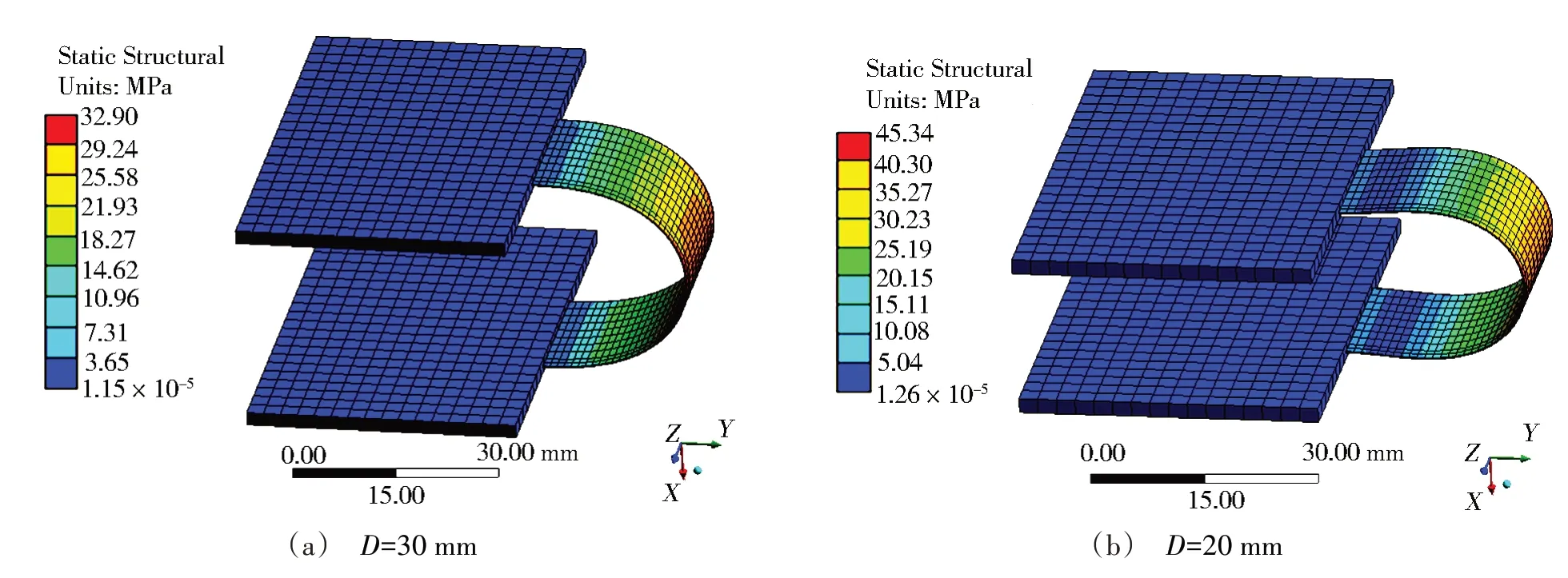
图6 挠性板弯折应力的有限元仿真结果Fig.6 Simulation results of the bending stress of flexible plate in finite element method
取挠性板中间层的变形曲线与数值积分结果,由跨度为30 和20 mm 时的结果对比如图7可见,两条变形曲线非常吻合,对应点处误差最大值在0.2 mm 左右,越接近弯折顶点C(积分末端)误差越大。通过减小积分步长可提高积分精度,减小误差。

图7 弯折曲线的数值积分与有限元仿真结果对比Fig.7 Comparison of the numerical integration and finite element simulation results of the bending curves
跨度为5~50 mm 时两种方法计算的弯矩和剪力结果对比见表2。两种方法的计算结果较为一致,剪力的误差基本在0.024 N 以下,弯矩的误差基本在0.504 N·mm 以下,在两端处误差较大;剪力和弯矩的相对误差基本在9%以下。剪力相对误差最大出现在跨度为40 mm 时(接近圆弧弯曲),此时剪力数值非常小,较小的误差值引起了较大的相对误差。

表2 不同跨度时两种方法计算的弯矩和剪力计算结果对比Tab.2 Comparison of the bending moment and shearing force calculated by two methods in different span
两种方法的误差来源有:(1)积分算法(特别是弧长)的递推公式;(2)积分步长的选择;(3)初始参数的间距;(4)对弯矩和变形方程的简化。后续可从以上几方面入手提高数值算法的计算精度。
4 数值积分结果分析
基于数值积分的结果进一步分析各参数的关系,如图8所示。可以看出:(1)曲线高度H随跨度D增加逐渐减小;(2)KM和KF数值随跨度D增加单调增加且斜率迅速增大;(3)KM和KF呈正相关关系(实际上该曲线即图5中的长度条件曲线)。采用多项式拟合的方式可以获得各参数的近似关系表达式,可应用于后续数值积分的优化,以提高仿真结果的精度。
挠性板弯折曲线的形状与剪力和弯矩符号之间的关系如图9所示。联系图8(c)可知:(1)若FA>0,必然有MA>0,否则不满足曲线的构型,此时有D>2R;(2)若FA=0,必然有MA=M0,此时有D=2R;(3)若FA<0,且MA≥0,此时D<2R,且曲线完全内缩无外扩段;(4)若FA<0,且MA<0,此时D<2R,且曲线存在外扩段(二阶导数先正后负),跨度临界值为27.44 mm。4种状况下跨度依次减小,高度逐渐增加。

图8 各参数关系曲线Fig.8 Curves of the relationship of each parameter
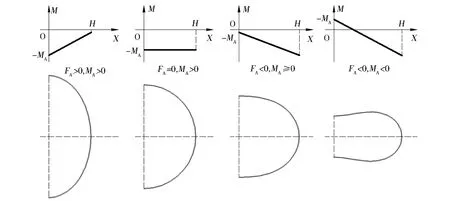
图9 参数符号与曲线形状的关系Fig.9 Relationship of the parameter sign and curve shape
在实际应用中,可以首先根据工程实际需求得到挠性板所需要的初始长度与跨度,然后利用数值仿真根据挠性板的力学性质下以及长度与跨度关系来判断其所承受的剪力与弯矩的方向和数值大小,再以剪应力或正应力为优化目标,在合理的约束下选取一系列可行的长度与跨度参数,最后得到同时兼顾操作工艺性和应力要求的挠性板构型。
5 结论
本文首先对挠性板弯折进行受力分析,然后基于梁的挠曲线方程,将弯矩和剪力作为自变量,利用四阶Runge-Kutta 方法计算了挠性板翻转弯折的曲线构型,最后利用曲线长度和跨度反算来确定弯矩和剪力的数值,仿真计算得到的结论如下:
(1)将数值积分结果与ANSYS Workbench 的有限元仿真结果相对比,发现两种计算方法得到的挠性板变形曲线非常吻合,弯矩和剪力数据非常接近;
(2)基于数值积分结果进一步分析弯矩、剪力与挠性板弯折曲线的跨度、高度间的关系,指出参数符号与弯折曲线构型间的关系,对工程设计具有一定的借鉴意义。
本文发展的数值积分方法可推广应用于挠性板的其他弯折情况,如直角弯折或特定角度弯折。由于支撑反力的增加,自变量数量增加,需要有合适的优化方法配合计算。
