基于改进动态窗口法的无人机避障航迹规划

戴凯龙，贾子彦，潘玲佼

（江苏理工学院 电气信息工程学院，江苏 常州 213000）

0 引 言

避障与航迹规划一直是无人机系统的研究重点，这就对如何控制无人机进行自主导航避障提出了要求。大多数的航迹规划算法中，忽略了无人机的状态和运动学约束。如A*算法、蚁群算法、人工势场法等，规划出的航迹转折较大，无法直接使用，往往需要进行轨迹优化等操作，其代价随搜索空间的维度和复杂度的增大而明显增加。在航迹规划时，应当充分考虑无人机自身的状态和性能变化，使仿真更贴近于实际，增强实际控制的鲁棒性。

动态 窗 口 法（Dynamic Windows Approach，DWA）是一种直接在控制指令空间内搜索最佳控制指令的自主避障算法。根据智能体的运动学特性，得到一系列离散的速度控制组合，并模拟在各控制输入下的轨迹，最后通过最大化目标函数来选择下一刻的最优控制输入。

针对动态窗口法存在易陷入局部最优的问题，很多研究人员考虑将全局路径规划算法与局部路径规划算法相结合。首先通过全局规划算法寻找出一条最优的路径，然后提取路径中的关键节点，最后以局部路径规划算法逐一跟踪这些关键节点来不断朝目标点逼近。但是，该方法存在一些局限性：一是很多情况下的探索任务需要实时进行，无法取得完整的环境信息；二是路径的好坏与全局规划出的关键节点有很大关系，在受到动态障碍物的影响偏离航线后，不能保证不会陷入局部最优中。

基于以上分析，本文针对飞行环境中存在诸多障碍物的情况，搭建了无人机的运动模型，采用动态窗口法来预测避障轨迹，并选择最优的速度作为控制输入。同时针对局部最优问题，给出了一种简单的失效环境判别方法，并通过设置虚拟目标点的方法实现了规避。

1 无人机运动学模型

对无人机进行分析前，需要对模型进行一定的简化，只考虑无人机的质心运动学方程。当无人机存在全向运动时，则在二维笛卡尔坐标系下的运动学方程为：

其中，x，y，θ、分别为无人机当前的位置和偏转角度；v、v为无人机在机体坐标系下，轴和轴两个方向的飞行速度；为偏转速度；为时间间隔；x，y，θ为无人机下一时刻的位置和偏转角度。

2 动态窗口法

根据无人机速度和位置的对应关系，将无人机的位置控制转换为对无人机的速度控制，将避障问题转换成速度空间带约束的优化问题。

2.1 无人机速度空间

同时，无人机在水平飞行存在最大飞行速度和最大偏转速度以及最小偏转速度的限制，速度空间里的速度还应满足式（3）的条件：

2.2 轨迹预测

在预测轨迹前，需要按照一定的速度分辨率和偏转速度分辨率，将速度空间离散成有限的速度组合。在预测轨迹时，保持控制输入不变，即加速度和偏转加速度为0，然后根据式（1）对无人机在每一组速度下飞行一段时间后的轨迹进行预测，同时将其中会与障碍物发生碰撞的轨迹剔除。预测轨迹如图1所示。

图1预测轨迹仿真Fig.1 Simulation of predicted trajectory

2.3 目标函数

为了使无人机能够更好、更安全地到达目标点，通过目标函数对预测轨迹进行评价，其形式如下：

其中，航向得分项（v，v，）度量该条预测轨迹速度下轨迹末端的飞行方向与目标方向之间的偏离程度，其公式为180（为轨迹末端的飞行方向与目标方向之间的角度差）；距离得分项（v，v，）表示该条轨迹到最近障碍物的距离，用来剔除会发生碰撞的轨迹以保证飞行安全，当无障碍物时，将函数值设置为一个常数；速度得分项（v，v，）用于从能够安全避障的轨迹中选择出飞行速度较快的轨迹，其值为合速度的模；，，分别为3个得分项的权重。

在计算完所有轨迹的得分后，需要对每条轨迹的各个得分项进行归一化（σ）处理，然后再相加。归一化的准则是每一项除以每一项的总和。以航向得分项为例，其计算公式如式（5）：

其中，为待评价的当前轨迹，为所有预测轨迹的采样数量。

最后，选择使目标函数值最大的速度，作为下一时刻的控制输入。重复上述过程，直至到达目标点。

3 算法失效环境规避

当目标点出现在“U”型障碍物后面时，容易陷入局部最优，使算法失效。但是，在这种情况发生时很容易被检测到。

3.1 算法失效环境判断

假设无人机可获得周围中等或较低精度的障碍物距离和方位，选取前进方向上一定角度扇形探测区域，作为算法失效环境的判断依据，如图2所示。当障碍物与无人机之间的距离小于阈值R时，分析扇形区域中角度内探测到的距离信息。若角度中没有可通行区域，且距离信息整体呈现“短长短”的形式，则判断前方为“U”型失效环境，需要进行规避，否则判断为一般障碍物，不做处理。

图2 失效环境判断Fig.2 Judgment of failure environment

3.2 基于虚拟逃逸目标点的障碍规避

由于原目标点无法帮助无人机规避失效环境，因此需要人为设置一个虚拟的目标点进行逃逸。另外，这个虚拟目标点应使无人机可达且安全。在一些特殊情况下，可能会检测出没有安全的区域。此时可以对探测信息进行二次处理，从无人机就近的安全区域中寻找逃逸目标点。

将传感器的扇形探测区域按照一定的角度（）均等分割，虚拟目标点从没有障碍物的分块区域中选择，应满足式（6）的要求：

其中，为扇形分块区域与最近障碍物之间的夹角；为扇形分块区域与目标点之间的夹角；，分别为相应系数；为归一化处理。

通过得分选择一个比较安全，且使无人机偏离目标点越小的分块区域的中点位置，作为逃逸时的虚拟目标点。同时增加（v，v，）得分项，使无人机朝虚拟目标点逃逸，其形式如式（7）：

其中，φ为预测轨迹末端的前进方向与到虚拟目标点方向之间的夹角；为失效环境标志量，当判定前方障碍物为“U”型失效环境时，为0，否则为1。

为避免航向得分项在逃逸期间影响无人机，对航向得分项进行修改，其形式如式（8）：

当没有探测到失效环境时，将目标点作为虚拟目标点，同时对目标函数进行改进。

3.3 算法流程

本文算法的具体实现步骤如下：

获得无人机当前的飞行速度和方向，并根据运动学特性，分别计算无人机下一刻所能达到的轴、轴方向的速度，以及偏转速度的范围；

根据速度范围生成速度空间，并在速度空间中，对各个速度进行离散采样，得到一系列速度（v，v，）；

根据无人机的运动学方程，对采样得到的速度进行模拟，进而得到对应速度下的预测轨迹；

根据传感器信息，判断前方飞行区域是否存在“U”型失效环境，若存在则从探测区域中寻找虚拟目标点进行逃逸；否则将目标点作为虚拟目标点进行正常飞行；

采用目标函数对预测轨迹进行评价，然后选择目标函数值最大的轨迹对应下的速度，作为下一时刻的控制输入；

执行最优速度，基于当前位置判断是否到达目标点，若已到达则结束运行；否则返回第一步，进入下一循环。

4 仿真验证及结果分析

4.1 基本参数

为了验证本文算法的有效性，对算法进行仿真实验。仿真环境为MATLAB R2021b，算法涉及无人机自身参数与算法参数。根据实际情况和常规硬件配置，本文选取参数见表1。

表1 算法相关参数Tab.1 Relevant parameters of the algorithm

仿真时将无人机当作质点处理（实际无人机具有一定的体积），因此设置了无人机与障碍物的碰撞距离阈值（仿真阈值为0.5 m），同时当无人机到达目标点半径0.2 m范围内，便视为到达目标点。为了避免逃逸目标点不可达的情况，无人机在逃逸目标点附近1.5 m范围内视为到达。

4.2 避障实验

建立如图3所示的24×24的环境地图，为了避免环境的偶然性，分别设计了两条路线。分别为起点（4，9）到目标点（13，21），以及起点（3，3）到目标点（22，17），黑色方格为障碍物。由仿真结果可见，当目标点出现在“U”型障碍物后面时，改进前的算法面对“U”型障碍物时直接陷入了局部最优，而改进后的算法通过虚拟目标点，实现了逃逸，并最终到达目标点。

图3 算法仿真图Fig.3 Simulation diagram of algorithm

4.3 动态环境实验

为了验证本文算法在动态环境中的性能，仿真结果如图4所示。在环境中加入一些动态障碍物（图中的红色圆）后，无人机飞行时不但能够躲避环境中的动态障碍物，同时还能够避免因躲避障碍物而陷入局部最优的情况。

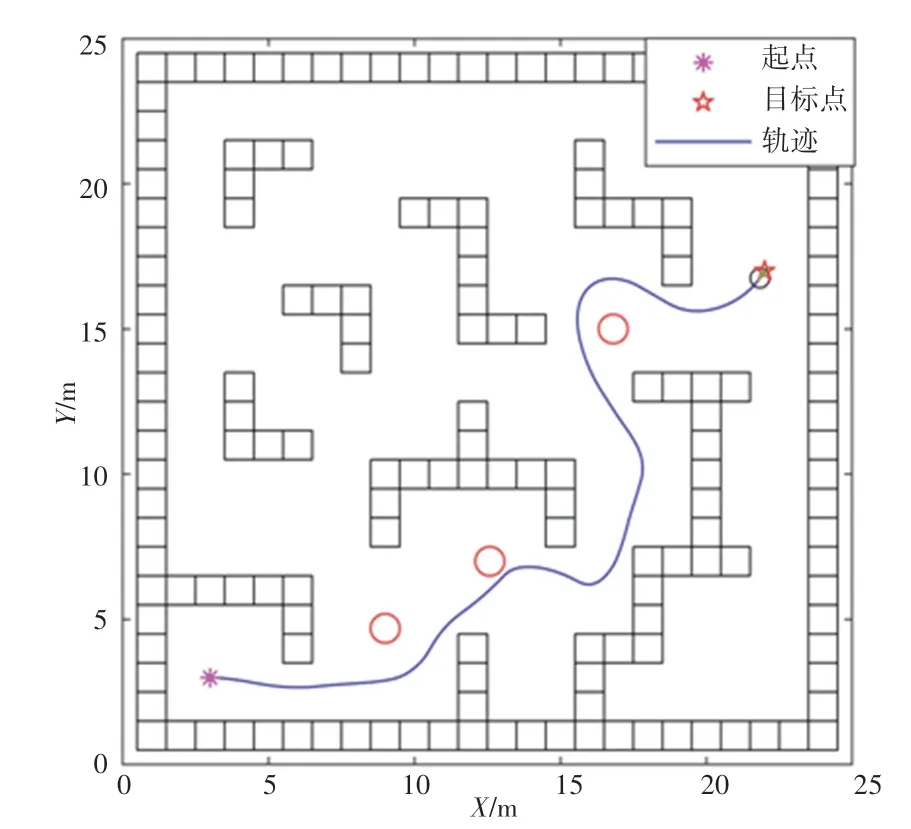
图4 动态环境实验Fig.4 Experiment in dynamic environment

5 结束语

本文考虑了无人机带有运动约束情况的避障问题，使用动态窗口法来寻找最优的避障路径，同时提出了一种依靠局部环境信息来规避“U”型失效环境的方法。仿真结果表明：本文算法能够使无人机在避障规划时避免陷入局部最优的情况，实现了在动态复杂环境中的自主飞行。