以“关系”为径,整体认识运算意义
2022-07-15林红
林红



摘 要:以“关系”为路径学习数学知识,可以从数学结构、数学思想的高度审视小学数学。培养数学中联系起来分析问题,找条件和问题相互间的关系,对数学学习有提纲挈领的作用。“四则运算的意义与关系”一课,从“找关系”入手进行深度学习,有利于建构知识网络,减轻学生记忆知识的负担,提升思维水平。
关键词:找关系;整体认识;提升思维
大百科全书(数学卷)对数学的定义是:研究现实世界数量关系和空间形式的科学,它包括了数的关系、量的关系、形的关系。因此,以“关系”为路径学习数学知识,可以从数学结构、数学思想的高度审视小学数学。培养数学中联系起来分析问题,找条件和问题相互间的关系,对数学学习有提纲挈领的作用。
为了准确把握学生对知识的理解程度,并有效利用学生的学习资源,在“找关系”为学习路径的理念指导下,笔者设计了课前导学单。
笔者把学生答题情况分为三个层次。第一层次:100%的学生六道题能正确列式解答。第二层次:80%的学生能试着用图示或自己的语言表示每一种运算的意义,能写出每一种运算各部分的关系,但由于缺少对运算内部关系的深入思考,所以难以写全各部分所有的关系。第三层次:最后一题,找四则运算相互关系中仅20%的学生能用自己语言表述对加减或乘除之间相反关系的感悟,没有学生对四则运算关系有整体认识。因此,笔者把这节课教学提升点设定为:通过“找关系”能让学生把四则运算的意义联通起来进行整体认识,充分感悟四则运算的内部的关系和相互关系,并能通过实际问题的解决,提高“关系”灵活运用的能力,从中感悟“逆”和“简”两种数学思维方法。
一、题组的对比教学,体验“逆”关系
(一)找“题—图—式”的纵向关系,概括加法意义
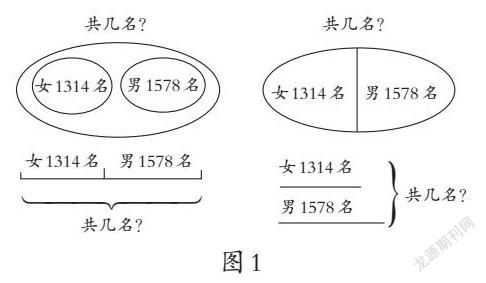
从数学逻辑上来分析,建构加减法以及乘法的定义必须从加法切入,所以加法意义的理解是基础。笔者通过对学生课前导学单中第1题作品的收集,整理了图1,引导学生在读清题中的条件和问题的基础上,迁移到与直观图建立联系,数形结合理解图示中每一部分的意思。再比较4个图示的共同点,联系加法算式,学生很自然地感悟到:把两个数合并成一个数的运算叫加法。“逆”向理解:这“一个数”是一个整体,“两个数”是一个整体的两个部分。这样就得出加法算式中各部分的名称和关系:和=加数+加数。“逆”向理解得出另一个关系式:一个加数=和-另一个加数。从整体和部分的关系深入理解加法的意义,还从“逆”的关系角度完整列出加法各部分关系式。
(二)找题组中“条件问题”的横向关系,逆向定义减法意义
通过题组中3道题条件和问题的对比,减法算式中每个数与加法算式中每个数位置的对比,学生概括出减法的意义和内部各部分关系。观察加法算式中的和就是减法中的被减数,加法中的一個加数就是减法中的减数,加法中的另一个加数就是减法中的差。学生深入分析:原来不仅减法各部分之间有联系,加减法各部分之间也能联系起来。看到学生已经有了联系地分析问题的思想与能力,笔者出示学生在导学单中概括出的“从一个数中去掉一部分,求另一部分是多少,叫减法”,让学生辨析:这样概括减法的意义,你们认为可以吗?学生分析:从部分与整体的关系角度来看,也完全是正确的。还有学生分析:一个数其实就是已知两个数的和,一部分就是其中一个加数,另一部分就是另一个加数。书中的定义是从加法逆向思考得到的,这个同学的定义是从减法本身的意义得到的。能从这些角度分析,说明这时学生对加减的意义与关系不仅能互推,而且能融合,对加减法的整体认识很深入。
二、升级运算等级,体验“简”关系
(一)从“加”升级到“乘”,感悟乘法是相同加数连加的简便运算
加减是一级运算,乘除是二级运算,它的优先级比加减高一级,怎样体现进阶的关系呢?在导学单中学生第二组题第一题的解题策略都是乘法,引导学生思考,这道题还能用别的方法解决吗?学生回答:也能用加法,五百五百地数。追问:为什么所有的同学都用乘法做呢?学生回答:因为求4个500的和是多少,用乘法更简便。所以乘法的意义就是求几个相同加数和的简便运算。
数学的发展就是不断地用更有效、更高级的方法代替原有方法的过程。“数—加—乘”算法提升的过程,使解决问题的过程越来越简单。从数学运算的发展来看,乘法比加法高一级,计算效率也提高一步,归根结底是缘于计算的简便。学生搞清楚乘法与加法的联系,就形象类比:就像走台阶一样,有了下面的第一级,才能有上面的第二级,所以乘法是比加法更高级的运算。
导学单中学生出现对乘法意义的另一种归纳:求一个数的几倍是多少,用乘法。怎样把这个学习资源同化到乘法意义中呢?学生分析道:书中的定义是以加法为基础的,更体现了加法到乘法的进阶关系。学生概括的意义就是从乘法的倍数角度,也是对的。还有学生分析:求2的3倍是多少,就是求3个2是多少,也是求几个相同加数和的简便运算,能联系起来的。这样,点联系成了一条线,就把对乘法零散的认识串联起来,对乘法意义的理解更深刻。
(二)从“减”升级到“除”,感悟除法是递减相同减数的简便运算
根据“逆”思维迁移,类推除法意义与各部分关系。除法的“简”也是学生利用“加和乘”的联系推出来的:一个数,如果不断地减相同的数后,没有剩余,就是整除;如果还有剩余,就是有余数的除法。通过“找关系”,联系地分析,有了前面的引导,学生能够沿着这个路径,自己发现和创造出新的结论。
三、关系图是四则运算整体认识的精准表达
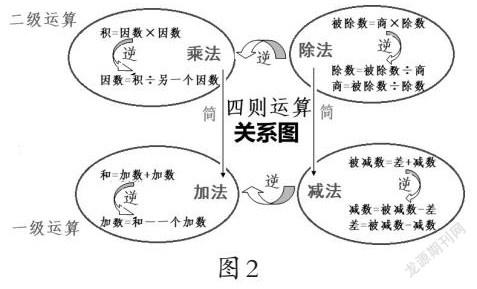
整节课开辟了“关系”路径,最后让学生再次尝试导学单的最后一题,用图示表示四则运算的联系。通过学生不断讨论改进后的关系图(图2),全面总结本节课的内容,建立四种运算相互关系路径,沟通思维渠道,为知识建构提供新的视角。
四、“关系”路径的综合应用,感悟价值
(一)课内练习,方法灵活适用
数学书和《作业本》里的练习题思考性很强,只有把所学知识融会贯通,培养学生有联系地分析问题的能力,才能更好解决问题。
1. 关系运用要整体性和熟练性
如:猜猜水果后面藏着几,填一填。
要解决这种题,先要判断各图形在原题里是什么数,应该使用该运算内部的什么关系。在计算过程中最后两小题既有运用运算内部关系,又有“有余数除法”中求被除数要除数乘商还要加余数;还有求除数,用被除数减余数的差才是除数与商的积,强调等号左右“对应”的思想方法,为五年级的方程学习打下基础。
又如:已知★-▲=◆,☆÷◇=△,下面哪些算式是正确的?正确的画“√”,错误的画“×”
(1)★-◆=▲( )
(2)▲-◆=★( )
(3)◇+△=☆( )
(4)☆÷△=◇( )
這道题把两种运算放在一起辨析,信息干扰性比较大。其中1、2、4小题直接用运算的内部关系判断,第3题要用到除法和加法的相互关系。解决问题时,关系运用要熟练,对关系的整体认识要强,这样的题符合四年级下册学生的思维水平。
2. 感悟方法的灵活性和适用性
解决看似相同的题,方法的运用可能是不同的,在学生实际解题过程中,不断让学生总结自己的思考方法,选择更合适的方法。
例如:琳琳想了一个数,按下面的指令进行计算,得到的结果是25,琳琳想的数是( )。
这道题用“逆推”能高效解题。
又如:进入知识宫的密码是○□○□,请先破译密码。
14+82-○=87
□×6+10=58,
密码是( )。
关于○的解法,有的学生用了“被减数=差+减数”的关系,有的学生用了“减数=被减数-差”的关系,这两种方法仅仅是观察角度不同,其本质都可以归结为减法算式内部的各部分关系,○的解法不适用逆推。而□的解法,有的学生回答:我用了“逆”的思考方法,58-10=48 48÷6=8。有的学生回答:我用了“加法各部分的关系”思考。学生不仅会选用合适的方法,而且能清晰地表达自己选用的思考方法,能反映学生头脑内部知识网的建构在应用中体现价值。
(二)拓展数域,知识整体建构向课外延伸
小数、分数的四则运算的运算意义与关系,与整数四则运算的运算意义与关系是完全相同的。打通它们之间的“隔断墙”,为整体性、系统性学习再深入一步。根据学生在导学单里提出的“我想提出的问题:整数的四则运算方法和小数、分数的方法一样吗?”可以让学生猜想,并带着问题进行课后探索,把课堂内的学习向课堂外延伸。
一节概念定义和已有知识梳理的课,通过单元整体架构,挖掘内在联系,渗透数学思维方法,使学生得到深度学习,提升思维水平和语言、图示的多元化表达能力。
