“正者知其原,误者晓其因”
2022-07-15侯海全万书河钭斐玲
侯海全 万书河 钭斐玲
在教育目标分类学理论的指导下,通过对一道试题的问题情境、学生正解和典型误解进行分析,以明确“正者知其原”,即做对题目的学生知道为什么能做对;“误者晓其因”,即做错题目或不会做的学生知道为什么做错或不会,可以改变教师直接将解题过程讲授并大量“刷题”的局面,真正提升课堂教学质量并切实减轻学生学习负担。这样以“分析完成解题任务需要用到的知识要素、方法和策略”为特征的课,我们称为“析题课”。
我们以八年级上册“全等三角形”中的一节析题课为例进行研究。
1.教学内容及教学对象分析
全等三角形在几何体系中有着重要的意义,其相关基本事实占初中平面几何学习的九条基本事实的三分之一,其相关概念与定理既用到前面直线、角、平行、垂直等知识,又将作为后续学习等腰三角形、四边形、圆等内容的基础。在全等三角形的学习和应用过程中,画图与作图、推理与运算以及数学建模等能力始终伴随其中,承载了培养学生基本能力的功能。对全等三角形的学习和考查,从教育目标分类的角度看,实质上是完成具体情境的认知任务,要求学生不仅能够依据所给条件主动搜索记忆并提取相关概念、原理等知识,还要知道解答此类题目常用的思路或模式。
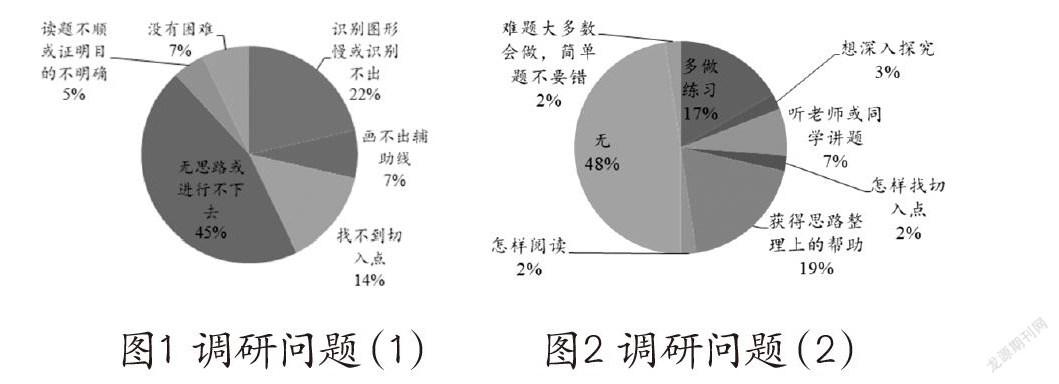
我们对学生进行了调研:(1)在几何学习过程中,你遇到过哪些困难?(2)在几何学习过程中,你希望获得哪些帮助?通过调研(调研结果如图1和图2),了解学生在几何学习过程中的主要障碍和困难,了解学生在已有学习经验基础上的需求。
学生遇到的困难主要表现在思路、图形、切入点、辅助线、问题情境等方面,近一半学生存在无思路的困难,近一半的学生希望获得思路、听题目讲解、找切入点等方面的帮助。
2.析题课的课前准备
设计若干典型的认知任务进行简单测试。例如,在此次全等三角形析题课前,我们设计了7个典型的认知任务。
选择典型认知任务作为分析对象。统计学生完成情况,并分析结果:近98%的学生具备较为扎实的知识基础,能够解决简单几何问题,只有约38%的学生能完成较复杂的几何问题。过难或过易的题都不适合在全班范围进行分析,我们选择完成率在30%至70%的题目作为析题课的分析对象。
选择规正的学生解答和典型误解为教学材料。我国著名数学教育家傅种孙先生说过:教学的技艺,一方面要指示正规,一方面要矫正错误,必须两者兼施并用,方会有好的效果。因而析题课一方面分析正规的解题过程中每一步涉及的知识要素以及整体思路流程,也就是“析正解”。另一方面是选择学生典型误解作为教学资源提供给学生,用来分析错误原因,并且思考和寻求正确的解决策略,也就是“纠误解”。“析正解”和“纠误解”的学习活动先后进行,有利于学生深入、理性地分析和评价,提高数学学习的自我效能。
3.析题课的教学目标
本节全等三角形析题课的教学目标如下:(1)通过对全等三角形综合题的题目和解答的剖析,能够分析出每步推理蕴藏的知识要素,根据解题思路画出相应的流程图;(2)通过对经典正解和典型误解的分析,明确“对之何以对,错之因何错”,提升推理能力和分析能力;(3)通过个人独立思考、小组交流、集体汇报等活动,树立学好数学的信心,更好地认识自我与他人,促进个人的发展与提高。
4.析题课的教学流程
活动一,分析数据,明确对象。
展示课前7个典型认知任务的得分率,确定本节课要分析的几何问题。
师生活动:教师以条形图的形式反馈学生在已完成的认知任务中各小题的整体情况,与学生共同确定本节课想要分析的几何问题,同时教师明确本节析题课的目的。
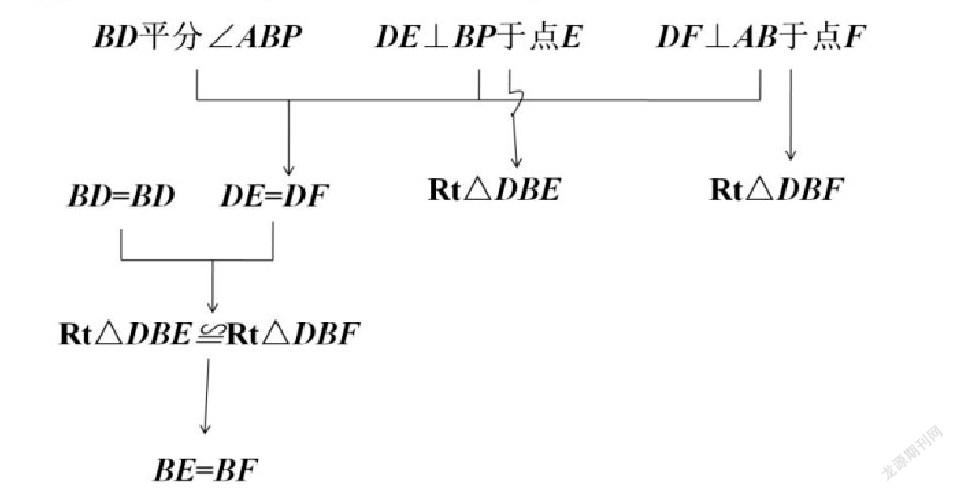
试题:BD平分△ABC的外角∠ABP,DE⊥BP于点E,DF⊥AB于点F。
(1)求证:BE=BF;
(2)若∠DAB=∠DCE,探究AB,BE,BC的数量关系,并证明。
活动二,揭示正规,明了方法。
展示第1问的正确解答过程,结合解答过程,写出题干(已知)、问题(所求)及第1问解答过程中推理的依据。
任务2.1 独立分析。学生按照活动二要求对问题情境及第1问解答过程中用到的推理依据进行独立分析。
任务2.2 小组交流。学生在与组内同学交流的过程中认同和修正自我,依据讨论情况确定代表,进行展示。
任务2.3 展示汇报。1-2位学生代表分享小组活动二情况。
任务2.4 思考归纳。教师追问:“对于同学的分享,你是否有不同意见?”学生达成一致意见后,明确已知、所求、推理依据是解决问题的基础。教师追问:“清楚这些已知、所求、推理依据之后,问题是否就能得到解决?”明确杂乱无章的知识无法真正解决问题,需要依据图形将它们有目的地组织起来(如图所示)。
这样的思维流程图建立在情境分析、知识间联系的基础上,能够呈现解答第1问时用到的知识和思路,使得解决问题的方法和思路更加清晰。
师生活动:学生通过独立分析、小组交流、展示汇报三个阶段完成活动二,教师在巡视和倾听过程中指导、帮助和启发学生。教师以问题串引导学生进一步认识到解决问题的基础和知识组织过程的重要性。
活動三,关注联系,查找缺失。
参照活动二的分析过程,继续分析情境,并尝试呈现第2问中的思维流程图。
任务3.1 独立分析。在活动二的基础上,对问题情境进行再分析,并结合图形尝试有目的地组织知识解决问题。
任务3.2 小组交流。学生在与组内同学交流的过程中认同和修正自我,依据讨论情况确定代表,进行展示。
任务3.3 展示汇报。1-2位学生代表分享小组活动情况。
任务3.4 思考归纳。教师追问:“在知识的组织过程中,起到重要作用的因素有哪些?”。再次明确已知条件、所求结论、推理依据是解决问题的知识基础,同时图形结构影响了知识如何组织起来。再追问:“要成功解决几何问题,你认为要做哪些事情?”明确解决几何问题的基本方法。
师生活动:学生通过独立分析、小组交流、展示汇报三个分解任务完成活动三,教师在巡视和倾听过程中指导、帮助和启发学生。教师以问题串引导学生进一步思考和归纳,明确解决几何问题的基本方法。
活动四,矫正失误,加深认识。
参照活动三中的分析方法,为两位学生的不完善的过程指出问题并给出建议。
任务4.1 独立分析。在活动三的基础上,对他人不完善的解答过程进行分析,指出问题并给出建议。
任务4.2 小组交流。学生在与组内同学交流的过程中认同和修正自我,依据讨论情况确定展示代表,进行展示。
任务4.3 展示汇报。1-2位学生代表分享小组活动情况。
活动五,回顾反思,总结策略。
通过本节课,你有哪些收获?对你今后的学习有哪些帮助?
5.对析题课的反思
这样的析题课与以往的复习课相比有哪些不同之处?析题课在课前对学生进行了调研和检测,建立在学生的需求上,对题目、知识和方法的分析、检查和评价,以解决学生的困难和提升学生能力为目标。
这样的析题课给出了题目的正确解答过程,目的和好处是什么?给出题目的正确解答过程即是指示正规。对于没做出这道题目的学生,给出题目的正确解答过程让学生深入分析,有助于他发现解答问题中需要用到的知识,促使他关注知识间的联系;对于做出这道题目的学生,在这样的分析过程中,学生学到了分析方法,同时也关注到知识间的联系。
在这样的析题课中,指示正规和矫正错误兼施并用,教学时间不足怎么办?对于知识要素较少、思路相对简明的题目,指示正规和矫正错误能够在一节课中完成;对于比较复杂的题目,仍要保证学生充分的学习活动时间,可以将指示正规和矫正错误分解在两节课中完成。析题课之后可以对同样知识要素的不同题目进行检测,以检验课堂教学效果,如仍出现普遍性错误,我们可以进行再分析和再评估。
编辑 _ 李刚刚
