基于目标分类的数学解题教学的思考

康杰 黄炜 刘洁

- 编者按 -

“双减”不只是减轻学生的负担问题，其深层意蕴是教育本质的回归、教育规律的彰显，直接指向校内教育尤其是课堂教学质量的进一步优化改革。“双减”下如何高质量开展课堂教学，回归育人本质，彰显育人规律？这是所有教师都会面临的现实问题。本刊将陆续呈现各学科优秀教研成果，以期为教师高效开展课堂教学助力，为落实“双减”要求蓄能引航。本期，我们推出的是初中数学学科教学中“基于目标分类的数学解题教学”方面的探索。

提高课堂教学质量是落实课程标准、发展教师专业能力和提升学生学业水平的需要。为此，《关于深化教育教学改革全面提高义务教育质量的意见》指出：强化课堂主阵地作用，切实提高课堂教学质量。[1]

纵观中国初中数学教育教学的历史，在课程标准和教学大纲中的作业往往指课堂练习和课外练习两种，关于课外作业的表述不多，但对课堂练习的建议写得比较详细。例如，1929年《初级中学算学暂行课程标准》中的“作业要项”提出了“课室练习”应“每次黑板上的练习以后，应有时间说明算式和解释的理由”，“课外练习”应“课外单纸上的练习可与同班讨论，但要自己懂得‘学习心理’的历程的重要，不应抄袭别人的演草”。又如，1932年《初级中学算学课程标准》中的 “作业要项”提出了“教师练习”应注意“初中学生对于算学一科，最感困难，宜在教室，多予练习与复习之机会，务使学生课外作业时间，得以减少”。再如，1992年《九年义务教育全日制初级中学数学教学大纲（试用）》中的“正确组织练习”指出“为了使练习能起到应有的作用，应注意以下几点：（1）目的要明确，题目要精选。（2）题量要适度，首先要保证有足够的基本题。析题难度要适中，布置作业要区别对待。对学习有困难的学生，要给予必要的辅导…”[2]上述材料显示了初中数学教育教学中练习和解题的重要，也反映出练习不当是学生学习压力过大的主要因素。

1.学生数学作业负担过重的原因分析

笔者通过对部分北京市中学生的调研发现，学生认为数学作业负担过重的原因不在于数学作业多，而在于看似不多的题量，却需要耗费大量的时间和精力，甚至有学生形象地比喻道：做数学一道题的时间等于其他有些学科一张卷子的时间。

产生以上问题的原因主要有两点，一是数学自身的学科特点决定的。数学的公理化和形式化要求学习者具有较高的逻辑思维和抽象能力。数学的原理（公式、定理等）所具有的广泛应用性和数学方法具有的灵活性又导致了学生在解决具体问题时遇到障碍，常常觉得可用的方法很多，但真正用得上的很少。二是目前的数学解题教学中存在的问题造成的。在当下评价背景下，解题是基本形式和主要内容，出其不意、攻其不备的命题方式也促使师生陷入题海之中。

在解题教学实践中，“该选用什么样的例题”“为什么很多典型问题反复讲解后学生依然难以解决”等问题长期困扰着广大一线数学教师。涂荣豹教授认为，在数学解题学习中，学生的主要任务并不是解题，而是学习解题，因此，教师教的重点和学生学的重点，不在于“解”而在于“学解”，以“解”作为出发点，注重的是解题的结果，以“学解”作为出发点，注重的则是解题的过程[3]。

2.解题教学的研究简述

梳理发现，目前的解题教学研究的方向主要聚焦在两个部分，即研究解题教学本身与研究解题教学的解题方法与技巧，前者的研究主体主要是教学研究人员，而后者主要是广大一线教师。

关于解题教学的研究，最重要的代表人物就是美籍匈牙利数学家波利亚，他专门研究了解题的思维过程，并形成了解题理论。在1944年出版的专著《怎样解题》（How to solve it）中提出的“怎样解题表”总结了人类解决数学问题的一般规律和程序，对数学解题研究有着深远影响[4]。自波利亚的解题理论传入我国以来，对我国数学教育亦有着极其重要的指导意义，也给我国中学数学的教材及教法带来了很大的转变，徐利治所著的《数学方法论选讲》被认为是波利亚“怎样解题”研究的延伸与发展[5]。罗增儒与罗新兵在其《波利亚的怎样解题表（续）》中详细概述了解题系统，分析解题过程，念头诱发，问题转换，朴素的元认知观念与波利亚怎样解题表的关系，并揭示了波利亚解题思想的目标，即发现和发明的方法和规律[6]。在此基础上提出有效的解题教学策略，并形成行之有效的教学模式正是我们研究的方向。

3.基于目标分类的数学解题教学探析

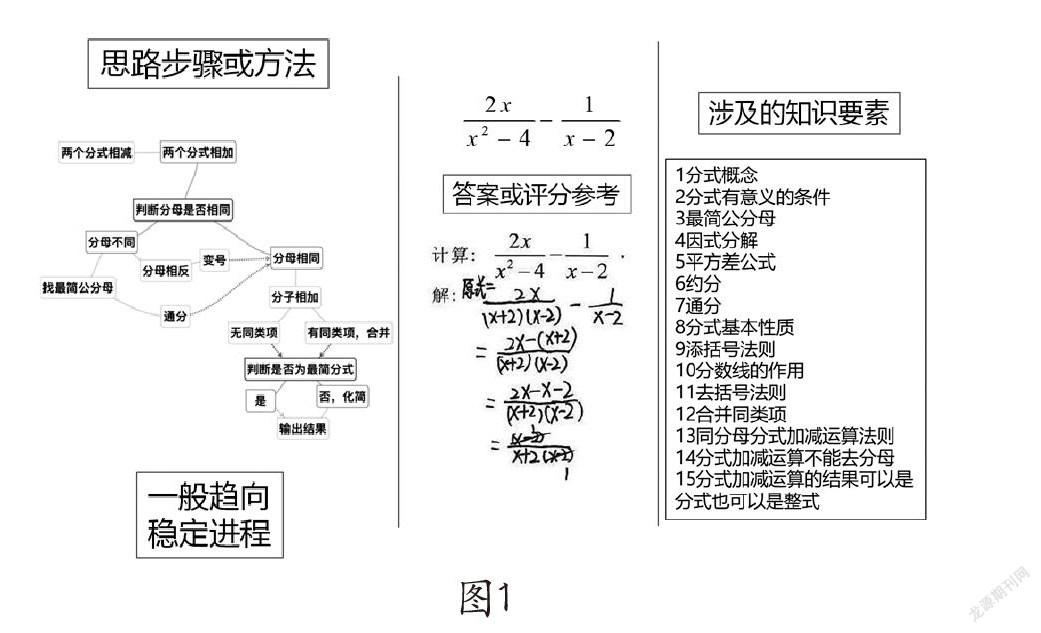
要从根本上提升教师的解题教学水平和能力，进而切实提高课堂教学质量，就需要将教师自身置于解题思维活动中，体验学生的解题过程，分析我们面对题目时的表现。为此，我们借鉴了心理学建立初期常常采用的一种方法——内省法，检查自己解决数学问题时的想法，进而推断学生的想法，如图1所示：

这是一道分式运算的题目，图1中间一列显示的是一位学生的解题过程，右边一列显示的是在解答这道题目的时候，我们的大脑需要提取的相关概念、法则、公式等多种知识要素，如果有一个或几个知识要素不能被正确提取，那么解题过程必然会出现各种错误。在解答这道题目时，大脑还需要将这些概念、法则、公式有机地联系在一起，形成思路、程序或方法，如图中左边一列用图示的方法直观呈现分式加减法的思维过程。

如果我们从教育目标分类的角度认识如何解答题目，我们会发现，在解题过程中涉及的知识有概念、法则和公式等，这些知识都属于事实类知识和概念类知识，而我们的解题思路或者解题方法，则属于程序类知识，是指某些具體的操作步骤，某种固定的操作顺序，运行之后能得到结果。弄清知识的类别，对于我们解释和分析如何解答一道题、题目能否正确解答及不能正确解答题目的原因，有着重大的意义和作用。从知识分类的角度，还有一类重要的知识——元认知，其中有一种元认知知识称为认知任务的知识，主要包括：“知道不同的认知任务可能难度不同;知道不同的认知任务可能对认知系统提出不同的要求;知道不同的认知任务可能要求不同的认知策略”[7]。在解题活动中，我们将解题思路、步骤简称为“认”，把用到的概念、法则、公式等知识要素简称为“知”，将具体题目的解答过程看作一个“任务”，那么这三类知识共同构成了认知任务知识（如图1）。

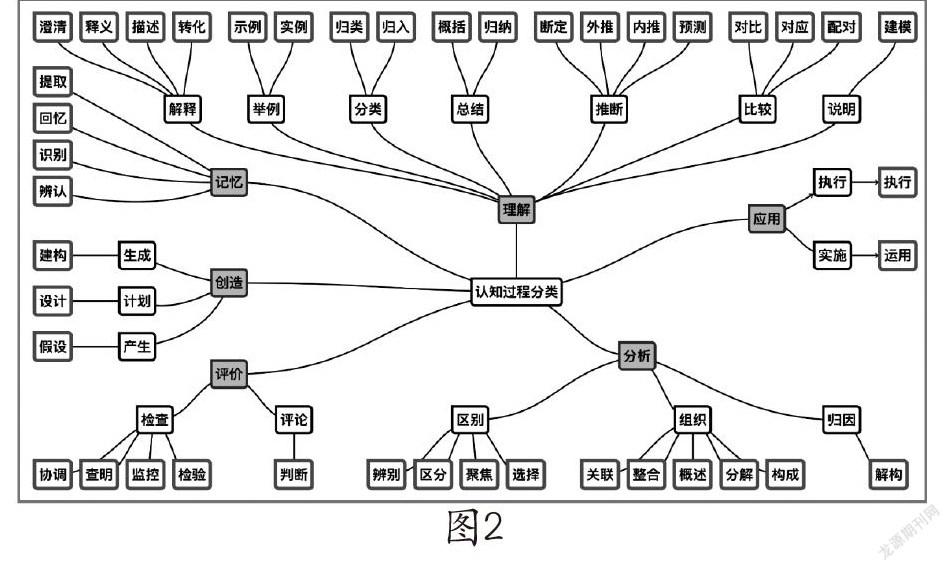
学习认知任务知识需要经历哪些思维活动呢？这就需要我们再从另一个角度分析——认知过程的分类。如图2，在认知过程的分类中，我们常常把记忆、理解、应用称作初级认知加工。在做题过程中，需要先提取相关知识，而提取的前提是能够在理解的基础上进行记忆，再将提取的知识进行有步骤的应用。如果我们不是应用知识解题，而是对一道题目或任务的解答过程进行研究，分解其中的具体操作步骤，辨别具体操作步骤的依据，概述解答过程的流程，我们就进行不同于记忆、理解和应用的认知加工，这种认知加工就是分析，也称为分析能力。

当我们以认知任务知识和分析能力为教学目标时，我们就得到了一种新的课型——析题课，其中的“析”字主要是指分析的意思。在析题课中，最重要的任务不是让学生做题，而是要给学生题目和解答，让学生先分析题目解答过程中用到了哪些具体的知识，在这个基础上，再对解答过程进行概括和总结，用图示的方法直观表示解题思路。

教师如何上好一堂数学解题课，让学生脑海里的知识得到应用，使得“正者知其原，误者晓其因”，从而有效减轻不必要的课外作业负担，正是本文所研究的课题。

参考文献：

[1]中共中央 国务院. 关于深化教育教学改革全面提高义务教育质量的意见[EB/OL].（2019-06-23）[2022-02-20]http：//www.gov.cn/zhengce/2019-07/08/content_5407361.htm.

[2]课程教材研究所编.20世纪中国中小学课程标准教学大纲汇编（数学卷）.人民教育出版社，2001年.

[3]涂荣豹.数学解题的有意义学习[J].数学教育学报，2001（10）.

[4]G·波利亚著.怎样解题[M].涂滞，冯承天译.上海科技教育出版社，2007.

[5]徐利治.数学方法论选讲[M].武汉：华中工学院出版社，1983.

[6]罗增儒，罗新兵.波利亚的怎样解题表（续）[J].中学数学教学参考，2004（05）.

[7]洛林·W.安德森等编著. 布卢姆教育目标分类学（修订版）[M]. 北京：外语教学与研究出版社，2009.