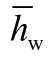气体管流到达西流的缝高界限实验测试与理论计算

熊钰，傅希桐，李骞，孙泽威，张春，张飞

（1.西南石油大学油气藏地质及开发工程国家重点实验室，成都 610500；2.中国石油西南油气田公司勘探开发研究院，成都 610041）

0 引言

近年来碳酸盐岩气藏探明储量不断增加[1-2]。碳酸盐岩具有复杂的孔缝洞结构，地层裂缝较为发育且裂缝沟通能力强。流体在不同开闭程度的裂缝内的流动状态变化复杂，给气藏勘探开发带来很多难题。

为了充分了解裂缝的导流机制，需要进行模拟裂缝流动的测试，但国内外没有统一的测试标准和方法。许多学者对此开展了多方面研究[3-6]，但仍存在诸多不足，例如制作的模拟裂缝较大，裂缝面较宽，没有形成具有标定性质的裂缝组，无法横向比较。对于裂缝内流体流动的计算方程，国内外也有不同的研究结论。有学者基于非线性 Izbash定律描述气体在自支撑裂缝中流动的特征方程，或基于流动特征方法建立自支撑裂缝导流能力计算公式[7-8]，但未结合裂缝缝高相关参数。陈国灿[9]用差分方法模拟二维裂缝性多孔介质中的单相达西流动，求解基于降维模型推导的流体流动方程，但未考虑流动状态的变化。Zaouter等[10]从Navier-Stokes方程、连续性方程和气体状态方程出发，建立考虑雷诺数的裂缝面的流量-压力-梯度关系，但未区分流动状态。Espinosa-Paredes等[11]对裂缝性多孔介质进行了标度分析，确定了裂缝性多孔介质研究的特征尺度，划分不同区域，建立裂缝流动的连续性方程。Vu等[12]建立了描述流体在多孔介质中流动的单一边界积分方程。Chen等[13]利用双参数方程对Forchheimer非线性系数对峰值粗糙度的依赖性进行了敏感性分析，证明在非达西流动模型的发展中考虑裂缝粗糙度的重要性，却忽略了裂缝自身的材料性质。综合来看，虽然国内外学者对裂缝内流体流动和导流能力计算进行了广泛研究，但还没有形成适合界定裂缝内流体流动形式的方法。因此，有必要结合非线性流动模型与流体力学基本规律，建立针对裂缝内流动状态转换界限标定的实验评价方法，对裂缝导流能力进行深入研究。

本文针对碳酸盐岩气藏开发需求，开展不同缝高裂缝的流动模拟实验，确定裂缝由于缝高的减小而产生的流动状态的变化，明确流动状态的转换形式，找到流动状态转换界限和转换区间，以准确指导不同开闭程度裂缝的导流能力计算。

1 裂缝流动模拟实验

1.1 实验材料

为了模拟地层微裂缝中的气体流动状态，需要考虑实验模拟裂缝面与真实地层裂缝面的相似性，从裂缝面微观形貌、对气体分子吸引力两个方面讨论了其相似性。

1.1.1 微观形貌对比

实验采用内径为0.32 mm、长为40 cm的H65-Y型超细铜管模拟裂缝（见图1a），将其剖开（见图1b），使用场发射扫描电镜获取铜管内表面微观结构图。可以看出，实验采用的电火花穿孔的铜管内部并非绝对光滑，存在不同高度的微凸体（见图1c），与实际地层中岩石裂缝面由于存在不同大小的岩石颗粒而不绝对光滑相符合（见图1d）。

图1 铜管裂缝连接及扫描电镜照片

1.1.2 对气体分子吸引力对比

为对比实验铜管壁面和碳酸盐岩裂缝壁面对气体分子吸引力的相似性，采用Lennard-Jones方程[14]计算固体壁面对气体（如氮气）分子的吸引力，具体计算方法详见文献[14]。计算了不同距离下壁面对氮气分子的吸引力，如图2所示。可以看出，随着距离的增加，吸引力越来越小，距离超过40 nm以后两条曲线基本重合，说明实验中铜管壁面和真实碳酸盐岩裂缝面对气体分子的吸引力具有较高相似性。氮气的分子质量为 4.56×10-23g，由此可算出氮气分子重力为 4.557×10-27N。当壁面对分子的吸引力与氮气分子重力的比值小于 1时，氮气分子将不被固体壁面吸附。由于氮气分子直径为0.364 nm，可得到标准状况下铜管壁面对氮气分子的最大吸附距离为162 nm，白云岩壁面对氮气分子的最大吸附距离为265 nm。相较于实验中毫米级的缝宽，吸附距离均可忽略，两者在这方面同样具有较高的相似性。

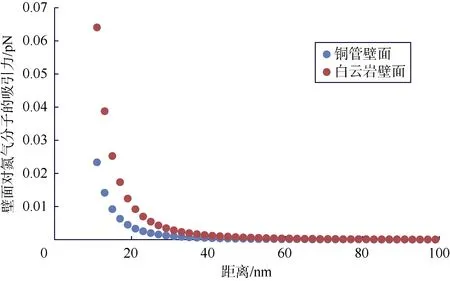
图2 不同距离下壁面对气体分子的吸引力

1.2 实验方法

首先，对铜管进行不同程度的压扁处理以模拟地层中的微裂缝。然后，使用托环压箍（用四氟乙烯材料制作）将压好的铜管裂缝与金属转接头连接，保证密封性，再将金属转接头接入实验气源瓶。最后，在不同入口端压力下将氮气注入铜管裂缝，计量出口端的流量和出、入口端的压力。实验装置如图3所示。

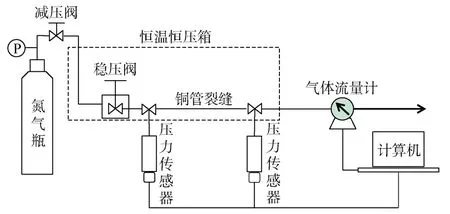
图3 实验装置示意图

由于铜管的最大承压为 1 MPa，实验采用安全压力内的注入压力进行操作，分别设置入口端压力为550，500，450，400，350，300，250，200，150，120，100，80，60，40 kPa进行测试。由于是低压测试，为了确保实验的准确性，在铜管入口端设置稳压阀（稳流阀），其稳压范围为0～1 MPa，出口端连通大气。

实验中在电子气体流量计后接入皂沫流量计进行校准测试，电子气体流量计与计算机相连，通过计算机准确记录气体流量。高精度（1 kPa）的电子压力传感器也与计算机相连，通过计算机准确记录出、入口端压力数据。

H65-Y型黄铜的布氏硬度为255，由布氏硬度与抗拉强度的经验公式[15]可知造成铜管裂缝变形的最低抗拉强度为1 020 kPa，远大于实验测试中最大入口端压力（550 kPa）。此外，实验后利用精度为0.01 mm的电子游标卡尺测量铜管的缝高，并未发现缝高发生变化，证明铜管不会因注入压力的增加而发生形变。

1.3 实验结果

根据流动测试实验结果绘制压差与流量的关系图（见图4）并添加直线型趋势线，可以发现，各铜管裂缝的压差与流量均存在一定的非线性关系，与流体力学中理想光滑裂缝的哈根-泊肃叶线性流动不同，也与常规的多孔介质达西线性渗流不同。因此，需要对不同开闭程度裂缝中的气体流动状态进行判断。

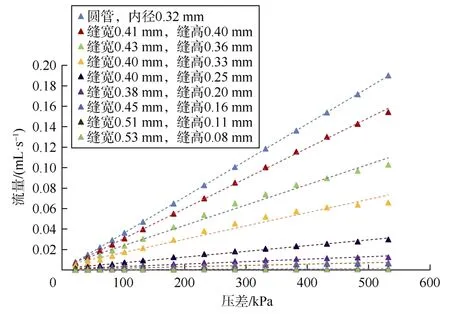
图4 流动测试实验结果

1.3.1 基于Forchheimer方程的流动状态判断

Forchheimer[16]发现了非线性流动现象，提出著名的Forchheimer方程，引入非线性流动系数的概念。Barree等[17]忽略了重力的影响，改写了Forchheimer方程：

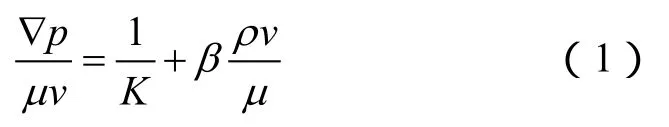
由（1）式可知，非线性流动系数（β）可以通过绘制∇p/μv与ρv/μ的关系曲线（见图5）得到，曲线斜率即非线性流动系数，截距即流动系数（K）的倒数。利用（1）式，可将图4所示流动测试实验结果的线性段与非线性段区分开（见图 6）。可以看出，缝高为0.11～0.40 mm时，随着铜管裂缝缝高和裂缝面积的减小，流动系数降低，非线性流动系数增加（见图 5），线性段减少，非线性段增加（见图6）。而缝高减小到0.08 mm时，流动系数同样降低，但非线性流动系数却没有增加而有所降低（见图5），线性段也有所增加（见图 6）。说明裂缝的流动状态会随着缝高的减小出现转换，可能存在转换界限和转换区间。

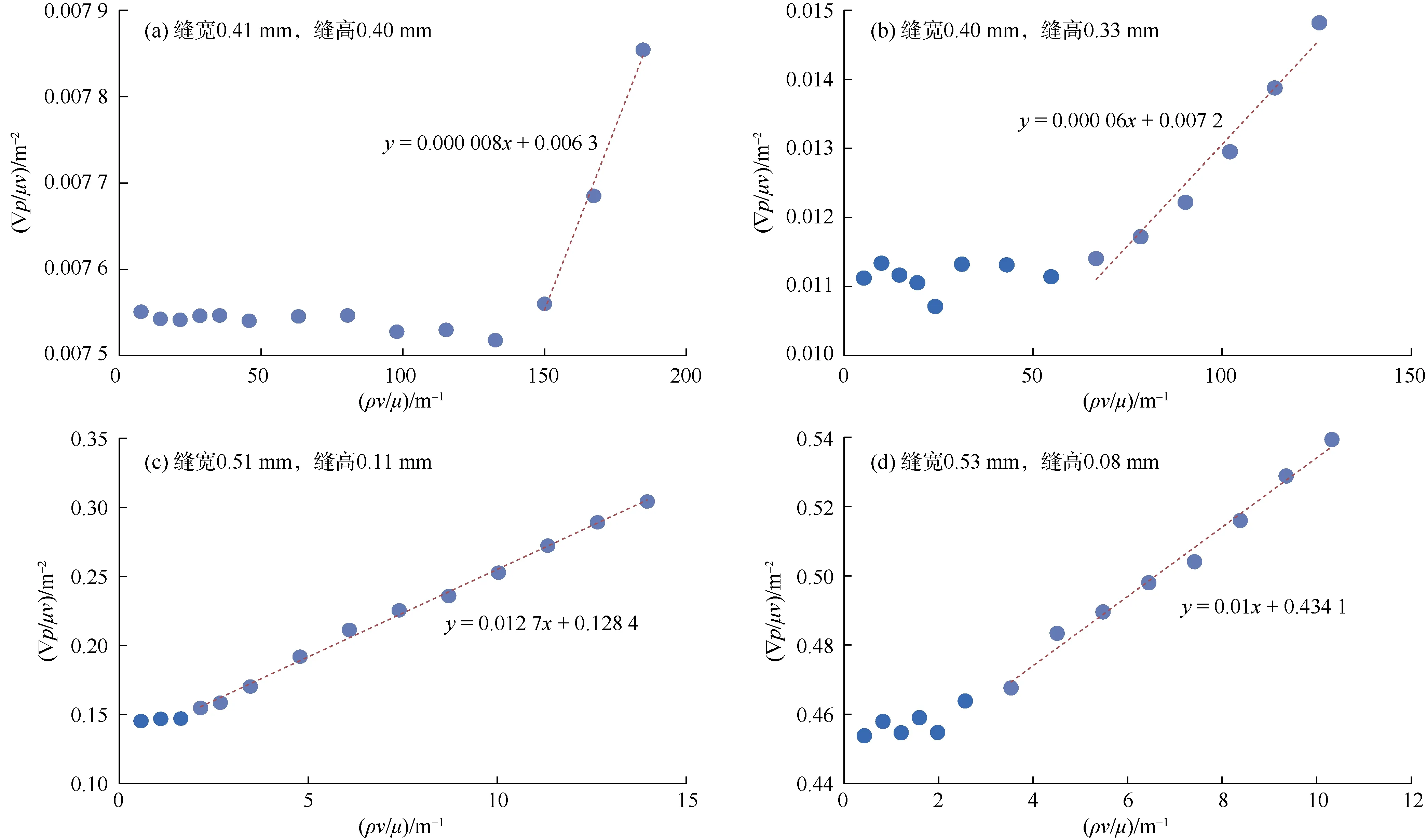
图5 不同开闭程度裂缝的∇p/μv与ρv/μ关系曲线

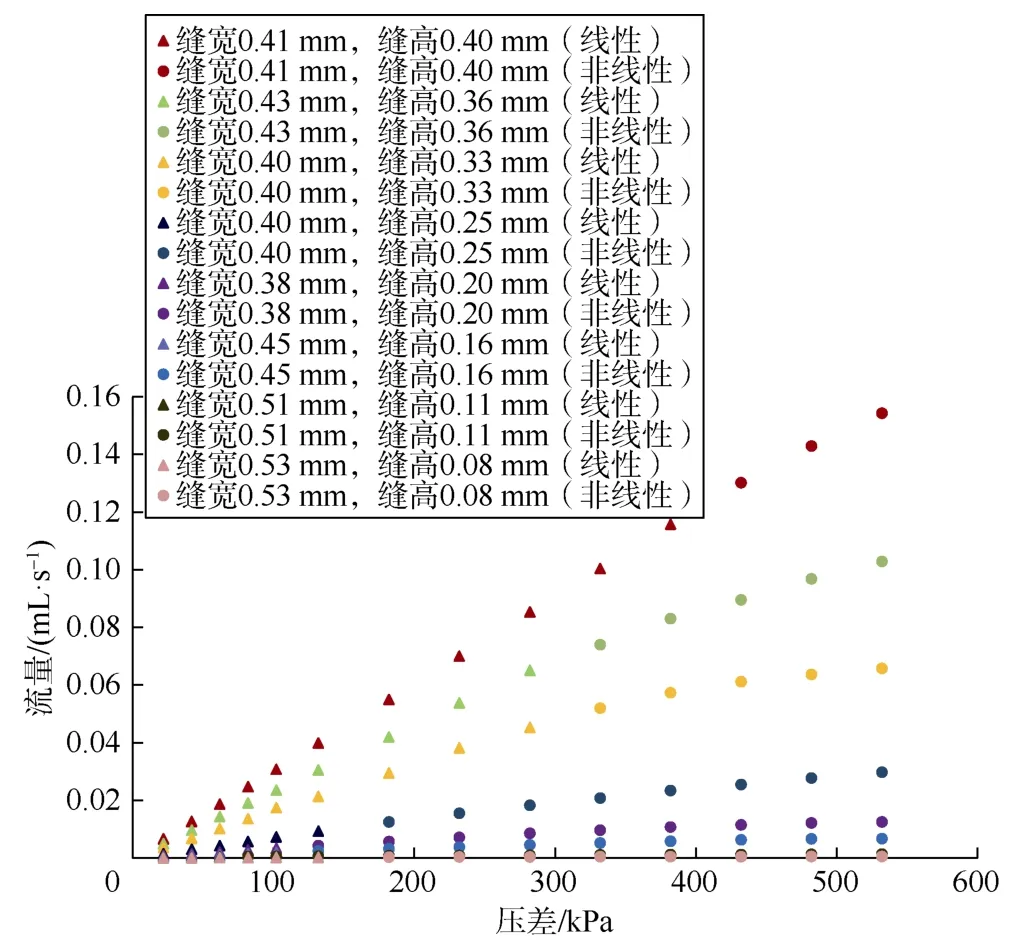
图6 基于Forchheimer方程的线性段与非线性段划分

1.3.2 基于阻力系数-雷诺数关系的流动状态判断

根据黏性流体的雷诺数相似定律，雷诺数相等时流体受黏性力的作用动力相似[18]。在发生线性流动时，流体仅受黏性力或主要受黏性力作用，阻力系数为雷诺数的单变量函数，因此可以根据阻力系数-雷诺数关系来判断流体流动状态[19-20]。考虑到流通系数（ξ）能表征岩石物性，因此采用基于流通系数的雷诺数和阻力系数[19-20]：

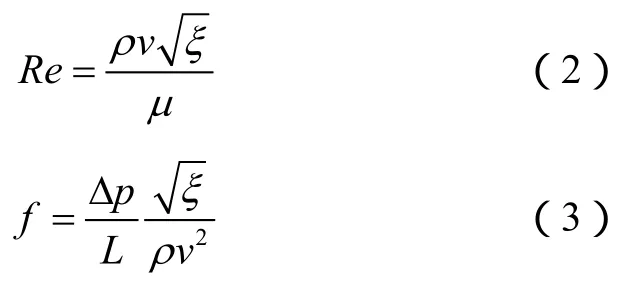
通过绘制阻力系数与雷诺数的关系曲线可以划分裂缝内流动的线性层流区与非线性紊流区，如图 7所示。可以看出，随着铜管裂缝缝高和裂缝面积的减小，雷诺数减小，阻力系数增大，线性层流区逐渐减少，紊流区逐渐增加。

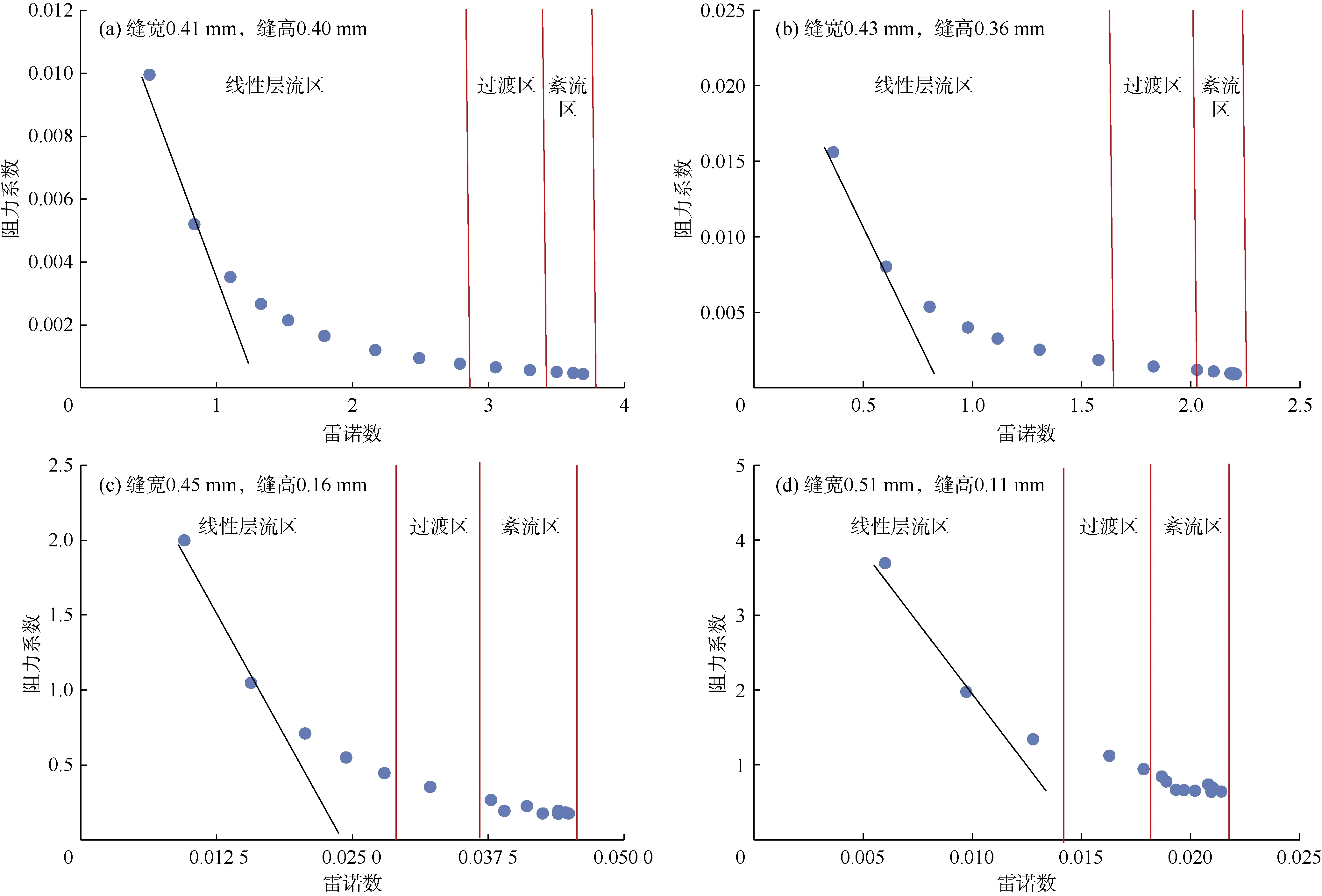
图7 不同开闭程度裂缝的阻力系数-雷诺数关系曲线

根据阻力系数-雷诺数关系，也可将图4所示流动测试实验结果的线性段与非线性段区分开来（见图8）。对比图6与图8可知，基于Forchheimer方程和基于阻力系数-雷诺数关系进行流动状态判断时，线性段与非线性段的划分结果基本一致。因此，可将气体在模拟裂缝中的流动状态分为线性流动和非线性流动。

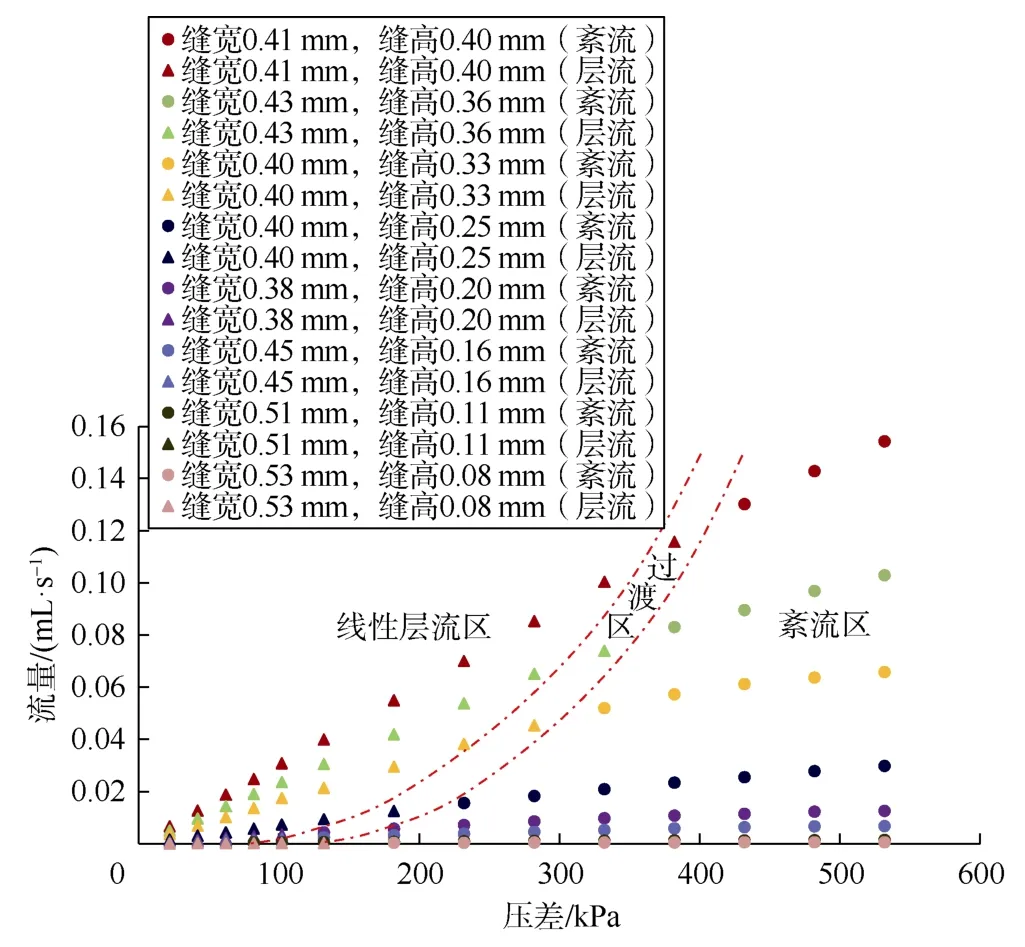
图8 基于雷诺数-阻力系数关系的线性段与非线性段划分

2 基于实验测试结果的流动状态转换界限分析

2.1 流动状态转换界限判断

2.1.1 基于哈根-泊肃叶自由流动法则的判断

理想状态下气体在绝对光滑圆管和裂缝中遵从哈根-泊肃叶的线性流动形式[18]。以基于 Forchheimer方程的划分结果（见图6）为标准，将流动测试实验结果的非线性段去掉，可得到如图9所示流量-压差关系实验值的线性段。基于实验参数采用哈根-泊肃叶方程进行计算，可以得到如图10所示流量-压差关系的泊肃叶理论值。适用于圆管和裂缝的哈根-泊肃叶方程[18]分别如（4）式和（5）式所示。将不同开闭程度裂缝流量-压差关系的泊肃叶理论值与实验值进行比较，分析两者差异及其随缝高的变化趋势，即可判断流动状态转换的缝高界限。

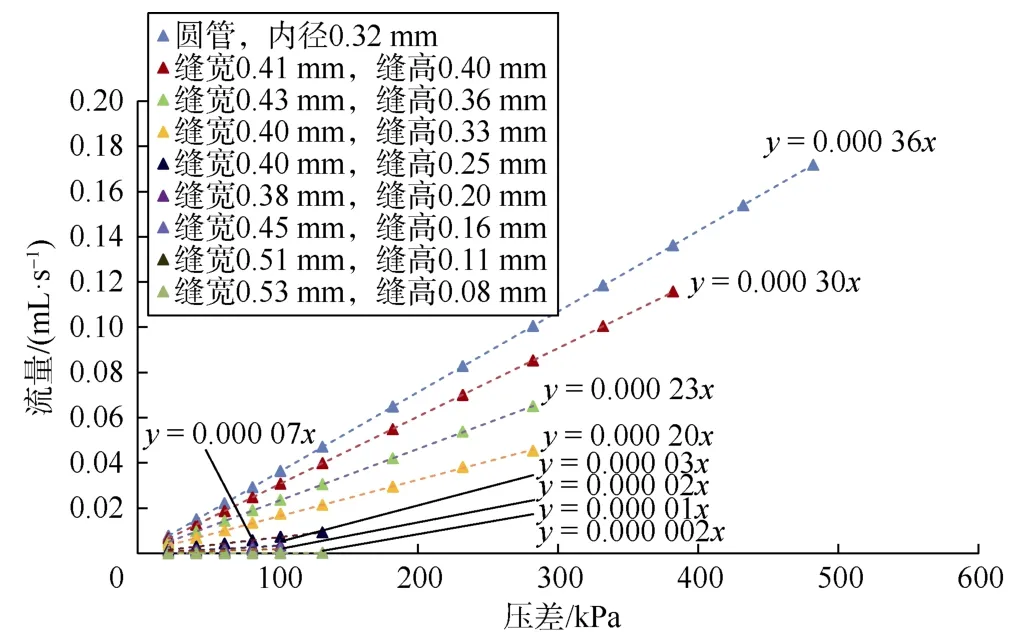
图9 圆管和裂缝中流量-压差关系的实验值线性段

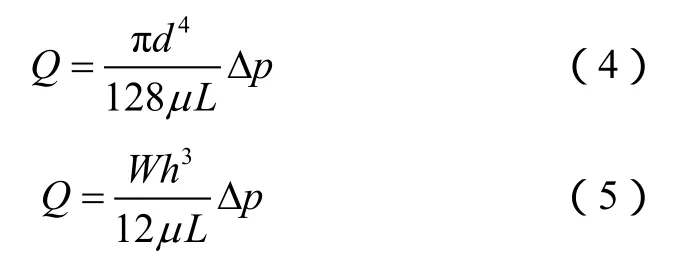
由图 10可知，圆管的哈根-泊肃叶流动与裂缝的哈根-泊肃叶流动有明显差距。本文实验中的圆管内径为0.320 mm，截面积为0.080 mm2，而与其截面积相近的裂缝的气体流动能力都与其有明显差距，例如缝宽0.400 mm、缝高0.250 mm、截面积0.100 mm2的裂缝和缝宽0.380 mm、缝高0.200 mm、截面积0.076 mm2的裂缝。只有缝宽 0.410 mm、缝高 0.400 mm、截面积0.164 mm2的裂缝与圆管的气体流动能力相近。说明圆管的气体流通性远高于相同截面积裂缝的气体流通性。

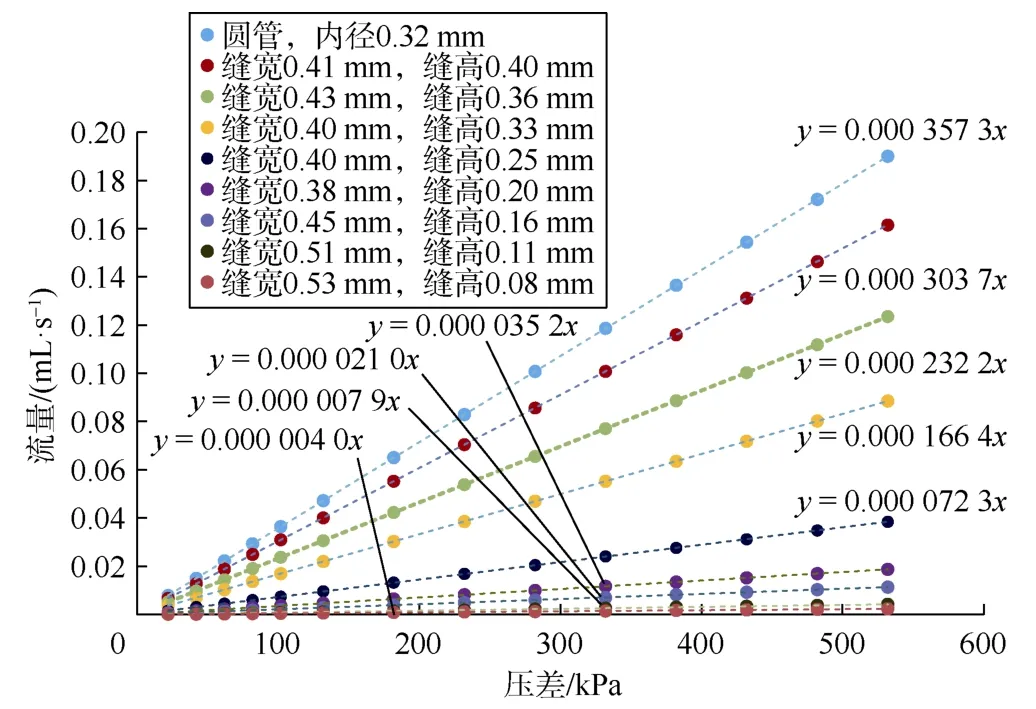
图10 圆管和裂缝中流量-压差关系的泊肃叶理论值

对比不同开闭程度裂缝流量-压差关系的泊肃叶理论值与实验值（见图 11）可以发现，压差与流量泊肃叶理论值呈线性相关，实验值去掉非线性段后在低压差下也为线性直线，但泊肃叶理论值与实验值直线斜率存在差异。将斜率转化为角度，由图12可见，随着缝高的减小，角度差（夹角）越来越大，但当缝高减小到一定值（0.2 mm）后夹角的增幅明显减小，出现一个明显的拐点。初步判断在此拐点后气体在裂缝中的流动形式受微凸体的影响发生了变化，即此拐点为由于缝高的减小气体在裂缝中的流动从以理想光滑缝面的哈根-泊肃叶流动为主向非哈根-泊肃叶流动为主转换的临界点。

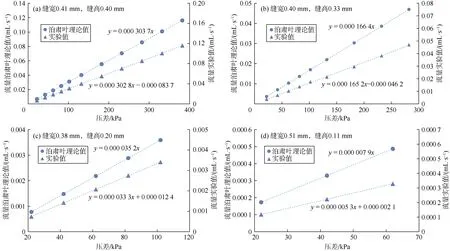
图11 不同开闭程度裂缝流量-压差关系的泊肃叶理论值与实验值对比

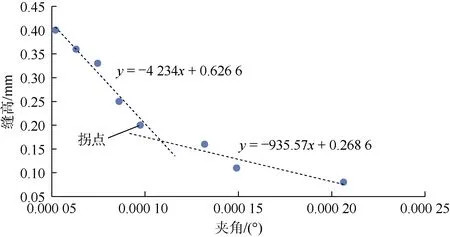
图12 泊肃叶理论值与实验值直线夹角与缝高关系

2.1.2 基于幂律方程-渗流法则的判断

采用目前在渗流中应用较为广泛的幂律方程（见（6）式）[20]，从渗流的角度进一步界定铜管裂缝中流动状态的转换[20-21]，并与填砂铜管比较。

基于（6）式进行幂指数回归拟合可得到各铜管裂缝的平衡系数（α）和非线性流动指数（m）（见图13）。如果不区分线性段和非线性段，对于铜管裂缝，缝高为0.11～0.40 mm时，m值随缝高的减小而减小，非线性流动加剧，而当缝高继续减小到0.08 mm时，m值增大，非线性流动减弱。对于填砂铜管，m值随填砂颗粒粒径的减小而增大。显然铜管裂缝m值的大小与微凸体的接触、咬合程度直接相关。对于线性流动，m值为1，将此时的幂律方程代入渗流方程（见（7）式）可知，平衡系数（α）与渗流系数（ξ/μ）相等。因此，将不同开闭程度裂缝平衡系数与渗流系数进行比较，分析两者差异及其随缝高的变化趋势，即可判断流动状态转换的缝高界限。

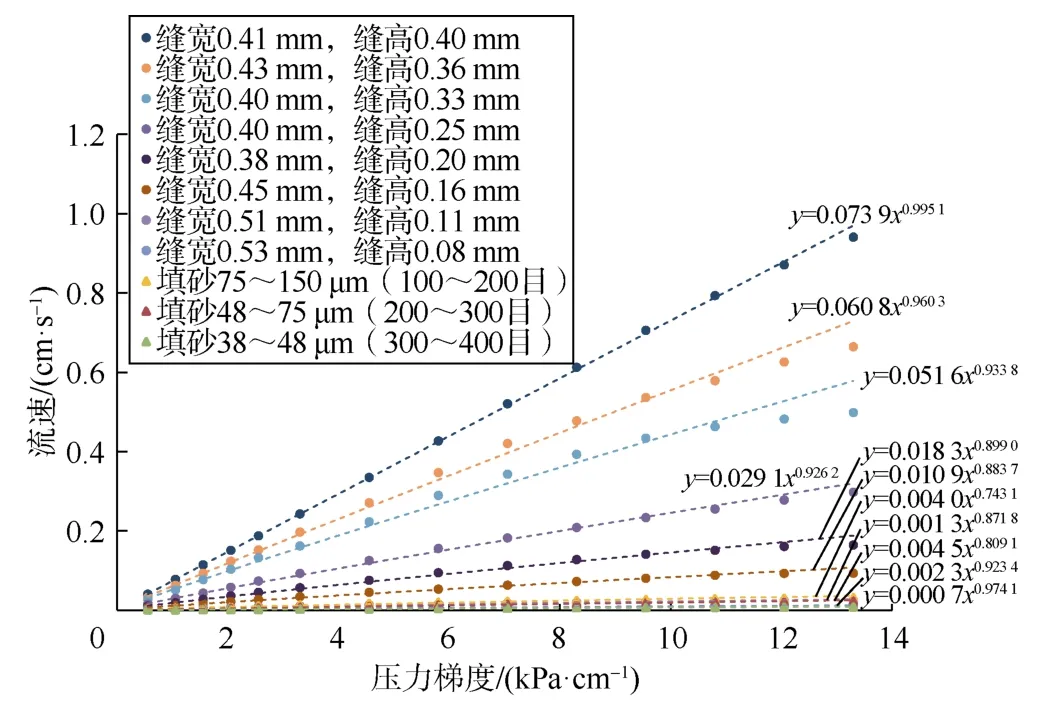
图13 低速渗流实验压力梯度与流速的幂律关系

根据前文中流动状态判断结果，截取图13中的线性段，此时 m值约等于 1，如图 14所示。结合图 14及（7）式可计算得到各铜管裂缝的渗流系数（ξ/μ）。将不同缝高下渗流系数与平衡系数间偏差进行对比（见图15）可以发现，偏差值的趋势线在缝高0.2 mm前后明显不同，说明在缝高0.2 mm前后气体的流动状态发生了明显变化。

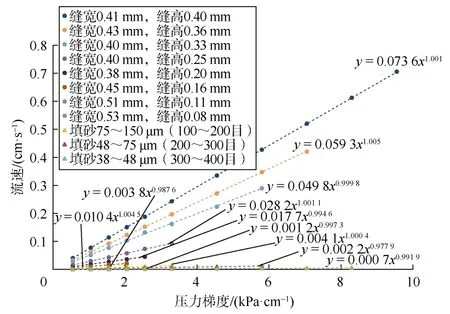
图14 低速渗流实验压力梯度与流速线性段幂律关系

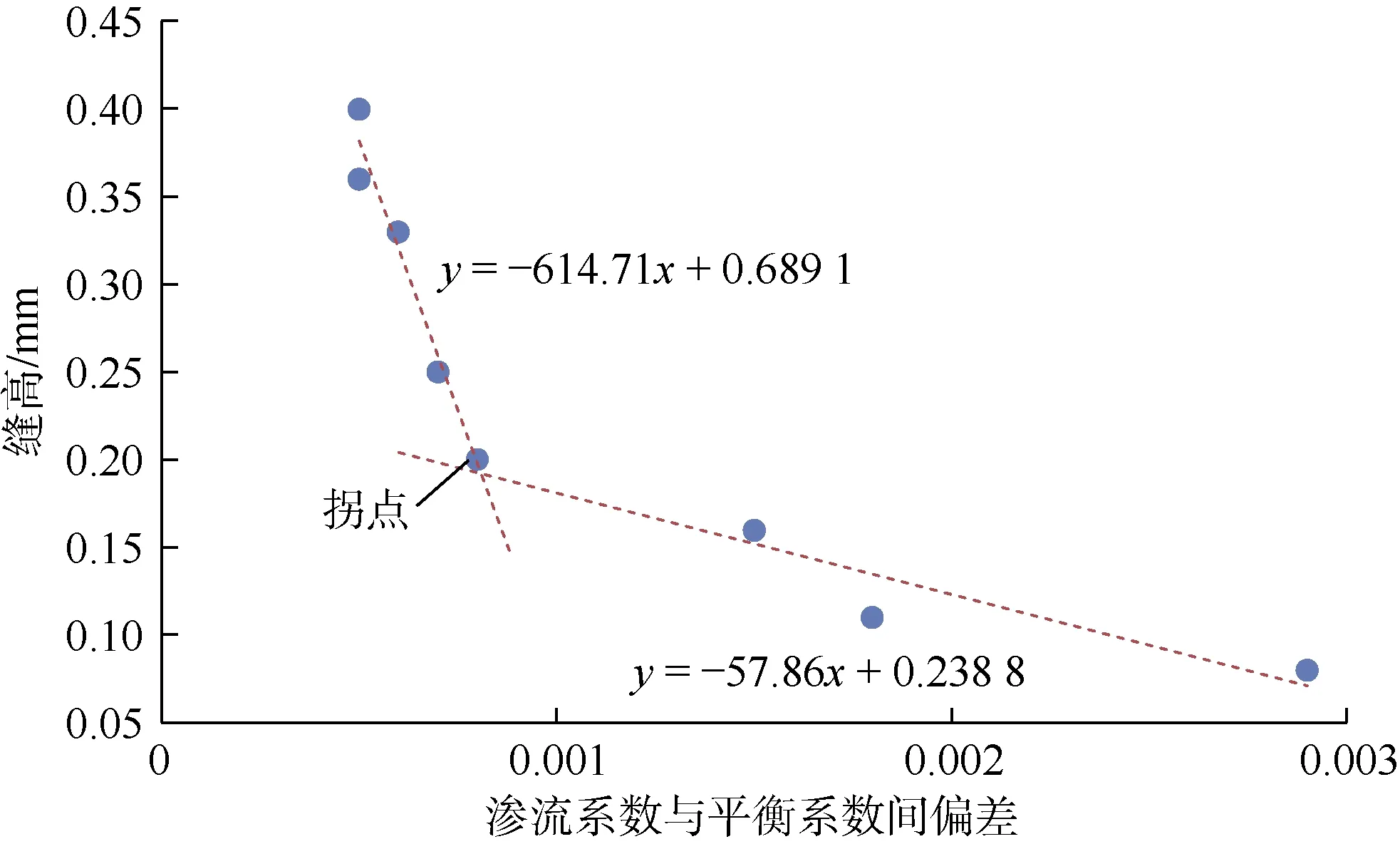
图15 渗流系数、平衡系数间偏差与缝高的关系曲线

综合上述两种判断方式可以确定本文中铜管裂缝流动状态转换的缝高界限为 0.2 mm，在缝高减小到0.2 mm 后流动状态由以哈根-泊肃叶流动为主向非哈根-泊肃叶流动为主转换。

2.2 流动状态转换区间确定

由图16可知，与缝高大于0.08 mm时的趋势不同，缝高减小到0.08 mm时，压力梯度与流速关系曲线的线性段不再随着缝高的减小而减少，而是有所增加，说明流动形式再次发生了转变。这与前文分析结果一致。

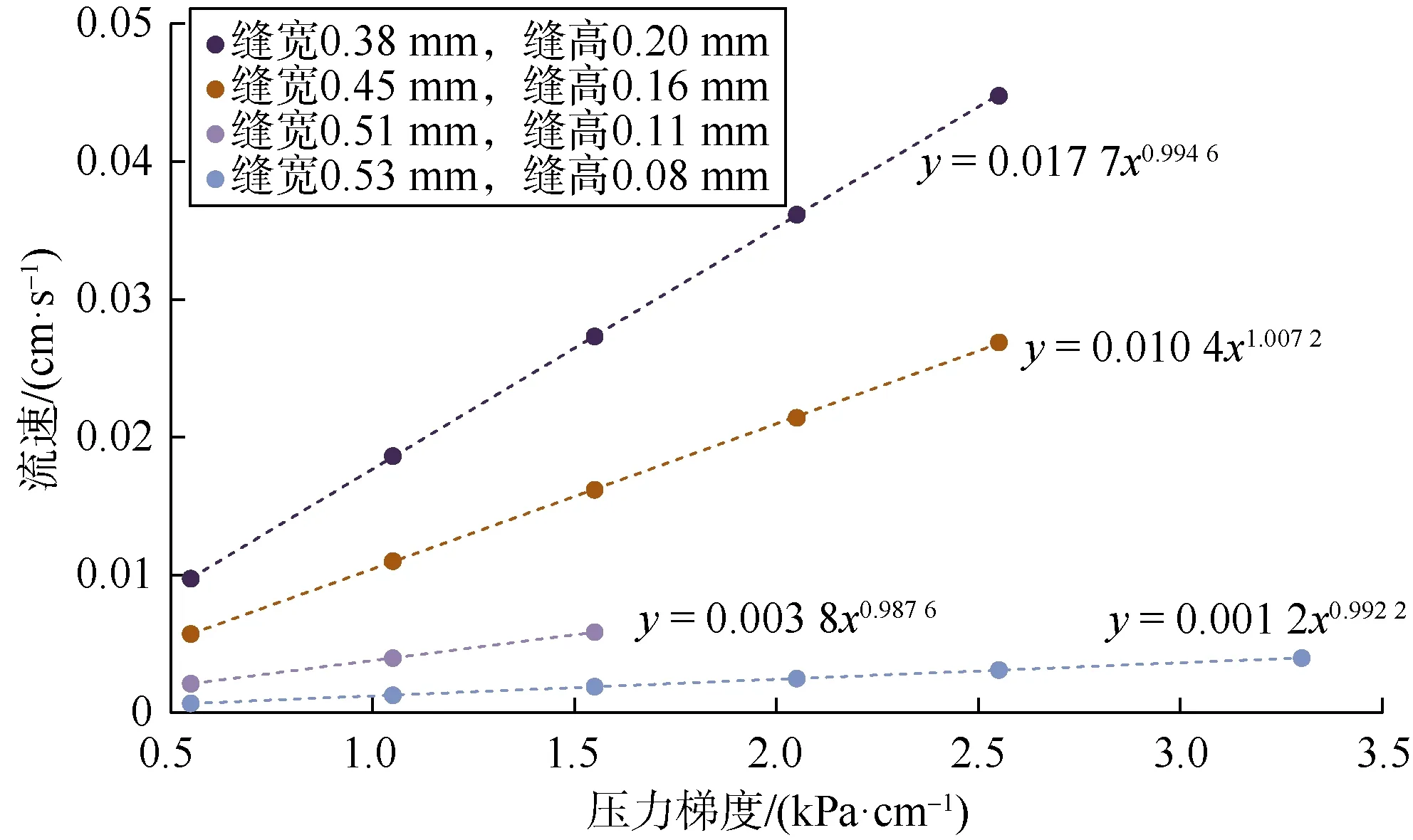
图16 低速渗流实验压力梯度与流速关系曲线线性段

将铜管裂缝与填砂铜管的压力梯度与流速关系曲线线性段进行对比（见图17）可以发现，缝高为0.08 mm的铜管裂缝与填砂38～48 μm（300～400目）的铜管的线性段相近。用饱和煤油法测量铜管裂缝及填砂铜管的孔隙度进行对比可以发现，缝高为0.08 mm的铜管裂缝的孔隙度为21%，与填砂38～48 μm（300～400目）的铜管的孔隙度（17%）相近。因此，可以确定缝高减小到0.08 mm时铜管裂缝中微凸体已经咬合形成较为理想的多孔介质，流动形式转变为达西渗流。

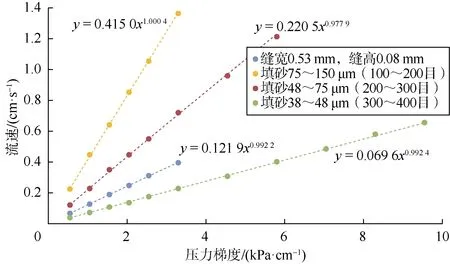
图17 铜管裂缝、填砂铜管压力梯度与流速关系曲线线性段对比

综合前文所述，裂缝缝高减小到一定程度后，微凸体接触、咬合，形成了较为复杂的多孔介质，且孔隙分布逐渐均匀，从而线性流动增加，逐渐向理想的达西流动转化。可以确定本文中铜管裂缝的流动状态由以哈根泊肃叶流动为主转换为达西流动的缝高区间为0.08～0.20 mm。

3 流动状态转换界限计算方法

3.1 边界层对流动状态转换界限的影响

黏性气体在裂缝中流动时，在裂缝壁面存在一薄层，即边界层[18]。为了明确裂缝中微凸体的咬合程度与流动状态转换的关系，需首先明确边界层厚度对流动状态转换界限的影响程度。

边界层分为层流边界层和紊流边界层[17]，在裂缝通道中存在边界层流态转变距离，且对于平行裂缝而言，层流边界层转变为紊流边界层的雷诺数区间为5×105～3×106。取临界雷诺数 5×105，计算得到边界层流态转变点与裂缝前缘最短距离为7.0 m，而本文实验测试所用超细铜管裂缝长度为0.4 m，因此可以确定实验中边界层为层流边界层。从而可以计算得到各压力梯度下不同尺度铜管裂缝的边界层厚度（见图18），可以看出，在缝高0.2 mm（流动状态转换界限）的铜管裂缝中，最大边界层厚度约为0.6 μm，即边界层厚度对流动状态转换界限的影响极小，可忽略。

图18 边界层厚度与压力梯度关系

3.2 三维微凸体扫描

采用白光干涉仪扫描得到铜管裂缝内表面的三维形貌特征[22]，根据测量的微凸体高度综合分析得到铜管裂缝的流动状态转换界限，初步建立裂缝的流动状态转换界限计算方法。

根据白光干涉仪三维图形扫描的统计结果（见图19），将扫描结果的基线进行归零化处理，得到铜管裂缝的微凸体高度在0～57 μm，而缝高0.2 mm（流动状态转换界限）的铜管裂缝中最大边界层厚度约为0.6 μm，说明边界层对微凸体咬合关系的影响极小，对测试结果的影响可以忽略。假设裂缝上下两面相同，则裂缝上下两面的最大微凸体高度之和为114 μm，而流动状态转换缝高界限为0.2 mm，即200 μm，那么铜管裂缝内的最大微凸体高度与流动状态转换缝高界限的一半相接近。而对于缝高小于0.2 mm的裂缝，气体在裂缝中的流动受到微凸体的影响愈加明显，且在缝高小于最大微凸体高度后，微凸体逐渐接触、咬合，裂缝通道逐渐转变为多孔介质。

3.3 流动状态转换界限的计算

本文实验中铜管裂缝的单面微凸体高度在0～57 μm，根据统计学结果（见图 19），微凸体高度服从高斯分布[23]，即：

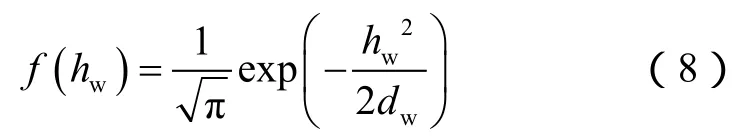
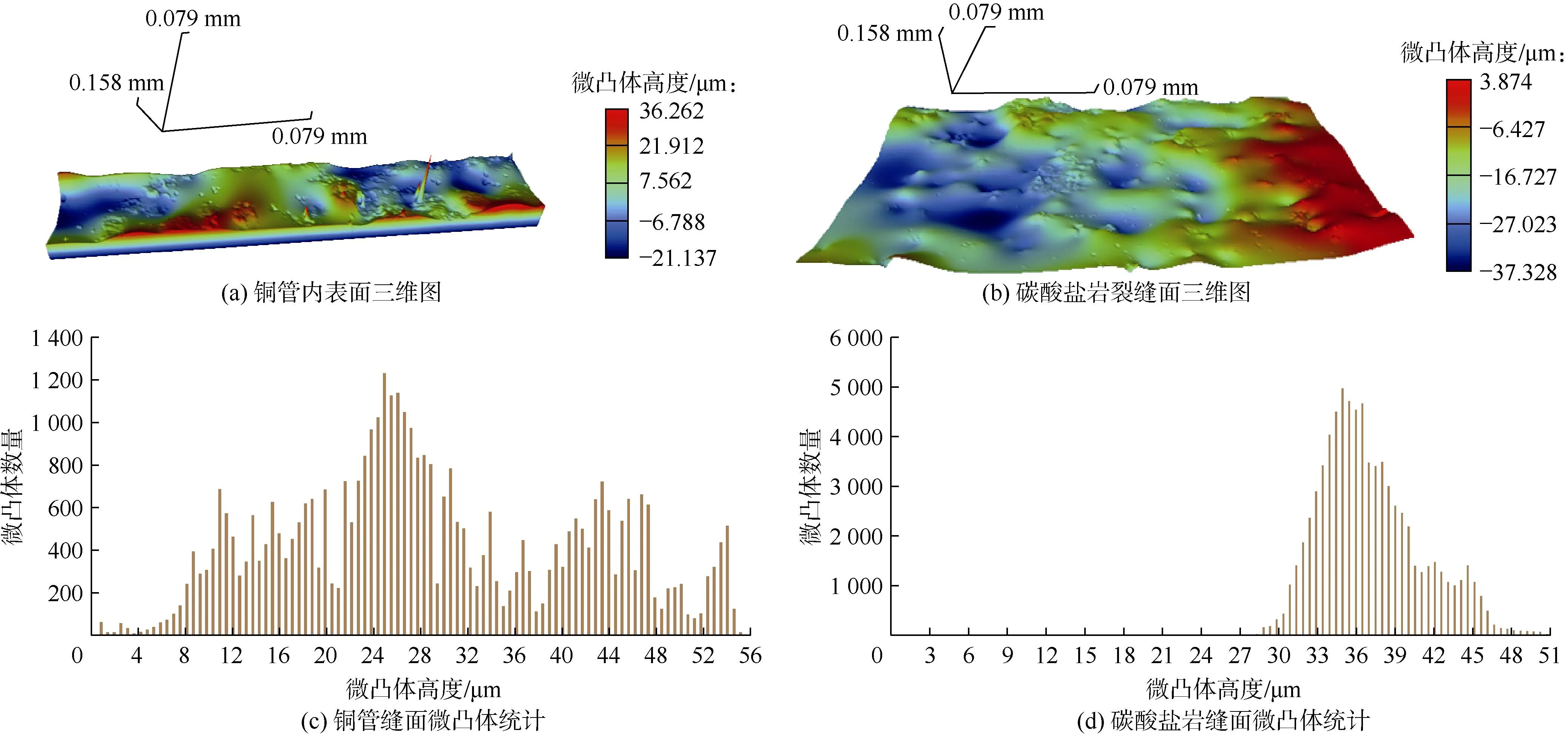
图19 三维扫描测试结果

由于裂缝面微凸体高度为高斯分布，且具有起伏特性，适合运用分形理论来进行粗糙度系数的计算。本文引用张国彪等[24]建立的函数关系，利用分形维数计算粗糙度系数。已知实验采用的铜管为H65-Y型，并查得该铜管的弹性模量为120 GPa，泊松比为0.34，布氏硬度为255[25]。分形维数的计算式为：

则粗糙度系数计算式为：

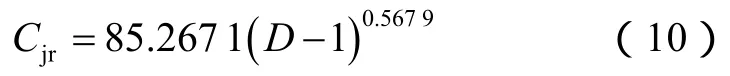
由于实验采用的是气体流动测试，所以流动状态转换界限必然与气体自身的性质相关，而气体在裂缝中微凸体间的流动能力必然与气体黏度直接相关。综合粗糙度系数、气体黏度及裂缝材料自身参数，可初步推断流动状态转换缝高界限的表达式为：

（11）式中，c为材料的压缩系数[25]，计算式为：

根据计算得到的铜管裂缝各参数（见表1）以及气体黏度 0.018 mPa·s，由（12）式计算得到其流动状态转换缝高界限为0.196 1 mm，与流动实验测试得到的0.2 mm相近，说明建立的理论计算方法可行。

表1 铜管裂缝各参数计算结果统计

根据图19中实际地层碳酸盐岩裂缝面三维扫描结果同样可计算对应流动状态转换缝高界限。该碳酸盐岩为白云岩，白云岩的弹性模量为94 GPa，泊松比为0.15，布氏硬度为120。计算得到的碳酸盐岩裂缝各参数如表 2所示，由（12）式计算得到其流动状态转换缝高界限为0.183 7 mm。这与硬度、粗糙度系数降低后相应的缝高界限也应降低的认识是一致的，印证了缝高界限计算方法的合理性。

表2 碳酸盐岩裂缝各参数计算结果统计

为进一步分析本文所建立的理论计算方法的适用性，用文献数据进行了计算分析。文献[26]中超深层裂缝型碳酸盐岩的力学特性参数如表 3所示，对其三维图形基准面归零化处理后得到最大微凸体高度约为1 200 μm，平均高度约为500 μm。文献中给出莫氏硬度为 1.89，结合莫氏硬度与布氏硬度的转换公式，计算得到布式硬度为153。由（12）式计算得到流动状态转换缝高界限为为4.73 mm。

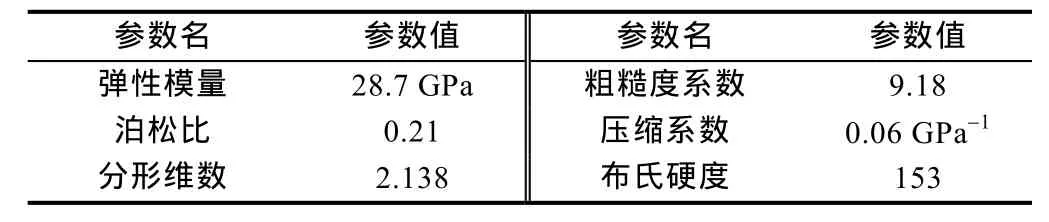
表3 超深层裂缝型碳酸盐岩力学特性[26]

与铜管裂缝和白云岩裂缝相比，文献[26]中超深层裂缝型碳酸盐岩裂缝的缝高界限计算结果较大。假设裂缝上下两面相同，则文献[26]中超深层裂缝型碳酸盐岩裂缝的上下两面的最大微凸体高度为2 400 μm，即2.40 mm，与缝高界限（4.73 mm）的一半相接近，与铜管裂缝测试结果一致，进一步说明本文缝高界限计算方法合理、可行。

4 结论

由于铜管内表面与实际碳酸盐岩裂缝面在微观形貌、对气体分子吸引力及微凸体高度等方面均具有相似性，实验采用超细铜管模拟裂缝是合理的。

将不同开闭程度裂缝流量-压差关系的泊肃叶理论值与实验值作趋势线对比两者斜率差异，两条趋势线间夹角随缝高变化曲线上会出现一个拐点。通过对比幂律方程中的平衡系数及渗流方程中的渗流系数也可以找到这一拐点。该拐点为由于缝高的减小气体在裂缝中的流动从以理想光滑缝面的哈根-泊肃叶流动为主向非哈根-泊肃叶流动为主转换的临界点，即流动状态转换界限。裂缝缝高在流动状态转换缝高界限以下继续减小到一定程度后，微凸体接触、咬合，形成较为复杂的多孔介质，且孔隙分布逐渐均匀，从而线性流动增加，逐渐向理想的达西流动转换。从而可以确定裂缝在闭合过程中整个流动状态的转换区间。

气体在裂缝的闭合过程中一共有 3种流动形式，①在缝高较大的裂缝中以哈根-泊肃叶流动为主；②当裂缝缝高受到外力的作用减小至流动状态转换界限时，由以哈根-泊肃叶流动为主向以达西流动为主转换，且存在一个转换区间；③当裂缝缝高继续减小至超出转换区间以后，流动形式完全转变为达西流动。

综合裂缝面的三维微凸体扫描结果、裂缝的材料性质及流体性质，建立了流动状态转换界限计算方法。实验测试和理论计算表明，从管流到达西流的缝高界限约为裂缝上、下两面微凸体最大高度之和的2倍。

符号注释：