全球探空站附近掩星观测资料误差估计
2022-07-14王明明邹晓蕾徐徐
王明明 邹晓蕾 徐徐
(南京信息工程大学 资料同化和应用中心,南京210044)
引 言
全球定位系统(Global Positioning System,GPS)自问世以来,不仅在导航和定位领域体现了其优越性,在大气海洋及空间环境探测领域也应用广泛[1]。自1995年GPS无线电掩星(Radio Occultation,RO)技术首次应用于地球大气探测以来[2],许多掩星观测任务已经开展,主要包括美国的GPS/MET(GPS/Meteorology)、中国台湾和美国的气象电离层与气象星座观测系统(Constellation Observing System for Meteorology Ionosphere and Climate,COSMIC)、欧洲气象应用卫星MetOp-A/B(Meteorological Operational Satellite)搭载的全球定位系统大气探测接收仪(Global Navigation Satellite System Receiver for Atmospheric Sounding,GRAS)[3-5]。其中,MetOp-A/B星上的GRAS接收器每天可提供约1 300根掩星廓线,较均匀地分布于全球。从FY-3C卫星开始,我国风云系列极轨气象卫星开始搭载全球导航卫星掩星探测仪(Global Navigation Satelite System Occultation Sounder,GNOS),并且所提供的掩星数据已经在我国GRAPES业务系统中应用。目前掩星数据占GRAPES_GFS业务所用观测资料总量的2.1%[6]。
掩星观测资料具有高精度、高垂直分辨率、长期稳定性和不受天气现象影响的特点[7],在数值天气预报中可以作为卫星微波和红外观测的补充。已有研究[8]表明,同化掩星观测资料可以改善数值天气预报的结果。对于变分资料同化,观测误差方差是必要的输入参数,在许多变分资料同化方案中,以观测误差方差的倒数来对观测数据进行加权[9-10],这意味着掩星资料的观测误差会直接影响掩星资料同化的结果。
关于估算GPS掩星资料的观测误差,前人已进行了许多研究。SHAO, et al[9]使用掩星观测资料和美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)预报场之差来估计掩星观测误差方差,并且分析了使用不同观测资料权重对掩星弯角资料同化的影响。Desroziers, et al[11]和CHEN, et al[12]在假设观测误差与预报误差不相关的条件下,使用表观误差(即观测场减去背景场,O-B)方差减去预报误差方差作为观测误差方差。这种方法估计观测误差需要借助模式预报得到预报误差。Anthes, et al[13]首次将“三角帽”方法应用于掩星观测资料误差估计,使用掩星观测、探空(Radiosonde,RS)观测、欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)ERA-Interim再分析资料和NCEP全球预报分析数据(Global Forecast System,GFS)4种资料的不同组合来估计掩星折射率资料的观测误差方差。该方法不需要使用模式估计预报误差,且能够估算得到与前人方法结果相近的观测误差。XU, et al[14]采用“三角帽”法,使用掩星、探空观测、美国GFS分析资料和欧洲ERA-Interim再分析资料4种数据,对掩星和探空观测资料进行质量控制后,估计了中国境内48个探空站以及西北太平洋6°×6°经纬度网格点附近的掩星折射率和弯角的观测误差,揭示了掩星观测误差的纬度依赖性以及一定的海陆差异。
使用“三角帽”方法估计观测误差的一个前提假设是使用的资料集的误差互不相关。前人研究中使用的ERA-Interim再分析资料同化了掩星和探空观测资料[13],这3种资料集的误差相关性对估算结果存在明显影响[15-16]。因此,本研究引入一种垂直和水平分辨率较高的独立数据:美国微波综合反演系统(Microwave Integrated Retrieval System,MiRS)卫星微波资料反演产品,替换ERA-Interim数据,以避免数据集之间的误差相关性对结果的影响。同时也研究了未替换ERA-Interim数据估算的结果,以便与前人研究进行比较。由于ERA-Interim数据在2019年8月31日停止发布,本研究使用水平分辨率更高(0.25°×0.25°)的ERA5数据,且扩展了数据时间范围(2016年1月1日至2020年10月1日),估算了全球范围内筛选出的471个探空站点附近掩星折射率和弯角资料的观测误差标准差。
1 数据介绍
本研究共使用5种数据集,即掩星观测、探空观测、ERA5再分析资料、GFS分析资料和MiRS卫星微波资料反演产品,使用的时间范围为2016年1月1日至2020年10月1日。将这5种数据集进行不同的组合估算GPS掩星折射率和弯角资料的观测误差标准差。资料组合一:RO、RS、ERA5、GFS;资料组合二:RO、RS、GFS、MiRS;资料组合三:RO、RS、ERA5、MiRS。由于本次研究主要关注对流层和水汽的影响,因此结果展示的垂直范围为200~1 000 hPa或影响高度2~14 km。
1.1 掩星资料
本研究使用了COSMIC资料分析与归档中心CDAAC(COSMIC data analysis and archive center)提供的MetOp-A/B星GRAS接收器得到的掩星资料。CDAAC提供掩星弯角廓线资料“atmPrf”和一维变分(1D-Var)反演的湿大气状态廓线“wetPrf”,前者包含观测弯角、折射率、干大气状态反演的气压和温度,垂直分辨率为20 m,“wetPrf”包含折射率、湿大气状态下反演的气压、温度和水汽压,垂直分辨率为100 m。本文主要使用掩星弯角、折射率和湿大气状态下反演的温度和水汽压。
1.2 MiRS卫星反演产品
美国MiRS卫星反演产品采用一维变分反演算法,以快速辐射传输模式CRTM作为前向算子和伴随算子[17-18],将极轨卫星微波、红外等观测资料反演为大气温度、湿度变量。该系统是由美国海洋与大气管理局(NOAA)/国家环境卫星数据和信息服务中心(NESDIS)的卫星应用研究中心(STAR)开发的,是对现有的微波地表和降水产品MSPPS的重大升级。
本文选用NOAA-18、NOAA-19和MetOp-A卫星上微波温度探测计AMSU-A和微波湿度探测计MHS数据的MiRS反演产品,使用了其温度、气压和水汽压这3个变量。图1展示了2016年1月1日MetOp-A卫星AMSU-A观测在4个不同时间段内的扫描带边缘位置、MiRS反演的500 hPa全球温度分布和500 hPa高度MiRS反演温度与ERA5温度的差值。由于MiRS反演产品中不包含折射率这一变量,因此折射率由以下公式计算得到:
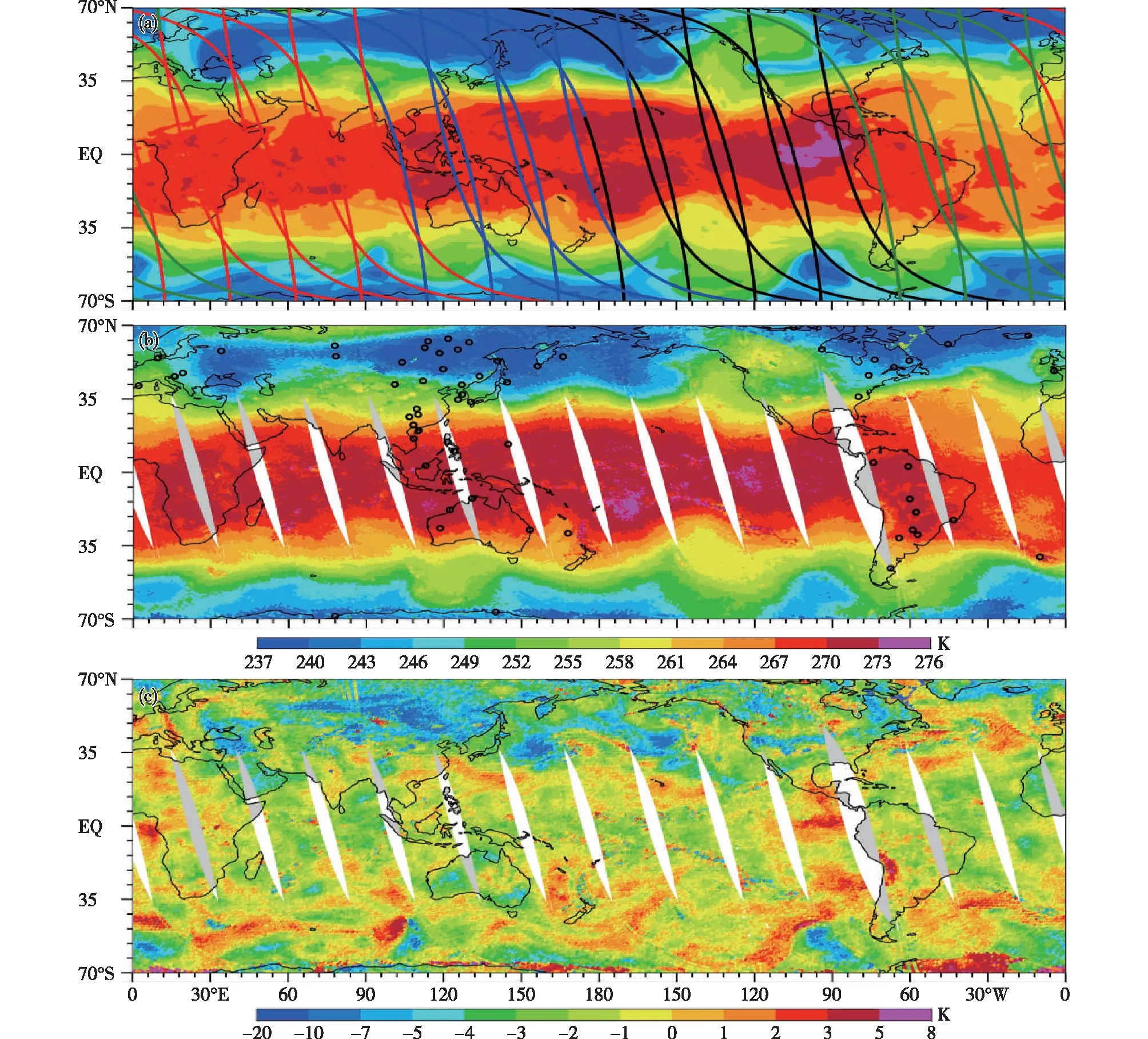
图1 2016年1月1日(a)06时ERA5数据,(b)03时至次日03时MiRS反演MetOp-A卫星资料得到的全球500 hPa温度和(c)ERA5数据与ERA5数据±3 h时刻内MiRS反演温度之差;a中实线表示MetOp-A卫星AMSU-A仪器在06时(黑)、12时(蓝)、18时(红)和24时(绿)±3 h的扫描带边缘;b中黑色空心圈表示06时匹配到掩星廓线的探空站点位置
。
(1)
其中:N表示折射率;P表示气压(单位:hPa);T表示温度(单位:K);e表示水汽压(单位:hPa)。
1.3 ERA5再分析数据
ERA5是欧洲中心ECMWF全球大气第五代再分析数据集。本研究使ERA5再分析数据在空间和时间线性插值到掩星廓线上的数据。图2、3展示了2016年1月1日06时与全球471个探空站观测资料匹配到的(匹配方法见2.1小节)MiRS反演产品、ERA5数据和GPS掩星廓线在垂直方向上的温度分布,MiRS反演产品和ERA5的温度数据之差的垂直分布以及GPS掩星廓线和ERA5的温度数据之差的垂直分布。MiRS反演产品和ERA5的温度数据在中高纬地区(30°~90°N和30°~90°S)存在10 K以内的差值(少数廓线超过10 K),在低纬度地区差值小于5 K。GPS掩星廓线和ERA5的温度数据的差值都在5 K以内。
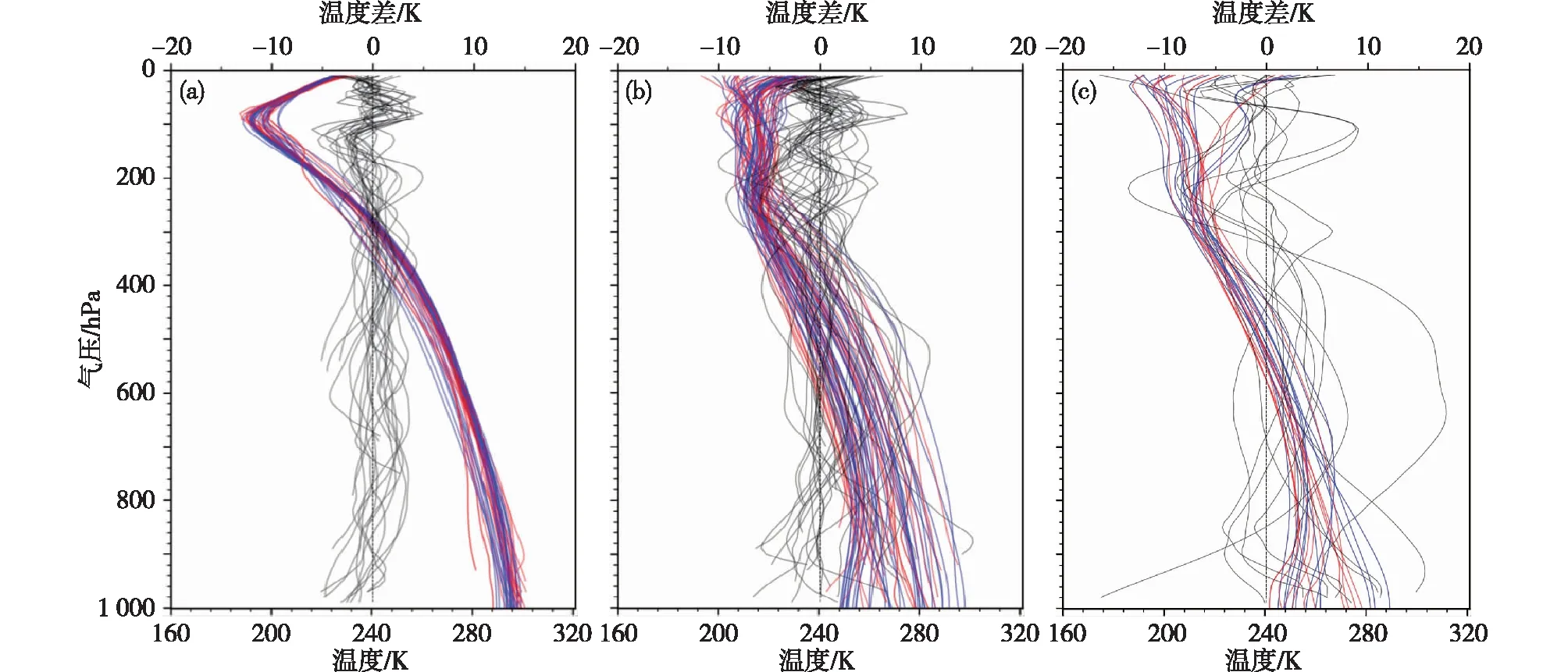
图2 2016年1月1日06时匹配到的(a)低纬(30°S~30°N)、(b)中纬(30°~60°S和30°~60°N)和(c)高纬(60°~90°S和60°~90°N)的MiRS(蓝色)和ERA5(红色)温度的垂直分布(实线)以及两者之差(虚线,上x轴)
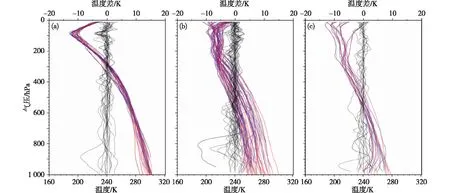
图3 2016年1月1日06时匹配到的(a)低纬(30°S~30°N)、(b)中纬(30°~60°S和30°~60°N)和(c)高纬(60°~90°S和60°~90°N) GPS掩星廓线(蓝色)和ERA5(红色)温度的垂直分布(实线)以及两者之差(虚线,上x轴)
1.4 GFS分析数据
GFS预报分析数据是美国NCEP提供的天气预报分析数据集,包括温度、降水、风、土壤湿度和大气臭氧浓度。本研究使用GFS分析数据在空间和时间上线性插值到掩星廓线的数据。图4展示了2016年1月1日06时全球471个探空站观测资料匹配到的MiRS反演产品和GFS数据温度在垂直方向上的分布和差值。MiRS反演产品和GFS的温度数据在中高纬地区(30°~90°N和30°~90°S)存在10 K以内的差值(少数廓线超过10 K),在低纬度地区差值小于5 K,这与MiRS反演产品和ERA5的温度数据的差值类似。
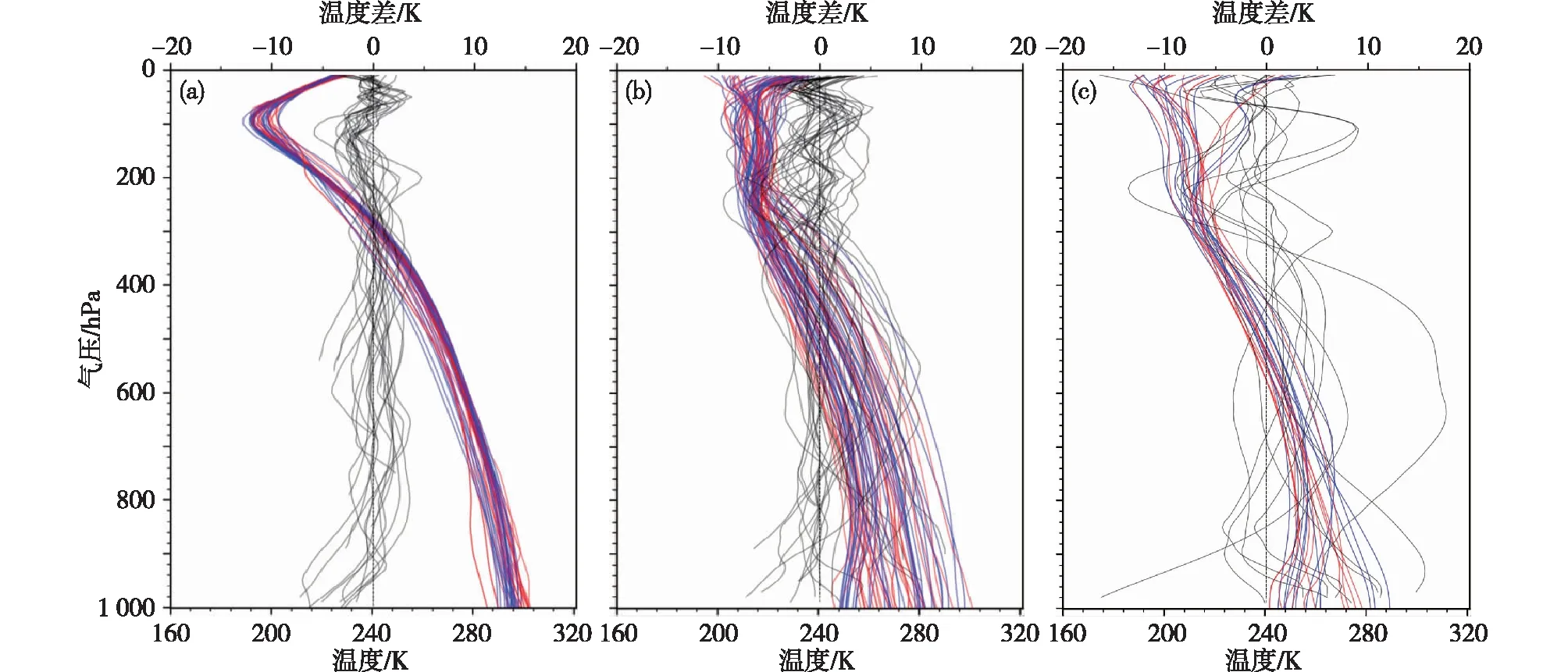
图4 2016年1月1日06时匹配到的(a)低纬(30°S~30°N)、(b)中纬(30°~60°S和30°~60°N)和(c)高纬(60°~90°S和60°~90°N) MiRS(蓝色)和GFS(红色)温度的垂直分布(实线)以及两者之差(虚线,上x轴)
1.5 RS探空数据
本研究使用的探空观测数据来自美国NCEP发布的全球无线电探空数据集。这里对全球探空站点进行了筛选,选出其中300 km范围内无其他站点的471个探空站进行后续的计算与分析。图5a展示了这471个探空站在全球范围内的地理分布。欧亚大陆东岸探空站数量明显多于大陆西岸。
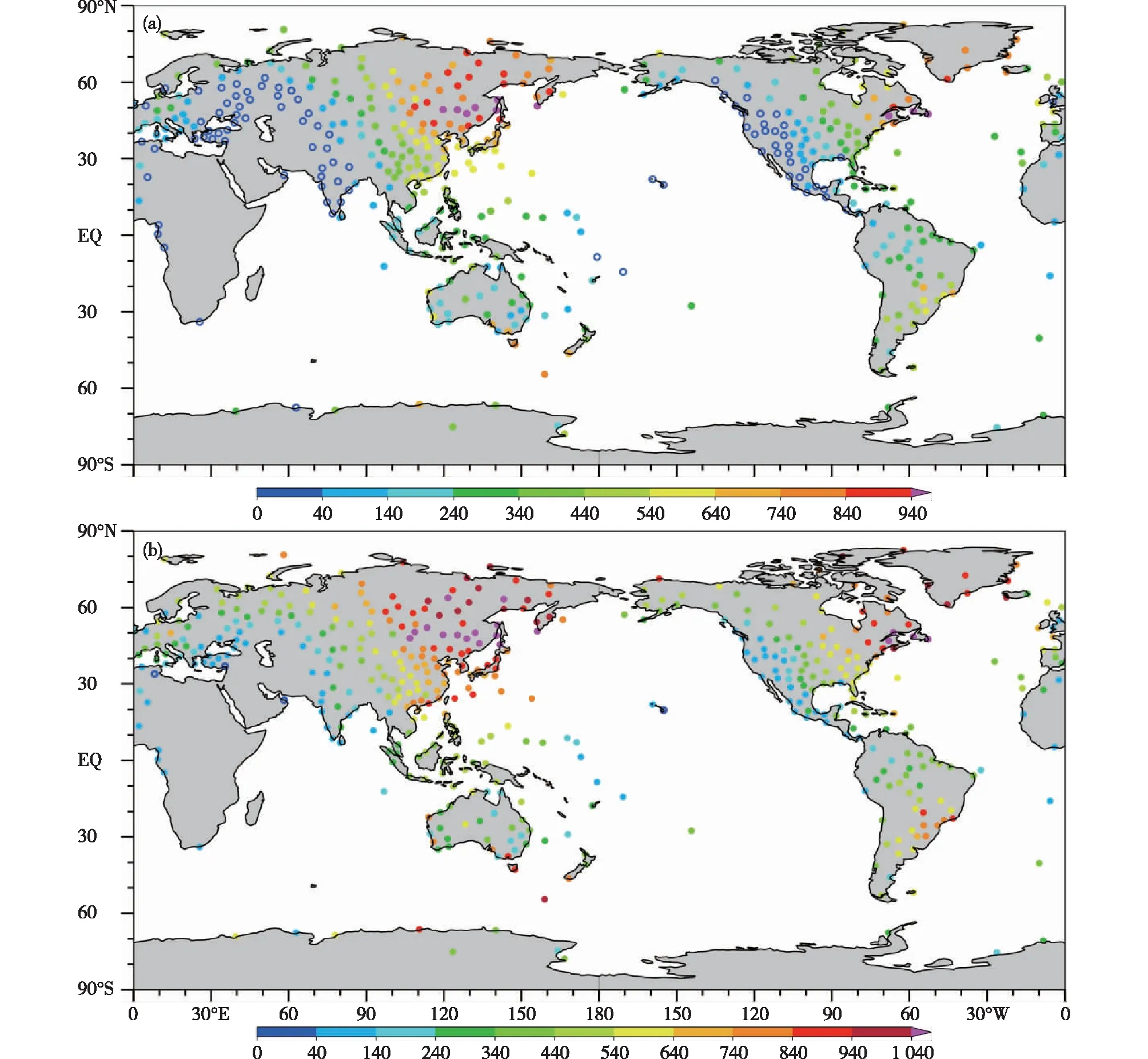
图5 全球筛选出的471个探空站的地理分布,以及这471个探空站点匹配到的2016年1月1日至2020年10月31日(a)MetOp-A卫星的MiRS反演廓线数量和(b)MetOp-A、NOAA-18和NOAA-19三颗卫星的MiRS反演廓线数量,其中空心圈表示匹配到廓线数量小于40根的站点
2 研究方法
在应用“三角帽”法之前,需要对掩星、探空观测资料和MiRS卫星反演产品进行时间和空间上的匹配。由于本研究所使用的5种数据集的垂直分辨率不同(图6),因此首先需要将数据(折射率、温度和水汽压)线性插值到10 hPa等间隔的均匀垂直网格上。由于掩星数据和MiRS反演产品相比其他数据垂直分辨率较高,这可能会引起代表性误差[19],需要对线性插值后的这两种数据进行Savitzky-Golay低通滤波[20]。对高分辨率的数据进行垂直平滑或滤波,有利于去除小尺度波动信息,从而减小与分辨率较低数据之间的代表性误差[20-22]。下面具体介绍数据匹配、质量控制和“三角帽”方法。

图6 MiRS廓线(黑色)、GPS掩星廓线(红色,2016年1月1日12∶27,14.90°N,145.90°E),ERA5数据(蓝色)、探空资料基本层(绿色)和关岛探空站实际探空观测(黄色,2016年1月1日12∶11,13.47°N,144.79°E )相邻两个垂直层之差的垂直分布(单位:hPa)
2.1 数据匹配
本文将观测时间与探空数据的观测时间相差±3 h以内、地理位置在探空数据的空间位置300 km半径内的掩星数据进行匹配;将观测时间与探空数据的观测时间相差±3 h、地理位置在探空数据的空间位置50 km半径内的MiRS反演产品进行匹配。在许多比较GPS掩星和探空观测数据的研究中,大多匹配位于探空观测300 km半径以内的掩星资料[23-25]。考虑到全球探空站点分布不均匀,即在一些地区探空站点的分布过于密集,在全球探空站点密集区域内删除部分站点,以确保余下的探空站300 km半径范围内无其他站点,这样可以避免后续不同站点对同个掩星资料的重复匹配,最终筛选出全球的471个探空站。在空间距离的匹配时,我们使用探空站点的地理位置、掩星廓线的平均经纬度和MiRS反演廓线的平均经纬度。图5b展示了去除重复匹配的廓线后,总共匹配到的掩星廓线数量和水平分布,全球471个探空站匹配到的掩星廓线数量均大于40根。
2.2 质量控制
在计算掩星数据的观测误差标准差之前,本文需要对观测数据,即掩星、探空观测资料和MiRS反演产品进行质量控制,目的是剔除其中的异常数据。基于ZOU, et al[26]提出的顺序质量控制方案(Sequential Quality Control Procedure),本文对掩星、探空观测资料和MiRS反演产品进行范围检查(Range Check)和双权重检查(Biweight Check)。在进行范围检查中,本文剔除那些最高层高度大于50 hPa或者最底层高度小于800 hPa的廓线。然后对通过范围检查的廓线进行双权重检查。具体方法如下:
给定一个有n个观测值的数据集(Xi,i=1, 2, …,n),用数据集的中位数(M)和中位数的绝对偏差(MAD)来确定每个数据的加权系数:
,
(2)
如果|wi|>1,则wi=1,而后用加权系数计算每个数据的双权重均值(而后用加权系数计算每个数据的双权重均值(BM)和双权重标准差(BSD):
(3)
,
(4)
由方程(2)—(4)可以看出,在计算过程中,更接近中位数的数据具有更大的权重,因此,双均值和双权重标准差很少受到极端异常值的影响,这一点优于直接使用样本均值和标准差。最后计算Z分数的值:
,
(5)
将Z分数作为双权重检查的依据,若Z分数大于2.5,即说明数据偏离双权重均值大于2.5倍的双权重标准差,该数据将被剔除。
图7a的实线展示了在进行质量控制不同步骤之后,关岛探空站(13.47°N,144.79°E)匹配到的掩星数据在垂直方向上的数据量变化。质量控制前(虚线)、范围检查后(点划线)和两步质量控制后(实线)掩星数据量的垂直分布表明,许多掩星廓线因探测不到800 hPa以下而被剔除(范围检查),而双权重检测只剔除了少量的资料。图7b展示了掩星数据在质量控制以后折射率的垂直分布,其中红点表示被剔除的数据,可以看到在双权重检测过程中被剔除的数据主要分布在700 hPa以下和300 hPa以上,这与图7a结果一致。
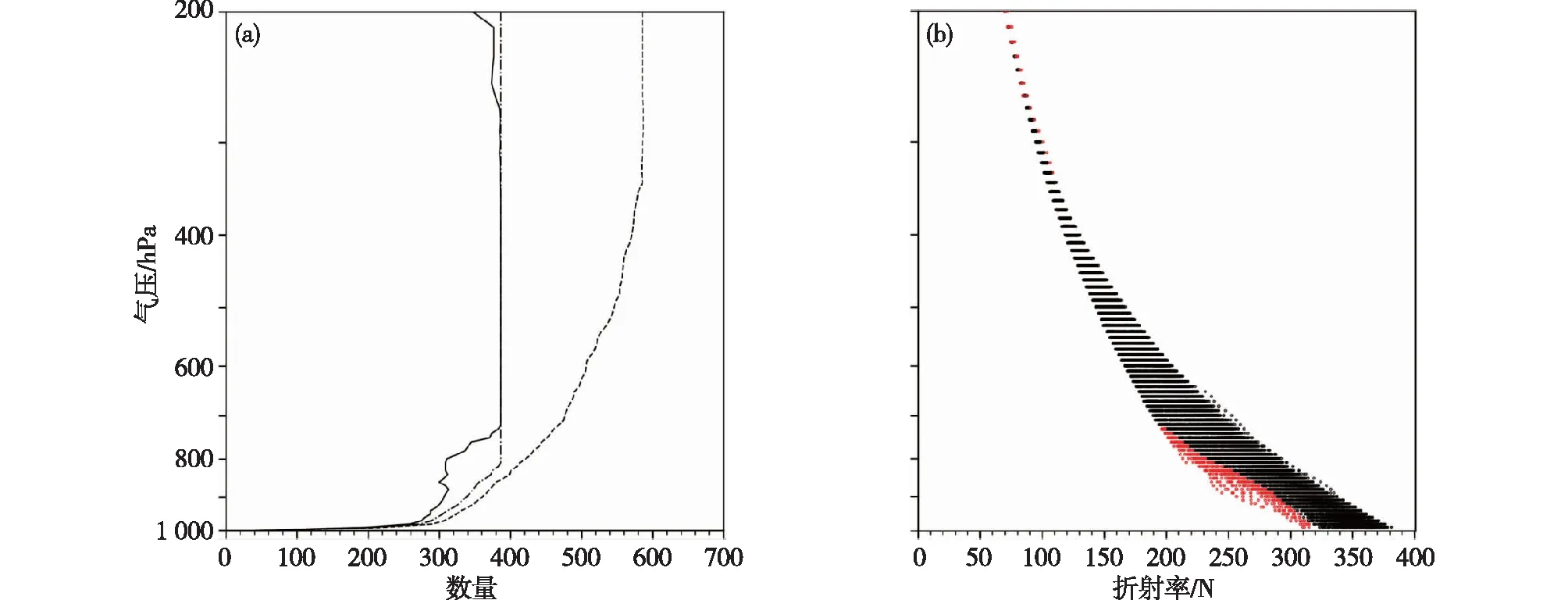
图7 (a)2016年1月1日至2020年10月31日关岛探空观测站(13.47°N,144.79°E)匹配到的质量控制前(虚线)、经过范围检查(点划线)和经过两步质量控制(实线)的GPS掩星廓线数量的垂直分布;(b)经过质量控制的(黑色圆点)和被剔除的(红色圆点)GPS掩星折射率的垂直分布
2.3 “三角帽”法
Grubbs[27]在假设数据集之间没有误差相关性的前提下,第一次推导出“二角帽”法和“三角帽”法的方程。Gray, et al[28]首先用“三角帽”法估计3个振荡器之间的随机误差。Anthes, et al[13]首次将“三角帽”法应用于掩星观测误差的估计,使用掩星、探空观测数据、ERA-Interim再分析和GFS分析资料,估计了掩星折射率、温度和比湿的观测误差标准差。“三角帽”法的主要思路是通过与其他两个数据集的比较来估计某个目标数据集的观测误差,计算简单,且可以考虑并消除数据集之间偏差,只要数据集之间的误差相关性很小,则计算结果就是准确的[15]。接下来简要介绍“三角帽”法的推导。
对于3个数据集A、B和C,希望得到数据集A的观测误差方差,以数据集B和C作为求数据集A的参考数据集。首先计算数据A和B差的方差:
X(A-B)=XA-XB
,
(6)
,
(7)
,
(8)
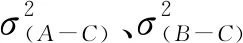
,
(9)
,
(10)
,
(11)
综合方程(9)—(11),得数据集A的误差方差:
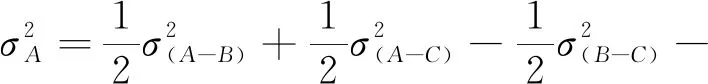
,
(12)
上述方程中σ表示标准差;b表示平均偏差;μ表示平均值。如果忽略方程中偏差项b,则会导致对误差方差的高估[16]。本研究发现,若忽略偏差项b,最后计算的相对误差标准差偏大1%左右。
本研究将探空观测数据、ERA5再分析数据、GFS分析数据和MiRS反演产品进行不同的组合来估算掩星数据的观测误差,假设数据集之间的误差协方差足够小,即与观测误差相比可以忽略不计,利用方程12,用3种不同的资料组合可以得到如下的误差估计公式:
资料组合一:
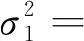
(13a)
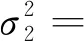
(13b)


(13b)
(13)
资料组合二:
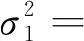
(14a)
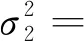
(14b)

(14c)
(14)
资料组合三:
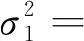
(15a)
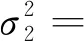
(15b)

(15c)
(15)
在“三角帽”法的估算方程中忽略了不同资料集误差的相关性,即误差协方差项设为0。而实际上不同资料的误差之间存在一定的相关,任何两个数据集中的两个或多个数据集误差的显著相关会使他们的误差估算结果偏低(甚至为负值)[15]。
3 计算结果与分析
3.1 关岛和北京探空站附近的掩星观测误差
在对数据进行归一化处理后,使用方程(13)—(15)用3种不同资料组合来估算掩星观测的相对误差标准差。图8—10展示了经过质量控制后3种资料组合估算的折射率、水汽压和温度相对误差标准差,结果与XU, et al[14]的研究结果相似。其中,经过质量控制的资料计算出的相对误差标准差小于未经质量控制计算出的相对误差标准差,这是因为剔除错误数据可以减少对误差的错误估计。
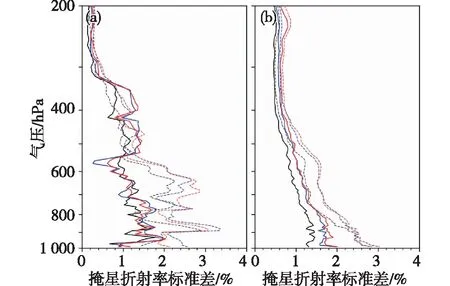
图8 使用资料组合一(RO、RS、ERA5、GFS,黑色),资料组合二(RO、RS、GFS、MiRS,蓝色)和资料组合三RO、RS、ERA5、MiRS,红色)估算的(a)关岛站(13.47°N,144.79°E)和(b)北京站(39.93°S,116.28°E)GPS掩星折射率在质量控制前(虚线)和质量控制后(实线)观测误差标准差的垂直分布
对于掩星折射率观测资料(图8),3种资料组合计算的关岛和北京探空站附近的掩星观测相对误差标准差都随气压的减小而减小。关岛站3种组合估算的结果在所有气压层上都比较接近,从950 hPa的2%减小到200 hPa的约0.1%,而在550至450 hPa,资料组合一(RO、RS、ERA5、GFS)比资料组合二(RO、RS、GFS、MiRS)和资料组合三(RO、RS、ERA5、MiRS)的估算结果小0.2%左右;3种组合估算的北京站附近的掩星观测误差在各个高度上比较统一,都是组合一估算的误差小于组合二、三的结果,而资料组合二、三的结果十分接近,在950 hPa高度,资料组合一(约1.4%)的估算结果比资料组合二、三的估算结果小0.2%左右,随着气压的减小,3种资料组合的估计结果越来越接近,在200 hPa高度最为相近,该处掩星观测的相对误差标准差约为0.4%。
对于掩星1D-Var反演的水汽压资料(图9),3种资料组合计算的关岛和背景探空站附近掩星观测的相对误差标准差都从950 hPa往上从5%开始逐渐增大,在400 hPa达到峰值(约为22%),之后缓慢减小,在200 hPa附近约为13%,且两个站点3种资料组合估算的结果都较为接近,但在500~300 hPa这一高度区间,北京站组合一比组合二、三的估算结果小约5%~10%。
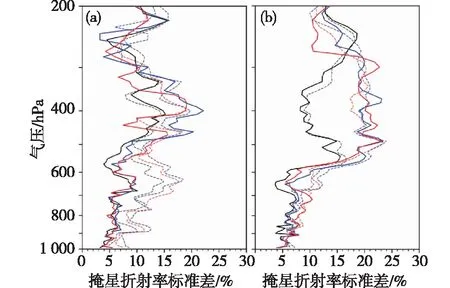
图9 使用资料组合一(RO、RS、ERA5、GFS,黑色),资料组合二(RO、RS、GFS、MiRS,蓝色)和资料组合三(RO、RS、ERA5、MiRS,红色)估算的(a)关岛站(13.47°N,144.79°E)和(b)北京站(39.93°S,116.28°E)GPS掩星水汽压在质量控制前(虚线)和质量控制后(实线)相对误差标准差的垂直分布
对于掩星1D-Var反演的温度资料(图10),关岛站3种资料组合估算的相对误差标准差在950~200 hPa高度都在0.2%左右,但在300~200 hPa高度,资料组合一的结果明显小于资料组合二(小约0.1%),北京站资料组合一估算的相对误差标准差在950~200 hPa高度都在0.4%左右,资料组合二和三的结果在500 hPa高度以下比较接近,在850~500 hPa之间约为0.6%,500 hPa以上资料组合二的估算结果比资料组合三的小约0.1%,在200 hPa高度减小至0.5%左右,资料组合三的估算结果在500 hPa以上始终为0.6%左右。

图10 使用资料组合一(RO、RS、ERA5、GFS,黑色),资料组合二(RO、RS、GFS、MiRS,蓝色)和资料组合三(RO、RS、ERA5、MiRS,红色)估算的(a)关岛站(13.47°N,144.79°E)和(b)北京站(39.93°S,116.28°E)GPS掩星温度在质量控制前(虚线)和质量控制后(实线)相对误差标准差的垂直分布
3.2 全球471个探空站附近掩星折射率和弯角的观测误差
估算掩星弯角观测的相对误差标准差,需要用到探空、ERA5和GFS数据的相对弯角。本研究使用欧洲无线电掩星气象卫星应用机构(ROM SAF)公布的掩星资料处理软件包(Radio Occultation Processing Package,ROPP)[29]中的一维Abel变换模式来计算上述数据的相对弯角值,该软件可从如下网址免费下载:http:∥www.romsaf. org。
本研究将GRAS掩星数据的观测误差估计拓展到全球的471个探空站。图11—13分别展示了3种资料组合估算的全球低、中、高3个纬度带掩星折射率观测的相对误差标准差。3种资料组合计算的掩星折射率观测的相对误差标准差在垂直方向上呈现一致的变化规律,即随气压的减小而减小。在400~950 hPa之间,掩星折射率的相对误差标准差随纬度的增加不断减小,KU, et al[30]利用2001年11月CHAMP掩星数据研究折射率观测误差随纬度的变化、CHEN, et al[11]研究掩星折射率的纬度依赖关系以及XU, et al[14]的研究结果都有类似的规律。而这种低纬度地区掩星折射率观测的相对误差标准差比高纬度地区更大的现象,可能与低纬度地区水汽的汇集和赤道附近的超折射现象有关[31-32]。
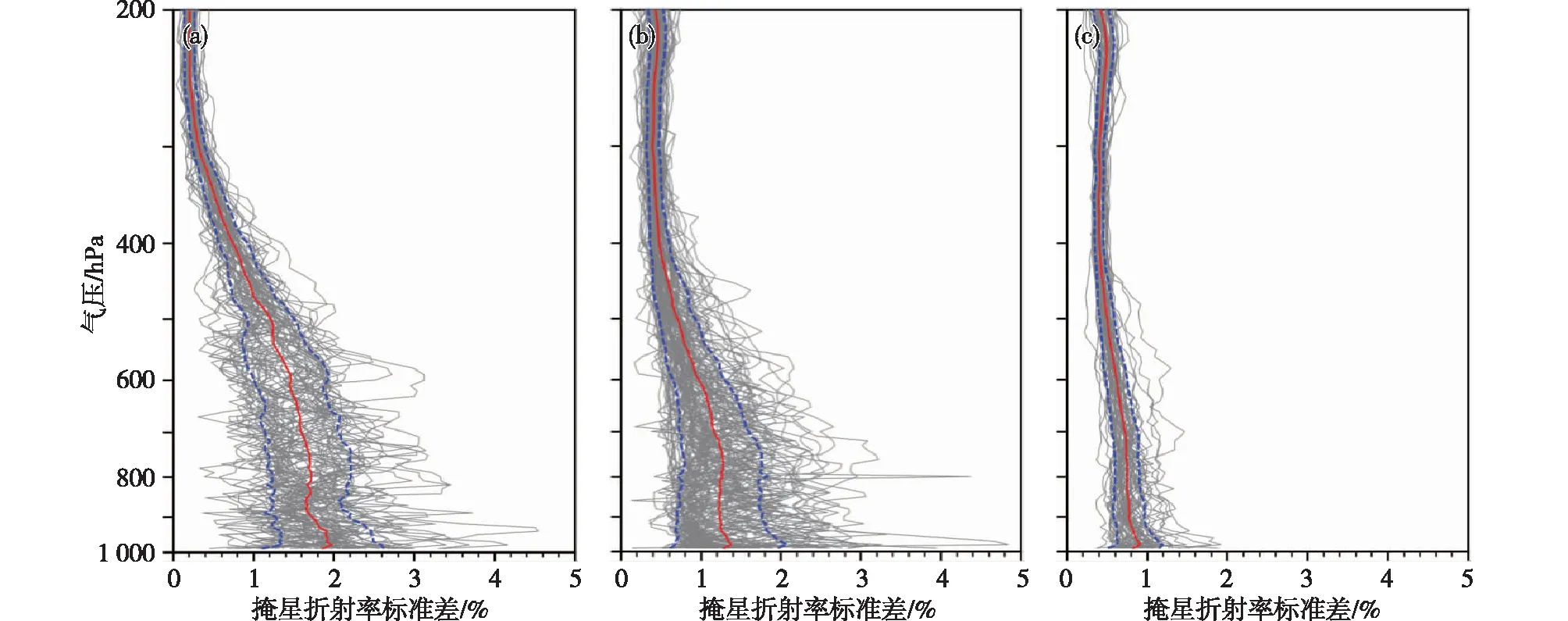
图11 使用资料组合一(RO、RS、ERA5、GFS)估算的(a)低纬(30°S~30°N)、(b)中纬(30°~60°S和30°~60°N)和(c)高纬(60°~90°S和60°~90°N)GPS掩星折射率观测的相对误差标准差(灰色实线)及对应纬度范围内的平均值(红色实线)和标准差(蓝色虚线)

图12 使用资料组合二(RO、RS、GFS、MiRS)估算的(a)低纬(30°S~30°N)、(b)中纬(30°~60°S和30°~60°N)和(c)高纬(60°~90°S和60°~90°N)GPS掩星折射率观测的相对误差标准差(灰色实线)及对应纬度范围内的平均值(红色实线)和标准差(蓝色虚线)
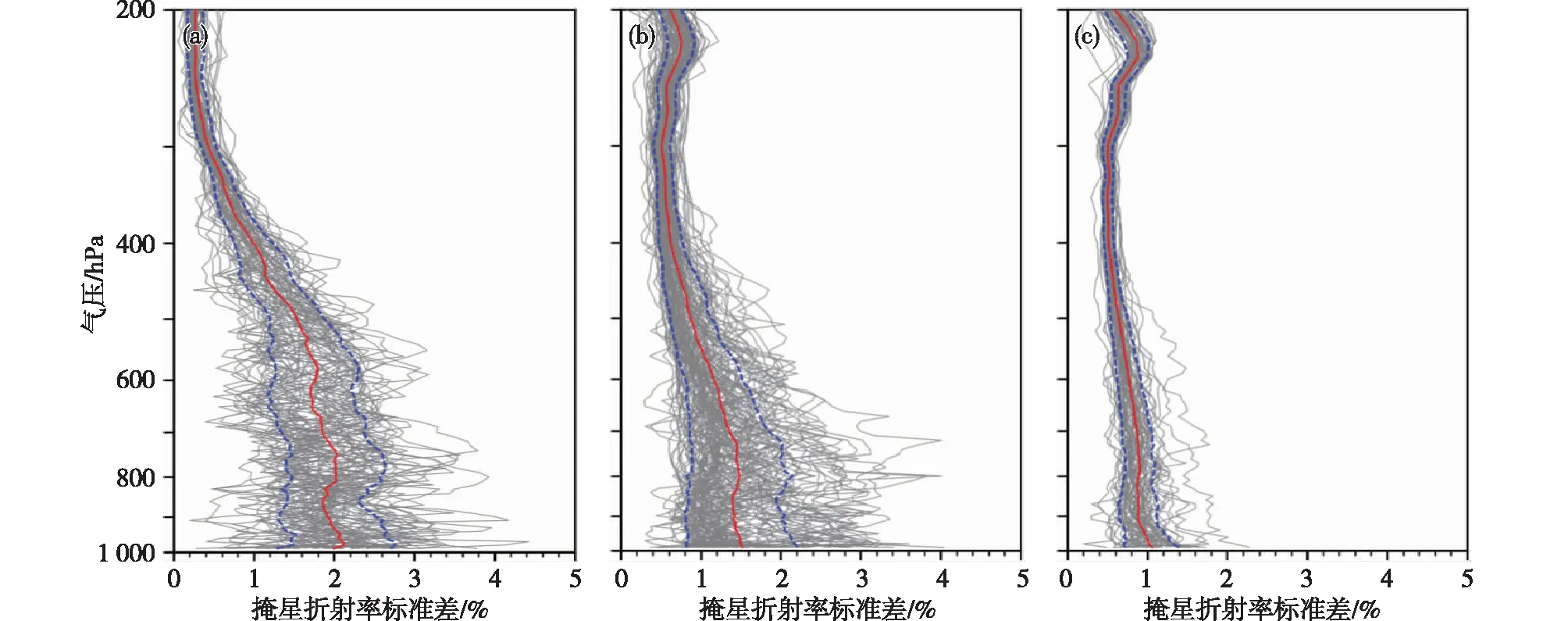
图13 使用资料组合三(RO、RS、ERA5、MiRS)估算的(a)低纬(30°S~30°N)、(b)中纬(30°~60°S和30°~60°N)和(c)高纬(60°~90°S和60°~90°N)GPS掩星折射率观测的相对误差标准差(灰色实线)及对应纬度范围内的平均值(红色实线)和标准差(蓝色虚线)

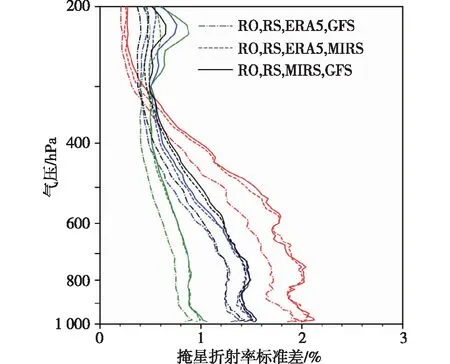
图14 使用资料组合一(点划线)、组合二(虚线)和组合三(实线)估算的全球471个探空站匹配到的GPS掩星折射率的观测误差标准差在低纬(红色,30°S~30°N)、中纬(蓝色,30°~60°S和30°~60°N)、高纬(绿色,60°~90°S和60°~90°N)以及全球范围内(黑色)的均值垂直分布
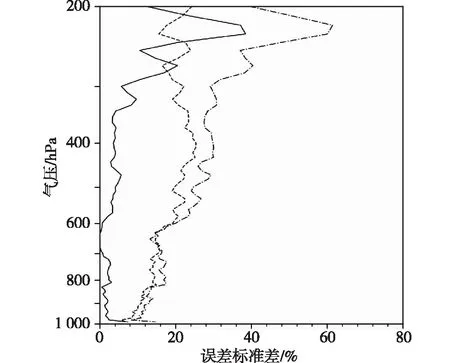
图15 资料组合三相比组合一(点划线)、资料组合二相比组合一(虚线)、资料组合三相比组合二(实线)估算的全球471个探空站匹配到的GPS掩星折射率的观测误差标准差在全球范围内均值的增加百分率(单位:%)
图16展示了使用资料组合二(RO、RS、GFS、MiRS)估算的掩星折射率和弯角观测的相对误差标准差在850 hPa和4 km影响高度上的水平分布(单位:%)。
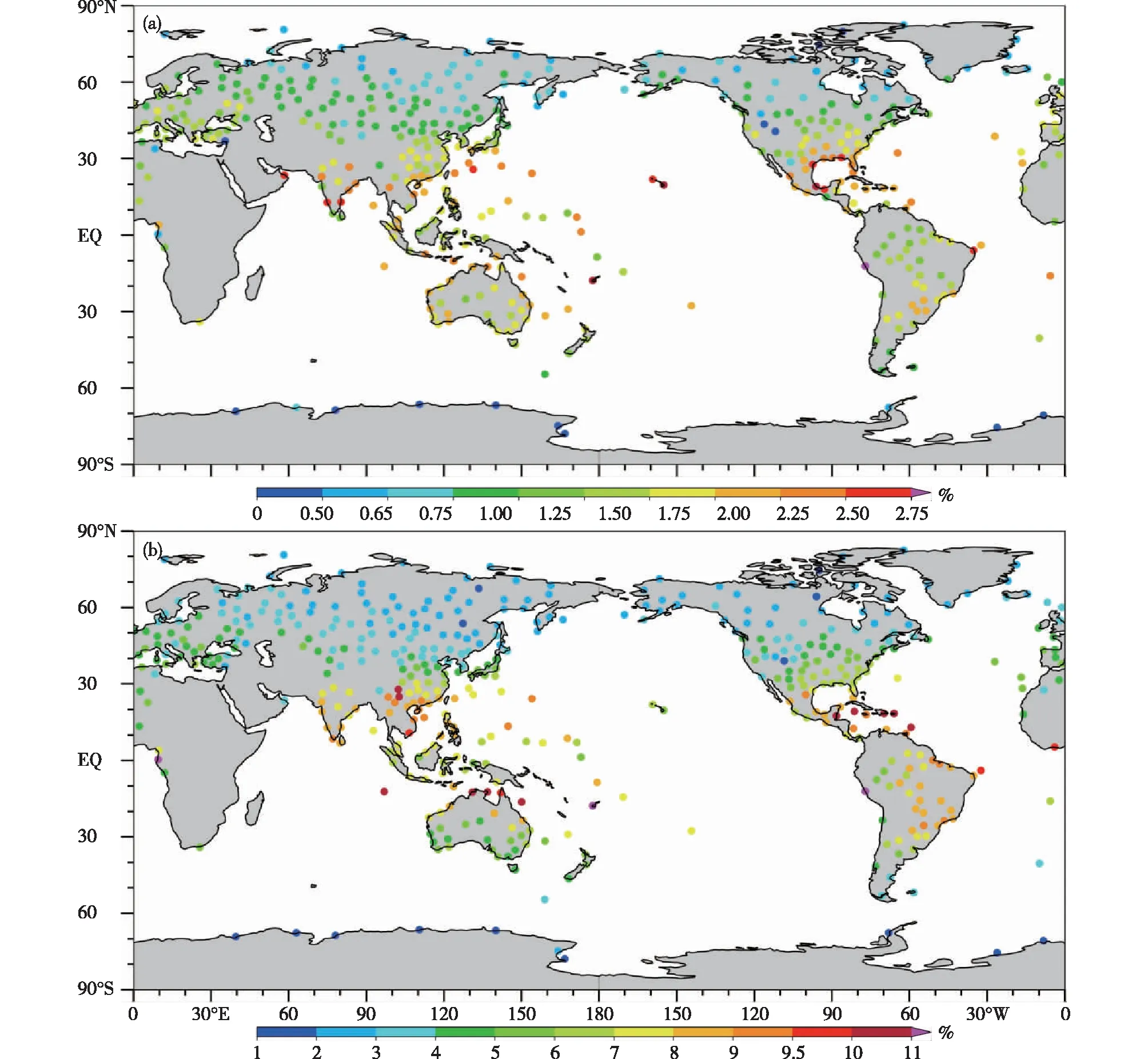
图16 使用资料组合二(RO、RS、GFS、MiRS)估算的GPS掩星(a)折射率和(b)弯角的观测误差标准差在850 hPa和4 km影响高度上的水平分布
随着纬度从低纬度到高纬度,掩星折射率和弯角观测的相对误差标准差不断减小,存在明显的纬度依赖性。资料组合三中使用MiRS卫星反演数据替换了GFS数据,其估算结果与资料组合二估算的结果基本一致。
本文对使用资料组合二(RO、RS、ERA5、MiRS)估算的掩星观测误差结果在每5°纬度带内进行平均,以分析掩星观测误差的垂直经向分布,如图17b、c所示。图17a展示了每5°纬度内的探空站点数,由于35°S和70°N之间每5°的探空站点数多于10个,故图17b、c只展示35°S~70°N的结果。南北半球掩星折射率和弯角观测的相对误差标准差的分布并不完全对称,掩星折射率的相对误差标准差最大值出现在30°N附近,在南北纬30°向两极掩星折射率的相对误差标准差随纬度减小(图17b),弯角观测的相对误差标准差的最大值出现在15°N附近,并由南北纬 15°向两极递减(图17c)。
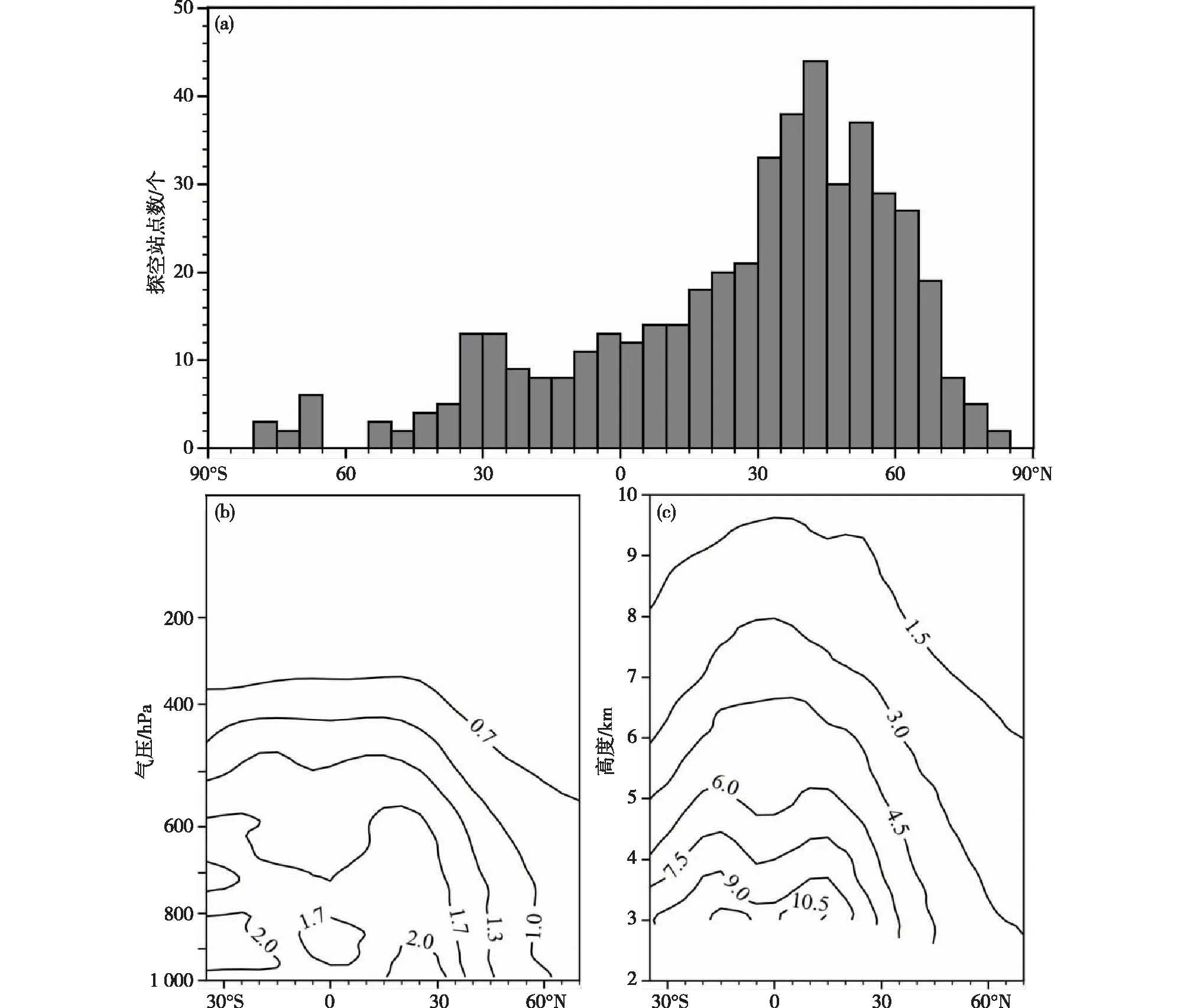
图17 (a)每5°纬度间隔内统计的探空站点数以及每5°纬度范围内使用资料组合二估算的(b)掩星折射率和(c)弯角的平均观测误差的经向垂直分布
4 结论
本研究采用“三角帽”方法,使用掩星、探空观测、ERA5、GFS模式资料以及MiRS卫星微波反演数据这五种资料集的3种不同组合估算掩星折射率和弯角观测的相对误差标准差,估算过程中消除资料集之间偏差的影响,并分析了不同资料组合估算结果的异同。
首先展示了使用2016年1月1日至2020年10月1日的3种资料组合估算的关岛和北京探空站GRAS掩星折射率、水汽压和温度的相对误差标准差,对比两个站点结果表明GRAS掩星折射率观测的相对误差标准差随气压递减。然后使用3种不同资料组合估算了全球471个探空站匹配到的掩星折射率和弯角观测的相对误差标准差,展示并分析了3种资料组合估算的掩星观测误差的全球分布情况。3种资料组合估算的掩星折射率观测的相对误差标准差有相似的纬度依赖性,即在对流层中下层950~400 hPa之间,掩星观测误差随着纬度增大而减小,这与前人研究结果一致。最后分析了3种资料组合估算结果之间的差异。在垂直方向上,资料组合一(RO、RS、ERA5、GFS)的结果始终小于资料组合二和三的结果,这是由于资料组合一中资料集的误差之间存在的相关导致了对误差的低估。随着气压的减小,资料组合一与资料组合二和三估算的结果差异逐渐减小。
与前人研究相比,本研究主要创新点:(1)拓展了使用资料的时间,使用2016年1月1日至2020年10月1日4 a以上的数据;(2)引入MiRS卫星微波反演产品来替换与掩星数据具有较大误差相关性的ERA5数据;(3)计算和分析了全球掩星观测数据的相对误差标准差。
